基于ErlangC公式的座席测算在电力呼叫中心的应用

莫玉纯，吴广财，杨秋勇

（广东电网公司 广东 佛山 528000）

在呼叫中心运营管理中，座席代表作为呼叫中心的生产力，如何对座席代表进行管理是管理工作的重中之重，呼叫中心一般通过服务水平、员工利用率等指标评估利用状况。而排班工作作为贯穿呼叫中心整体工作强度评估、座席代表效率评估等的环节，它既依赖于话务量预测的准确性，更依赖于对座席效能、工作效率的评估。Erlang算法被广泛应用在呼叫中心的研究[1-[2]，尤其是电信行业的客服呼叫中心[3-4]。而对ErlangC算法的应用，没有专门研究涉及电力行业呼叫中心服务。

在电力呼叫中心中，一直以来依赖于“人治”的方式，话务组长等凭经验完成排班计划。在本文，将结合电力行业的实际情况，应用ErlangC公式计算最少座席测算，用于电力呼叫中心的排班管理。

1 座席测算的一般方法

一般而言，座席人员测算主要是基于ErlangC公式的计算方法。它通过响应时长、通话时长、话务强度等预测满足预期接通率水平的最少座席人数，最终形成排班计划。在使用公式时，用户输入预期话务强度、平均通话时长等参数进入ErlangC公式，计算得出在不同服务水平下的最优排班人数。

ErlangC公式：

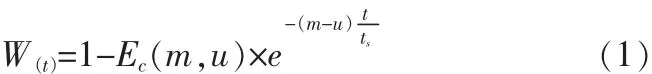
其中：

1）W（t）表示预期的服务水平（即 t秒人工接通率）；

2）t表示响应时长目标（Target Answer Time），即 t秒内接通；

3）ts表示平均通话时长（Average Call Duration），单位秒；

4）m表示预期的座席人员数；

5）u示话务强度（Traffic Intersify），即每 1秒内需要的工作量/话务量；可由计算公式：

表示，其中Y表示T时间长度内预期的话务量，T表示时间长度，单位秒；

即u为每秒话务量；

6）Ec（m，u）表示呼叫等待概率，即每通来电呼入时，由于座席忙而无法接听的概率，由计算公式：

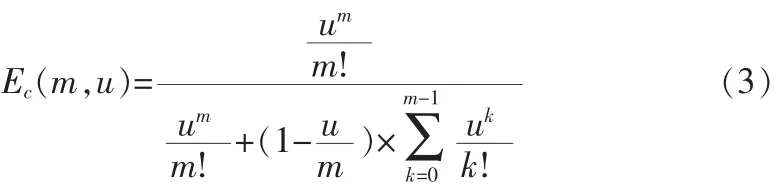
表示。

由于ErlangC公式是由Poisson方程推导而来，而Poisson方程的概率分布函数为：

因此可利用Poisson方程的概率密度函数计算呼叫等待概率 Ec（m，u）。

将公式（2）、（3）代入公式（1），输入相应的参数，不断迭代m=1，2，……，即可得到每增加一名座席时的服务水平W（t）的分布，最终可知预期服务水平下所需的最少座席人员数量。

然而ErlangC公式在决定座席数量的同时，也暴露出它本身的缺陷。文中将ErlangC公式和呼损率、每名座席的服务水平相结合后，修正ErlangC公式的缺陷，最终应用到电力呼叫中心的实际运营管理当中。

2 利用修正的ErlangC公式进行座席测算

ErlangC公式本身的缺陷是其具体的假设条件导致的。这些假设条件基于理想状态或数学推理的考虑提出，实际工作中难以完全满足。因此，为了使ErlangC公式能够更贴合实际工作，需要对假设条件做相应的修正调整。

ErlangC公式假设条件有：

1）假定话务量在定义的时间段内是较为平稳；

2）假定座席人员是可以无上限增加的；

3）假定当呼入通话不会被客户主动挂机，而是永不放弃地进入等待队列中的。

对ErlangC公式的修正调整有：

2.1 话务量的修正与调整

ErlangC中假定话务量Y是较平稳的，然而实际上话务量在不同时间粒度下存在剧烈波动（见图1），因此简单地假定话务量在任意时间段平稳是不合理的。

修正方法：

1）降低时间段的粒度，可有效地满足“平稳且均匀分布”的假设条件。在应用中采用每小时段或每半小时段的时间粒度；

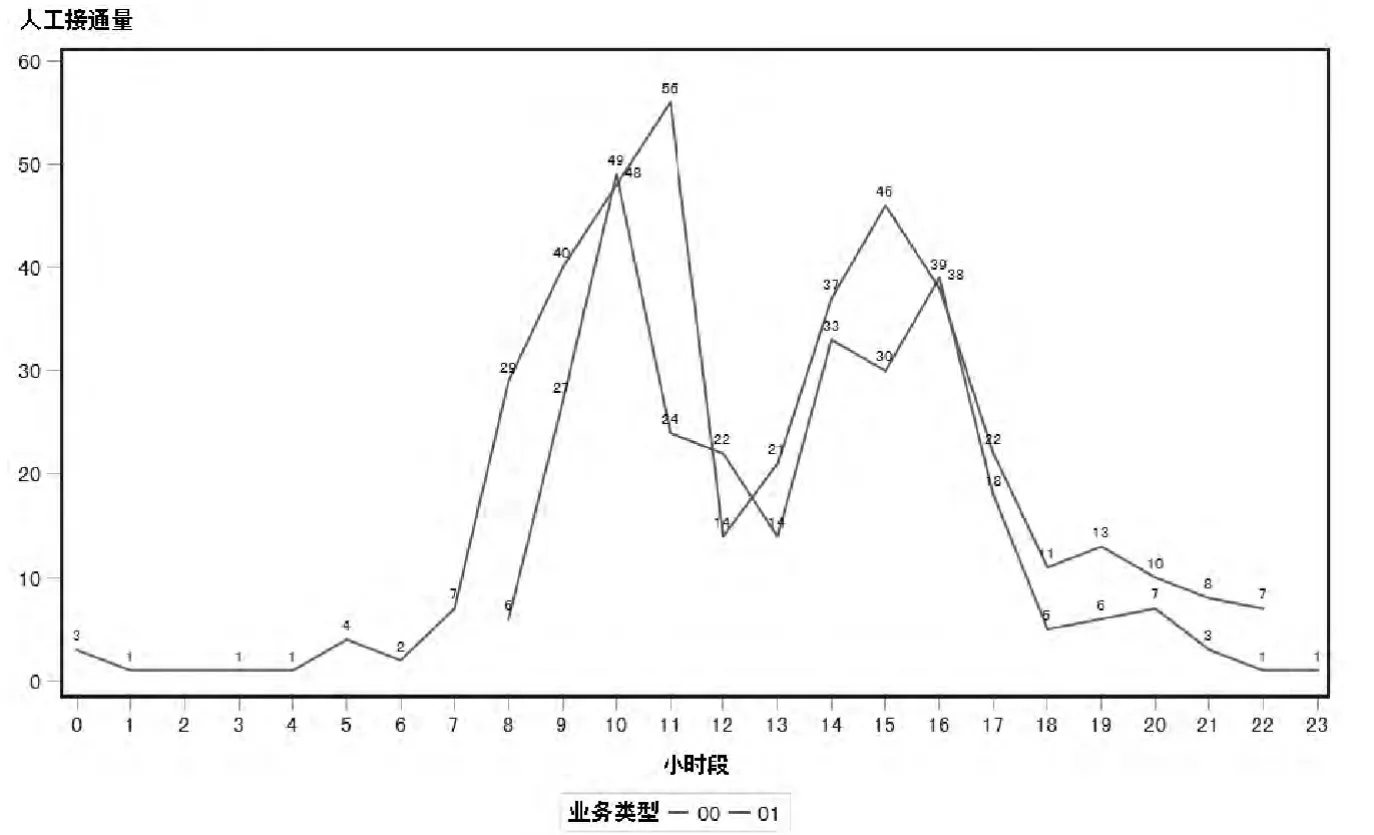
图1 某日不同小时段的话务量变化Fig.1 Call traffice in hours

2）预测的话务量引入呼损概念，应用公式5对预测话务量做调整：

其中，pl表示呼损率。

2.2 平均通话时长的修正与调整

一般而言，ErlangC公式中的平均通话时长是不区分不同类型的呼入通话存在较大差异的（见表1）。然而在实际工作中，尤其是电力行业，不同业务类型的呼入通话的通话时长存在极大差异，简单地将所有呼入采用统一的平均通话时长是不合适的。

应用SAS软件提供的T检验方法验证，结果如图2所示。

显然，方差齐性检验的P值<0.000 1，表示方差不等；采用Scatterthwaite方法的 T检验，其 P值为 0.15，在 95%的置信水平下，拒绝了“均值相等”的原假设。

图2 SAS软件PROC TTEST结果Fig.2 Output of SASProc TTEST

表1 不同业务类型的平均通话时长Tab.1 The average call duration different business types

因此需对平均通话水平t′s进行修正，其方法是利用公式：

其中，

1）Yi表示第i类呼入通话的数量；

2）tsi表示第i类呼入通话的平均通话时长；

3）j表示共有j类不同类型的呼入通话。

因此，话务强度u修正调整为：

2.3 呼叫等待概率的修正与调整

ErlangC公式中假定客户永远不会主动挂机，然而在电力呼叫中心中，客户存在普遍性的耐心不足，因此需要引入呼损率对呼叫等待概率做修正（见表2）。

表2 不同业务类型话务量的呼损率Tab.2 Call loss rate traffic of different service types

修正方法：对于已呼损的呼入通话而言，其呼叫等待概率为1，占全体的百分比为呼损率。因此，应用公式（8）对公式（3）做调整：

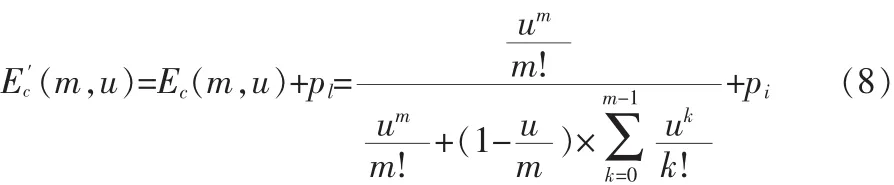
其中，pl表示呼损率。

综合公式（1）～（8），得出最终应用公式（9）：

3 实例研究

在某95598客服中心的运营中，选取某一日的每小时段数据（见图3），其实验步骤如下：

1）选取时间粒度为小时的话务量数据，并将该时段话务量缺失的设定为0；

2）定义初始值：t=20秒接通；时间段为1小时，即3 600秒；预期服务水平为85%，即要求20秒接通率至少为85%；设定最大座席数量为10；

3）计算相关参数：

①平均通话时长：（各类型话务量×该类平均通话时长）/总话务量；

②话务强度：应用公式（7）计算话务强度；

③应用公式（8）及SAS软件pdf（）函数计算呼叫等待概率；

4）应用公式（9），循环迭代计算不同座席数量下的服务水平；

5）仅保留超过指定服务水平（85%）的最小座席数量。

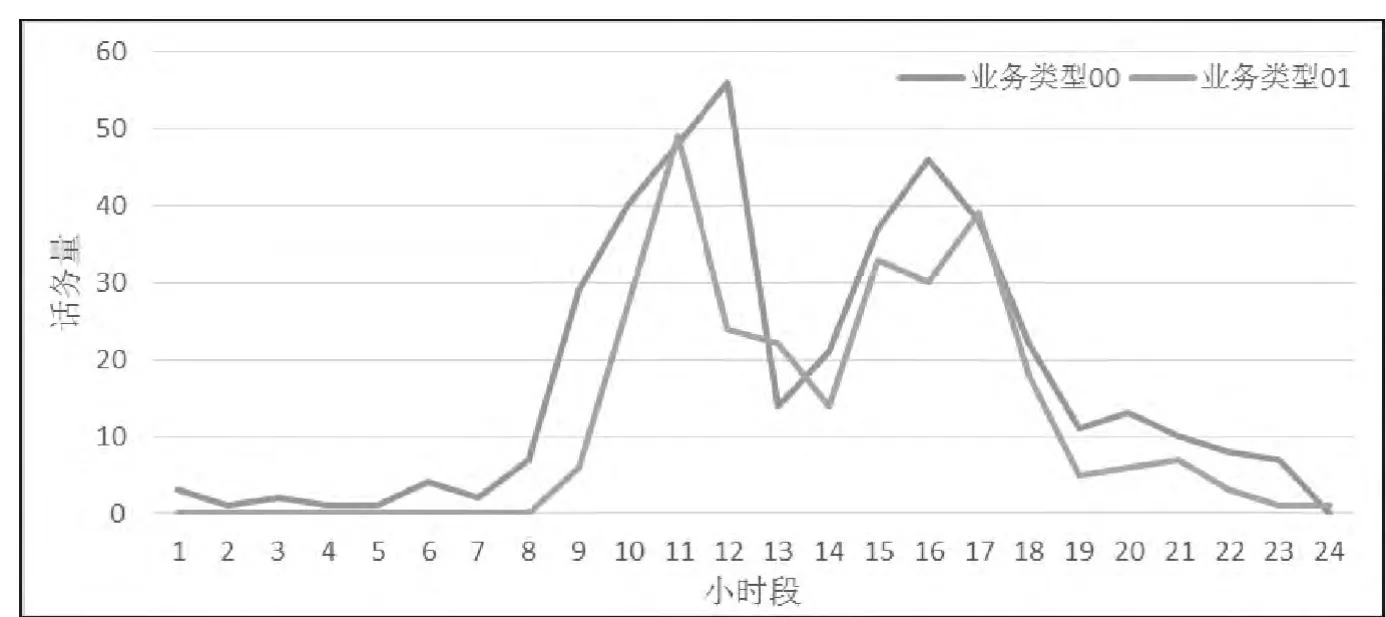
图3 不同业务类型在各时段的话务量Fig.3 Call Tracfic in different hour and different type

最终得出下述结果图4所示。

从表2及图3可以看出，在不同小时段设置的最少座席数量相差较大。在实际排班工作中，需要做适当的调整：

1）在上午阶段，可设置8～9名座席；中午休息阶段可轮班小休；下午继续9名座席的安排；

2）到晚上阶段，应设置3名座席以保证服务水平；

3）而在深夜及凌晨时段设置2名座席即可能满足服务水平要求。

4 结 论

本次研究提出利用ErlangC公式对电力呼叫中心的人员安排进行预测，其中根据电力行业的呼叫中心的特性进行积极的修正，使之符合业务逻辑和实际情况，预测结果也比较准确。但在此研究中，尚未考虑座席工作时段的连续性、座席在应对不同类型的呼入通话时工作能力的不同等对测算的影响。后续的工作与研究中，将结合最小方差管理等方法评估座席人员在不同时段、不同业务类型的工作能力，从而达到最大化地利用座席人员的优势和能力。

图4 各时段满足超过指定服务水平（85%人工接通率）的最少座席数量Fig.4 Minimum agent in 85%service level

[1]戚艳军，徐光辉，李强.Erlang算法在呼叫中心的应用研究[J].计算机技术与发展，2010（6）:179-182，187.QI Yan-jun，XU Guang-hui，LI Qiang.Erlang algorithm applied research in the call center[J].Computer Technology and Development，2010（6）:179-182，187.

[2]王明.呼叫中心系统中排班算法的设计与实现 [D].北京：北京交通大学，2008.

[3]苏晓东，梁艳.多业务呼叫中心系统座席分配问题研究[J].信息技术，2010（8）：12-15.SU Xiao-dong，LIANG Yan.Research allocation system multiservice call center agents[J].Information Technology，2010（8）：12-15.

[4]朱红芳.呼叫中心排班人员数目决策的实证研究 [D].天津：天津大学，2006.

[5]张云帆，徐雅斌.基于CTI技术的呼叫中心设计与实现[J].辽宁工学院学报，2006（1）：7-9.ZHANG Yun-fan，XU Ya-bin.CTI call center technology，Design and Implementation[J].Liaoning Institute of Technology，2006（1）:7-9.

[6]谢传柳，王俊峰，夏正洪，等.大型呼叫中心排班算法的研究[J].计算机工程与设计，2010（23）：5108-5112.XIE Chuan-liu，WANG Jun-feng，XIA Zheng-hong，et al.Research large call center scheduling algorithm[J].Computer Engineering and Design，2010（23）:5108-5112.