双污染源对室内浓度场分布影响的数值模拟研究

王 怡，刘 波，曹莹雪，杨 洋

（西安建筑科技大学环境与市政工程学院，陕西 西安 710055）

在工业生产过程中会产生大量的有毒有害污染物，其中包括气体、固体悬浮颗粒和粉尘等．这些物质无论是排放到大气中还是滞留在室内，不仅对周围环境造成极大的破坏，还会严重威胁到人的身心健康[1]．因此如何控制工业有害物的排放和对环境的影响是当前亟需解决的问题．

为了解决此问题，许多国内外学者运用数值模拟和实验研究的手段分析了室内存在单一污染源时，污染物在室内的分布情况[2-4],并在此基础上分析了影响室内污染物浓度分布的多种因素．对于分析室内房间的气流流动和污染物浓度分布，Brohus和 Nielsen[5]教授做了大量的有关于置换通风的实验和CFD数值模拟研究．H.Lee等[6]运用实验和数值模拟手段，研究了不同污染源位置对室内污染物浓度分布的影响．A.Duci，K. Papakonstantinou[7]通过数值模拟方法对大空间室内污染物分布进行了研究，结果得出选择合理的机械通风方式可以有效降低室内污染物浓度．Baoqing Deng[8]运用数值模拟手段研究了不同通风方式下对室内地毯有机化合物排放的影响．孙斌[9]通过改变室内污染源的位置，运用CFD软件模拟研究了在三种通风方式下办公室内的苯污染物浓度分布规律，比较得出在三种通风方式下最佳的污染源位置，并总结出不同的污染源位置对室内污染物浓度分布影响不同．

目前，国内外对室内污染物浓度分布的分析多基于民用建筑，但实际的工业建筑中往往存在多个工艺设备同时作业的现象，而现有研究多针对室内仅存在单一污染源的情况进行分析，对于建筑内部多存在多污染源的情况时，设计人员进行设计估算时可能只是把单一污染源散发的浓度进行简单的叠加，并没有考虑多污染源共同作用对室内污染物浓度分布的影响，对于室内环境影响的评价,也存在这方面问题,这样会影响评价的准确性．因此，研究多污染源共同作用下室内污染物的分布情况显得尤为必要．

运用数值模拟手段，对比分析了单污染源单独散发污染物浓度场的数值叠加值与双污染源共同作用浓度场之间的差异，并在此基础上改变污染源散发强度，分析总结源项浓度对此差异的影响．

1 工业厂房污染物分布数值模拟方法及验证

1.1 数学模型

房间的模拟属于三维稳态模拟，数值模拟将采用k-ε模型，组分传输模型模拟浓度分布．本文采用有限容积法作为控制方程的数值模拟解法，综合考虑网格的划分和计算精度的要求，求解时选取二阶迎风格式，并选取SIMPLE迭代算法作为本文数值模拟中的压力速度耦合项[10]，动量方程和湍流量方程均采用二阶迎风格式．

根据质量守恒定律，建立的空间污染物输运方程如下[11]ux， uy， uz为空间内任一点在x、y、z三个方向上时均速度分量;Γ为空间任一点污染物扩散系数；s( x, y, z)为源项，即任意一点的污染物的释放强度．连续性方程

动量方程

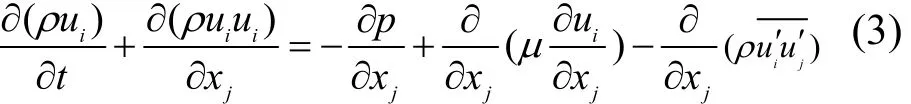
k方程为

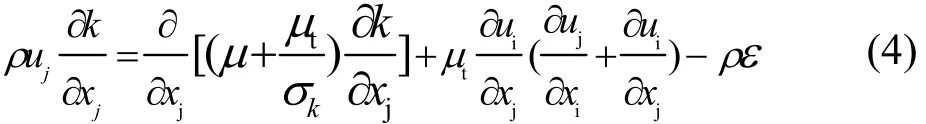
耗散率ε微分方程为

求解由方程(1)，（2），(3)，(4)和(5)构成的微分方程组，就可求出空间的污染物浓度分布[12]．

1.2 模型验证

通过与前人实验[13]结果进行对比分析，来验证数值计算的准确性．采用与实验一致的物理模型：实验通风系统为吹吸式通风，在工作台上放置一个均匀散发酒精的装置，散发速率为4.2m/s，吹风口尺寸为1 m（宽）×0.5 m（高），吹风口尺寸为0.9m（宽）×1m（高），见图（1）．在工作台上有两个监测点，在吹风口上端有三个监测点，图2显示当吹风口速度为0.41m/s，吸风口速度为0.37m/s时，五个点的酒精浓度．由图2可知，数值模拟的结果和实验数据的平均误差为22%,具有较好的吻合性．

图1 实验室平面图(来自于文献13)Fig.1 Laboratory plan (from literature 13)

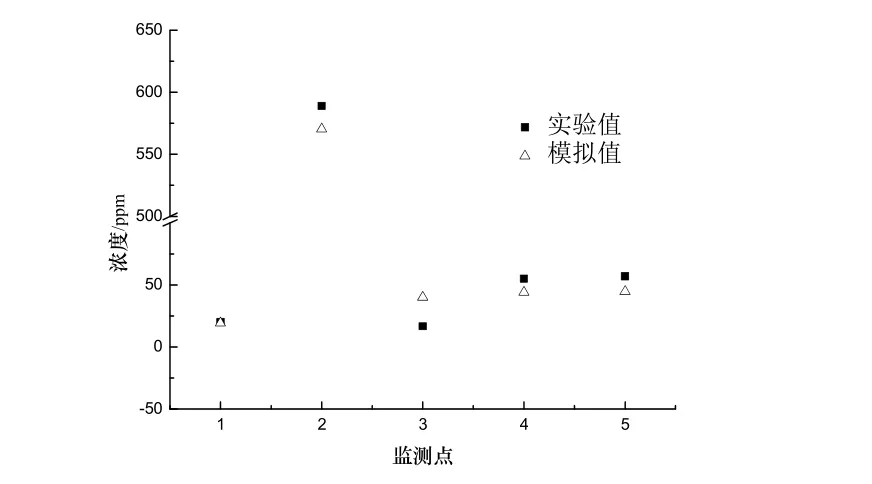
图 2数值模拟的有效性验证Fig.2 Validation of numerical simulation

1.3 物理模型建立

由于在工业建筑中空间非常高大，污染源的源相强度也非常大，因此我们采用数值模拟方法对一个工业建筑中的双污染源的情况进行研究．

建立的模型为某工业厂房，尺寸为长*宽*高=10 m×10 m×8 m，在本模拟中认为室内空气属于连续性介质，并且为不可压缩气体，室内温度设置为300 K，房间中部有两个体积为1 m×1 m×0.8 m的污染源，分别为污染源 1和污染源 2（图 3），选取N2O为示踪气体进行研究．污染源选取质量流量边界条件，室内窗户为压力边界条件，墙壁壁面与屋顶等作为绝热边界条件处理．经过浓度场分析选取污染源2四周具有代表性的四个点（图4），A(6.5，6.7，Z), B(6.5，5.2,Z)，C(5，5.2，Z)，D(8，5.2，Z)为典型点，研究沿房间高度上污染物浓度的变化，从而分析室内浓度场的变化规律．由于网格的疏密程度对数值模拟计算的结果具有较大的影响，因此验证网格无关性显得尤为重要，本文对污染源同时散发的情况分别采用250万、200万、150万、80万、50万和20万六种不同的网格数量进行数值计算，以来确定适用于本文的网格数量，同时更进一步说明数值模拟的准确性．考虑数值模拟的计算准确性与计算周期问题，经过网格无关性验证，本模拟选取的网格数量为80万．

图3 物理模型Fig.3 Physical model

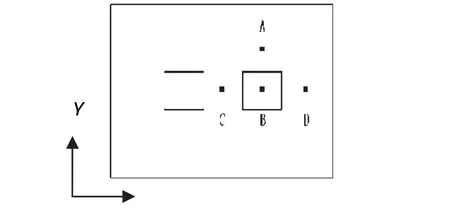
图4 典型点位置示意图Fig.4 Schematic diagram of the typical points position

2 工业厂房中双污染源数值模拟的分析

为了对比分析单污染源数值叠加场与多污染源共同作用下室内浓度场之间的差异，本文分别模拟了单独开启污染源1、单独开启污染源2和同时开启污染源 1、2的工况，工况说明见表 1,并定义了叠加差δ的概念．叠加差的计算公式如下：

式（6）中：δ为叠加差，单位kg/m3;1C为单独开启污染源1和单独开启污染源2时在任一点处污染物浓度值的数值叠加值,单位kg/m3；2C 为污染源1和2同时散发时的浓度值,单位kg/m3．

同时为了进一步分析污染源散发量对此数值叠加和共同作用间差异的影响，本文亦将污染源散发量由0.01 kg/s延伸至0.1 kg/s，工况说明同见表1．

由于污染源1和污染源2的位置不同，所以相同点处的浓度值存在一定的差异,由于 B点处于污染源2的正上方，所以B点在污染源2单独散发时的浓度整体要高于污染源1单独散发时的浓度．而由污染源1和污染源2单独散发时数值叠加值和共同作用的浓度图可以清晰地看出数值叠加浓度值整体要高于共同作用的浓度值，这说明单污染源数值叠加和多污染源共同作用之间存在明显差异，在设计计算时不能将其进行简单的叠加，否则将会造成结果的偏差．

为了具体分析各点的差异，分别比较了四个点的单污染源单独散发时数值叠加值与双污染源共同作用值，并计算了各点的叠加差值，见图6和图

7．从图6和7均可看出数值叠加值1C整体要高于共同作用值2C，这是由于扩散速度与浓度差有关．只要在一个混合物中存在浓度差，必定会发生传质．传质是混合物中因组分的浓度差而引起的质量传递，浓度梯度提供了这个组分的驱动势[14]．随着浓度差增大，扩散速度增大，浓度差减小时，扩散速度也随之减小．双污染源存在时其浓度值高于单污染源存在的情况，其扩散速度要大于单污染源存在的工况，所以共同作用的实际浓度C2是高于两个污染源单独存在时的叠加值C1．

表1 30种工况下污染源散发情况Tab.1 Pollution sources distribution under 30 conditions

由图 6可知，两条曲线的变化趋势是一致的，在2 m以上的工作区范围之外，四点的浓度趋于接近，说明在工作区以外，浓度基本保持不变．在2 m以下的工作区范围之内浓度变化剧烈，浓度值相比于整体略大．从图中可知，B点在此区域的浓度值要明显高于其他三点，这是由于B点处于源相的正上方，浓度值最大，而C点在工作区范围之内相比于A和D两点浓度值略大这是由于两污染源共同作用使得在两污染源之间浓度值较大．

由图7可知B点的1-3 m处的叠加差值与其他三点有较大的差异，可以看出随着高度的增加B点的叠加差值逐渐减小，甚至出现了负值，之后逐渐增大，最终趋于稳定．这是由于B点处于射流的中轴线上，具有较大的浓度梯度，叠加差逐渐减小并出现了负值这是由于边界效应[15]的存在导致的，由于污染源1和污染源2都存在各自的边界，并且边界之间存在着一定的相互作用．当两污染源同时散发时，对对方的浓度扩散起到阻碍作用，使得污染物被阻挡在了源项的上方，即污染源1的存在阻碍了污染源2散发的污染物越过其并向另一侧扩散的趋势，同时由污染源1处的上升气流将此部分污染物携带并送至出口处，因而此处的共同作用时污染物浓度值随着高度的增加逐渐大于单污染源单独散发时的浓度数值叠加值，虽然在此区域随着高度的增加射流不断卷席周围的空气，使得B点处的浓度不断减小，但是由于边界效应的存在，使得在此区域共同作用时的污染物浓度相对单污染源单独散发时的浓度逐渐增大．而超过 1.72 m这一区域时，射流逐渐进入末端区，这是一个迅速扩散的区域，在这个区域中，射流开始趋同于周围的空气，卷吸作用减小，射流速度也逐渐减小[16]，浓度趋于平缓，叠加差值也将保持不变．

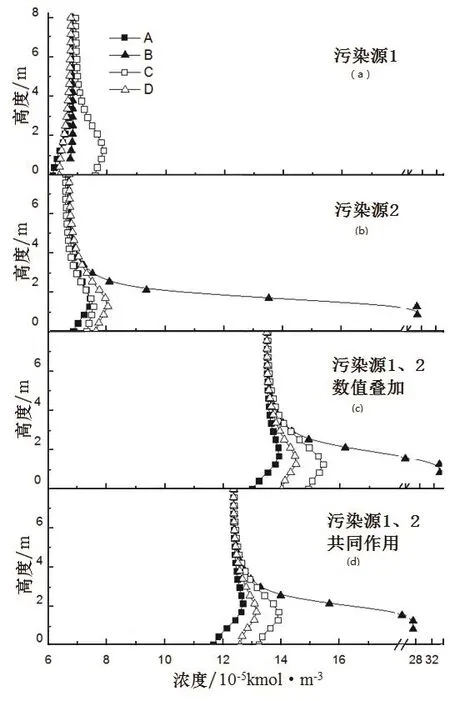
图5 不同工况下四点的浓度分布Fig.5 The concentration distribution of four points under different conditions

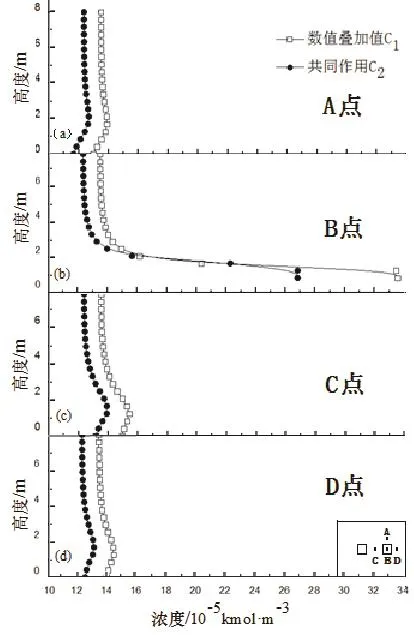
图6 数值叠加值与共同作用值在四点的对比Fig.6 Superposition value and emitting simultaneously in the four points

由图5和图6可以看出，在case1-3中各点污染物浓度峰值均出现在1.72 m处，故图8给出了Z=1.72 m处平面上的等叠加差曲线．从图中可以看出只有在两个源项正上方的叠加差值小于零，而其他各点的叠加差值较均匀，同时证明了选取的四个典型点具有代表性，认为其流场的变化规律可以代表整个流场的变化规律．

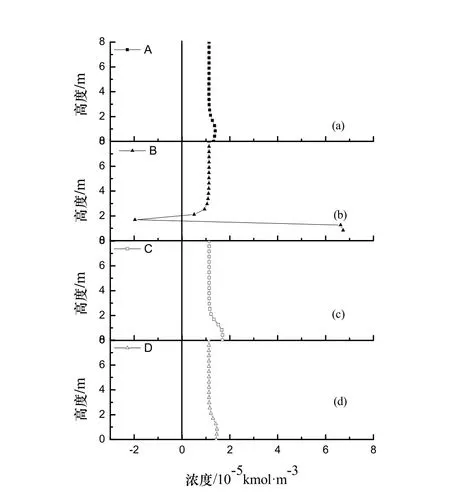
图7 四点的叠加差值Fig.7 Superposition difference of the four points the four points

图8 Z=1.72m处等叠加差曲线图（10-5 kmol·m-3）Fig.8 Superposition difference distribution figure inZ=1.72m

2.2 源项污染物浓度对数值叠加浓度场与共同作用浓度场间差异的影响

为了分析源项浓度对单污染源数值叠加浓度场与双污染源共同作用浓度场之间的差异，文中通过改变污染源散发浓度，从0.01-0.10 kg/s（见表1）均匀变化，并计算A、B、C、D四点的叠加差平均值，对比叠加差值的变化，以此来分析源项浓度对此差异的影响，结果如图9所示．

从图中可以看出随着浓度的增大，叠加差不断增大，这是由于源项浓度的增大使得多污染源相比于单污染源单独散发时浓度扩散速率加快，因此叠加差值逐渐增大，这说明随着浓度越大，多污染源的数值叠加值与共同作用值的差异越加明显，此时不能将污染源浓度进行简单叠加，而是要考虑污染源之间的相互作用．如果不考虑污染源之间的相互作用，在设计计算时，计算的浓度值偏大将会导致能耗偏高．在时间不充裕的情况下，在设计计算时可对多污染源的浓度场进行简单的估算，本文将污染源浓度与叠加差值进行线性拟合，得到公式如下：

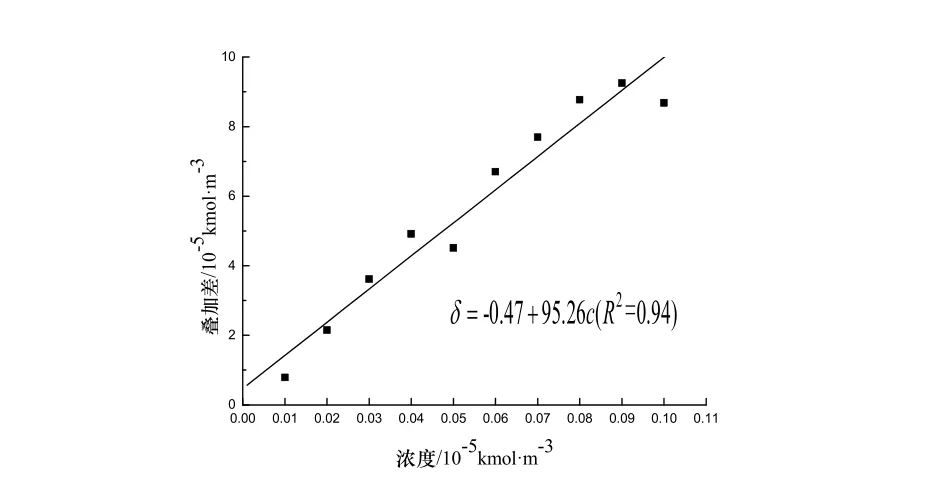
图9 浓度不同时叠加差的变化规律Fig.9 the changes of the superposition difference in different concentration

目前公式的应用范围是源项浓度在 0.01～0.10 kg/s，后续的讨论中会逐渐扩大应用范围，为通过单污染源估算双污染源浓度场提出一个合理的方法．

3 结论

通过数值模拟手段，对比分析了单污染源单独散发污染物浓度场的数值叠加值与双污染源共同作用浓度场之间的差异，得到如下结论：

(1)定义了叠加差δ的概念，叠加差δ越大，说明单污染源单独散发数值叠加值与双污染源共同作用值的差异越大．

(2)分析了单污染源单独散发和双污染源共同散发时在四点的浓度分布，发现了在整体上单污染源单独散发数值叠加值要大于双污染源共同作用值；而在源项上方，由于射流作用和边界效应的存在，使得B点的叠加差先减小后增大，最后趋于稳定．

(3)通过改变源项浓度，发现了叠加差与源项浓度呈线性变化，并进行线性拟合，得到公式如下：

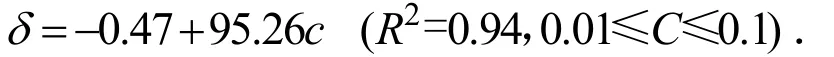
References

[1] 孙一坚. 工业通风[M]. 北京:中国建筑工业出版社,1994.SUN Yijian. Industrial Ventilation [M]. Beijing: China Architecture & Building Press, 1994.

[2] 刘威.室内污染物浓度分布的数值研究[D].广州:广州大学,2006.LIU Wei. Numerical simulation of air contamination dispersal in a room [D]. Guangzhou: Guangzhou University,2006.

[3] XING H, HAT ton A, AWBI HB. A study of the air quality in the breathing zone in a room with displacement ventilation. Building and Environment, 2001,36(7):809-820.

[4] ATILA Novoselac. Development of new and validation of existing convection correlations for rooms with displacement ventilation systems [J].Energy and Buildings, 2006,38: 163–173.

[5] Brohus H, Nielsen P. Personal exposure in displacement ventilated rooms [J]. Indoor Air, 1996,6(3): 157-167.

[6] LEE H, AWBI H.B. Effect of internal partitioning on indoor air quality of rooms with mixing ventilation-basic study[J]. Building and Environment, 2004,39:127–141.

[7] DUCI A, PAPAKONSTANTINOU K, CHALOULAKOU A. Numerical approach of carbon monoxide concentration dispersion in an enclosed garage[J]. Building and Environment, 2004(39):1043-1048.

[8] DENG Baoqing. CFD Simulation of VOCs concentrations in a resident building with new carpet under different ventilation strategies [J]. Building and Environment,2007,(42):297 -303.

[9] 孙斌, 韩克, 蒋能飞.污染源位置对气体污染物影响的数值模拟[J]. 2012,35(2):114-117.SUN Bin, HAN Ke, JIANG Nengfei. Numerical simulation of pollutant source position influencing on air pollutant concentration [J]. Environmental Science &Technology, 2012, 35(2):114-117.

[10] 朱家鲲.计算流体力学[M].北京:科学出版社,1985.ZHU Jiakun. Computational fluid dynamics [M]. Beijing:Science Press,1985.

[11] 张孟威,康德梦. 环境问题的数学解法及计算机应用[M]. 北京:中国建筑工业出版社,1989.ZHANG Mengwei, KANG Demeng. [M]. Beijing: China Architecture & Building Press, 1989

[12] 章梓雄.粘性流体力学[M].北京:清华大学出版社,1998.ZANG Zixiong. Viscous Fluid Dynamics [M]. Beijing:Tsinghua University Press, 1998.

[13] OJIMA Jun. Worker exposure due to reverse flow in push-pull ventilation and development of a reverse flow preventing System[J]. National Institute of Industrial Health, Japan, 2002; 44:391-397

[14] 英克鲁佩勒.弗兰克 P.传热和传质基本原理[M].北京：化学工业出版社, 2011.INCROPERA F P. Fundamentals of Heat and Mass Transfer [M].Beijing: Chemical industry press, 2011.

[15] 陆杰.多污染源共同作用的非线性及边界效应研究[D].大连: 大连海事大学,2008.LU Jie. Nonlinear and boundary effect research under the interaction of multiple pollution sources[D]. Dalian:Dalian Maritime University,2008.

[16] HAZIM B Awbi. 建筑通风[M].北京: 机械工业出版社,2011.HAZIM B Awbi. Building ventilation [M].Beijing:China Machine Press, 2011.