资产证券化的宏观审慎监管——基于网络模型的模拟研究

晏富贵，倪志凌

(1.西安交通大学 经济与金融学院，陕西 西安710061;2.交通银行，上海200122)

一、引 言

金融危机使各国监管当局认识到，仅靠加强单个金融机构的监管不足以维护金融稳定，应当强化金融监管的宏观视野，强化以整个金融体系的系统风险为目标的监测。对宏观审慎监管的强调，是由于在当前的金融系统中，金融机构之间广泛的资产证券化和其他衍生品交易，为系统性风险在金融机构之间的传染提供了直接的渠道，因为资产交易创造了信息外溢[1]，同时资产交易增加了金融机构相互之间的风险暴露[2]。金融机构因此变得相互联系更为紧密，从而在危机发生时放大金融体系的系统性风险[3-5]。

资产证券化等金融创新的引入，使金融机构之间的风险传染呈现出更为复杂的特征。首先，资产证券化和信用衍生品等金融创新的广泛使用，在金融机构之间形成了更为复杂的相互依赖和相互关联，一方面促进了风险的分散，另一方面为风险传染创造了新的渠道。其次，由于引入了资产证券化等金融创新，银行的资产负债表构成更为复杂，一个金融机构的违约会对资产价格造成负面影响，引发新一轮的违约，因为其他金融机构被迫减计资产负债表中的资产价值。

在资产证券化等金融创新得以广泛使用，金融机构之间的风险传染日益复杂的金融系统中，传统的微观审慎监管具有局限，宏观审慎监管因此突显必要性。宏观审慎监管框架是一个动态发展的框架，主要内容包括:对银行的资本要求、流动性要求、杠杆率要求、拨备规则、对系统重要性机构的特别要求，会计标准，衍生产品交易的集中清算，等等[6]。Claudio和 Green[7]指出，宏观审慎监管和微观审慎监管有所不同。在监管目标上，宏观审慎监管的目标是防范金融体系的系统性风险，维护金融体系的稳定，避免经济增长受影响;而微观审慎监管的目的在于控制单个金融机构的风险，保护消费者利益。在相关性方面，宏观审慎监管认为金融机构之间通过资产负债表相互关联，存在着共同的风险暴露，而微观审慎监管则认为金融机构之间不存在相互关联和影响;在校准目标和方式上，由于宏观审慎监管的目标是防范整个金融体系的风险，因而其采取的是自上而下的校准方式，微观审慎监管的目标是防范单个金融机构的风险，因而其采取的是自下而上的校准方式。

为了探讨资产证券化的引入对整个银行系统稳定性的影响，进而探讨为防范系统性风险应当采取的宏观审慎监管措施，我们采用网络模型进行深入分析。我们采用网络模型进行研究，是基于以下几方面的考虑:首先，现有的研究表明，银行系统具有复杂网络结构的特征。其次，外部冲击对于银行稳定性的影响和网络的拓扑结构有密切联系。再次，通过网络理论，可以对资产证券化等金融创新将风险在银行系统中分摊和重新分配，从而对金融稳定造成的影响进行研究，而针对单个银行的信用风险模型等却无法做到这一点。

二、网络模型构建

现实世界的网络既不是完全规则的，也不是完全随机的，而是具有“小的平均最短路径长度”和“大的聚类系数”等特征。Watts和 Strogtz[8]提出的小世界网络模型，能较好反映出实际网络的这两个典型特征。Boss et al.[9]的研究表明，奥地利的银行网络确实具有小世界网络的特征。此外，Barabasi和 Albert[10]发现，现实世界的网络是“无标度”的，也就是说，大多数节点的连接度都很低，但是有少数节点具有很高的连接度。Inaoka et al.[11]表明，银行网络也是一种典型的无标度网络。

已有文献将网络模型用于研究银行信贷的风险传染，但还未见到将网络模型用于研究资产证券化风险传染的先例。本文首次尝试将网络模型用于研究资产证券化对银行体系风险传染的影响，进而讨论针对资产证券化的宏观审慎监管问题。和已有的文献不同，本文基于小世界网络和随机图，并考虑了现实世界银行网络的“无标度”特征来构建网络模型，这样的网络模型更加符合现实银行网络结构的特征，得出的结论更加具有普遍意义。

我们这里建立的网络模型基于小世界网络和随机图，并考虑了现实世界银行网络的“无标度”特征(也就是少数重要银行具有较高的连接度，而大多数中小银行具有较低的连接度)，在此基础上，我们将资产证券化和流动性等因素结合进模型。

第一步，我们在NW小世界网络模型的基础上，结合随机图方法，以及银行网络的“无标度”特征，构建银行网络拓扑图(具体步骤略)。

第二步，构建网络节点资产负债表。

表1 考虑证券化资产的银行节点资产负债表结构

对于每个银行节点而言，必须满足资产负债表约束，也就是资产等于负债。

因此对于银行资产负债表，我们有下列关系式:

上述等式对于所有的i=1，…，都成立。

我们可以根据银行间资产比例、银行资产净值比例等参数，逐步建立单个银行的资产负债表(具体步骤略)。必须注意，在确定每个银行节点的零售资产AR时，银行间负债是为了解决银行短期流动性短缺而存在的，而不是银行进行长期投资的融资手段，因此对每一个银行节点而言，银行间负债与银行间资产的差额必须小于银行的零售资产，也就是说，我们有约束

第三步，构建基于资产负债表的银行风险传染过程。在风险通过银行的资产负债表进行传染的过程中，必须明确几点:第一，银行网络中的节点遭受资产损失(冲击)时，损失首先由银行节点的资产净值吸收，其次由银行间负债吸收，再次由储户存款吸收。第二，如果银行节点遭受的资产损失不足以由银行节点的资产净值全部吸收，那么银行将倒闭。第三，某个银行倒闭后，应该由该银行的银行间负债吸收的资产损失将按比例分摊给该银行的债权银行。第四，通过银行间债权债务关系传递的资产冲击可能引起新一轮的传染性违约，资产冲击沿着传染链条传递下去，直到资产冲击被完全吸收。对于银行网络中的某个银行节点i，在资产负债表中考虑了证券化资产之后，在遭受了损失之后还能够继续运营的条件是:

此处η是银行i遭遇违约的银行间债权占银行的总银行间债权比例，λ是银行i的非证券化银行间资产的平均违约损失率，0＜λ＜1，λ=1对应于零偿还，也就是说当一个和银行i具有债权债务关系的银行违约，银行i损失所有和那个银行相关的银行间债权是银行间的非证券化资产(银行间债权)，SIB是银行间证券化资产，pR(0＜pR＜1)是将不流动的零售资产转卖出售的折价，而pS(0＜pS＜1)是将证券化资产转卖出售的折价，市场流动性越差，资产越急于出售，pR和pS的值越接近0;当资产越能够以接近原价出售时，pR和pS的值越接近1。pSSIB和体现了银行零售资产和证券化资产都按照市值计价的原则。由于证券化资产的流动性要强于零售资产的流动性，因此证券化资产转卖出售时的价值损失要小于零售资产转卖出售的价值损失，也就是通常有pS＞pR。假设银行i的银行间资产中，证券化资产所占的比例为γ，那么非证券化资产`所占的比例就为(1－γ)。

网络中其他银行的倒闭引起银行倒闭的条件，是相对而言的且存在关系式:

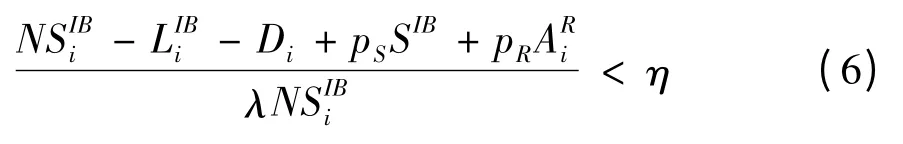
此时银行节点i倒闭的概率为:

为了捕捉资产抛售越多，资产流动性越低，资产折价越严重，从而引发更多银行违约的“流动性螺旋”，我们将pR和pS设置为如下的函数形式:

这里P代表银行资产的折价，P=1代表资产无折价，P=0代表资产的市场价值为零。x是需要出售的资产数量。参数θ衡量的是银行资产价格下降的速度。也就是说，它可以被看作是资产转让市场非流动性的度量。特别地，我们有 P(0)=1以及。换句话说，如果没有资产出售，资产的价格是1，而当x趋向于无穷，资产的价格接近于0。

三、网络模型的模拟分析

根据上述方法，我们采用中国各商业银行的资产负债表(依据最新年报数据)和相互持有资产的情况构建了网络模型实例。我们这里衡量银行系统性风险传染的指标主要有两个，一个是系统性风险的传染概率，另一个是系统性风险的传染范围。在每次模拟中，我们随机选择网络中的一个银行，将这个银行的零售资产清零，如果这个银行的资产损失大于这个银行的资本，那么这个银行节点将倒闭，其部分资产损失将通过银行间连接传递给其他的银行，引起其他银行的倒闭。如果初始银行倒闭，引起了其他银行倒闭，那么我们说发生了系统性风险传染。如果我们在进行的n次模拟实验中，有m次发生了系统性风险传染，那么我们取m/n作为系统性风险的传染概率的度量。如果在进行的n次模拟实验中，每一次模拟都有fi个银行倒闭，那么我们取n次模拟实验银行倒闭的平均值，作为系统性风险传染范围的度量。

我们在考虑资产的流动性效应的情况下，通过模拟实验研究零售资产比例、证券化资产比例、银行网络平均连接度、资本充足率和风险传染频率、风险传染范围之间的关系。这里的流动性效应是指，资产在市场上的抛售数量越多，资产的价格就越低，因此当一个银行倒闭清算，将其资产在市场上卖出时，会引起相应资产价格的下跌，从而引起其他银行持有的相同资产的减值。

(一)零售资产比例、证券化资产比例和风险传染

实验1:在考虑资产的流动性效应的情况下，零售资产比例、证券化资产比例和传染频率的关系。

1.在实验中，当银行网络中的零售资产比例小于20%或者大于80%的时候，银行网络系统性风险传染的频率很低，接近于0。这是因为，我们是通过随机选择网络中的一个银行节点，并将其零售资产清空为零，来给银行网络一个初始冲击。如果银行的零售资产比例小于20%，那么通过清空初始银行节点零售资产的方式，或者不会造成初始银行的倒闭，或者初始银行的倒闭不会引发其他银行的倒闭。因为在零售资产比例小于20%的情况下，和初始银行节点具有债权债务关系的银行，其资本足以覆盖初始银行倒闭带来的资产损失;如果银行的零售资产比例大于80%，那么银行间资产的比例相应就小于20%，在这样的情况下，银行间资产的比例过小，一个银行的倒闭难以通过银行间的信贷渠道造成其他银行的倒闭，因此此时系统性风险传染只能通过资产减值的流动性效应进行，因此风险传染的发生频率比较低。

2.当零售资产的比例在30%到60%之间时，银行网络系统性风险的传染频率较高，此时随着证券化资产占银行间资产比例的增加，银行网络的系统性风险传染频率呈现出波浪起伏的形式。分析形成这样规律的原因，可以认为，银行的长期融资来源可以是其资本金，以及储户的存款;而银行应付流动性危机的短期资金来源，可以通过向其他银行借贷而得，也可以通过出售其持有的证券化资产而得。因此通过出售证券化资产获取短期流动资金，与通过向其他银行借款获取短期流动资金，形成了一种替代关系。在银行网络中，通过银行间借贷关系形成的银行间信贷渠道，既是系统性风险的传播渠道，又是系统性风险的分散渠道。证券化资产比例的上升，降低了银行间借贷关系的重要性，也同时改变了系统性风险传播和系统性风险分散两种具有相反效应的力量对比。在零售资产比例过小、中等、或者过大的情况下，这两种具有相反效果的力量此消彼长的特征不同，造成了系统性风险的传染频率呈现出一定规律的变化。

3.当银行的零售资产大于40%时，那么当银行的证券化资产占银行间资产的比例为70%时，传染频率最小，此时银行的证券化资产占银行总资产的比例大约在20%到40%之间;如果银行零售资产占总资产的比例小于40%，证券化资产占银行间资产的比例在50%以下时，系统性风险的传染频率也较小，此时银行的证券化资产占银行总资产的比例也大约在40%以下。因此，总的来说，为了降低银行网络中系统性风险的传染频率，证券化资产占银行总资产的比例应当控制在20%到40%的范围内。

实验2:在考虑资产的流动性效应的情况下，零售资产比例、证券化资产比例和传染范围的关系。

这里的系统性风险传染范围，也就是在不同的零售资产比例、证券化资产比例情况下，经过100次模拟，计算得到的平均倒闭银行数目。通过实验可以看出，由于证券化资产的流动性效应，系统性风险最多会造成46.54家银行倒闭;相比较而言，经我们计算，如果没有资产的流动性效应，系统性风险最多只会造成平均2.74家银行倒闭。和实验1相比较可以看出，在不同的零售资产比例和证券化资产比例下，当系统性风险传染频率较高时，系统性风险的传染范围也较大。当零售资产的比例在30%到60%之间时，银行网络系统性风险的传染范围较广，此时随着证券化资产占银行间资产比例的增加，银行网络的系统性风险传染范围同样呈现出波浪起伏的形式。类似地，在考虑资产的出售会引起资产价格下跌的情况下，为了降低银行网络中系统性风险的传染范围，证券化资产占银行总资产的比例应当控制在20%到40%的范围内，最多不应当超过40%。

(二)银行网络平均连接度、资本充足率和风险传染

实验3:在考虑了资产流动性效应的情况下，我们考察银行网络的平均连接度、资本充足率和银行系统性风险传染的关系。

1.在实验中我们发现，资本充足率一定时，随着银行网络平均连接度的增加，网络的传染频率呈现出“M”型。当平均连接度在20附近时，传染频率会到达一个较低的水平。当银行网络的平均连接度达到45以上时，整个银行系统的传染频率也接近于零。这是因为，一方面，银行和银行之间的连接是风险传染的渠道，另一方面，银行和银行之间的连接也是风险分散的渠道。当银行间的连接数很少的时候，银行间平均连接度的增加，增大了系统性风险在银行间的传染机会;当银行间的连接数中等的时候，银行间平均连接度的增加，一方面增大了风险传染的机会，另一方面也将风险分散给了更多的银行;而当银行系统的连接数进一步增加的时候，银行间连接的风险分散效应开始占优，银行系统性风险的传染频率开始不断减小。此外，还可以看出，提高银行资本充足率对降低传染频率有一定效果，但是效果不是很理想。例如当资本充足率达到8%时，传染频率还一度超过0.6。

2.给出了在考虑资产流动性效应的情况下，资本充足率一定时，平均连接度和传染范围的关系。

在资本充足率一定时，银行网络平均连接度和网络的传染范围之间，同样呈现出“M”型的关系。当银行网络的平均连接度在20附近时，银行系统性风险的传染范围达到一个低谷;而当银行网络的平均连接度大于45时，只要资本充足率大于等于2%，银行网络中就只有一家银行倒闭。通过提高资本充足率降低传染范围的效果会非常显著。只要资本充足率大于8%，银行网络中倒闭银行的数目就在2家以内。

3.在平均连接度一定时，资本充足率和传染频率的关系。

随着银行的资本充足率不断增加，银行系统性风险的传染频率不断下降，但是对于不同的平均连接度，传染频率下降的速度并不相同。当银行系统的平均连接度在30以下的时候，随着银行资本充足率的提高，银行系统的风险传染频率缓慢下降，当资本充足率达到2%的时候，传染频率在0.4附近，当资本充足率达到8%的时候，还有较低频率的系统性风险传染发生;而当银行系统的平均连接度大于40的时候，随着银行资本充足率的提高，银行系统的风险传染频率急剧下降，资本充足率只要达到2%，系统性风险的传染频率就接近于零。

4.在平均连接度一定时，资本充足率和传染范围的关系。

当资本充足率增大的时候，银行网络的系统性风险传染范围随之不断降低，只要资本充足率高于5%，整个银行网络中基本上就只有受到初始冲击的那个银行倒闭。一般来说，银行网络的平均连接度越高的时候，资本充足率的微小增加，就会引起风险传染范围的迅速降低。对比实验3中的3和4可以看出，在一定的平均连接度和资本充足率下，传染频率高的时候，传染范围不一定广。例如在资本充足率为4%的情况下，如果网络的平均连接度为10，那么一个银行受到传染的概率为24%，而从传染范围来看，在100家银行中，平均仅有1.42家银行倒闭。对比实验3中的1、2、3和4可以看出，在考虑资产流动性效应的情况下，和提高银行网络的平均连接度相比，提高资本充足率对降低系统性风险的传染范围具有更为显著的效果;而和提高资本充足率相比，提高网络的平均连接度对降低系统性风险传染频率的效果更为显著。

(三)资产证券化前后，银行网络平均连接度、资本充足率和风险传染

我们现在比较在银行体系积极从事资产证券化业务之后，与银行体系积极从事资产证券化业务之前，网络的平均连接度、资本充足率和系统性风险的传染频率、传染范围之间的相关关系有何不同。根据发达国家证券化之前和之后的银行数据，我们作出如下合理假设:在证券化引入银行系统之前，银行系统的零售资产占总资产的比例为80%，而证券化资产占银行间资产的比例为0%。在证券化引入银行系统之后，银行系统的零售资产占总资产的比例为60%。

在证券化引入银行系统之后，我们分两种情况讨论资产的流动性效应，一种情况是由于证券化资产的流动性比零售资产的流动性高，那么出售同样数量的资产，证券化资产的折价要比零售资产的折价少;另一种情况是由于证券化资产被错误定价，以及由于证券化资产过于复杂，其风险不能被投资者准确识别的情况下，出售同样数量的资产，证券化资产的折价要比零售资产的折价高。根据美国次贷危机期间的数据，我们作出如下合理假设:对于第一种情况，我们假设如果整个银行系统将其所拥有的零售资产在市场上出售50%，则零售资产的价格下降为最初价格的50%，如果将证券化资产在市场上出售50%，则证券化资产的价格下降为最初价格的65%;对于第二种情况，我们假设如果整个银行系统将其所拥有的零售资产在市场上出售50%，则零售资产的价格下降为最初价格的50%，如果将证券化资产在市场上出售50%，则证券化资产的价格下降为最初价格的35%。

在考虑了资产流动性效应的情况下，如果银行网络的平均连接度小于等于15(也就是和某家银行有借贷关系的银行数量小于等于15家)，同时资本充足率小于等于6%，那么在银行体系积极从事资产证券化业务之前，银行网络系统性风险的传染频率更高;而在银行体系积极从事资产证券化业务之后，银行网络系统性风险的传染频率会相应降低;如果银行网络的平均连接度大于等于40，并且资本充足率大于2%，那么在银行体系积极从事资产证券化业务之后和积极从事资产证券化业务之前一样，传染频率都为0。在网络平均连接度和资本充足率的其他范围内，积极从事资产证券化业务之后会比积极从事资产证券化业务之前，系统性风险的传染频率更高。此外，同样抛售50%的证券化资产，证券化资产的价格变为原价的35%，就要比证券化资产的价格变为原价的65%的情况下，系统性风险的传染频率更高。证券化之前，银行网络的平均传染频率是0.073;证券化之后，如果抛售50%的证券化资产，证券化资产的价格变为原价的35%，平均传染频率为0.101，如果抛售50%的证券化资产，证券化资产的价格变为原价的65%，平均传染频率为0.078。在考虑了资产流动性效应的情况下，银行体系积极从事资产证券化业务之前，提高资本充足率对降低银行网络系统性风险传染频率的作用更大;而在银行体系积极从事资产证券化业务之后，提高资本充足率对降低银行网络系统传染频率的作用相比而言较小。从具体的数字来看，在银行体系积极从事资产证券化业务之前，如果资本充足率提高到10%，那么不论银行网络的平均连接度如何，网络中系统性风险的传染频率将降为0;而在银行体系积极从事资产证券化业务之后，即使资本充足率提高到15%，当网络的平均连接度为5时，不论证券化资产的折价是高还是低，仍然有超过0.18的传染频率存在。

此外，通过对比证券化前后的两类实验可以发现，在银行体系积极从事资产证券化业务之前，银行网络系统性风险的传染范围较小;而在银行体系积极从事资产证券化业务之后，银行网络系统性风险的传染范围会更广。从具体数字来看，在银行积极从事资产证券化业务之前，银行网络中系统性风险传染范围的平均值(100家银行中倒闭银行的平均数目)为3.46，而在银行体系积极从事证券化业务之后，如果证券化资产出售一半降价65%，平均传染范围为 4.06;如果证券化资产出售一半降价35%，那么平均传染范围为6.53。在银行体系积极从事资产证券化业务之后，通过单独增加银行网络的平均连接度或者增加银行体系的资本充足率，减少系统性风险传染范围的作用会降低。在银行体系积极从事资产证券化业务之前，只要将银行网络的平均连接度增加到45以上，或者将银行的资本充足率提高到10%以上，单个银行的倒闭就不会引起其他银行的倒闭;在银行体系积极从事资产证券化业务之后，如果采取单独措施的话，单独把银行网络的平均连接度增加到50以上或者单独将银行的资本充足率提高到15%，单个银行倒闭仍然有可能造成其他银行倒闭。虽然如此，但是如果采用双管其下的方法，在增加银行网络平均连接度的同时，增加银行的资本充足率，那么如果将银行网络的平均连接度增加到45以上，同时将银行的资本充足率提高到2%以上，单个银行的倒闭就不会引起其他银行的倒闭。因此在引入证券化之后，要降低银行系统的传染范围，就需要从提高银行网络的平均连接度和增加资本充足率两方面同时着手。

四、主要结论

本文采用网络模型研究资产证券化等创新业务引入后，银行网络的系统性风险传染频率、传染范围具有怎样的规律。本文在考虑资产的流动性效应的情况下，分别研究了零售资产比例，证券化资产比例、资本充足率、银行网络的平均连接度等因素的变动对系统性风险的传染频率、传染范围的影响。主要结论如下:

1.在资本充足率一定的情况下，银行网络平均连接度和网络的传染频率、传染范围之间，呈现出“M”型的关系。在网络平均连接度一定的情况下，银行网络的传染频率、传染范围和资本充足率之间，呈现出单调递减的关系。网络平均连接度和网络的传染频率、传染范围之间“M”型关系的出现，是因为银行间由于债权债务关系或者由于相互之间的证券化交易形成的连接既是风险传播的渠道，又是风险分散的渠道，风险分散效应和风险扩散效应在不同时候强弱对比不同。

2.在发展程度不同的金融市场引入资产证券化业务，风险传染范围和风险传染频率呈现不同的规律。

(1)在发展还不完善的金融市场中，也就是在银行网络的平均连接度小于15，平均核心资本充足率小于6%的时候，不论是否考虑资产的流动性效应，引入资产证券化业务将会降低系统风险的传染频率，但会增加系统风险的传染范围。因此在发展还不太完善的金融市场中引入资产证券化等创新业务，会降低系统性风险发生的可能性，但是系统性危机一旦发生，就会影响程度更大，影响范围更广。

(2)在发展相对完善的金融市场中，也就是银行网络的平均连接度在30附近时，如果不考虑资产的流动性效应，并且银行资本充足率和银行网络的平均连接度保持不变，那么随着证券化资产比例的不断升高，系统性风险的传染频率和传染范围将会先升高而后下降，因此在一段时期内，证券化等金融创新可持续推动到一定阶段，使得银行系统的风险传染频率和传染范围到达一个顶峰后逐步下降。如果考虑资产的流动性，那么为了降低银行网络中系统性风险的传染频率，以及系统性风险的传染范围，证券化资产占银行总资产的比例应当控制在20%到40%的范围内，最多不应当超过40%。

(3)如果金融市场的发展非常完善，银行网络中的每个银行都和其他银行建立了较为充分的连接，也就是网络的平均连接度大于等于40时，如果银行间的相互连接不会因为受到外部冲击而中断，那么只要银行的核心资本充足率大于2%，银行网络中一个银行的倒闭就难以引起其他银行的倒闭。

3.单独增加资本充足率对降低风险传染范围效果较为显著;而单独增加银行网络的平均连接度对降低风险传染频率效果较为显著。但是在引入资产证券化业务后，采用单一手段降低风险传染频率及风险传染范围的效果将明显降低。因此在引入资产证券化等创新业务后，必须采用综合的手段，同时增加银行网络的平均连接度和资本充足率，才能有效降低风险传染的概率和范围。

4.证券化资产的折价程度对系统性风险传染的广度和深度有显著影响。证券化资产的折价，一方面通过资产负债表造成和倒闭银行有直接关联的其他银行资产减记，另一方面则由于采用盯市(mark-to-market)公允会计原则造成更大范围的银行资产减记。在同样的网络连接度和资本充足率情况下，证券化资产的折价程度提高，将显著增加系统性风险的传染频率和传染范围。证券化资产的折价程度，和证券化资产的信用评级、证券化市场的流动性、证券化市场透明程度、证券化资产的定价准确程度都有关系。当危机时，证券化资产抛售越多，证券化资产流动性越低，资产折价越严重，会引发更多银行违约的“流动性螺旋”。

五、宏观审慎政策建议

在引入资产证券化等创新业务后，如何保持金融系统的稳定，以往的政策措施都将重点放在防范单个金融机构风险的微观审慎层面之上。而上面的研究结果表明，资产证券化业务的引入将显著影响系统性风险的传染特征，因此从宏观审慎的角度考虑资产证券化的风险防范问题有其必要性。根据上述研究结论，从宏观审慎的角度来看，笔者提出下列政策建议:

第一，强化资本要求。上面的研究结果表明，在网络平均连接度一定的情况下，随着核心资本充足率的提升，系统性风险的传染频率、传染范围随之单调下降。这表明强化资本要求，是增强银行抵御风险能力，防范风险传染的基础。资本包括普通股、优先股、附属债、长期债等不同种类，吸收损失的能力各不相同。普通股吸收损失能力最强，应当扩大核心资本的比重，提高普通股在总资本中的占比。在银监会新颁布的《中国银监会关于中国银行业实施新监管标准的指导意见》中，核心一级资本充足率、一级资本充足率和资本充足率分别不低于5%、6%和8%，此外还要计提2.5%的留存超额资本要求和0-2.5%的逆周期超额资本。银行在按照银监会要求提升资本充足率水平的基础上，还应当考虑应急可转债(CoCos)的安排。当银行资本充足率低于预设水平时，应急可转债强制性转为普通股，从而应急性提高资本水平。

第二，鼓励和维持适当的银行间相互交易。根据网络模型的模拟结果，一方面，在引入资产证券化等创新业务后，必须同时增加银行网络的平均连接度和提高资本充足率，才能有效降低风险传染频率和风险传染范围。银行网络平均连接度的提升，需要依赖于银行通过相互持有金融资产、例如资产支持证券和衍生品，形成更为密切的债权债务，以及或有债权债务关系。因此推出更多在银行间市场交易的金融新产品，扩大银行间市场的交易规模，提高银行间市场的流动性，使银行通过相互的资产交易联系更为紧密，有利于降低系统性风险。另一方面，对于银行间的相互交易也要加以适当控制。在资本充足率一定的情况下，银行网络平均连接度和网络的传染频率之间“M”型的关系表明，银行间的联系既非越少越好，也非越多越好，银行间的交易规模和联系紧密度，都应当维持适中水平。根据我们的模拟结果，银行间平均连接度在20左右较为合适。当遭遇危机时，通过向市场注入流动性，维持银行之间的适度的交易规模和连接度水平，也显得非常重要。

第三，金融机构持有的证券化资产规模应当控制在一定范围内。前面网络模型的模拟结果表明，如果考虑到资产的流动性效应，在银行间连接度适中的情况下，为了降低银行网络中系统性风险的传染范围，证券化资产占银行总资产的比例应当控制在20%到40%的范围内，最多不应当超过40%。此外，对于同类标的物的资产支持证券，不应当集中于某一家或者某几家金融机构持有，应当确保对于同类资产支持证券(例如都以房地产抵押贷款为标的物的资产支持证券)的持有尽量分散，控制单一金融机构持有同类资产支持证券的比例。

第四，当具有系统重要性的大银行遭遇流动性风险时，央行作为最后贷款人应当有及时救助的对策和措施。通过网络模型的分析可以发现，不同规模的银行在系统性风险传染过程中的作用是不同的。具有系统重要性的大银行，与其他银行的联系更为紧密，通常也是资产证券化等创新产品集中交易的对手方。当资产证券化市场和信用衍生品市场出现危机时，这些银行往往也最先遭遇流动性危机。央行作为最后贷款人对这些银行进行及时救助，能有效阻止系统性风险在银行体系的进一步扩散。但是救助也应当有一定限制条件，防止“太大而不能倒”的金融机构出现道德风险问题。

第五，采取措施降低危机时证券化资产的折价程度。首先，提高市场的透明度，完善信息披露制度。网络模型的模拟研究表明，如果信息不透明，投资者无法准确评价其风险，那么危机来临时，金融机构持有的证券化资产，会由于投资者将证券化资产恐慌性抛售而加速贬值，同时，金融机构因为不清楚自己持有的风险暴露到底有多大，而不愿意向其他金融机构提供信贷，造成银行系统中银行间连接度的降低，这些都会显著增加系统性风险的传染频率和传染范围。其次，完善资产证券化的定价和评级机制。一方面要研究不同市场状况下确定证券化资产合理价格的方法，另一方面改革评级机构的评级机制，降低市场参与者对评级机构的依赖，市场参与者不应当将评级机构对评级的调整作为抛售证券化资产的自动触发器。再次，对会计准则中公允价值再审视，确立合理的金融工具计量和减记方法，降低因证券化资产折价引发“流动性螺旋”的可能。

[1]Aghion P，Bolton P，Dewatripont M.Contagious bank failures in a free banking system[J].European Economic Review，2000，44:713-718.

[2]Freixas X，Parigi B，Rochet J C.Systemic risk，Interbank relations，and Liquidity provision by the central bank[J].Journal of Money Credit ＆ Banking，2000，32(3):611-638.

[3]Elsinger H，Lehar A，Summer M.Risk assessment for banking systems[J].General Information，2006，52(9):1301-1314.

[4]Acharya V V，Yorulmazer T.Too many to fail-an analysis of time-inconsistency in bank closure policies[J].Journal of Finance Intermediation，2007，16(1):1-31.

[5]Wagner W.The homogenization of the financial system and financial crises[J].Journal of Financial Intermediation，2008，17(3):330-356.

[6]周小川.金融政策对金融危机的响应——宏观审慎政策框架的形成背景、内在逻辑和主要内容[J].金融研究，2011(1):1-14.

[7]Borio C，Green C J.Implementing the macroprudential approach to financial regulation and supervision[J].Financial Stability Review，2009(13):31-41.

[8]Watts D J，Strogatz S.Collective dynamics of smallworld networks[J].Nature，1998，393(6684):440-442.

[9]Boss M，Elsinger H，Thurner M S S.Network topology of the interbank market[J].Quantitative Finance，2004，4(6):677-684.

[10]Barabási A，Albert R.Emergence of scaling in random networks[J].Science，1999，286(5439):508-512.

[11]Inaoka H，Ninomiya T，Taniguchi K，et al.Fractal network derived from banking transaction—— An analysis of network structures formed by financial institutions——[R].Bank of Japan Working Paper No.04-E-4，2004.