三维模型下电解加工过程的模拟
何长运,黄志刚,郭钟宁,唐 怡
(广东工业大学机电工程学院,广东广州510006)
在电解加工过程中,由于工件阳极和工具阴极并不直接接触,故无表面内应力和切削力,因而加工变形小。同时,由于工具阴极上发生的电化学行为只是析氢反应而无溶解,所以工具电极无损耗。虽然电解加工具有很多优点,但同时也受多种因素的影响,准确预测工件的成形形状对提高加工质量至关重要。
随着计算机技术和计算方法的发展,利用数值模拟方式对电解加工进行仿真,在工业中已越来越重要。最初通过经验公式预测工件成形,尽管能在一定程度上对加工形变进行预测,但其使用范围和精度受到很大限制,且需进行大量工艺实验以确保经验公式的准确性。早在20世纪60年代,Tipton[1]最先将有限差分的方法应用到电解加工过程的模拟中。为了模拟出加工形貌变化,在处理工件表面点的运动轨迹时,用曲面法线的垂直分量近似代替法线方向。该方法处理的工件形变,其最终结果与实际加工相符,但加工过程中任意时刻的形貌则与实际情况不符。Jain等[2]将有限元法运用于电解加工,用三角单元将电极区域网格化,求出了平行板电极间的电流密度分布,同时获得了加工间隙中的温度分布。Deconinck等[3-5]提出了一种随时间变化的多物理场数值模型来深入研究电化学加工过程。该模型结合电中性条件和电极-电解液界面极化下的线性温度关系,成功模拟出电解液传质(迁移、扩散和对流)对电流密度的影响。但上述模拟都是建立在二维模型下的,对于一些复杂形状的工具则无法模拟。因此,研究三维模型下电解加工过程的仿真对实际电解加工极为重要。
本文提出了一种利用任意拉格朗日-欧拉法(ALE)和重新划分网格的方法来处理三维模型的曲面变形,并利用有限元法模拟加工间隙内的电流密度分布,两种方法的结合能更真实地获得实际加工中的三维变形。
1 任意拉格朗日-欧拉法
在描述有限元网格运动的方法中,Lagrange方法是将网格固定在运动的物质点上随其运动:

式中:x为空间位置坐标;X为研究物质点;t为时间。这在描述运动界面或运动边界时非常有效,但在处理物质大变形时会引起网格纠缠,不仅影响了单元近似精度,还会因坐标变化中雅可比行列式(Jocobian)的值≤0而导致计算终止或局部范围误差严重。
而Euler处理方法则是网格节点固定不动:

式(2)描述了同一个空间位置点x在不同时刻下被物质点占据的情况,因此,在处理大变形时不会引起网格纠缠,但却无法精确确定运动界面或运动边界的位置。
为了克服上述方法的缺点,于是便有了任意拉格朗日-欧拉法(ALE)。该方法引入一个可独立于现实构型和初始构型的参考构型,在物体发生变形的过程中,观察者随参考构型一起运动;相对于观察者,参考构型为固定不动,而现实构型和初始构型则都相对于参考构型运动:

式 (3)为物质X在参考坐标系η中的运动规律;式(4)为参考点在空间坐标系中的运动。图1是参考坐标系下的网格运动。

图1 参考坐标系下的网格运动
在物质描述方法中,有限单元法对物体网格划分,网格点即为物质点,所以网格是随物质一起运动的。在空间描述方法中,有限单元法对空间网格划分,网格点即为空间点,所以网格在空间中固定不动。在ALE描述方法中,有限单元法对参考构型网格划分,网格点即为参考点,网格是独立于空间和物质运动的,可根据需要自由选择。

当物质点X在时刻点t时,其在空间的运动速度v与其在空间位置矢量x=x(X,t)对应的导数相等:

参考点η在空间的运动速度即为网格点运动速度v′,它是网格点η在空间的位置矢量x=x(η,t)的时间导数:

物质点X在参考坐标系中的速度为位置矢量η=η(X,t)对时间的导数:

在ALE方法中,计算网格的运动规律可任意给定。将ALE方法分情况退化为拉格朗日方法和欧拉方法来处理网格的运动规律:
(1)当 v′=0 时,计算网格在空间中固定不动,用欧拉方法;
(2)当 v′=v 时,计算网格随物质一起运动,用拉格朗日方法;
(3)当 v′≠v≠0 时,计算网格自由运动,用一般ALE方法。
综上所述,运用ALE方法可精确模拟大变形中运动界面的位置变化。在处理微细电解打孔问题时,工件表面形貌变化为大变形,因此,ALE方法能有效解决三维模型形变的问题。
2 加工区域电场模型的建立
基于法拉第定律,建立电解加工间隙内的电场仿真模型,为便于分析,本文采用二维数学模型。如图2所示,5为阳极工作边界,1为阴极工作边界,其余为自由边界,各边界组合形成了阴、阳极间的封闭区域Ω。模型中,阴、阳极间的加工间隙Δ为0.1 mm,阴极直径d为0.2 mm,电解液选取质量分数为15%的NaNO3溶液,电导率κ为11.6 S/m,阳极工件材料选取0Cr18Ni91,体积电化学当量ω为0.002 16 cm3/A·min。仿真中,取电流效率 η=1,加工电压U=10 V。
研究电解加工成形规律时,一般认为加工过程已进入平衡状态。此时,电场参数不随时间变化,而只是位置的函数,因此,加工间隙内的电场可视为无源稳恒电流场。且由于仅考虑电场分布,故可假设电解液为各向同性。由电场理论可得电位分布符合拉普拉斯方程:
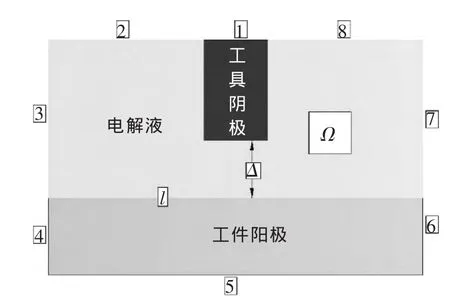
图2 加工区域电场模型

或写作:
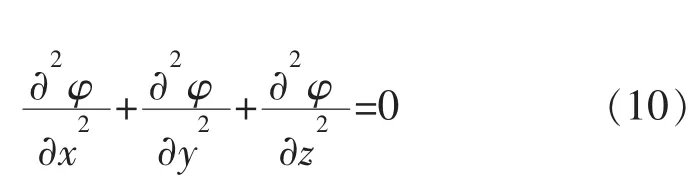
电解加工的工具阴极和工件阳极均为金属导体,其电位分布可看做不同电位的等位面:

式中:φ 为电场中各点的电位, 一般 φ=φ(x,y,z);U为阳极表面电位值。
其他边界符合第二类边界条件:

空间各点的电场强度等于该点电位梯度的负值:

在电解液中,电流密度与电场强度、电导率的关系为:

式中:κ为电解液的电导率,它主要受电解液浓度、温度和气泡率等因素的影响。
根据法拉第第一定律可得被加工金属的表面蚀除速度:

式中:η为电流效率,与阳极金属表面各处的电流密度有关;ω为金属的体积电化学当量,即单位电量溶解金属的体积,它与电解液浓度和工件材料有关。
综上所述,根据求解可得到金属表面的蚀除速度,再利用任意拉格朗日-欧拉法便可获得电解加工过程中工件表面的形貌变化。
3 仿真模拟
利用COMSOL Multiphysics软件进行仿真模拟,先建立有限元模型,再定义各区域的材料属性,包括电导率和介电常数(金属的介电常数为1)。阴、阳极两端分别施加外部电压,阴极接地,阳极为工作电压U,最后进行有限元网格划分,通过计算可获得加工间隙内的电场强度分布(图3)。
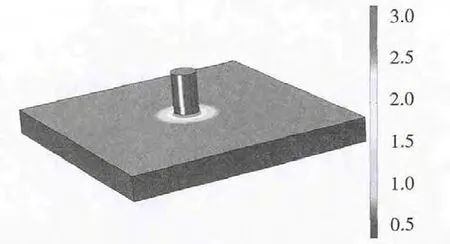
图3 加工间隙电场分布
由电场强度分布可看出,无掩膜电解加工的杂散腐蚀较严重,故加工出的小孔开口较大(图4)。为获得开口较小的小孔,可在阴极表面涂覆一层光刻胶,光刻显影后作为掩膜来约束杂散电场的分布,即可提高加工质量(图5)。

图4 无掩膜加工效果

图5 有掩膜加工效果
值得注意的是,在进行网格划分时,加工区域的网格应密集一些,目的是为了获得电场强度的精确分布及防止计算过程中因网格畸变导致局部计算严重出错(图6)。

图6 网格畸变后加工表面的变形
在仿真模拟过程中,应用任意拉格朗日-欧拉法虽能模拟出工件的加工变形,但无法模拟出圆孔的打穿。因为圆孔一旦打穿,该处的材料将会由阳极材料变为电解液材料,所以只能无限地接近于打穿。为清晰说明问题,采用如图7所示的截面图。

图7 t=15 min时加工间隙内的电场强度分布
如果要模拟打穿后的电解加工,可对模型进行适当处理:在工件下方重新建立一个较薄的立方块,利用布尔运算中的差集运算,将模型减去新建的立方体,可近似获得打穿后的模型;再将处理后的模型作为初始模型重新计算,可进行打穿后电解加工过程的模拟(图8)。

图8 打穿后的电场强度分布
由图8可看出,工件表面c、d处的电场强度集中,该区域在后续加工中的腐蚀速度较快。为保证加工圆孔的刃角,应合理控制加工时间,否则会出现实际加工的圆孔打穿现象(图9)。
4 结语

图9 实际电解加工中圆孔打穿
本文利用任意拉格朗日-欧拉法和重新划分网格的方法获得了电解加工中被加工面的三维曲面变化,并模拟出工具掩膜下的小孔成形。对于小孔打穿的模型也提出了解决方案,为后续提高电解加工质量提供了理论依据。
[1] Tipton H.Dynamics of ECM process[C]//Proceeding of 5th International MTDR Conference.Birmingham,UK,Pergamon,Oxford,1964:505-522.
[2] Jain V K,Pándey P C.Finite element approach to the two dimensional analysis of electrochemical machining[J].Precision Engineering,1980,2(1):23-28.
[3] Deconinck D,Van Damme S,Deconinck J.A temperature dependent multi-ion model for time accurate numerical simulation of the electrochemical machining process.Part I:Theoretical basis[J].Electrochimica Acta,2012,60:321-328.
[4] Deconinck D,Van Damme S,Deconinck J.A temperature dependent multi-ion model for time accurate numerical simulation of the electrochemical machining process.PartⅡ:Numerical simulation [J].Electrochimica Acta,2012,69:120-127.
[5] Deconinck D,Hoogsteen W,Deconinck J.A temperature dependent multi-ion model for time accurate numerical simulation of the electrochemical machining process.PartⅢ:Experimental validation [J].Electrochimica Acta,2013,103:161-173.

