钢框架优化设计及其抗震性能分析
薛建阳,黄小刚,高卫欣,韩 琛,翟 磊
(西安建筑科技大学土木工程学院, 陕西 西安 710055)
近年来钢结构在我国的应用越来越广泛.在多高层钢结构中,钢框架体系(包括钢框架-支撑结构与纯钢框架结构)大量出现在钢结构住宅和钢结构厂房中,已经成为一种常见的结构体系.钢框架有良好的综合经济性能,包括施工速度快,可以减少基础造价和增加建筑面积等,发展建筑钢结构产业将成为国家的宏观政策,传统的钢结构设计方法得到的计算结果较为保守,因此有必要对钢框架体系进行优化设计,这对我国钢结构的推广有很大的促进作用.国内外很多学者[1-3]已经做了一些优化设计研究,取得了显著的经济效益,但仍是基于以用钢量最小为目标函数的单目标优化,在受动力荷载作用时动力响应一般较大.目前遗传算法[4]等现代技术也被用于结构优化,但其在优化中常常出现“早熟”现象,需要采用编程语言对其改进后实现在结构工程中的应用.由于结构优化设计的目标变量常常不止一个,Ali[5]等以建筑物工程初始成本和全寿命周期震害成本为目标变量,对钢框架进行基于性能的多目标优化,并提出采用NSGA-II算法来解决这类优化问题.在分析中如果能使结构地震作用产生的应变能减小也可降低震害成本.因此本文的优化综合考虑了结构耗钢量和地震作用产生的应变能,以体积和应变能最小为目标函数对钢框架进行了多目标优化.
1 算例基本参数
图1为单榀两跨五层的钢框架,抗震设防烈度为8度,抗震等级为三级,场地特征周期Tg=0.4 s,竖向荷载的取值原则如下:主梁自重(折算为均布荷载)和主梁上的墙体荷载按均布荷载计算,作用在主梁上,次梁传递的荷载为集中荷载,作用于主次梁连接处.表1列出了该框架梁柱采用的H型钢截面,材质为Q345B钢,节点采用现场焊接,分析时假定为刚性连接.梁、柱的单元模型均选取单元BEAM188,并采用OPT模块在材料弹性范围内进行优化,根据规范分四种工况进行优化分析,工况1:1.35恒载+0.7(1.4左风+1.4活载),工况2:1.35恒载+0.7(1.4右风+1.4活载),工况3:1.2重力荷载代表值+1.3左地震作用,工况4:1.2重力荷载代表值+1.3右地震作用[6-7].

图1 原框架结构简图(mm)Fig.1 Diagram of frame structure

表1 原框架构件截面Tab.1 Original frame components section
抗震钢框架的总应变能(Strain Energy)计算公式为:

其中:n为总层数;m为参与组合的振型数.Pij为第j振型下第i层的地震力,δi为相应的侧移,在ANSYS中通常把把结构的重力荷载代表值换算为质量元(MASS21)的实常数进行模态分析后计算结构的地震作用,经计算可不考虑二阶效应.
2 多目标优化算法的选择
2.1 约束法及TOPSIS法
多目标优化一般得不到同时满足各个目标的最优解,只能从非劣解集中找到最适宜的均衡解来最大程度地逼近每个目标的要求[8].因此处理多目标优化需要解决非劣解的生成方法,多目标决策技术和优化方法等多个问题来完成数学模型的建模.
约束法是一种传统的生成非劣解的方法,其基本思路是在所有目标中选择一个作为主目标,把其他目标函数转化为主目标的约束条件来建立单目标优化模型,一般形式记为:

其中,εi为第i个目标的上限值(i=1,2,…,m且i≠k).
本文通过以体积最小作为优化的主目标,应变能最小作为主目标的约束条件,将多目标优化问题转化为单目标数学模型来求解,可以简单有效的得到多目标优化结果的非劣解集,从非劣解集中找到一个最佳的均衡解有很多方法,为了便于编写成APDL参数化语言,同时计算简单直观,决策原则采用基于理想点的决策方法(TOPSIS法).
TOPSIS方法首先需要确定问题的理想解和最不理想解,然后在非劣解集中找到一个方案,使其距离理想解最近,又距离最不理想解最远,在度量前首先要将多目标问题规范化:

其中,fij为第j个目标对于第i个可行方案的优化结果,并假设Z*为规范化后的理想点,Z-为最不理想解.容易算出,某一非劣解对于理想解的相对接近度Ci为:

2.2 优化采用的数学模型
工程应用中需要把实际工程问题转变为合适的优化数学模型,优化问题使用三类变量来描述结构参数,即设计变量,状态变量和目标函数[9].结构的跨度,层高等参数由建筑要求确定,因此我们只选择梁、柱的截面尺寸作为优化的设计变量.在数学模型中状态变量为目标函数的约束条件,对钢结构优化而言包括强度条件,柱的稳定性验算,位移条件,受压构件长细比,翼缘外伸部分宽厚比和腹板高厚比等.
梁、柱的截面尺寸包括H型钢的高,宽,翼缘厚度和腹板厚度,当设计变量较多时,如果设计初值离最优值的差距较大,直接使用ANSYS优化模块中的一阶寻优法耗时会很长,还有可能不收敛得不到最优解,但得到的优化曲线较为光滑,其一次迭代等价于多次循环分析,精度较高.函数逼近法获得的优化结果比较离散,对于较多的设计变量,其得到的优化结果经常不能满足所有的约束条件.因此通常将函数逼近法和一阶寻优法搭配使用.
3 无支撑钢框架多目标优化
为了将约束法及TOPSIS法运用到钢框架多目标优化中,本节基于ANSYS平台对上述钢框架进行了多目标优化设计.在此以工况1的计算为例进行说明,分别把体积V最小和应变能SE最小作为钢结构优化的目标函数进行单目标优化,结果如表2所示:

表2 不同目标函数下的优化结果Tab.2 Optimizing results under different objective function
通过表2确定εi的变化范围,,i=0,1,…,n-1,在以体积最小(Volume)为目标函数的单目标优化中增加约束条件(OPVAR, SE, SV,εi,εi+1),便可产生n个非劣解,表3为n=6时的优化结果.

表3 约束法生成的非劣解Tab.3 Pareto solutions by constraint method
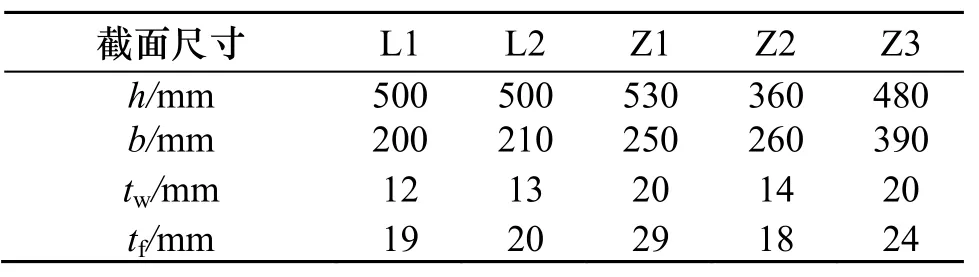
表4 优化后构件截面Tab.4 Optimized components section

表5 优化后部分状态变量Tab.5 The optimized partial state variables
根据表3可知当i=2时为工况1下的均衡解,通过同样的方法可得到其他工况下的均衡解,并将四种工况求得的每个设计变量的最大值列于表4,作为多目标优化后的最终截面,由于优化中将决策变量假定为连续值,故需对结果进行取整处理.另外提取优化后结构在各工况下的部分状态变量,如表5所示,可以看出梁、柱各截面的应力值均低于限值,柱长细比和最大层间位移角对优化结果起控制作用.
4 带支撑钢框架拓扑优化
在单目标优化时以体积最小为目标函数得到的钢框架中梁、柱的强度均未达到规范限值,但其层间位移角接近1/250,导致算得的应变能较大.为增大结构的抗侧向刚度,在此钢框架的基础上增加支撑,并对拟采用的支撑体系进行多工况载荷下的静力拓扑优化,ANSYS采用变密度法通过改变单元伪密度来确定支撑杆件的最佳布置位置.钢框架模型的网格尺寸为H/300,其中H为结构总高度,梁、柱所在区域的网格不进行优化.拓扑优化的目标变量为竖向荷载+向左的地震力组成的工况1和竖向荷载+向右的地震力组成的工况2两者分别作用下的柔度组合量,加权系数均为0.5,体积减小最高限为75%.图2(a)为迭代25次后拓扑优化得到的“桁架”型结果,将支撑的拓扑形状转化为相应的支撑杆件,一~三层支撑取H175×175×8×12 mm,四、五层支撑取H175×150×6×8 mm,如图2(b)所示,增加支撑后的框架梁、柱的截面应力在8度多遇地震作用下也小于规范规定的限值.
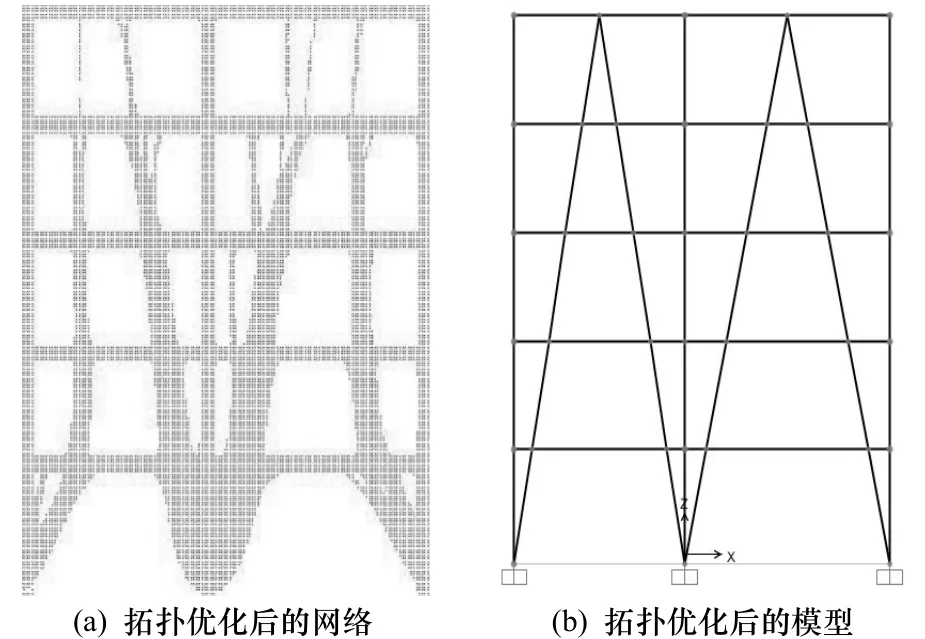
图2 钢框架—支撑拓扑优化过程Fig.2 Topology optimization of braced steel frame
5 不同优化模型的地震反应对比
表6为四种不同优化工况下得出的结构体积对比.为了评价和对比不同优化模型的抗震性能,有必要对四种工况下的结构分别进行推覆分析和弹塑性时程分析[10-11].

表6 优化后结构体积对比Tab.6 Comparison of the volume of optimized structures
5.1 推覆分析
取优化后的梁、柱截面分别建立有限元模型,为了评价优化结构的性能,采用振型加载法对结构进行推覆分析,控制位移的最大值取为结构高度的1/50,根据各构件的受力特点,分别在梁、柱和支撑的相应位置设置集中塑性铰,塑性铰采用基于FEMA356规范的默认铰属性,图3为优化后的结构基底剪力随顶点位移的变化情况,从图可以看出,带支撑钢框架的顶点位移在达到控制位移后曲线刚达到平台区,说明支撑作为结构的第一道抗震防线,有效避免了框架梁、柱过早进入塑性状态,其基底剪力峰值比原结构高约7.2%.而单目标优化后的纯框架基底剪力峰值比多目标优化后降低了约14.3%.
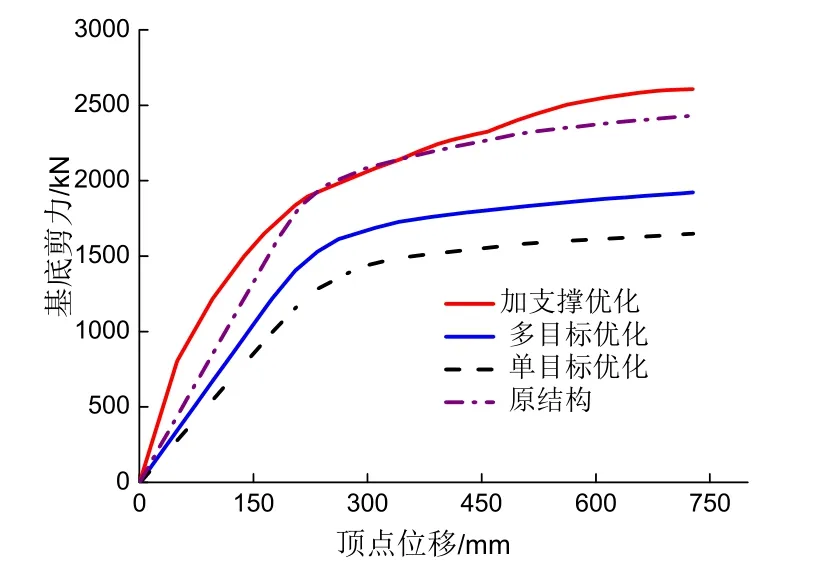
图3 Pushover结果Fig.3 Pushover results
在侧向力逐步施加的过程中,加支撑钢框架结构的出铰顺序大致为:上层支撑—三四层梁与柱变截面处—一二层梁与底部支撑.经过多目标优化后的钢框架的出铰顺序大致为:下部梁—下部柱—柱变截面处,说明设计均符合规范中“强柱弱梁”的原则.图中曲线近似由三段折线形成,第一段为弹性阶段;第二段由于塑性铰造成内力重分配,曲线突然变缓;第三段曲线斜率再次放缓,塑性铰逐步向极限状态发展.
5.2 结构层间位移
根据建筑场地类别和设计地震分组选用EL Centro波和Taft波对原结构和优化后的结构分别进行弹塑性时程分析,塑性铰的布置位置与推覆分析时相同,假定结构刚接于刚性基础上,结构在峰值加速度分别为70 gal和400 gal时对应的层间位移角如图4和图5所示:
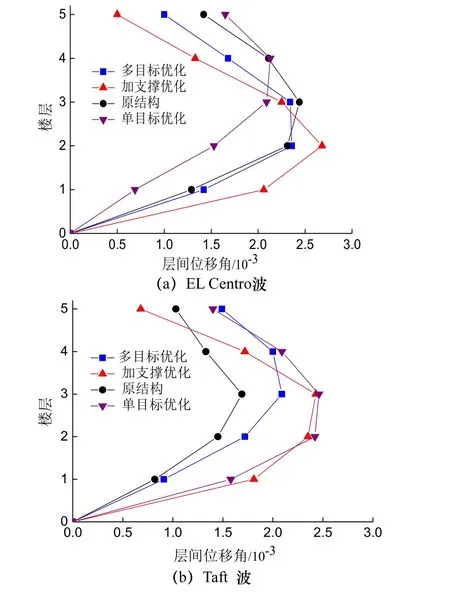
图4 峰值加速度分别为70gal时的结构层间位移角Fig.4 Drift ratio of the structure when the maximum input acceleration is 70gal

图5 峰值加速度分别为400 gal时的结构层间位移角Fig.5 Drift ratio of the structure when the maximum input acceleration is 400 gal
从图中可以看出,原结构和优化后结构在峰值加速度为70 gal的EL Centro波和Taft波作用下的最大层间位移角小于《建筑抗震设计规范》[7]多遇地震下弹性层间位移角限值1/250,在峰值加速度为400 gal的EL Centro波和Taft波作用下的最大层间位移角小于罕遇地震下弹塑性层间位移角限值1/50,但是单目标优化工况下钢框架在不同地震波作用下的层间位移角大小变化较大.在峰值加速度为70 gal的EL Centro波作用下,优化后结构的层间位移角与原结构差异不大;在峰值加速度为70 gal的Taft波作用下,多目标优化和加支撑优化下结构的层间位移角大于原结构,但小于单目标优化后结构.输入峰值加速度分别为400 gal的EL Centro波和Taft波作用后原结构不同位置均未出现塑性铰,表明其设计过于保守,由于在Taft波作用下,采用优化设计的结构发生破坏比在EL Centro波作用下严重,因此在图6中给出了峰值加速度为400 gal的Taft波作用下钢框架的出铰位置.

图6 峰值加速度为400 gal的Taft波作用下结构的出铰位置Fig.6 Plastic hinge position of different optimized structures when the maximum input acceleration of Taft wave is 400 gal
可以看出,增加支撑后单目标优化工况下,结构的梁和柱没有出现塑性铰,塑性铰基本集中在上层支撑上,而多目标优化工况下,钢框架仅在一、二层梁端局部出现塑性铰.
6 结论
(1) 合理选择设计变量的范围是优化结果是否准确的关键,为了实现“强柱弱梁”,规定梁截面的取值范围均不大于柱截面.
(2) 本文采用约束法用生成非劣解直观简单,易于使用,一般需要取较大的n值才能得到最佳均衡解,但是n值越大计算量也越大.
(3) 多目标优化后结构体积减小了16.7%,但在70 gal和400 gal的EL Centro波和Taft波分别作用下各层的层间位移角满足规范要求,其出铰数量和位置比单目标优化后的钢框架更为合理.
(4) 经拓扑分析增加支撑后,单目标优化得到的钢框架体积较原结构减小13.1%,框架—支撑体系在400 gal地震波作用下,上层支撑出现了大量塑性铰,造成上层的层间位移角较大,但从Pushover分析得到的结果可以看出其抗侧向荷载能力强于原结构.
(5) 单目标优化后的结构体积比原结构减小了26.3%,但是在不同地震波作用下的层间位移角大小波动较大,推覆分析中得到的基底剪力峰值比其他优化后的结构都小,输入峰值加速度为400 gal的地震波后结构的大部分梁和底部柱上均出现了塑性铰.
References
[1] 彭帅. 框架钢结构的研究及优化设计[D]. 武汉: 武汉理工大学, 2001.PENG Shuai. The research and optimization design of steel structure[D]. Wuhan: Wuhan University of Technology, 2001.
[2] CHAN C M, GRIERSON D E, SHERBOURNE A N.Automatic optimal design of tall steel building framework[J]. Journal of Structural Engineering, 1995, 121(5):838-847.
[3] 谢淮宁. 钢框架结构的优化设计研究[D]. 南京: 河海大学, 2006.XIE Huaining. Study on Optimal Design of Steel Frame Structure[D]. Nanjing: Hehai University, 2006.
[4] 李书全, 赵胜利, 冯利军. 遗传算法及其在水利土木工程中的应用[J]. 河北农业大学学报, 2002, 25(4):184-187.LI Shuquan, ZHAO Shengli, FENG Lijun. Genetic algo-rithm and its application in civil engineering[J]. Journal of Agricultural University of Hebei, 2002, 25(4): 184-187.
[5] KAVEH Ali, LAKNEJADI Karim, ALINEJAD Babak.Performance-based mul-ti-objective optimization of large steel structures[J]. 2012, 223(2): 355-369.
[6] GB50017-2003 钢结构设计规范[S]. 北京: 中国计划出版社, 2003.GB50017-2003 Code for design of steel struc-tures[S].Beijing: China Planning Press, 2003.
[7] GB50011-2010 建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2010.GB50011-2010 Code for seismic design of buildings[S].Beijing: China Architecture & Building Press, 2010.
[8] 方国华. 多目标决策理论、方法及其应用[M]. 北京:科学出版社, 2005.FANG Guohua. Multiple objective decision: theory, methods and applications[M]. Beijing: Science Press, 2005.
[9] 史祝. 大型火电厂主厂房钢框排架结构抗震性能试验及其优化设计[D]. 西安: 西安建筑科技大学, 2012.SHI Zhu. Experimental study on seimic behavior and the optimization designing about the steel frame-bent structure of the large-scale thermal power plant[D]. Xi'an:Xi'an University of Architecture And Technology, 2011.
[10] 陈绍蕃. 钢结构设计原理[M]. 3版. 北京;科学出版社,2005.CHEN Shaofan. Principle of Steel Structure Design[M].3rd ed. Beijing: Science Press, 2005.
[11] 胡聿贤. 地震工程学[M]. 北京: 地震出版社, 2006.HU Yuxian. Earthquake Engineering[M]. Beijing:Earth-quake Press, 2006.

