量子雷达技术发展与展望∗
(北京跟踪与通信技术研究所,北京100094)
0 引言
雷达是20世纪发明的用于目标探测和测距的远程传感设备,在军事与民用领域发挥了极其重要的作用,例如预警、监视、跟踪,天气预报、资源探测、环境监控以及天文观测等[1]。雷达通过发射电磁信号并接收目标反射回波信号可以感知并获取目标信息,如距离、速度、加速度等运动状态信息,通过深入信息处理可实现特征提取与目标识别、成像等任务需求。概率统计、控制论、信息论以及信号处理的应用不断促进雷达系统的完善以及性能的改良,但是经典雷达测量精度受限于客观物理规律而不能无限提升,因而不能满足日益苛刻的任务需求[2]。
在雷达技术于工程界得到极大发展的同时,物理学界构建了揭示自然世界客观规律的量子理论。利用量子现象可以完善经典信息系统,提升信息获取、传递与处理的性能与效率。在信息传递方面,利用单光子的BB84协议[3],利用量子纠缠的Ekert 91协议[4]以及BBM92协议[5]等量子密钥分布方案奠定了量子密码通信的基础[6]。在信息处理方面,Feynman在1982年提出量子计算的概念[7-8],Shor在1994年提出首个用于大数分解的量子算法[9];近来,利用多量子比特进行计算的量子计算机原型建造成功并能执行简单量子程序和计算。空间信息的获取主要通过远程传感器实现。远程传感即为对所接收的辐射信息进行检测、估计并重建空间目标及环境的过程,提升传感器灵敏度和分辨率是改善其信息获取能力的关键。为此,美国率先开展了利用量子纠缠等量子现象改进信息获取系统的理论与实验研究。在这方面,美国高等研究计划局(Defense Advanced Research Projects Agency,DARPA)于2007年组织领导了量子传感器项目(Quantum Sensor Program,QSP)[10],对量子激光雷达的增强技术进行探索研究,标志了量子远程探测领域的正式形成。此外,美国麻省理工、加州理工的JPL、NASA、海军实验室、空军实验室,以及其他多个研究机构均对相关领域进行了大量研究工作,极大地发挥了量子力学在信息获取系统中的威力。
量子雷达[11]是一种利用量子现象进行目标状态感知与信息获取的量子远程传感器。通过在发射端和(或)接收端引入量子增程策略,量子雷达的测量可以突破标准量子极限并逼近Heisenberg极限。本文将介绍量子雷达的基本概念原理和理论基础,对量子干涉测量、量子激光雷达以及量子照明的体制和性能进行介绍分析,并对量子雷达的技术要点和发展方向进行讨论与展望。
1 基本概念
经典雷达通过向目标发射电磁信号并接收目标调制的回波信号来实现测量。测量的精度(如距离、角度和速度等)信噪比,即其中SNR为信噪比。如果克服宏观误差因素的影响,诸如目标不确定性、大气抖动、设备系统误差等因素,经典雷达的信噪比极限SNR~N,N为信号中的探测到的平均光子数。由此,经典雷达的测量精度极限为由散粒噪声(Shot Noise)导致[12-13],称之为标准量子极限(Standard Quantum Limitation)。物理上散粒噪声由电磁场的离散本质和电磁波的泊松统计特性决定。
在微观世界,系统的行为诸如状态的演变无不遵循量子力学规律。而量子测量的极限则受限于量子世界的基本准则 —— 不确定性原理,称Heisenberg极限。如果在测量过程中采取一些策略,则测量灵敏度将有可能突破标准量子极限,并接近Heisenberg极限,即Δϕ~1/N。例如,在测量系统中引入高度关联的纠缠态、压缩态或者Fock态并对其进行协同测量。当测量的灵敏度优于标准量子极限并接近Heisenberg极限时,则称其为超灵敏测量[11],如图1所示。

图1 测量极限
2 量子雷达体制
通过在信号发射端和接收端引入量子增强策略,量子增强策略通过量子发射机和量子接收机实现,可以改善系统的探测性能,经典雷达与量子雷达基本示意如图2所示。根据增强策略可将量子雷达系统分为3类:第1类,发射非经典态作为探测信号,无本地态与发射信号相互纠缠,如N00N态干涉测量(Quantum Interferometry);第2类,发射经典态作为探测信号,在接收端采用非经典探测技术,如基于压缩态注入和相位敏感放大的量子激光雷达系统(Quantum LADAR);第3类,本地态与发射态相互纠缠,利用发射信号与本地信号的纠缠特性提高检测性能,如量子照明系统(Quantum Illumination)。

图2 经典雷达与量子雷达基本示意
2.1 量子干涉测量
量子干涉测量可抽象成Mach-Zender干涉仪模型[11],采用N00N态作为发射信号,能够突破标准量子极限达到Heisenberg极限。N00N态两光子分别在干涉仪两臂中传播,由于两臂的等效长度的差异,N00N态中引入了相位延迟ϕ,并兼顾量子力学中产生算符和湮灭算符的影响,选择观测量,可得到测量相位误差达到Heisenberg极限。而对于经典可分离态而言,有相位误差极限未突破标准量子极限。
考虑N00 N态在衰减介质中的传播[14],量子干涉仪模型中的一个路径长度可以等效于0,于是得到简化的测量相位误差极限,δϕD=其中α=exp(-χL),χ为衰减系数,L为在传播介质中传播的距离。大气衰减趋于0即α趋于1时,δϕD回归Heisenberg极限,δϕS回归标准量子极限,然而δϕS相比于δϕD随α增加趋势更为平缓,即相干测量在衰减介质中性能更容易弱化。令δϕD= δϕS,可得(N-1)αN+NαN-1=1,方程具有唯一解α∗,随N增加而递减,定义为临界透射常数,表示相干测量性能与非相干测量性能相等时的透射率。当超过临界透射常数时,相干测量的灵敏度将弱于非相干测量。令可得(2N-1)αN=1,方程具有唯一解α+=(2N-1)-1/N,定义为超灵敏透射极限,表示当α超过α+,相干测量由于透射率的减弱而无法实现超灵敏测量。α∗与α+随N增加而增大,如图3所示。
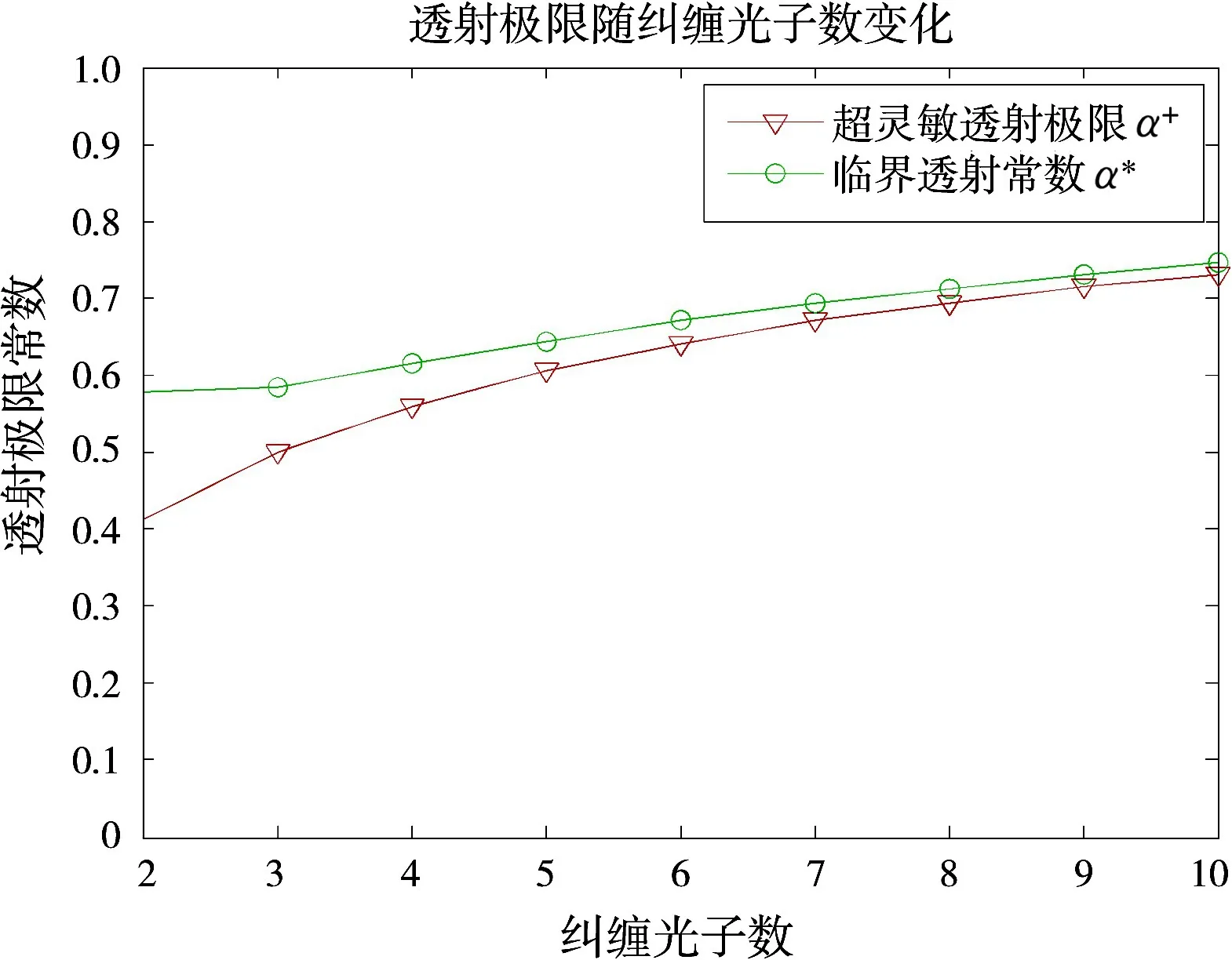
图3 量子干涉测量介质透射极限
对于N=2双光子情形,超灵敏透射极限α+=0.414,临界透射常数α∗=0.577,可得超灵敏测量极限距离与相干最优测量临界距离分别为L+=-ln(α+)/χ,和L∗=-ln(α∗)/χ。对于X波段信号,波长λ=3.2 cm时,当能见度为300 m时,等效衰减系数χ=0.0016/km。
基于N00N态的量子相干测量可以突破标准量子极限,然而其性能在衰减介质中减弱明显,不利于实际测量。此外,纠缠态对衰减介质的敏感性强于非纠缠态,因而当超过临界透射常数时,纠缠态的测量相比非纠缠态将不再具备优势,如图4所示[11,14]。量子干涉雷达是一类原理上可以应用于实际的超灵敏雷达。在衰减介质中,量子干涉测量的性能随透射率降低而衰减,将此原理应用于大气可以得到量子干涉雷达在实际应用中的超灵敏距离。
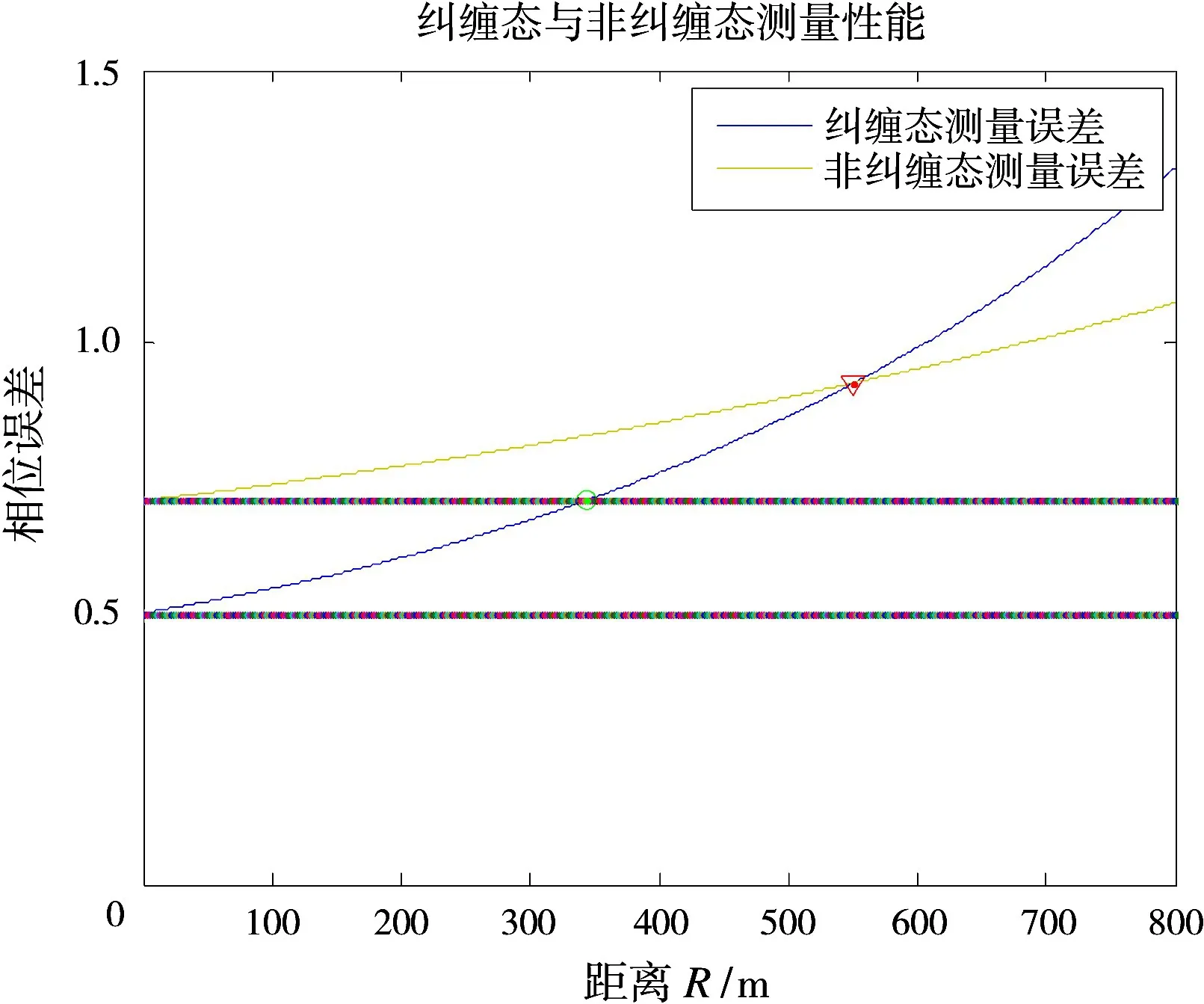
图4 衰减介质中量子干涉测量性能
2.2 量子激光雷达
LADAR是利用激光作为探测波束的雷达系统。在DARPA的QSP项目[10]以及后续研究中, MIT、Raytheon公司和Harris公司等研究机构将利用压缩真空注射(Squeezed Vacuum Injection, SVI)和相位敏感放大(Phase-Sensitive Amplification,PSA)[15]的零差检测(Homodyne)技术引入激光雷达系统接收机中,实现了空间分辨率的提高与突破,如图5所示[10,16]。SVI和PSA作为利用量子现象的操作方法,联合作用有效降低了激光雷达接收端噪声本底,可大幅提升系统角度[16]和距离[17]分辨率。

式中,P为探测系统的噪声功率谱密度[10],Geff为PSA增益,r为压缩真空参数,1-η为零差检测效率。其中各项分别表示由目标回波、真空压缩和零差检测引入的量子噪声。当Geff=1,r=0时,噪声回归为基本激光雷达检测系统,等效于SVI和PSA无作用;当r>0,SVI的作用使得目标的高空间频率细节信息引发的量子噪声被有效抑制;当Geff>1时,PSA的作用使得零差检测的噪声影响被降低。因而,SVI和PSA的联合作用成功抑制激光雷达接收端的量子噪声,实现检测性能的大幅增强。量子激光雷达由于在接收机采用量子增强技术,无需非经典信号的使用,对信号源的限制得到有效降低。
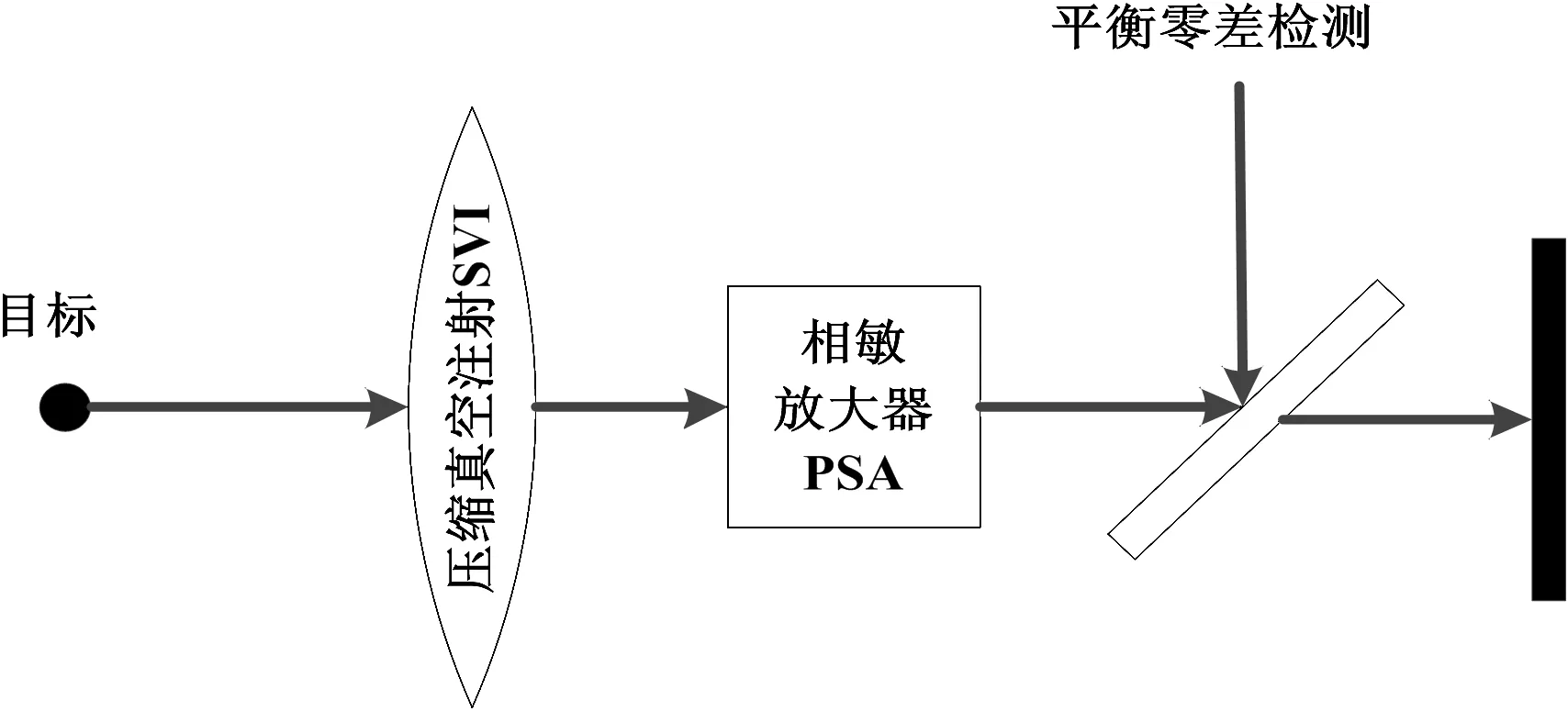
图5 SVI和PSA量子增强技术
2.3 量子照明
传统的雷达系统向空间目标发射经典电磁信号并接收散射回波实现探测;量子干涉测量等第1类量子雷达通过发射非经典信号实现探测;量子激光雷达等第2类量子雷达通过在接收机端引入增强策略实现检测性能的提升;此外,仍可利用纠缠信号进行目标探测,如量子照明。量子照明(Quantum illumination)[18]是MIT的Lloyd于2008年提出的目标探测方案,适用于高介质损耗和强噪声背景的情形。如图6所示,量子照明方案利用纠缠源对目标进行照射,纠缠信号一部分作为本地信号储存,另一部分作为发射信号进行目标探测,在接收端对本地信号和目标散射信号联合测量,从而实现探测灵敏度的提高。Lloyd的理论研究表明,相比于传统光源,m量子比特的纠缠信号可实现2m倍探测信噪比的提升,在损耗强噪声情况下同样具有高灵敏的检测性能,并且适用于任何信号频率。2012年,意大利首次在实验上实现了量子照明方案[19]。实验中,β-BBO晶体作为纠缠源,一部分光束直接发射到探测装置,另一部分经目标散射到探测装置,在散射光束中加入热源噪声,探测装置实现了量子照明方案中的高灵敏信号检测,证实了其在实际工程应用中的可行性。此外,CIT、MIT等研究机构提出了适用于量子照明的接收机方案,可实现信号的优化检测[20-21]。量子照明由于在损耗和噪声环境下的适用性而具有可观的实际应用前景。

图6 量子照明示意图
3 量子雷达关键技术
雷达的量子增强策略在理论上是可行的,但是从概念到量子雷达系统实现的推进仍需大量研究。量子照明是最典型、最具前景的量子雷达,发展量子照明体制涉及诸多技术,如非经典信号源的研制、量子信号的调制机制、量子信号的探测器件等,本节对这些关键技术着重展开讨论。
3.1 量子纠缠源
在量子干涉测量与量子照明等多数量子测量体制中,系统通过引入非经典信号实现探测性能的增强,其中纠缠是最成熟的非经典信号。目前已报道的量子纠缠产生方法包含原子纠缠(腔量子电动力学)、离子纠缠(离子井)和原子核纠缠(核磁共振)等多种可能,然而由于这些纠缠形态无法在自由空间中有效传播,光子纠缠成为适用于量子雷达优化的选择。纠缠光子的产生也有多种可行方法。利用正负电子湮灭产生γ纠缠对是产生光子纠缠态的最早报道;电磁振荡、原子核中电子跃迁以及原子核内能级跃迁是产生各波段纠缠光子的有效途径。纠缠光子的制备通常利用非线性晶体中的三波混频过程、光纤中的四波混频过程、半导体器件中的四波混频过程等方式实现。三波混频是在β硼酸钡(BBO)、周期性极化钛氧基磷酸钾和铌酸锂等晶体中,泵浦光子通过自发参量降频转换效应(Spontaneous Parametric Down Conversion,SPDC)分解成较低能量的纠缠光子对[22],可产生极化、动量、角动量等多种纠缠方式,转换效率依赖于晶体类型。自发四波混频过程(Spontaneous Four-Wave Mixing,SFWM)主要发生在标准光导纤维和光子晶体纤维中[23-24],在SFWM过程中,两个泵浦光子被转化成纠缠光子对,其频率仍保持在相同波段。此外, SFWM也可发生在微纳波导与谐振器等Si、SiN半导体器件中。半导体纠缠源更容易整合到芯片等精密部件中。高效、稳健的量子纠缠源为量子雷达的构建奠定了基础保障。
3.2 非经典信号的调制
传统雷达回波为发射电磁波在空间环境背景下与目标共同作用的结果,环境作用包含噪声、干扰和杂波等,目标的调制由材料、形状、姿态和运动等因素决定,可用Maxwell方程组、本构方程以及边界条件完全刻画。目标调制的物理过程可表现为振荡电磁场照射目标产生表面电流,表面电流激发空间散射电磁场形成回波信号;散射场的畸变或其他成分电磁场的叠加即表现为环境作用。关于目标与环境对非经典信号(如纠缠光子)调制的研究尚不成熟。非经典信号载体多以少数光子形式存在,与目标及环境的相互作用可表征为光子和原子的散射作用,需由描述电磁场与带电粒子相互作用的量子电动力学刻画,调制机制依赖于微观电磁作用的量子特性,不再适用于揭示宏观电磁波动特性的Maxwell方程。纠缠信号调制的物理内涵在于,运动目标的原子与之相互作用对探测光子的属性改变以及对光子纠缠特性的影响,然而这些基本物理过程均需要深入探索研究。
3.3 非经典信号的检测
纠缠信号检测的核心内容是单光子探测和纠缠检测。单光子探测广泛应用于光子计数成像领域,信号微弱到以离散光子的形式存在,是微弱信号检测的极端情况。对于纠缠光子的探测,可使用单光子探测技术。光电倍增管和雪崩光电二极管等单光子探测器为纠缠光子的检测提供了可能;近年来发展起来的超导探测器在单光子检测方面同样具有可观的潜力。此外,纠缠光子对在大气中会发生退相干效应,同样会受目标调制作用的影响,量子纠缠态的测量则需要用Bell型CHSH不等式来验证。
4 智能量子照明系统结构构想
与传统雷达相比,量子照明系统虽具有相似的基本结构,但是却有截然不同的模块。纠缠源产生的双光子纠缠信号由分发器分两路传送至存储器和双工器,双工器与天线的作用同传统雷达,双工器接收的回波信号与存储器中信号同时传送至纠缠信号检测器,随后进行信号与数据处理。为了增强量子雷达的性能,借鉴认知雷达思想,在量子雷达系统中增加两个改进举措,即引入从接收机到发射机的信息反馈回路和知识辅助控制管理系统。一方面,信息反馈回路由自适应纠缠源和自适应信号与数据处理系统构成,接收机端向发射机端提供关于目标的信息反馈,以便纠缠源调整信号参数,从而提高接收机获取目标信息效率;另一方面,控制管理系统作为智能处理中枢,根据专家准则以及实时更新的目标、环境数据库提供的先验信息进行决策、目标分析和发射信号优化等。由此构成智能化量子雷达系统,如图7所示。
5 结束语
物理规律客观约束测量系统精度的无限提升,理论上雷达系统通过引入基于量子现象和量子技术的增强策略可以突破标准量子极限达到Heisenberg极限。量子干涉测量、量子激光雷达和量子照明技术等是很有前景的量子雷达。量子雷达的前景尽管十分可观,但是目前的发展面临众多亟待解决的问题与瓶颈。在理论上,目标对纠缠态的调制作用、发射信号的最佳信号形式、接收信号的检测与估计理论、信号的衰减、噪声等,尚属空白;实验上,量子雷达模拟平台需要合适的纠缠源与可行的检测方法;所有适用于目标探测的量子雷达模块及部件开发仍需更长远且持久、深入的研究。

图7 智能化量子照明系统构想
[1]胡飞,崔国龙,孔令讲.雷达-通信一体化网络设计[J].雷达科学与技术,2014,12(5):455-459,469.
[2]韩国强,叶瑞芳,刘丽,等.对新型ISAR欺骗干扰效果仿真分析[J].雷达科学与技术,2014,12(5):532-538.
[3]BENNETT C H,BRASSARD G.Quantum Cryptography:Public Key Distribution and Coin Tossing[C]∥IEEE International Conference on Computers,Systems and Signal Processing,New York:IEEE,1984:175-179.
[4]EKERT A K.Quantum Cryptography Based on Bell’s Theorem[J].Physical Review Letters,1991,67(6): 661-663.
[5]BENNETT C H,BRASSARD G,MERMIN N D. Quantum Cryptography Without Bell’s Theorem[J]. Physical Review Letters,1992,68(5):557-559.
[6]NIELSEN M A,CHUANG I L.Quantum Computation and Quantum Information[M].London:Cambridge University Press,2010.
[7]FEYNMAN R P.Simulating Physics with Computers [J].International Journal of Theoretical Physics, 1982,21(6-7):467-488.
[8]FEYNMAN R P.Quantum Mechanical Computers [J].Foundations of Physics,1986,16(6):507-531.
[9]SHOR P W.Algorithms for Quantum Computation: Discrete Logarithms and Factoring[C]∥35th Annual Symposium on Foundations of Computer Science, LOS Alamitos,CA,USA:IEEE,1994:124-134.
[10]BURDGE G,DEIBNER G,SHAPRIO J,et al. Quantum Sensors Program[R].Rome,NY:AFRL/ RITC,2009.
[11]LANZAGORTA M.Quantum Radar[J].Synthesis Lectures on Quantum Computing,2011,3(1):1-139.
[12]XIAO M,WU L,KIMBLE H J.Precision Measurement Beyond the Shot-Noise Limit[J].Physical Review Letters,1987,59(3):278-281.
[13]GIOVANNETTI V,LLOYD S,MACCONE L. Quantum-Enhanced Measurements:Beating the Standard Quantum Limit[J].Science,2004,306 (5700):1330-1336.
[14]SMITH III J F.Quantum Entangled Radar Theory and a Correction Method for the Effects of the Atmosphere on Entanglement[J].Proceedings of the SPIE,Quantum Information and Computation VII, 2009,7342(73420A):1-12.
[15]WASILOUSKY P A,SMITH K H,GLASSER R, et al.Quantum Enhancement of a Coherent Ladar Receiver Using Phase-Sensitive Amplification[J].Proceedings of the SPIE,Quantum Communications and Quantum Imaging IX,2011,8163(816305):1-15.
[16]DUTTON Z,SHAPIRO J H,GUHA S.LADAR Resolution Improvement Using Receivers Enhanced with Squeezed-Vacuum Injection and Phase-Sensitive Amplification[J].Journal of the Optical Society of America B: Optical Physics,2010,27(6):A63-A72.
[17]NAIR R,YEN B J,SHAPIRO J H,et al.Quantum-Enhanced Ladar Ranging with Squeezed-Vacuum Injection,Phase-Sensitive Amplification,and Slow Photodetectors[J].Proceedings of the SPIE, Quantum Communications and Quantum Imaging IX,2011,8163(816310):1-14.
[18]LLOYD S.Enhanced Sensitivity of Photodetection via Quantum Illumination[J].Science,2008,321 (5895):1463-1465.
[19]LOPAEVA E,BERCHERA I R,DEGIOVANNI I, et al.Experimental Realization of Quantum Illumination[J].Physical Review Letters,2013,110(15): 153603(1-5).
[20]GUHA S,ERKMEN B I.Gaussian-State Quantum-Illumination Receivers for Target Detection[J]. Physical Review A,2009,80(5):052310(1-5).
[21]TAN S,ERKMEN B I,GIOVANNETTI V,et al. Quantum Illumination with Gaussian States[J].Physical Review Letters,2008,101(25):253601(1-4).
[22]KITAEVA G K,PENIN A N.Spontaneous Parametric Down-Conversion[J].Journal of Experimental and Theoretical Physics Letters,2005,82(6):350-355.
[23]TAKESUE H,INOUE K.Generation of Polarization-Entangled Photon Pairs and Violation of Bell’s Inequality Using Spontaneous Four-Wave Mixing in a Fiber Loop[J].Physical Review A,2004,70(3): 031802(1-11).
[24]GARAY-PALMETT K,MCGUINNESS H J,COHEN O,et al.Photon Pair-State Preparation with Tailored Spectral Properties by Spontaneous Four-Wave Mixing in Photonic-Crystal Fiber[J].Optics Express,2007,15(22):14870-14886.

