“一步一停”假设不成立时的星载聚束SAR成像∗
(中国电子科技集团公司第三十八研究所,安徽合肥230088)
0 引言
随着星载SAR技术的不断发展[1],星载SAR图像的分辨率也在不断提高。从最初Seasat-A几十米的分辨率,到现在美国长曲棍球(Lacrosse)军事侦察卫星0.3 m的分辨率,而试验中的Terra-SAR-X凝视聚束模式(Staring Spotlight,SL)的方位分辨率已经达到了0.2 m[2]。未来的星载SAR很可能达到0.1 m或更高的分辨率,最有可能获得如此高分辨率的成像模式是聚束SAR。对于这种超高分辨率聚束SAR成像,有两个问题需要解决。首先,此时的合成孔径长达几百公里,常规的直线飞行轨迹模型已不再满足要求,必须考虑轨道曲率的影响,亦即传统星载SAR成像所使用的等效距离模型在这种条件下已不再适用。其次,对于星载超高分辨率SAR成像,回波模型中传统的“一步一停”假设不再成立。如果此时还采用传统的成像算法,目标的聚焦效果将无法达到系统的要求。
对于第一个问题,已陆续有文献提出了解决方法,主要是提高距离模型的阶数[3-4],同时辅以模型参数的方位时变校正[5]。对于这个问题,这里不过多涉及,本文重点讨论第二个问题,亦即“一步一停”假设不成立或平台连续运动时星载超高分辨率SAR的成像。其实,在调频连续波SAR成像中必须要考虑平台的连续运动,但在传统SAR成像领域,在已公开的文献中较少涉及这个问题。文献[6]首次提出了在0.1 m星载SAR回波中“一步一停”假设不成立时对点目标压缩的影响,并给出了仿真结果。在TerraSAR-X凝视聚束成像过程中,也特别校正了轨道曲率以及“一步一停”假设不成立的影响[7]。文献[8]提出了在二维频域补偿上述误差的方法。文献[9-10]较为系统地分析了“一步一停”假设不成立对成像的影响,并在直接推导回波信号二维频谱的基础上提出了星载聚束SAR成像的方法。而本文补偿了“一步一停”假设不成立所造成的信号畸变,基于该假设成立条件下的点目标的二维频谱,并结合Chirp-Z变换,提出了另一种较为简便的超高分辨率星载聚束SAR成像算法。该算法的有效性通过仿真实验得到了验证。
1 星载SAR精确回波模型
目前,SAR信号的处理和分析都是基于“一步一停”假设,该假设忽略了两种雷达运动,一种是发射和接收期间的雷达运动,另一种是信号传输期间的雷达运动。通常情况下该假设都是成立的,这给SAR理论分析带来了很大的便利。但是,在雷达运动速度很大,且成像的方位分辨率很高时,回波信号畸变可忽略的判别依据[11]不再成立。
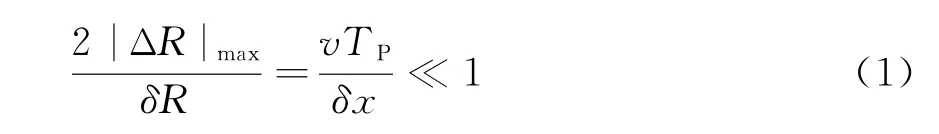
式中:|ΔR|max为“一步一停”假设成立与否时目标回波延迟距离的最大差异;v为卫星速度;TP为脉冲宽度;δR,δx分别为距离和方位向的分辨率。此时,必须考虑回波信号的畸变,否则会严重影响目标的压缩质量。
图1为考虑雷达连续运动时雷达信号从发射到接收的时间示意图,信号从发射到接收的时延可以看作是信号从发射到目标的传输时间与从目标到接收的传输时间之和。脉冲发射时刻卫星的坐标位置为,其中,为距离快时间,且为方位慢时间。发射路径上电磁波传播的延迟为τ1,接收路径的延迟为τ2,总的延时τ=τ1+τ2。那么,脉冲接收时刻)卫星的位置为且若地面目标的坐标为(xP,yP,zP),则有
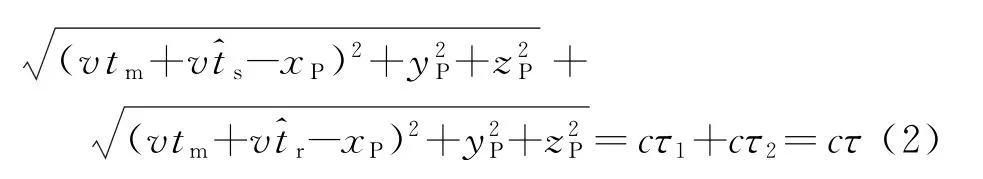
式中,c为光速。整理式(2),可得总的延时:
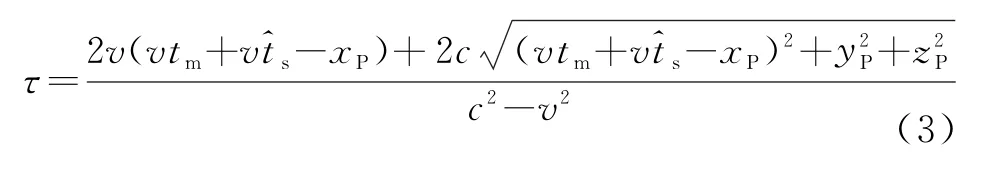
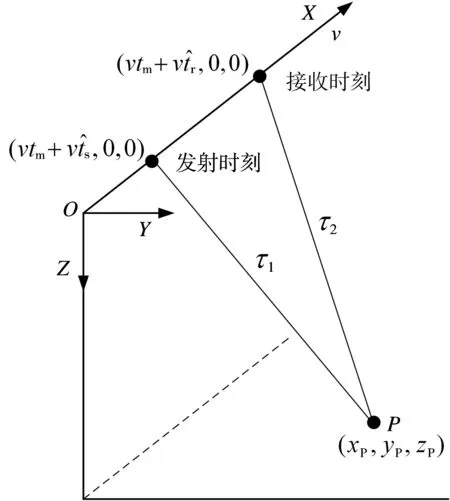
图1 卫星发射和接收回波示意图
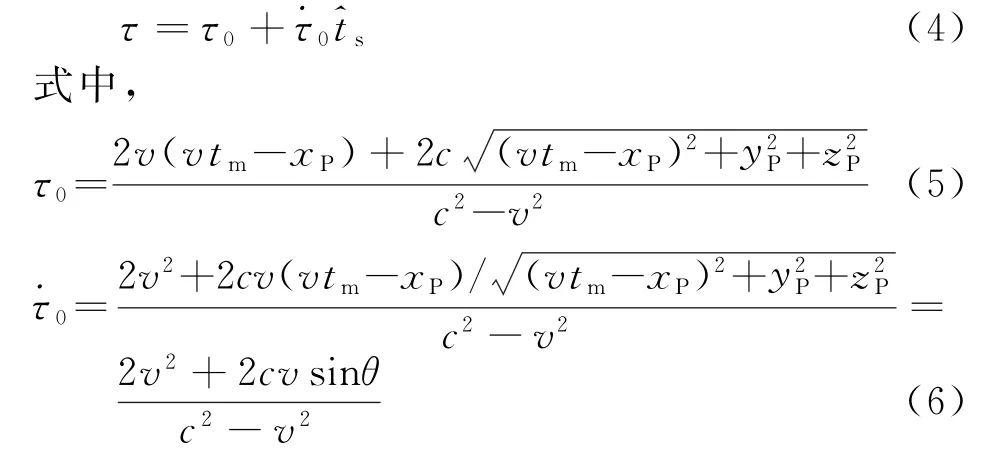
式中,θ为目标的瞬时斜视角。根据式(4)有
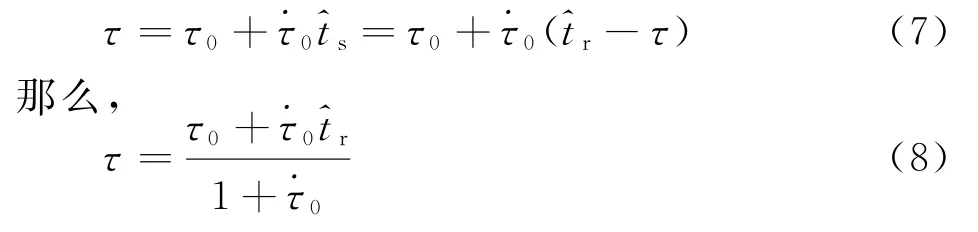
所以,可以根据脉冲接收的距离向时间来计算回波的准确延时。
假设发射脉冲为线性调频信号:
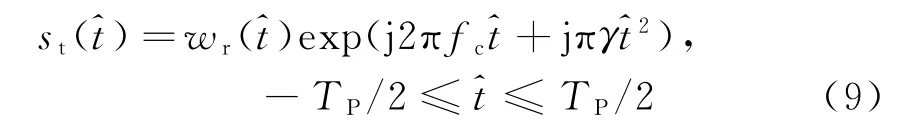
式中,wr(·)为发射脉冲的包络,fc为发射电磁波的中心频率,γ为发射信号的调频率。那么,点目标回波信号为
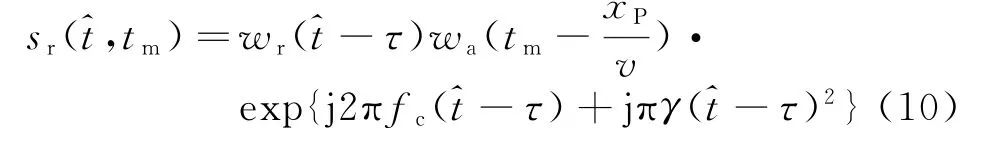
式中,wa(·)为方位向天线方向图。式(8)中的r可以用替换,表示距离向时间。那么,将式(8)代入式(10)得到
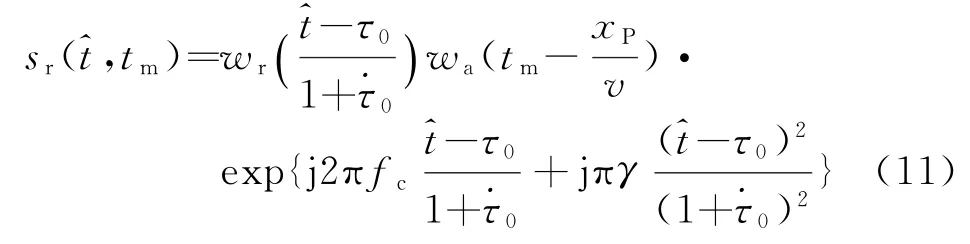
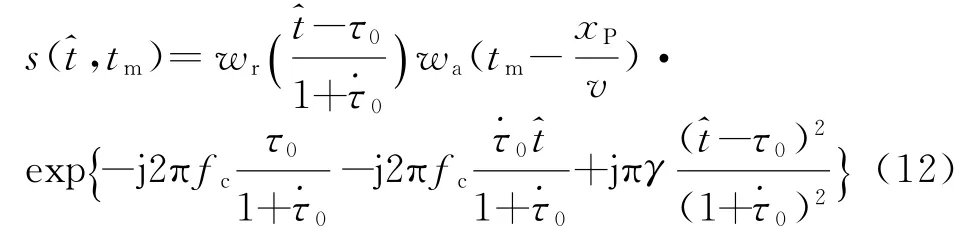
式(12)就是考虑了“一步一停”假设不成立时的回波信号。可以看出,该回波的相位中除了二次相位,还存在由于正交解调而剩下的线性相位,且二次相位的调频率变为该调频率随平台和目标间的瞬时斜视角的改变而改变。
2 改进的聚束SAR成像方法
2.1 “一步一停”假设不成立时的频谱
利用驻定相位原理,对式(12)进行距离向FFT,有
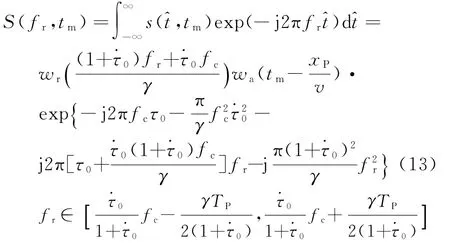
式(13)中,等式右边相位的第一、二项为距离频率的常数项,在进行距离压缩时可以不予考虑。第三项是距离向频率的一次函数,在距离压缩时将造成目标位置的位移。此时,压缩后的目标距离向位置位于处。第四项是距离频率的二次项,用于目标压缩。式(6)中不仅与平台的方位位置有关,还与目标所处的位置有关。也就是说,对于不同的点目标,用于目标压缩的距离向调频率都是不同的。这对快速成像处理很不利。而聚束SAR成像的场景范围较小,可以利用位于场景中心的目标位置计算所得的距离调频率作为全场景的距离调频率,即此时的距离向脉压函数变为为场景中心位置处计算的值。这种近似引起的聚束SAR全场景范围内的二次相位误差(QPE)[12]:
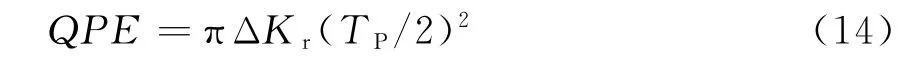

表1 聚束SAR仿真系统参数
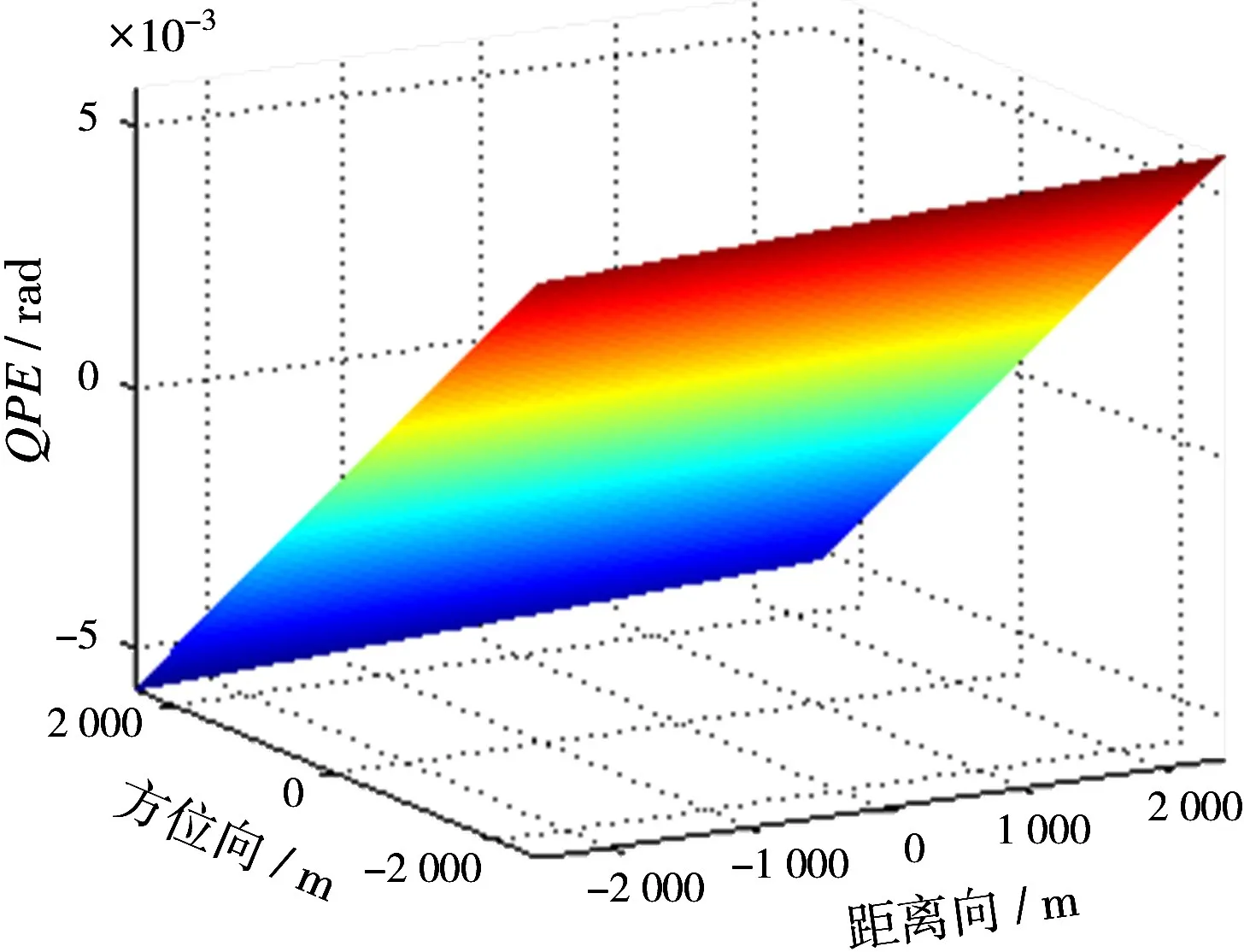
图2 距离向调频率近似引起的全场景范围内的QPE值
利用上述距离向压缩的方法,可以将式(13)中距离向频率的二次项消除掉,亦即进行距离压缩后的信号在距离向频域的形式为
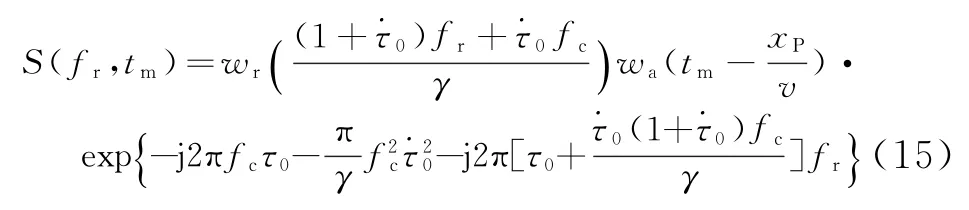
对于式(15),如果认为τ0是目标的延时,那么相位中的是多余的项,需要进行补偿。根据̇τ0的计算公式及一般的超高分辨率星载聚束SAR参数,的值非常小,可以忽略不计。而项与目标的距离徙动有关,相对于τ0,残余的徙动量为由于与目标的位置和平台的方位位置都有关,所以该徙动量是方位时变和距离空变的量。对于聚束SAR场景中心的目标,利用表1计算的残余的距离徙动量如图3所示。对于方位向±3°的旋转角,中心目标的最大残余距离徙动量不超过±3 cm。对于分辨率为0.1 m左右的SAR系统,需要补偿该距离徙动量。对于全场景中的目标,它们与中心目标残余徙动量的典型差异如图4所示。对于表1中的参数,通过计算可以看到,利用中心目标的残余徙动量对全场景范围内的目标进行补偿,引起的最大误差不超过±2 mm,且该误差与目标方位位置强相关、与目标距离位置弱相关。对于分辨率为0.1 m左右的SAR系统,2 mm的距离徙动误差对方位和距离向脉压的影响很小,可以不用补偿。
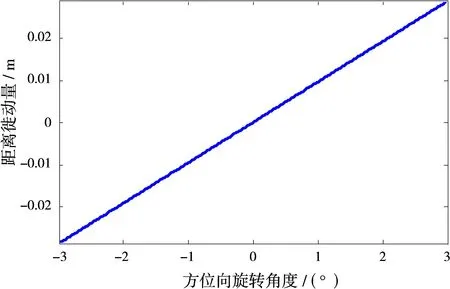
图3 聚束SAR场景中心目标的残余距离徙动量随方位变化的情况
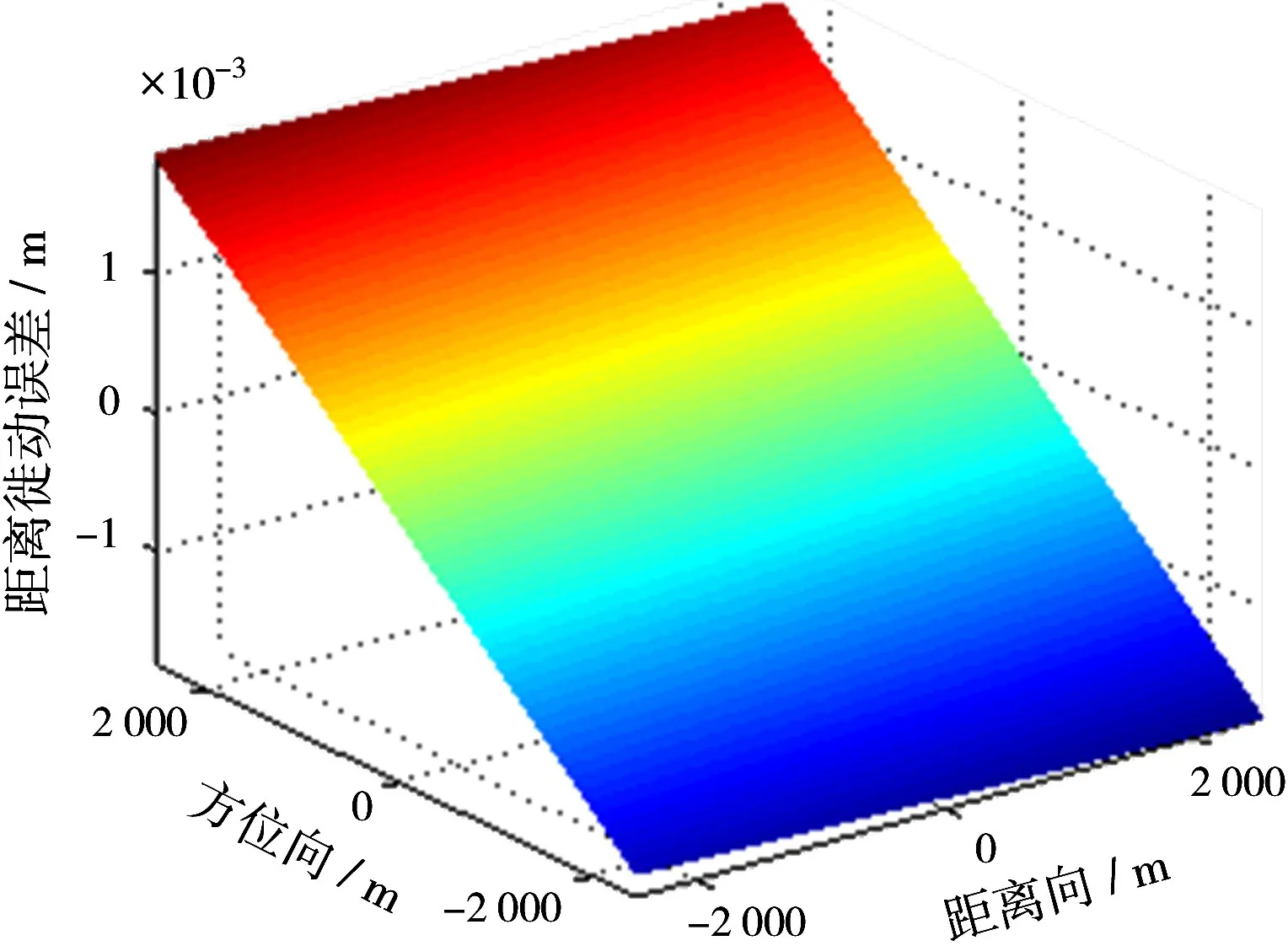
图4 全场景范围内的目标与中心目标残余距离徙动量的典型差异
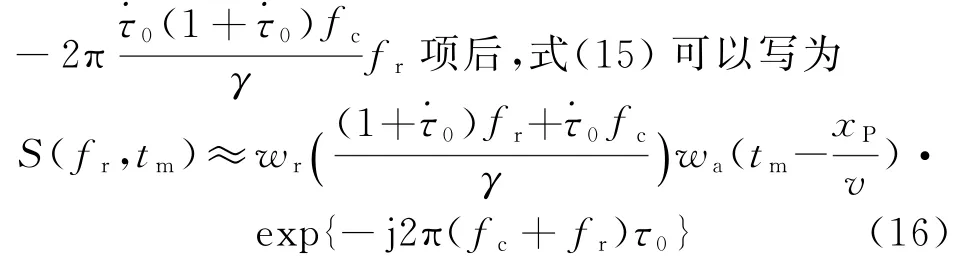
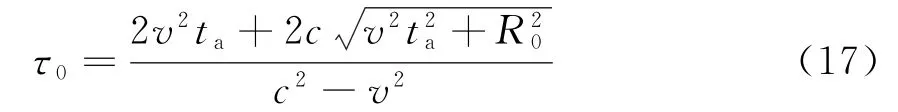
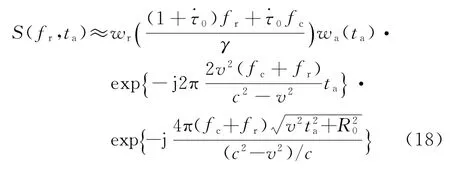
观察式(18)可知,该式中的第二个指数项除了将光速c替换成(c2-v2)/c外,其信号形式与“一步一停”假设成立条件下的目标方位信号完全一致[12],因此,根据文献[12]的方位向傅里叶变换可以很容易地写出
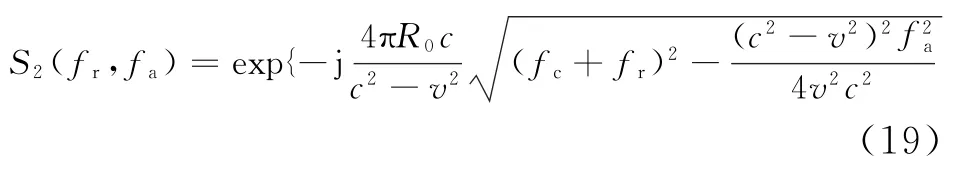
由于式(18)中第一个指数项的相位是方位时间的线性函数,根据傅里叶变换的性质,信号在时域乘以一个线性相位函数等效于在频域进行相应的频谱位移。因此,根据式(19)也可以方便地写出式(18)的方位向傅里叶变换形式:
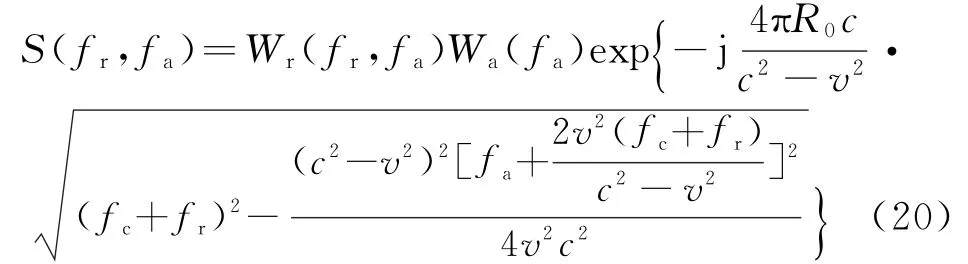
式中,Wa(fa)为wa(ta)的频域形式,Wr(fr,fa)=式(20)就是距离压缩和额外距离徙动校正之后的点目标二维频谱。
2.2 完整的聚束SAR成像流程
在使用频域算法进行聚束SAR成像时,会存在方位向频谱混叠的情况,因而在进行成像之前必须进行方位向频谱去混叠处理。这里,利用Lanari等人提出的“两步成像”方法进行聚束SAR成像[13]。首先,利用SPECAN技术的思想,通过时域卷积的方法去除方位向频谱混叠;随后,利用成熟的条带SAR成像算法进行处理,这里使用ω-k算法。
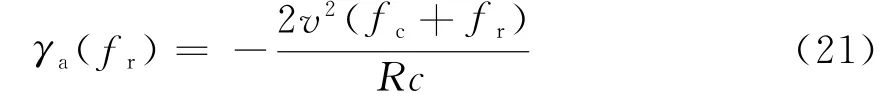
对于常规的SAR成像,原始回波信号的方位调频率为可以看出,方位调频率γa(fr)与距离频率fr正相关,但Lanari等人的方法中没有考虑方位调频率随fr变化的情况[13]。而对于星载超高分辨率聚束SAR,距离向带宽非常大,在距离向高频段,方位调频率太大仍足以造成方位模糊[14]。可以通过提高方位向脉冲重复频率的方法消除该模糊[14],也可以在去方位频谱混叠时,考虑方位调频率随距离频率的变化,即此时的去斜函数[9]为
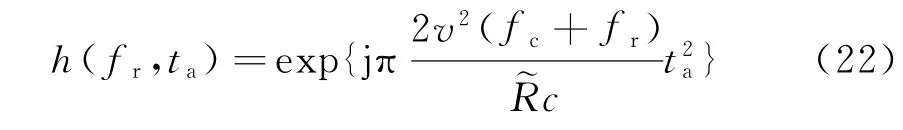
式中,~R为去斜函数的参考斜距。这里,本文采用第二种方法,通过信号与去斜函数h(fr,ta)的卷积,消除距离向宽带引起的方位模糊。
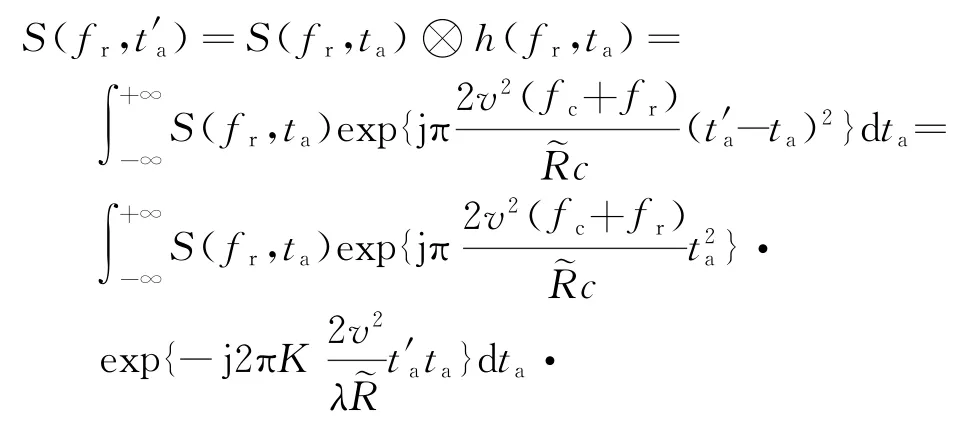
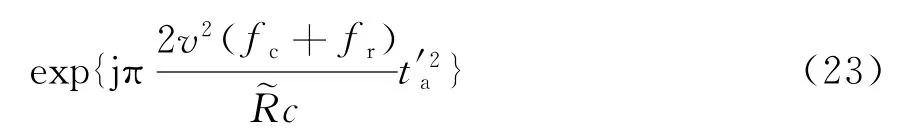
式中,K=1+fr/fc,t′a为去斜后的方位向时间。需满足以下关系式:
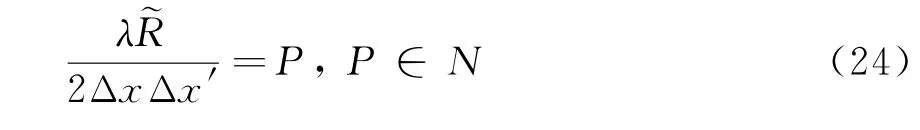
式中,Δx,Δx′分别为原始的和去斜后的方位向采样间隔,P为去斜后的方位向采样点数。由于存在系数K,上述积分变成变标傅里叶变换(SCFT)。这里,本文利用Chirp-Z变换高效实现SCFT[12],再补偿由去斜造成的残余相位,就可以消除方位向的频谱混叠。
方位频谱混叠消除之后,就可以利用ω-k算法进行成像了。根据式(20)所示的点目标二维频谱,其匹配滤波函数为
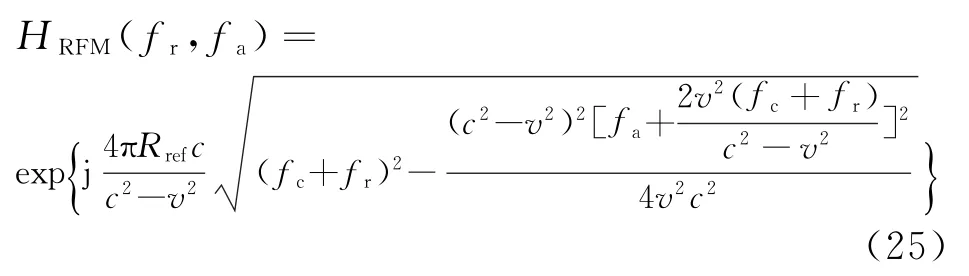
式中,Rref为ω-k成像算法的参考距离。经过匹配滤波处理后,参考距离处的相位能够完全补偿,而其他距离处的目标则存在残余相位。对全场景进行剩余聚焦时,将原来的频率轴fr映射为新的频率轴f′r,即解此一元二次方程,得到fr的表达式,然后利用Stolt插值就可完成成像。
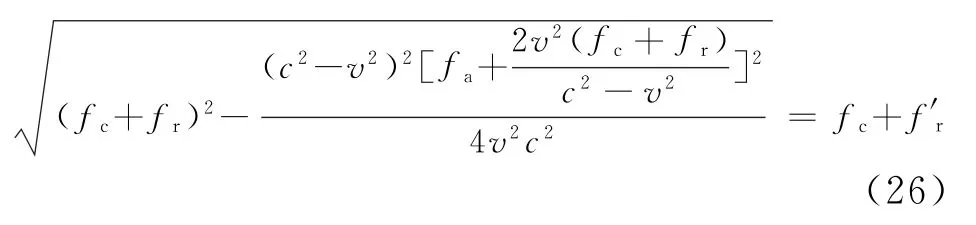
根据以上论述,“一步一停”假设不成立时,完整的星载聚束SAR成像的流程如图5所示。从图中看出,在“两步成像”的基础上,针对“一步一停”假设不成立的情况,增加了额外距离徙动校正的步骤,修改了距离向压缩的表达式,并将原来的参考函数中的光速c和方位频率分别进行了替换。而修改后的距离压缩几乎不增加运算量,因此,与“一步一停”假设成立时的“两步成像”算法相比,修改后的星载聚束SAR成像算法只增加了一次相位相乘、两次变量替换的运算,计算量的增加很少,可以对传统的“两步成像”算法进行很小的调整就可以完成整个成像过程。
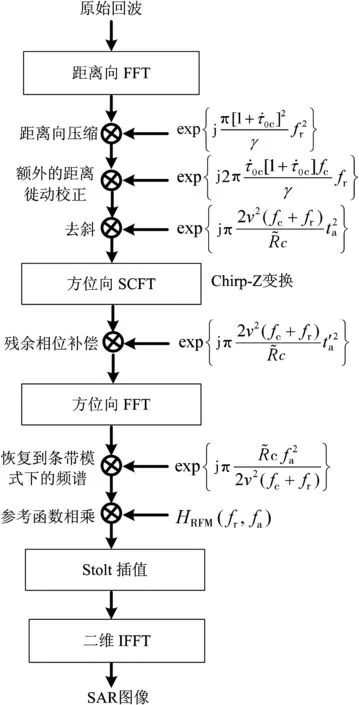
图5 “一步一停”假设不成立时星载聚束SAR“两步成像”的流程图
3 仿真试验
为了验证本文算法的有效性,利用表1中的参数对位于场景中的9个点目标进行成像。点目标的分布位置如图6所示,坐标为(0,R0)的目标位于场景的中心。成像过程中均未加窗,点目标的理论方位分辨率约为0.149 m。图7(a)是利用常规的基于ω-k算法的“两步成像”方法得到的聚束SAR成像结果;图7(b)是本文算法得到的聚束SAR成像结果;图7(c)是本文成像方法的距离向点目标响应;图7(d)是本文成像方法的方位向点目标响应。图8(a)、(b)分别是它们的方位向点目标响应和距离向点目标响应。图中只列出了场景中心处和(2500,R0+2500)处的点目标压缩图,其他位置也有类似结果,这里没有一一给出。可以看到,在“一步一停”假设不成立时,利用常规的聚束SAR成像方法进行压缩,方位向分辨率降低,旁瓣升高,且峰值两端的信号很不对称,距离向旁瓣退化,点目标的整体压缩质量严重恶化。而且,压缩后的点目标方位位置整体偏移了194个像元,约19 m。而利用本文算法,即补偿了“一步一停”假设不成立所造成的信号畸变后,点目标压缩质量得到了极大提高,目标也成像在正确的方位位置上。表2列出了利用本文算法成像后9个点目标在距离向和方位向的分辨率、峰值旁瓣比(PSLR)和积分旁瓣比(ISLR)。

图6 场景中的点目标在斜距平面上的分布图(坐标单位:m)
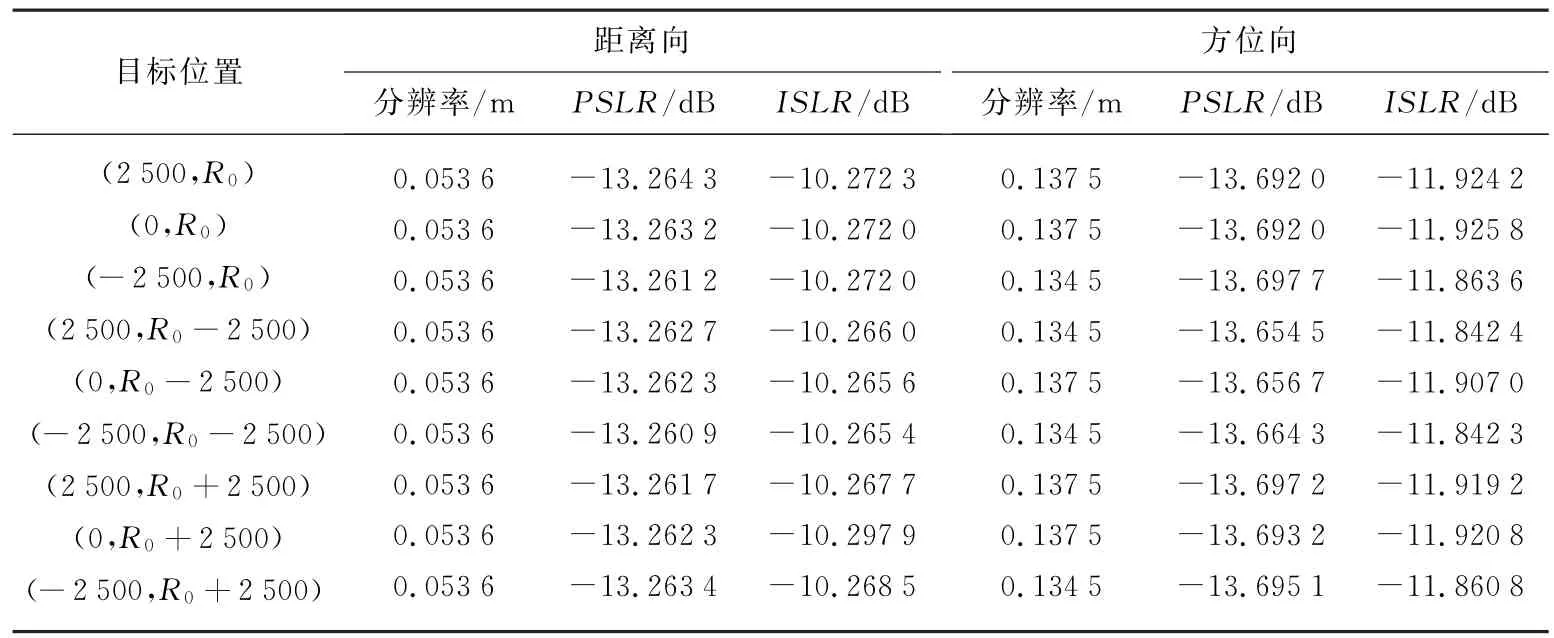
表2 本文算法成像结果质量评价
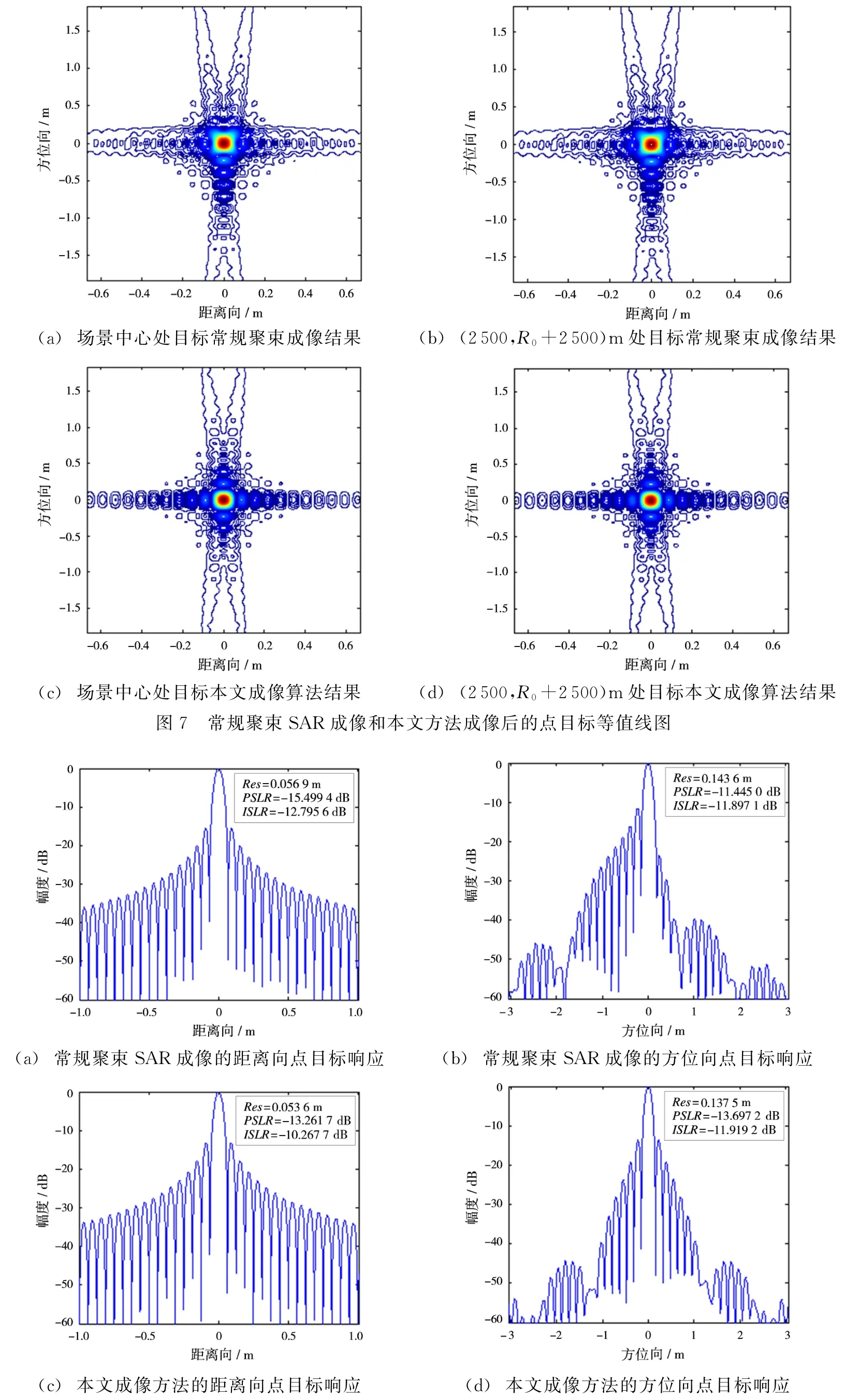
图8 常规聚束SAR成像和本文方法成像后的点目标方位向和距离向响应(以(2500,R0+2500)m处的点目标为例)
4 结束语
本文针对星载超高分辨率聚束SAR成像中“一步一停”假设不成立的情况进行分析。在星载SAR精确回波模型的基础上,分析各个畸变相位项对目标压缩的影响,忽略次要项,引入额外的距离徙动校正和方位频谱位移,从而将畸变后的信号补偿到未畸变的信号。最后,结合已有的聚束SAR“两步成像”方法,并利用Chirp-Z变换,提出了一种在“一步一停”假设不成立条件下的星载超高分辨率聚束SAR成像方法。通过仿真试验,该方法的有效性得到了验证。
本文的推导和仿真虽然是基于正侧视和小斜视角的,但2.1节中有关距离调频率和额外距离徙动校正的近似在大斜视角的情况下也是成立的。因此,可以推测该方法也适用于大斜视聚束SAR成像,但此时成像坐标系和目标的二维频谱都需要考虑斜视角的影响。
[1]盛磊,刘小平.高分辨率宽观测带星载SAR技术研究[J].雷达科学与技术,2013,11(2):130-135,140. SHENG Lei,LIU Xiao-ping.Research on High-Resolution Wide-Swath Spaceborne SAR Technology[J]. Radar Science and Technology,2013,11(2):130-135, 140.(in Chinese)
[2]MITTERMAYER J,WOLLSTADT S,PRATS P,et al.Staring Spotlight Imaging with TerraSAR-X[C]∥IEEE International Geoscience and Remote Sensing Symposium,Munich,Germany:IEEE,2012:1606-1609.
[3]ELDHUSET K.A New Fourth-Order Processing Algorithm for Spaceborne SAR[J].IEEE Trans on Aerospace and Electronic Systems,1998,34(3):824-835.
[4]包敏.地球同步轨道SAR与中高轨道SAR成像算法研究[D].西安:西安电子科技大学,2012.
[5]韩冰,张永军,胡东辉,等.星载滑动聚束SAR成像模型误差校正方法研究[J].电子与信息学报,2011,33 (7):1694-1699.
[6]CHEN J,ZENG D,LONG T.High Precision Radar Echo Modeling and Simulation Method[C]∥International Conference on Radar,Adelaide,Australia: IEEE,2008:469-473.
[7]PRATS P,SCHEIBER R,RODRIGUEZ M,et al. High Precision SAR Focusing of TerraSAR-X Experimental Staring Spotlight Data[C]∥IEEE International Geoscience and Remote Sensing Symposium,Munich, Germany:IEEE,2012:3576-3579.
[8]匡辉,陈杰,杨威.高分辨率星载SAR“停-走”模型误差精确补偿方法[C]∥第二届成像雷达对地观测高级学术研讨会,北京:国际数字地球学会中国国家委员会,2014.
[9]刘燕.高分辨率及新模式SAR成像算法研究[D].西安:西安电子科技大学,2012.
[10]LIU Y,XING M,SUN G,et al.Echo Model Analyses and Imaging Algorithm for High Resolution SAR on High-Speed Platform[J].IEEE Trans on Geoscience and Remote Sensing,2012,50(3):933-950.
[11]CURLANDER J C,MCDONOUGH R N.合成孔径雷达——系统与信号处理[M].韩传钊,等译.北京:电子工业出版社,2006:104-111.
[12]CUMMING I G,WONG F H.合成孔径雷达成像——算法和实现[M].洪文,胡东辉,等译.北京:电子工业出版社,2007.
[13]LANARI R,TESAURO M,SANSOSTI E,et al. Spotlight SAR Data Focusing Based on a Two-Step Processing Approach[J].IEEE Trans on Geoscience and Remote Sensing,2001,39(9):1993-2004.
[14]LIU F,DING Z,ZENG T,et al.Performance Analysis of Two-Step Algorithm in Sliding-Spotlight Space-Borne SAR[C]∥IEEE International Radar Conference,Washington,DC:IEEE,2010:965-968.

