基于滑模观测器的无速度传感器技术在PMSM中的应用

解佳鹏

(中船重工715 研究所，浙江杭州310010)

0 引言

永磁同步电机以其体积小、重量轻、功率密度大、功率因数高、效率高等优点，在高性能电力传动系统及工业自动化中占据了重要的地位，被广泛地应用于工农业生产、电动汽车、航天技术等领域。在高性能的传动系统中，需要对传动系统的速度及位置进行精确控制，常用的做法是使用位置速度传感器［1］，如光电编码器、旋转变压器等，不仅增加了硬件成本，而且降低传功系统的可靠性，为此无速度传感器技术得到迅速发展。

无速度传感器技术的电机转速辨识的方法经过多年的研究及发展，已经取得了很大的进展，并在工业自动化中得到了广泛的应用。目前运用较多的方法为模型参考自适方法，其算法复杂，且低速的辨识能力易受电机参数变化的影响，鲁棒性较差。近几年来，基于滑模观测器的速度辨识引起了人们的兴趣，滑模观测器不仅在宽的调速范围内有良好的动态性能，并且对电机的参数有较好的鲁棒性，具有良好的发展前景。

基于滑模观测器器的无速度传感器技术是将滑模变结构控制理论在电机速度辨识中的应用，本研究首先进行滑模观测器建模［2-4］，随后解决滑模变结构由于开关函数的频繁切换而引起的抖动问题［5-7］。经过仿真验证滑模观测器的正确性［8-9］，通过实验证明其在工程应用中可行性。

1 滑模观测器

PMSM 电机模型是一个耦合非线性的系统，通常采用坐标变化(CLACK 变换与PARK 变换)对其进行解耦分析。滑模观测器通过对定子模型建立观测器，间接观测出与速度相关的参数。

1.1 基于滑模观测器的PMSM 数学模型

本研究讨论的电机模型是基于隐性PMSM 电机的。根据PMSM 在静止坐标系α－β 的下的数学模型为:

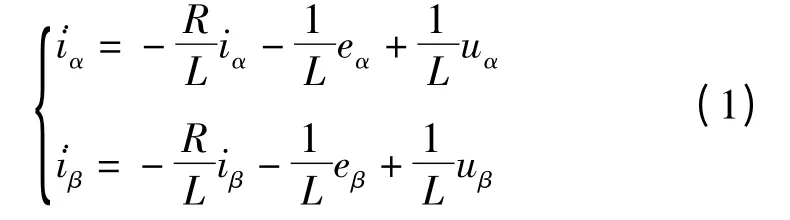
其中:

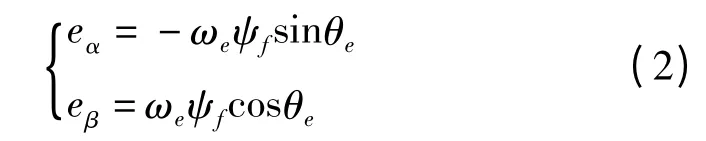
式(2)又被称为动生反电势。式中:R—定子电阻，L—相电感，ψf—永磁体磁链。

从式(2)可知，永磁同步电机的转子位置和转速与反电势有关，通过建立对反电势的观测器，间接提取转子的速度和位置信息。

根据传统的滑模观测器理论建立针对反电势的滑模观测器状态方程:

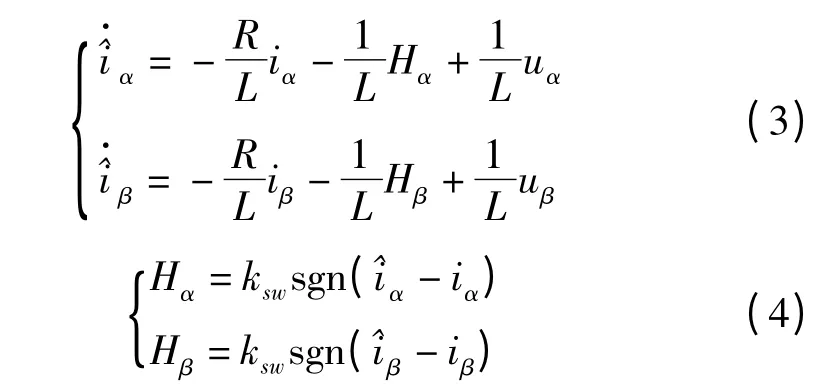
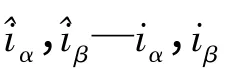
式中:的估计值;Hα，Hβ—切换信号;ksw—滑模系数。

在变结构控制系统中，滑动模态设计很关键，但目前在非线性系统的滑模面设计没有比较有效的方法，通常采用能产生稳定的的滑模动态的滑模面，本研究定义滑模面为:

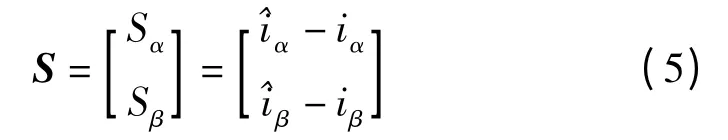
1.2 稳定性的证明及滑模系数ksw的选择

变结构控制系统的稳定性是指，在正常运动阶段保证系统状态趋近并进入滑动模态，且滑动模态运动阶段保证滑动运动稳定。稳定性的关键问题在于设计出适当的变结构规律，使得系统状态在有限时间内进入滑动模态，这可通过李雅普诺夫稳定性理论来分析解决。

因此，构造李雅普诺夫函数:

将式(1，2)代入式(7)，得:

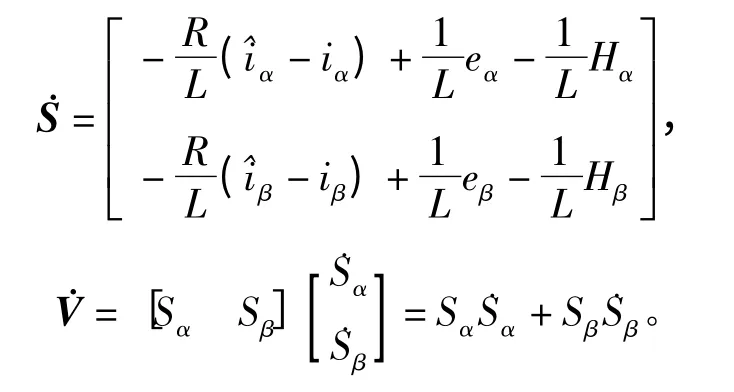
因此在设计参数时，只需满足下式:

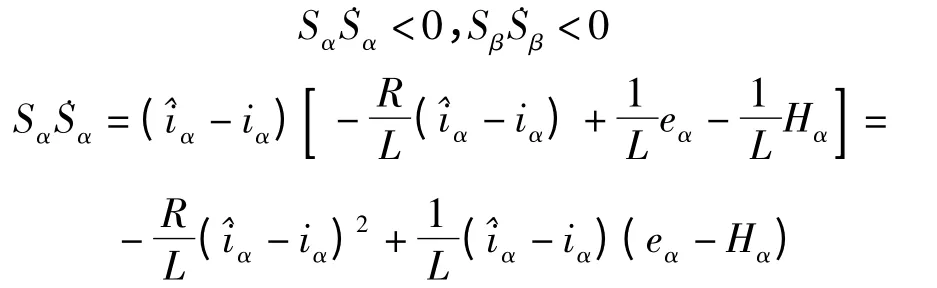
使Hα＞eα，同理Hβ＞eβ，

即ksw＞max(|eα|，|eβ|)，则可保证观测器收敛，一般采用ksw=1.5ψf|ωe|。

当系统在滑模面上运动时，系统满足S=˙S=0，因此:

1.3 防抖措施

由于开关函数的频繁切换而引起的抖动会引起比较大的转矩脉动，在低速下运行时，会使系统不稳定，这是滑模变结构控制的固有缺陷。在实际应用中，常使用饱和函数代替开关函数，以减小抖振。饱和函数的表达式如下:

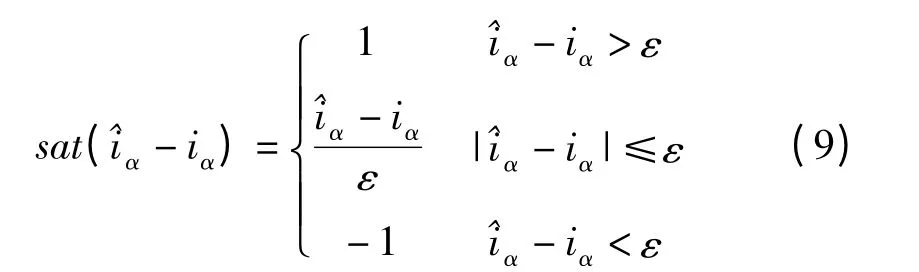
通过调节ε 的值，有效地减小滑模变结构系统的运动点在运动时的抖振，饱和函数如图1所示。

2 转子位置和速度的计算

由电机的数学模型式(2)可以知道，从反电势中可以提取出转子的速度和位置:

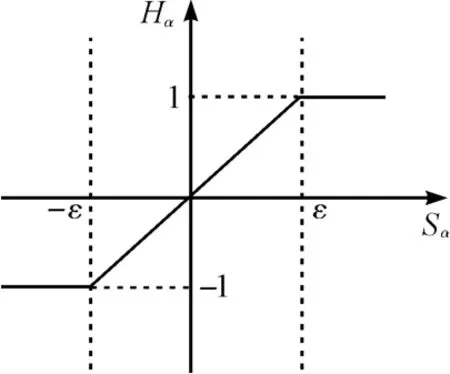
图1 饱和函数图

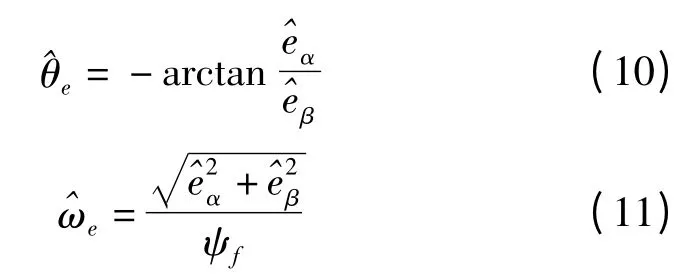
由于采用了滑模控制，计算所得到的H 信号中有大量的开关信号，信号需要低通滤波后才能得到连续的反电势。

滑模观测器的结构框图如图2所示。

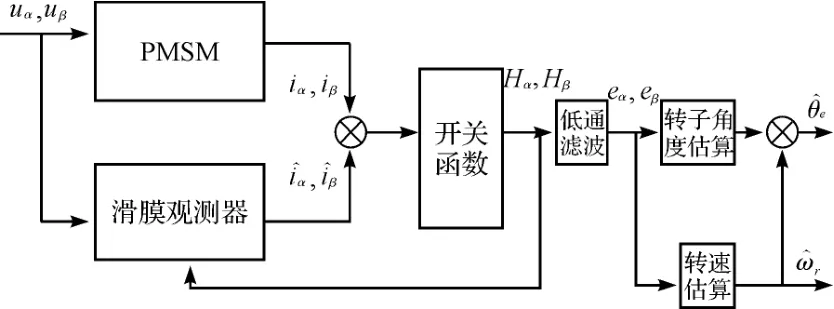
图2 滑模观测器结构图

由于引入低通滤波器，即引入了惯性环节，会导致相位延迟，为了提高算法的实时性，需要进行角度补偿。

3 仿真分析

本研究在Matlab2009a/Simulink 平台下建立仿真模型。滑模观测器的仿真框图如图3所示。

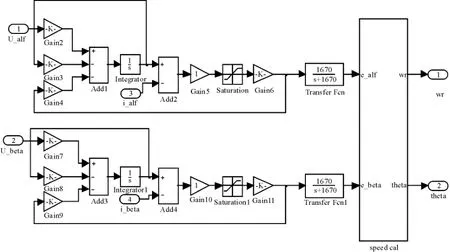
图3 为滑模观测器的仿真框图

仿真参数:额定功率为1.6 kW，电机的定子电阻Rs=0.958 5 Ω，电感为5.25 mL，极对数为4，转矩常数为1.096 N·m/A，转动惯量为0.000 63 N·m2。滑模参数为:ksw=100，ε=1，低通滤波器的截止频率为1 670。

仿真结果如下:

电机实际转速与SMO 估计转速如图4所示，可以看出SMO 可以辨识出电机的转速，对于电机转速具有很宽的辨识范围。

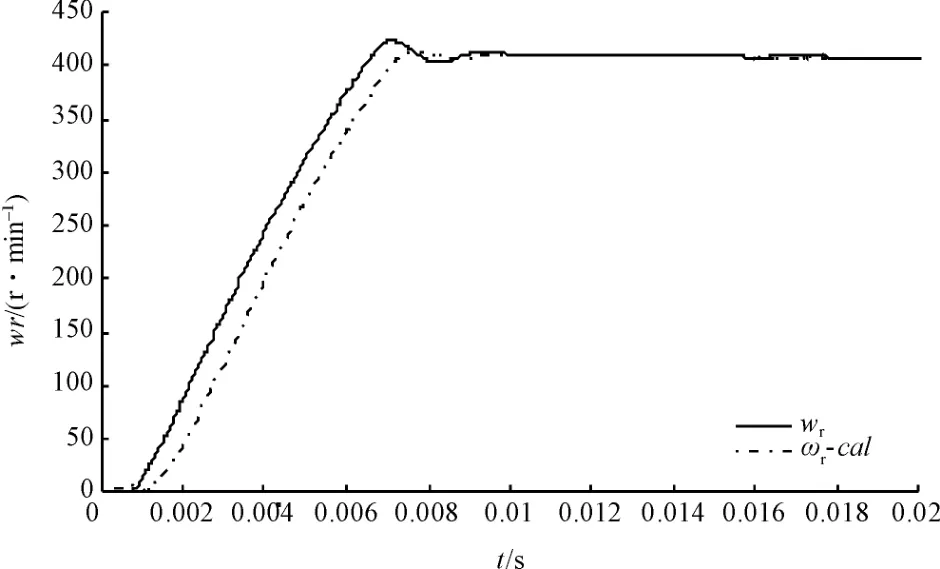
图4 转子的实际转速与SMO 估计转速

SMO 辨识出的转子磁链位置与电机转子磁链实际位置的比较如图5所示。在SMO 模型中由于引入低通滤波器，即引入了惯性环节，这样导致了估计出的转子位置对于实际转子位置有一个相位延迟，因此在实际应用中时要对SMO 估算出的转子位置进行角度补偿。

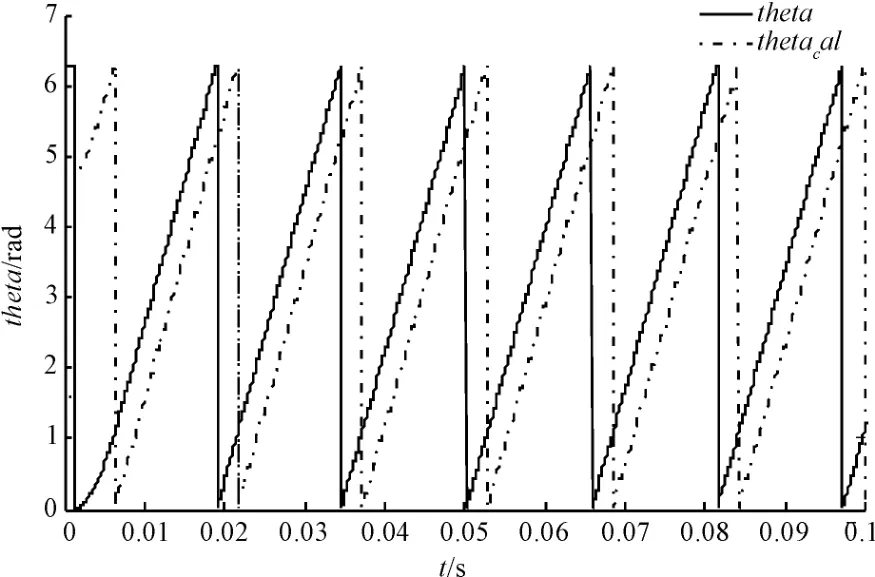
图5 转子磁链的估计位置与实际位置

4 实验分析

实验内容主要通过将SMO 算法数字化，在DSP中进行编程，验证SMO 算法，并替带速度传感器进行双闭环矢量控制。硬件原理框图如图6所示。

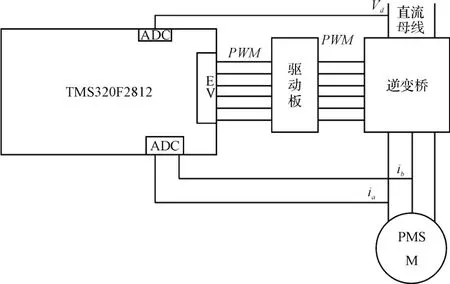
图6 系统原理框图

从图6 可以看出需要对电机的两相电流和直流母线电压进行采样，对6 路输出信号进过驱动板放大隔离控制逆变桥。

电机的参数:Rs=0.9，Ls=4.35 mH，极对数P=8。

速度辨识图如图7所示。纵坐标为转速的标幺值(单位1 为750 r/min)，通过DSP 中的SMO 算法可以估算出电机稳态时的速度。

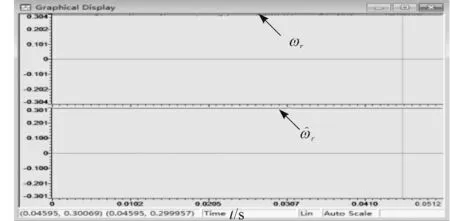
图7 速度估算图

转子磁链位置估算图如图8所示，纵坐标为角度的标幺化值(单位1 为360°)，从图8 中可以看出实际应用与仿真结果类似，SMO 估算出的转子磁链位置滞后于实际转子磁链位置，需要进行角度补偿。加入角度补偿后的转子磁链估算图如图9所示。

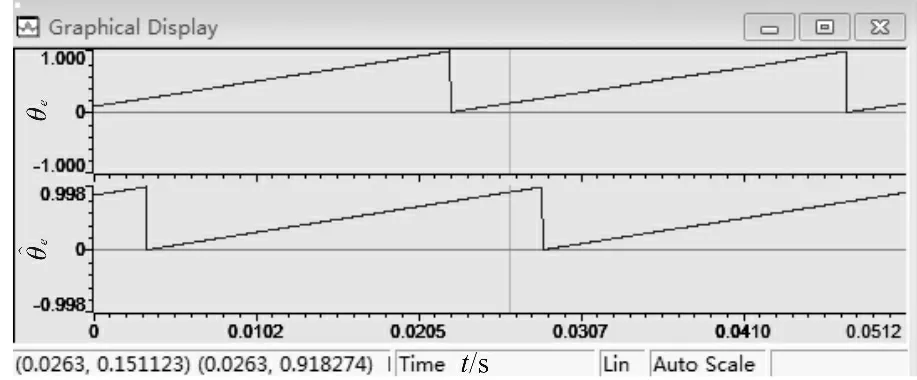
图8 转子磁链位置估算图

当电机在启动过程中，反电势很小，很难通过SMO 估算出电机的转速及位置，因此在电机的启动过程中，往往采用爬坡软启动的方式，让电机转速缓慢启动，使电机在低速状态下运行在开环状态下，当电机转速达到SMO 可以估算出来的下限时在切换到闭环模式运行。

5 结束语

本研究对基于SMO 的无速度传感器技术进行了建模仿真和实验研究。研究结果表明，滑模观测器可以估算出PMSM 电机的速度和转子磁链位置，基于滑模观测器的无速度传感器技术可以替代传统的传感器技术应用于电机的控制中，构建双闭环矢量控制系统。基于滑模观测器的无速度传感器技术不仅解决了传统传感器技术带来的种种工程瓶颈，而且进一步降低了传动系统的成本，具有很大的工程应用前景。

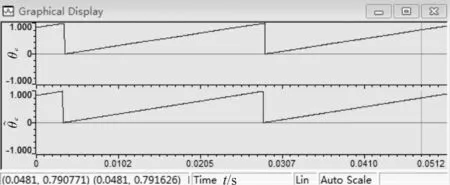
图9 加入角度补偿后的转子磁链位置估算图

［1］阮 毅，陈维钧.运动控制系统［M］.北京:清华大学出版社，2006.

［2］张 群，李 宏，郑 勇.一种新型滑模观测器的永磁同步电机无传感器控制［J］.微特电机，2010.

［3］JIANG Dong，ZHAO Zheng-ming，WANG Fei.A Sliding Mode Observer for PMSM Speed and Rotor Position Considering Saliency［C］.Power Electronics Specialists Conference，2008.PESC 2008.Rhodes:［s.n.］，2008:809-814.

［4］ZHANG Yan，Vadim Utkin.Sliding Mode Observers for:Electric Machines-An Overview［C］.Industrial Electronics Society，IEEE 2002 28th Annual Conference.Seville:［s.n.］，2002:1842-1847.

［5］KIM H，SON J，LEE J.A high-speed sliding-mode observer for the sensorless speed control of a PMSM［J］.IEEE Transactions on Industrial Electronics，2011，58 (9):4069-4077.

［6］高仁璟，李希伟.PMSM 无传感器控制的新型滑模观测器设计［J］.电机与控制应用，2014(11):12-18.

［7］苏义鑫，何国星，张 婷.基于滑模观测器的PMSM 控制系统研究［J］.工业控制计算机，2010(5):63-64.

［8］毛文杰，范坚坚，吴建华，等.交流伺服PMSM 系统模糊PI 矢量控制设计［J］.轻工机械，2013，31(3):43-46.

［9］金树强，南余荣.基于改进滑模观测器的PMSM 无位置传感器矢量控制系统［J］.微特电机，2013(3):46-49.