无人机雷达天线稳定平台的优化设计研究

陈国虎，俞竹青，吕学能

(1.杭州航海仪器有限公司，浙江杭州310024;2.常州大学机械工程学院，江苏常州213164)

0 引言

稳定跟踪平台是惯性技术应用的重要领域之一，其功能是隔离载体的角运动和线振动使被稳定对象相对某方位保持稳定并可对目标进行自动跟踪［1-2］，由光纤陀螺仪测定平台实时姿态，通过嵌入式工控系统分析运算、光电编码器与交流伺服电机组合驱动平台以实现天线指向的稳定。本研究的稳定平台应用于无人机机载雷达，隔离由于震动导致的雷达探测误差，由于机型较小，载重有限，传统雷达稳定平台重量、转动惯量较大，反应不够灵活。

针对上述问题，本研究对稳定平台进行基于刚度、强度条件下以减轻重量为目标的优化设计，对提高平台灵敏度、降低功耗、扩大稳定平台的应用领域有重要意义。

1 稳定平台结构模型

稳定平台通常有多种结构布局和支承方式。一般采用机电式两轴［3］或三轴多框架结构［4-5］(稳定平台结构布局如图1所示)。三轴方式较两轴方式增加了在方位方向对天线高频振动的过滤，其工作性能较好，为了达到较好性能，项目采用三轴结构。

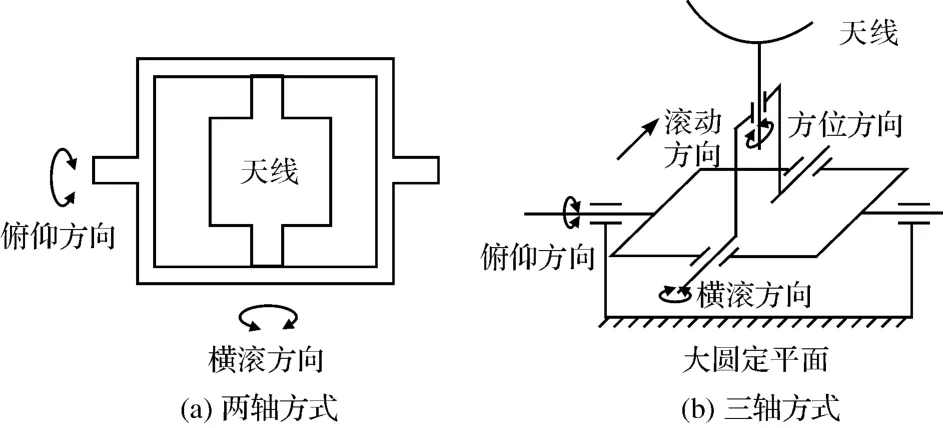
图1 稳定平台结构布局

根据上述原理，以满足稳定平台设计技术要求为前提，考虑电机、减速机、陀螺仪等结构件的布置，利用Creo2.0 完成模型设计，本研究初步确定了稳定平台的机械模型。

稳定平台三维模型如图2所示。

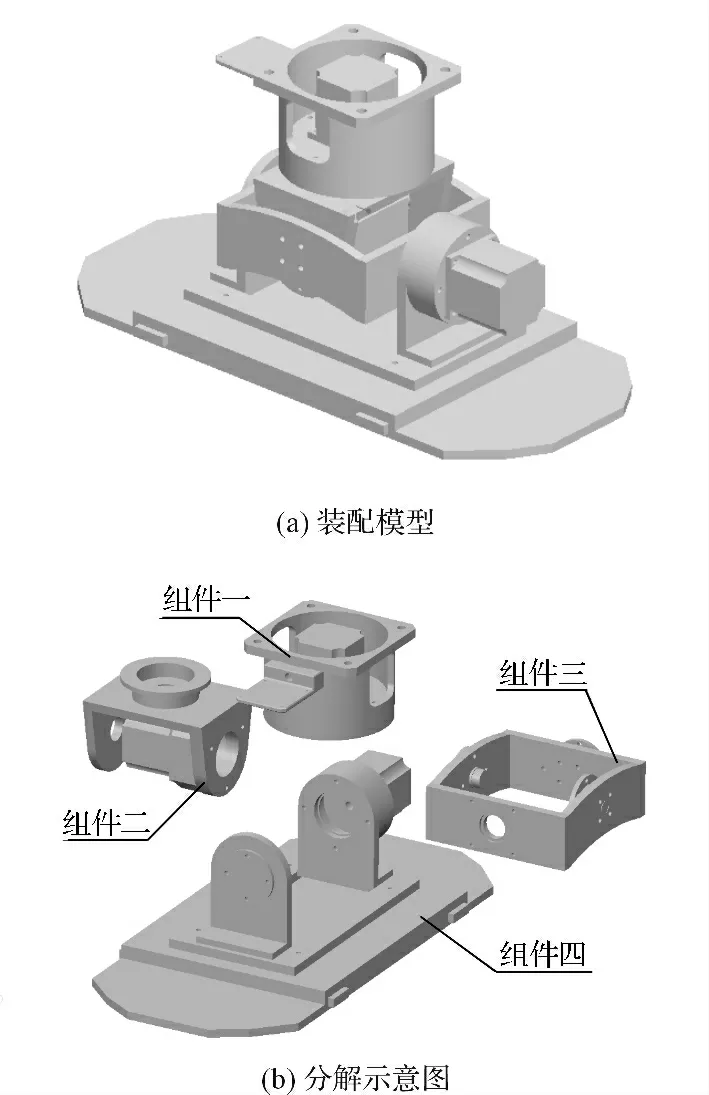
图2 稳定平台三维模型

2 稳定平台载荷分析

在工作时，随着飞行姿势的改变，在转弯、俯冲、加速时稳定平台姿态自动调整以确保雷达天线的指向稳定。显然，稳定平台最大载荷出现在飞机同时加速、转弯、俯冲时，稳定平台各组件的载荷为加速度以及姿态角的函数:F=f(a1x，a1y，a1z，α，β，r)。本研究对稳定平台进行优化设计，应分析各组件在最严酷工作状态的姿态角所对应的载荷，将其作为有限元分析的边界条件，以重量为优化目标，确保稳定平台的刚度性能指标要求，展开优化设计。

本研究为分析各组件的载荷情况应分别建立坐标系(坐标系如图3(a)所示):坐标系Ⅰ(cs1):组件一与飞机的装配面中心点为原点，飞机飞行方向为x 轴正向，飞机升力方向为z 轴;坐标系Ⅱ(cs2):以组件二的z 传动轴零件上表面中心为原点，以平行于飞行方向为x 轴，飞机升力方向为z 坐标，坐标系随组件二的转动而转动;坐标系Ⅲ(cs3):以组件二与组件三的装配轴为y 轴，在y 轴上确定坐标原点，使得在平台的姿态角都为零时，坐标系Ⅲ上的z 轴，与坐标系Ⅱ上z 坐标重合，随组件三的转动而转动;坐标系Ⅳ:以组件四与组件三的安装轴为x 轴，以在组件四的对称平面向上为z 轴。

定义姿态角:

α—方位角:以飞机的升力方向轴为法线;

β—俯仰角:以飞机的左侧轴为法线定义;

γ—横滚角:以飞机的飞行方向定义法线。

上述角均以右手定则定义方向。各组件之间的坐标关系是由3 个姿态角决定的［6］(坐标变换示意图如图3(b)所示)。

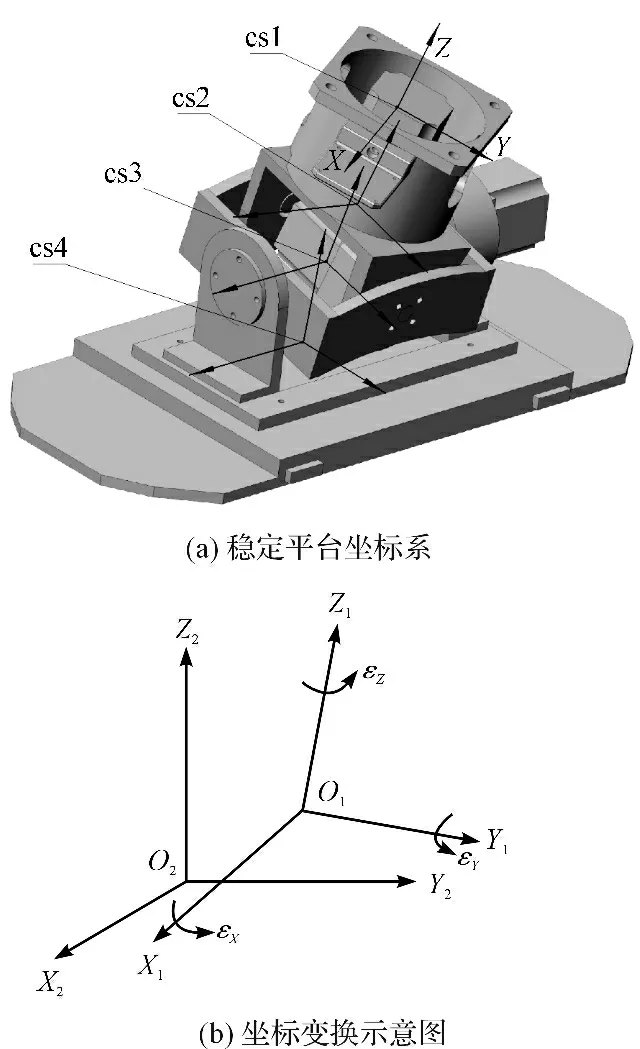
图3 建立坐标系

第一个坐标系到第二个坐标系的变换是沿z 轴旋转－α 角，第二个坐标系到第三个坐标系的变换是沿y轴旋转β，第三坐标系到第四坐标系的变换是沿x 轴旋转γ。坐标系之间的转换满足式(1)的关系:

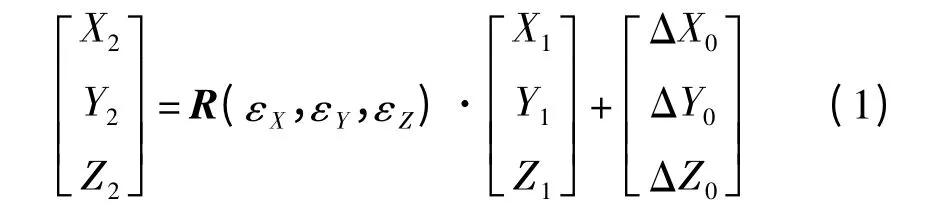
式中:R(εX，εY，εZ)—关于欧勒角为自变量的变换矩阵，反应到前述建立的坐标系中进行变换时，由实际姿态角迭代取值。

其中:

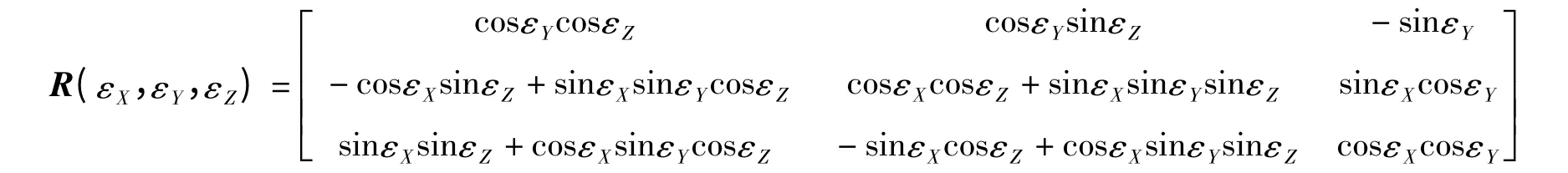
根据姿态角的定义:ε1－＞2=(0，0，－α)，ε1－＞3=(0，β，－α)，ε1－＞4=(γ，β，－α)，ε2－＞3=(γ，β，－α)，ε2－＞4=(γ，β，0)，ε3－＞4=(γ，0，0)，ε4－＞3=(－γ，0，0)。式(1)中(ΔX0，ΔY0，ΔZ0)由相对于变换的坐标原点决定。对于所建坐标系以Iijo表示坐标系j 的原点在坐标系i 中的坐标，根据模型的几何模型有式(2)的关系:

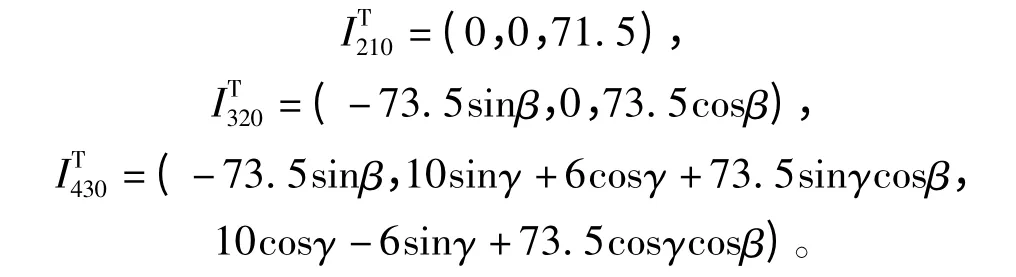
在稳定平台工作过程中，飞机通过组件一将飞行状态、飞行姿态传递给稳定平台。因此组件一的姿态、加速度与飞机相同，在稳定平台在各组件中保持相同，在不同坐标系中，加速度的表示形式有所区别，规定:aij表示在第i 坐标系中组件j 的加速度，则a44= R(ε1－＞4)·a11关系，重力加速度g 在各坐标系i 中的关系有:g4=(0，0，g)，g4=R(ε3－＞4)g3=R(ε2－＞4)g2=R(ε1－＞4)g1，得:

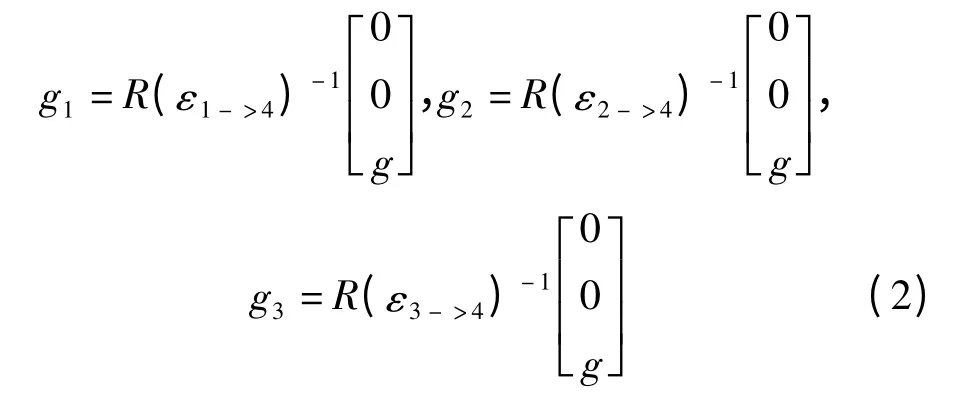
在稳定平台工作时，组件四、三、二、一依次组装，载荷依次累积，因此为分析各组件的受力，从组件四开始。本研究在坐标系Ⅳ中将重力加速度与飞机加速度表示为等效重力加速度g4'，有等效重力加速度［7］可表示为:

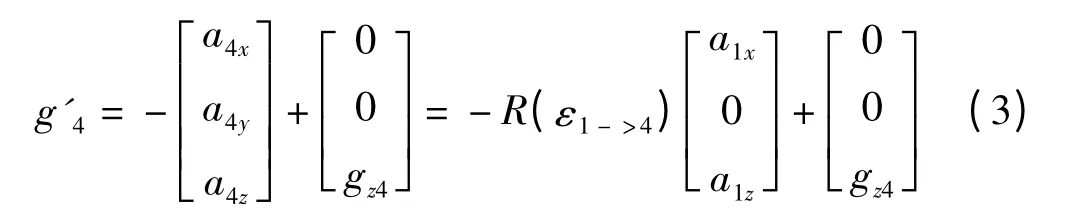
其中:组件一与机体相固定连接，其加速度与飞机相同。将重心位置表示为下式所示:

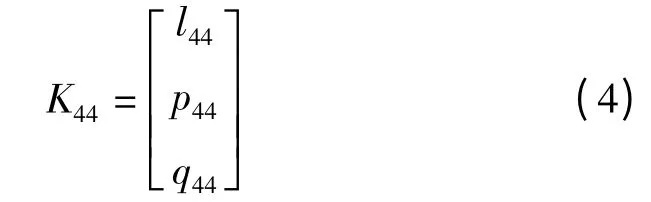
式中:l44，p44，q44—在坐标系四中重心的坐标。

组件四的受力如图4所示，重心坐标为(l，p，q)根据力学平衡原理:∑F = 0，∑M = 0，得:

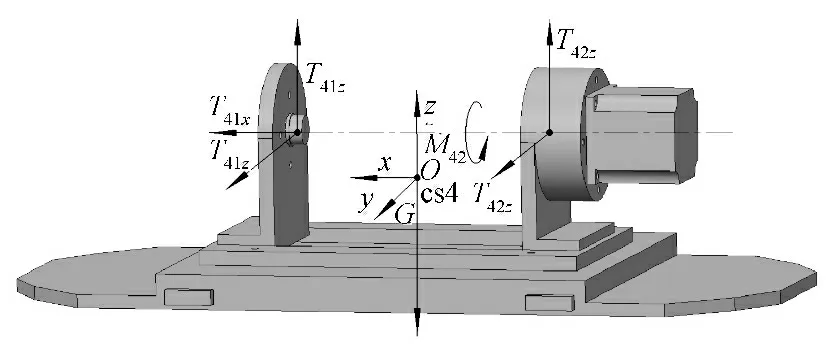
图4 组件四受力示意图

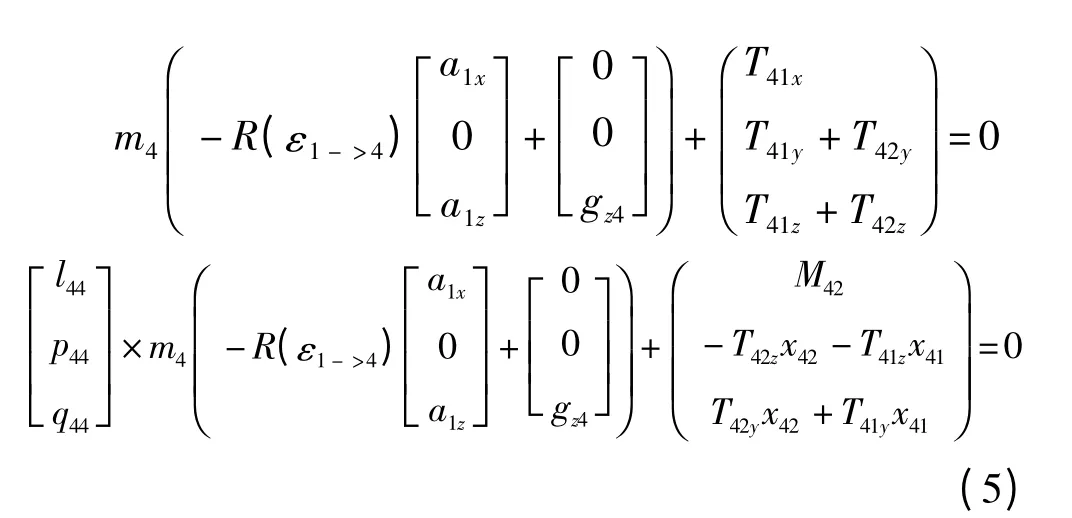
根据式(5)计算得:

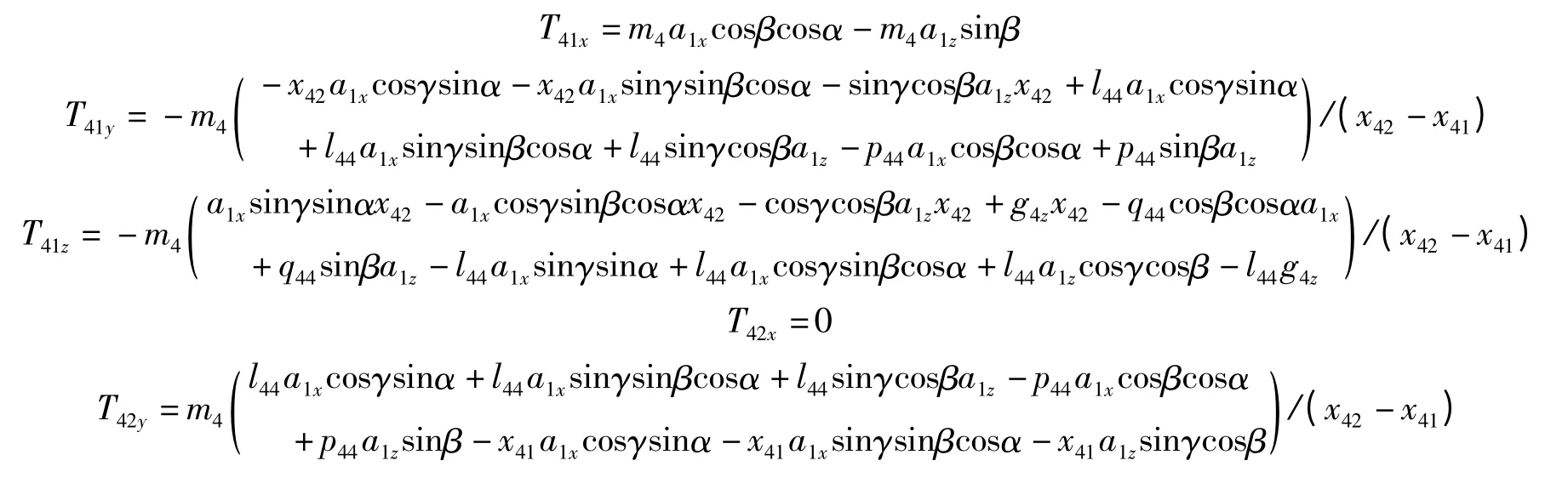
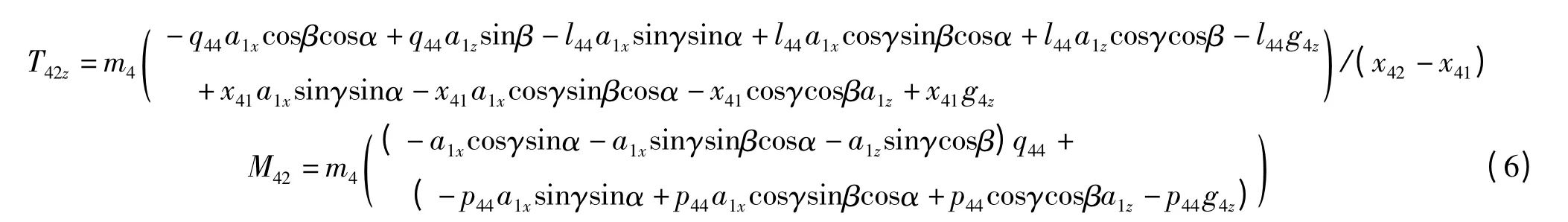
以此类推，得组件三、组件二、组件一受力载荷情况与飞行姿态角以及飞行加速度的关系:

3 稳定平台各组件优化设计

本研究通过对稳定平台的载荷分析，取得各组件的载荷与飞机飞行姿态的表达式关系，上述表达式中，各组件重量、重心位置均可在三维模型中测定，而飞行加速度向量为无人机的工作参数，进行优化设计时选取a11=(a1x，0，a1z)=(2g，0，2g)，即单向最大加速度为2 倍重力加速度。

因此所有载荷均为关于姿态角(α，β，γ)的函数［8］。对于组件四(天线与天线支架)来说受到的载荷是T41、T42以及组件四受到的等效重力，有限元分析时:T41，T42是位移约束点。因此，本研究分析组件四时，为求最大值，取等效重力为优化函数，同时考虑到姿态角的取值范围，组件四的优化函数表示为:

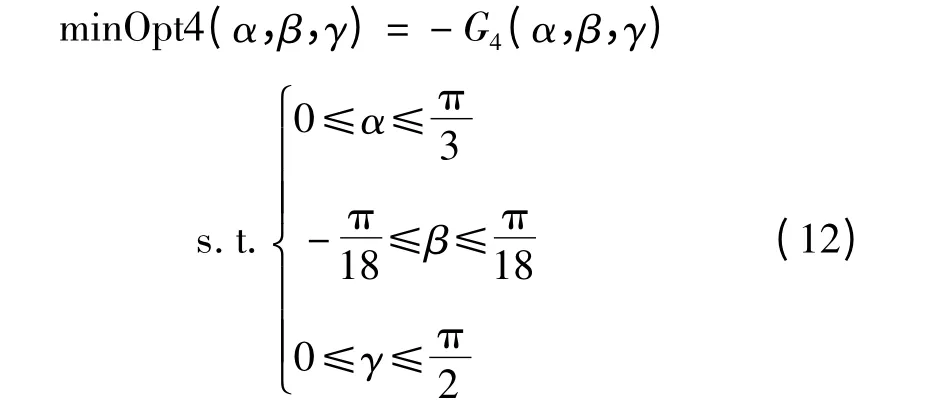
式中:G'4—组件四受到的等效重力。

以此类推，组件三、组件二、组件一的优化函数分别表示为:

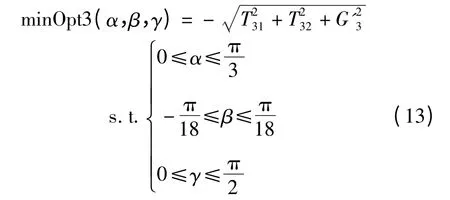
式中:G'3—组件三受到的等效重力。

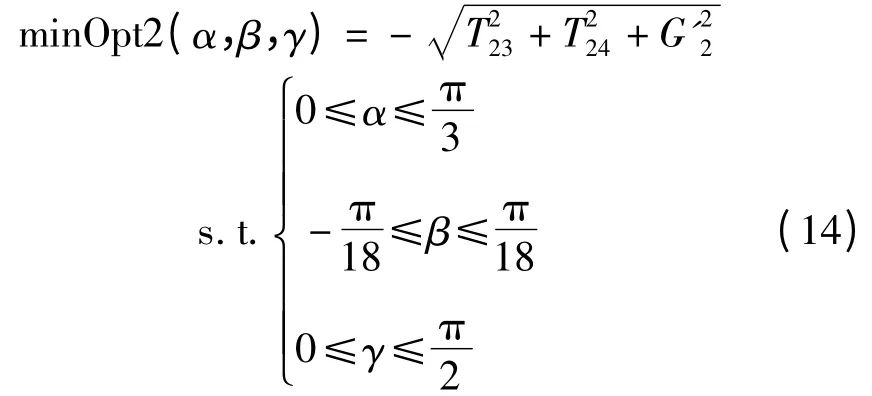
式中:G'2—组件二受到的等效重力。

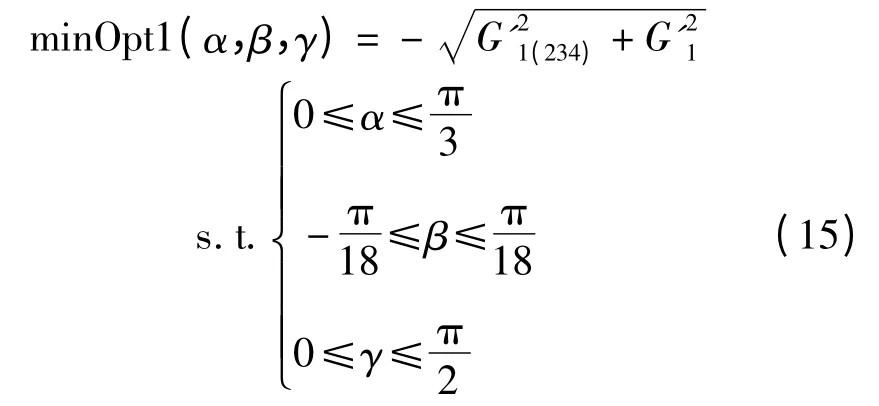
式中:G'1(234)—第一坐标系中，组件二受到的等效重力。

本研究运用Matlab 的fmincon()优化工具，求解上述表达式，得:

当α=0°，β =10°，γ =5°时组件一取得最大等效载荷299.01 N。

当α=0°，β=10°，γ=0°，时组件二取得最大等效载荷62.83 N。

当α=－37°，β=10°，γ =0°时组件三取得最大等效载荷162.83 N。

当α=0°，β=10°，γ=20°时组件四取得最大等效载荷－36.185 5 m/s2。

本研究将上述姿态角代入受力表达式，求解处各组件的在严酷载荷位置时，具体载荷值作为creo2.0中simulate 分析的边界条件［9-12］，运行静态分析后以组件厚度为优化变量，组件重量为优化目标，最大位移不超过0.01 mm 为限制条件，同时根据结构需要设定厚度不小于2 mm 执行优化设计研究，组件一优化前后效果如图5所示。同理类推执行其他各组件。汇总优化研究结果如表1所示。

图5 组件一有限元分析情况

表1 稳定平台优化前后重量与最大位移对比汇总

稳定平台总体重量由4.425 kg 优化至2.96 kg，稳定平台重量缩减了约1/3，减重效果显著，同时位移指标满足要求。该设计的重点是对于稳定平台支撑结构进行了优化，对伺服电机传动部件保持不变，在驱动力保持不变的情况下，稳定平台转动惯量下降，提升了平台的探测灵敏度，平台控制探测精度由0.08°提高至0.05°。

4 结束语

本研究在完成稳定平台的优化设计后，根据优化后的参数修正模型，并进行样机试验，现稳定平台已在某无人机上成功应用，工作状态良好。对雷达天线稳定平台的优化设计，使得稳定平台的重量得到有效地降低，同时提升了稳定平台的工作灵敏度，不仅减小了的对无人机的承载能力，同时对于扩展稳定平台的应用领域具有实际意义。笔者在研究过程中探讨了采用坐标变换方式和力学原理求解相对运动组件载荷与不同输入姿态、加速度的关系，并应用Matlab、Creo/Simulate等软件，对数学模型、机械模型进行优化求解的方法，对于解决具有旋回、俯仰运动的发射装置、挖掘机等类似设备的载荷问题具有借鉴意义。在本研究时着重对于组成组件的厚度尺寸进行了优化，优化目标较为单一，在未来研究时应考虑在减轻重量的同时研究在适当位置增加筋板的方式达到既减轻重量的目的，同时增加机体刚度，减少变形量。

［1］ZHOU Xiang-yang，YU Rui-xia，LI Jian-ping，et al.Structure optimal design of roll gimbal for an aerial three-axis ISP based on FEM modal analysis［C］//IEEE Proceedings of ICMTMA.Shanghai，China:［s.n.］，2011:373-376.

［2］HIKERT J M.Inertially stabilized platform technology concepts and principles［J］.IEEE Control Systems Magazine，2008(12):26-46.

［3］毕永利，刘 洵，葛文奇，等.机载多框架陀螺稳定平台速度稳定环设计［J］.光电工程技术，2004，31(2):16-18.

［4］张 强，吴云东，张 超.低空遥感小型三轴陀螺稳定平台的设计与实现［J］.测绘科学技术学报，2012，22(4):276-280.

［5］苑大威，黄 波，刘伊华.基于DSP 的地磁陀螺组合测姿系统［J］.兵工自动化，2014(2):92-95.

［6］袁春桥，范新成，王志水，等.坐标系统通用转换模型的研究［J］.山东科技大学学报:自然科学版，2007，26(6):11-13.

［7］刘 晓，赵铁石，高佳伟.非贯性系下舰载稳定平台动力学建模及特征分析［J］.机器人，2014，36(4):411-418.

［8］王 晨，董景新，高宗耀，等.火箭弹大动态单轴平台贯导系统姿态算法［J］.中国惯性技术学报，2012，20(3):257-261.

［9］张继春，徐 斌，林 波.Pro/engineer Wildfire 结构分析［M］.北京:机械工业出版社，2005.

［10］晏袓根，王瑞泽，孙智慧，等.四自由度并联机器人运动学分析［J］.包装与食品机械，2014(2):37-41.

［11］余杰先，吴 朋，曾 奇.一种新的并联机器人精度标定算法［J］.机电工程技术，2014(4):24-27.

［11］胡 峰，骆德渊，段栋栋，等.基于Pro/E 与Simulik 的Delta 并联机器人运动仿真［J］.机电工程，2012，29(8):982-984.