一种新型全控式自平衡爬楼车的设计与研究

刘柄辰，宋其江，凌志成，季 鹏

（东北林业大学 机电工程学院，黑龙江 哈尔滨 150040）

0 引言

爬楼车是一种具有一定实用意义的家用载物车，可适应楼梯和平地两种地形。目前，各国关于爬楼车的研究已有数百年的历史。在众多设计方案中，较为有代表意义的主要有以下几种： 履带式、行星轮式、步进式、仿人式等[1～4]。其中，尤以行星轮式爬楼车结构简便，易于控制，是目前众多方案中较为理想的。然而，在目前对行星轮全控式爬楼车的研究中，并未提出切实有效的对缓解冲击力的方法。同时，现方案中对爬楼车重心调节方式多靠机械调节，可靠性有待加强[5～7]。因此，本文设计了一种增加了缓冲轮的全控式爬楼车，并给出了一种通过程序控制实现自动化重心调节的方案。经理论分析和等效模型试验验证，该方案较为可靠。

1 行星式爬楼车越障原理分析

目前，行星式爬楼车主要有“半控式”和“全控式”两种。“半控式”爬楼车的爬楼能力主要取决于地面所能提供的摩擦力；而“全控式”爬楼车的爬楼能力则取决于爬楼车自身的几何参数。以下给出两种爬楼车爬楼原理的分析。

1.1 “半控式” 行星轮爬楼车越障原理分析

由于爬楼车在爬楼过程中速度较低，因此可以用静力学知识对爬楼过程中的受力情况进行分析[8]。建立如下行星轮越障力学模型：F1、F2为电机提供给行星轮1、2的驱动力；N1、N2为地面提供给行星轮1、2 的支持力；Ff2为行星轮2 受到地面的摩擦阻力；整车重心距行星轮距离为L；整车质量为G；行星轮轮直径为D；楼梯高度为h;行星轮1 与楼梯所成角度为α。

图1 爬楼车越障原理简图Fig.1 Obstacle-surmounting principle sketch of stairs-climbing vehicle

根据水平、竖直方向受力平衡关系及力矩平衡关系列得如下平衡方程：

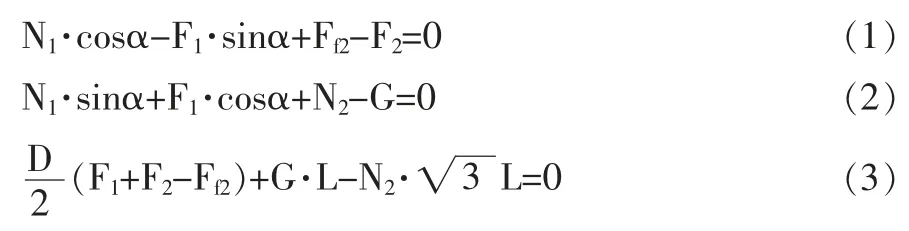
由于行星轮1、2 的驱动力矩由同一个电机提供，假设驱动力矩平均分配，且忽略摩擦力（Ffi=f·Ni），则有：

式中： φ—地面附着系数。

可解得：

由上述分析可知 “半控式” 行星轮爬楼车的最大越障高度主要取决于地面附着系数和行星轮直径。这种结构具有较大的可靠性，当行星轮与障碍接触时方可进行爬楼动作。

1.2 “全控式” 爬楼车越障原理分析

“全控式” 爬楼车的主要依靠自身结构完成爬楼动作。由前面推导的数学关系易知，爬楼车最大越障高度即为两行星轮轮心距离：

“全控式” 爬楼车的由于完全依靠电机驱动行星架完成翻转运动具有操控简单的优点。但同时，爬楼瞬间产生了较大的冲击力，噪音较大，且对车体强度有较高要求。

2 全控式自平衡爬楼车的设计

2.1 爬楼车结构尺寸的设计

本设计采用 “全控式” 爬楼车的结构方式，增加了缓冲轮。我国 《建筑楼梯模数协调标准》 规定： 普通楼梯（a-踏步高，b-踏步宽）的高度a 不能大于210mm，同时不能低于140mm；楼梯宽度b 不能超过320mm,，同时不能低于220mm；而且，楼梯的宽度和高度应该满足关系： 2a+b 小于等于600mm[9]。本设计爬楼车要能适应标准规定的楼梯尺寸范围。

假定楼梯高度为140mm,楼梯宽度为220mm。设爬楼车缓冲轮半径为R，支撑轮半径为r，行星架臂长为t。通过对楼梯尺寸和爬楼车实际工作情况的分析，如图2 所示，列出如下方程：

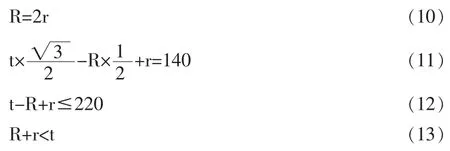
解上述方程并将结果圆整得到爬楼车主要尺寸： 缓冲轮半径为100mm，支撑轮半径为50mm, 行星架臂长160mm。

2.2 爬楼车的受力分析

按照图2 爬楼车工作简图，对爬楼车工作过程中的实际受力情况利用静力学知识进行分析。

F1为电机给缓冲轮的驱动力，F2、F3为电机提供给行星轮的驱动力；N1为台阶给缓冲轮的支持力，N2、N3为地面提供给行星轮的支持力；Ff2、Ff3为行星轮2 受到地面的摩擦阻力；G 为爬楼车的重力，假定L 为爬楼车重心距行星架中心的距离。列得改进后的爬楼车受力平衡方程如下：

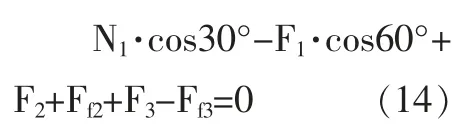
假设忽略摩擦力Ff2=Ff3=0，由力矩关系可得：

令F2=F3=F，则F1=1.6F，解得： N1=1.38F

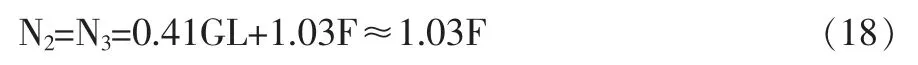
通过受力分析可知，缓冲轮的引入分担了大部分支撑轮工作中的冲击力。因此，这种改善是有效的。

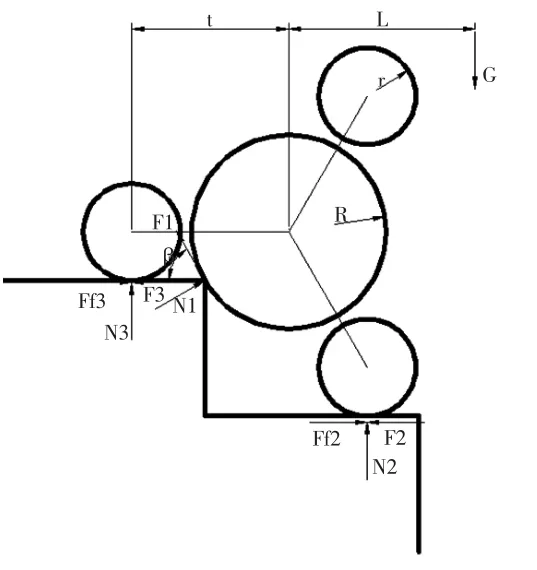
图2 爬楼车工作状况简图Fig.2 Sketch in working conditions of stairsclimbing vehicle

2.3 爬楼车重心平衡的设计

爬楼车的平衡保持是实现爬楼自动化的一个关键点。现有的爬楼车中心调节主要依靠机械结构实现。爬楼车重心是否平稳，将影响其在上楼过程中的稳定性，而其车体本身的不稳定也将造成运送货物过程中的震动，影响运输质量同时，对爬楼车的结构寿命也有重要影响。故本设计的另一大部分主要是针对爬楼车平衡自动化的设计，一方面要实现爬楼车在上楼过程中本身受力的平衡，另一方面，结合相关自动化技术，利用相关软件控制，也加大了车体本身平衡的可靠性。现通过对单摆平衡原理的分析，给出一种通过程序控制实现平衡的方案。整车简化模型如图3 所示。

要达到使物体保持平衡这一目的，可以通过增加额外的受力的方法，使得恢复力与位移方向相反。控制爬楼车底部车轮，使得它作加速运动。这样站在小车上（非惯性系，以车轮作为坐标原点） 分析倒立摆受力，它就会受到额外的惯性力，该力与车轮的加速度方向相反，大小成正比。这样倒立摆所受到的回复力为：

图3 爬楼车自平衡受力模型Fig.3 Self-balancing mechanical analysis model of stairs-climbing vehicle

式中，由于θ 很小，所以进行了线性化。假设负反馈控制是车轮加速度a 与偏角θ 成正比，比例为k1。如果比例k1＞g（g 是重力加速度），那么回复力的方向便于位移方向相反了。

此外，为了使得倒立摆能够尽快地在垂直位置稳定下来，还需要增加阻尼力。虽然存在着空气和摩擦力等阻尼力，相对阻尼力比较小。因此需要另外增加控制阻尼力。增加的阻尼力与偏角的速度成正比，方向相反。因此式（19）可变为：

按照上面的控制方法，可把倒立摆模型变为单摆模型，能够稳定在垂直位置。因此，可得控制车轮加速度的控制算法：

式中： θ—车模倾角；θ'—角速度；k1、k2均为比例系数；两项相加后作为车轮加速度的控制量。只要保证在k1＞g、k2＞0 的 条件下，可以使得车模像单摆一样维持在直立状态。其中有两个控制参数k1、k2，k1决定了车模是否能够稳定到垂直平衡位置，它必须大于重力加速度；k2决定了车模回到垂直位置的阻尼系数，选取合适的阻尼系数可以保证车模尽快稳定在垂直位置。这两个系数的作用如图4 所示。整车的运动学模型如图5 所示，模型可按如下方法建立：

假设倒立车模简化成高度为L，质量为m 的简单倒立摆，它放置在可以左右移动的车轮上。假设外力干扰引起车模产生角加速度x（t）。沿着垂直于车模地盘方向进行受力分析，可以得到车模倾角与车轮运动加速度以及外力干扰加速度a（t）、x（t）之间的运动方程。

车模运动方程：

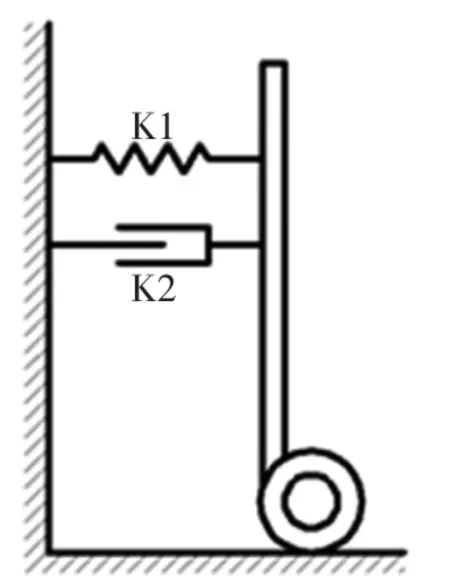
图4 两个系数对爬楼车平衡的作用模型Fig.4 Balance functional model about two coefficients of stairs-climbing vehicle

图5 爬楼车运动模型Fig.5 Self-balancing mechanical analysis model of stairs-climbing vehicle

在角度很小时，运动方程简化为：

车模静止时，a（t）=0，运动方程为：

通过建立等比例模型，验证了该种重心自平衡方法的可靠性。

3 结论

通过对现有行星式爬楼车的结构简化与改进，提出了一种新型 “全控式” 自平衡爬楼车的设计方案。增加了缓冲轮的，提高了爬楼车的爬升和缓冲能力，而且增加了自平衡控制该方案，通过理论上分析论证了设计的可行性，并进行了一定程度上的实际测试，效果较好。下一步需对爬楼与平地两种运行模式的自动转换进行研究。

[1] 苏和平，王人成.一种双联星形轮机构电动爬楼梯轮椅的设计[J].中国临床康复，2005，5.

[2] 王占礼.爬楼梯轮椅发展及关键技术的研究[J].机械研究与应用，2012，2.

[3] 刘祚时，等.基于ADAMS 的爬楼梯机器人动力学仿真[J].机床与液压，2010，23.

[4] 于苏洋，等.一种新型轮椅机器人爬越楼梯过程倾翻稳定性分析[J].中国机械工程，2010，22.

[5] 李超，等.一种轮组结构的爬楼梯轮椅的设计[J].现代机械，2010，6.

[6] 武明，等.新型爬楼爬楼车辆稳定性的灵敏度分析[J].甘肃工业大学学报，1998，1.

[7] 孟祥雨.一种星轮式爬楼梯电动轮椅设计与研究[D]. 长春工业大学，2012.

[8] 邓宗全，高海波，王少纯，等.行星轮式月球车的越障能力分析[J].北京航空航天大学学报，2004，3.

[9] 中华人民共和国国家计划委员会.GBJ101-87.建筑楼梯模数协调标准[S].北京：中国标准出版社，1987.