4种全球卫星导航系统实时动态定位效果评估
李博峰,项 冬
(同济大学测绘与地理信息学院,上海200092)
4种全球卫星导航系统实时动态定位效果评估
李博峰,项 冬
(同济大学测绘与地理信息学院,上海200092)
提出对流层去相关的实时动态定位(RTK)方法,有效降低单历元对流层参数与高程的相关性,实现对流层延迟与高程的有效分离,从而实现毫米级RTK定位.采用上海连续运行参考站(CORS)网的11条长度从23km到90km的基线,比较忽略对流层延迟与估计对流层延迟的单历元最小二乘解、动态卡尔曼滤波与对流层去相关4种RTK方法,重点分析对流层去相关RTK方法分离对流层参数与高程的效果,结果表明,对流层去相关方法在平面与高程方向定位精度均为毫米级,且高程相比平面精度更高.
全球导航卫星系统(GNSS);实时动态定位(RTK);亚厘米/毫米级定位;对流层去相关;卡尔曼滤波
在过去20年中,全球卫星导航系统(GNSS)实时动态定位(RTK)技术得到长足发展,并应用于诸多领域.为了实现高精度RTK定位,需要采用相位观测值并进行整周模糊度固定.当前,RTK方面的研究主要集中于模糊度固定方面[1-4],且RTK定位精度为厘米级已成为业内共识.尽管模糊度固定是RTK的关键,但它只是获取高精度定位的关键之一,对于模糊度固定后进一步提高RTK定位精度未引起学者的足够重视[5].
采用模糊度固定后的相位观测值进行高精度RTK定位可从两方面入手:一是引入外部约束或动态约束增加观测信息(如引入合理的动力学方程并采用卡尔曼滤波求解);二是对RTK定位模型中残余系统误差的有效处理[5-8].在实际应用中,构造合理的动态约束方程需要掌握载体的运动规律,过强且与载体运动规律不符的动态约束可能导致定位结果变差,因此,实际应用中构造的动力学方程都较保守,尤其在高动态情况下对定位解的贡献有限[9-10].在残余系统误差的处理方面,电离层与对流层是RTK定位的主要误差源,尽管电离层误差远大于对流层误差,但对双频或多频数据可通过无电离层组合观测值基本消除.因此,制约长基线RTK定位精度的主要因素是对流层误差[11].
在短基线定位中,由于空间误差的强相关性,双差后的对流层延迟可基本消除,因此,在短基线RTK中可忽略对流层的影响.而在中长基线定位中,通常引入对流层天顶延迟来吸收对流层误差的影响[12-14],但由于对流层参数和高程参数的相关性,一旦将对流层参数和坐标参数一起平差处理,将导致平差模型严重病态,通常需要积累足够的观测值以克服该病态问题,采用滤波方法或分段估计对流层延迟最小二乘解.然而,此类方法求解的对流层延迟实质上是多个历元对流层延迟的平均值,不能很好地反映对流层的实时变化信息.因此,理想的方法是单历元求解对流层和位置参数.为了克服单历元对流层参数与位置参数的强相关性,文献[5]提出了一种对流层去相关RTK方法,该方法有效降低单历元对流层参数与高程的相关性,实现对流层延迟与高程的有效分离,提高RTK定位的精度.
本文评估对流层去相关方法的RTK定位效果,采用上海连续运行参考站(CORS)网6个参考站构成11条长度从23km到90km的基线,比较分析忽略对流层延迟与估计对流层延迟的单历元最小二乘解、动态卡尔曼滤波与对流层去相关4种RTK方法的定位效果,并深入分析引起单历元RTK模型病态、各种方法定位误差的主要原因以及对流层去相关分离对流层参数与高程的效果.
1 数学模型与方法
1.1 基于无电离层组合观测值的RTK模型
模糊度固定后对应的无电离层组合RTK模型为

式中:ΦIF,PIF分别为模糊度固定后的双差无电离层伪距和相位组合观测值;Φ1,P1,f1分别为L1的双差相位和伪距观测值及频率;Φ2,P2,f2分别为L2的双差相位和伪距观测值及频率;x和τ分别为位置与相对天顶对流层延迟(RZTD)参数,对应的设计矩阵为A和g.模型(1)简写为
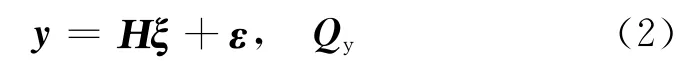
式中:y,H,ξ,ε,Qy分别为观测向量、设计矩阵、待估参数、观测噪声及其对应的协方差矩阵,QΦ和QP分别为双差无电离层相位和伪距组合协方差阵.
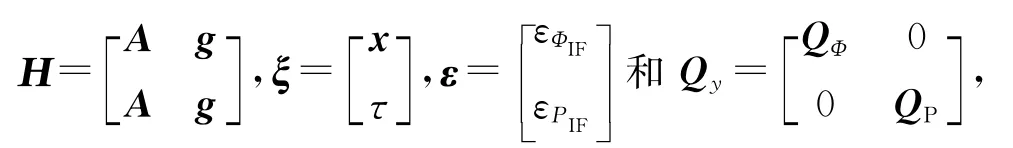
1.2 传统的RTK方法
传统的RTK方法包括忽略对流层延迟的单历元最小二乘解、估计对流层延迟的单历元最小二乘解以及卡尔曼滤波解.对于短基线RTK,由于空间误差的强相关性,双差对流层延迟可忽略,此时观测方程不再含有RZTD参数,相应地最小二乘定位解为

Φ方程;wx=ATQΦ-1ΦIF+ATQP-1PIF为法方程常数项;Q^x为最小二乘解的协方差阵.当残余对流层误差不足够小时,忽略RZTD 将导致定位解有偏,其偏差为

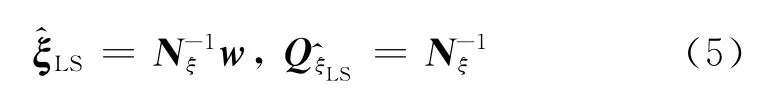
式 中:Nξ为 法 矩 阵,Nξ= HTQ-1yH =
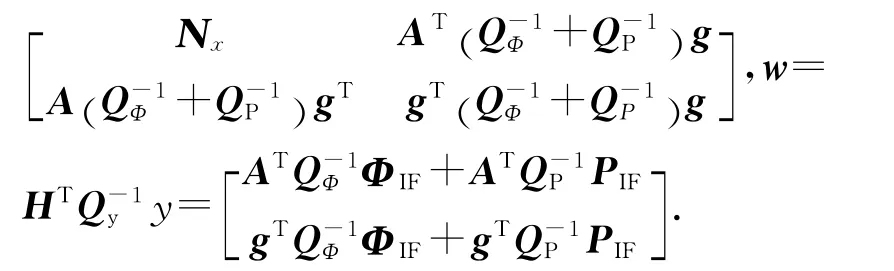
对流层延迟与高程分量强相关,因此模型(5)是病态的,此时单历元最小二乘解非常不稳定.为提高定位解的稳定性,通常将RZTD在一段时间内(如1 h)作为常数求解,或将RZTD参数作为随机游走过程引入如下动态约束方程:

式中:wτk为RZTD动态噪声;qτ为随机游走功率谱密度,通常取2~10cm2·h-1[14];Δt为历元间隔.引入动态约束后采用卡尔曼滤波求解,得

这3种传统的RTK方法都存在不同程度的缺陷.忽略对流层的最小二乘方法只适应于对流层误差足够小的短基线;而顾及对流层的单历元最小二乘解法的法方程严重病态,较小的误差将对结果产生较大的影响,有时甚至比忽略对流层的解效果还差;对流层误差的滤波处理尽管能有效地克服法方程的病态问题,但其本质是求解多个历元对流层误差的均值,因此无法反应出对流层误差的历元变化,从而无法有效吸收每个历元的对流层误差,因此最有效的方法就是能够将RZTD和位置参数单历元同时求解,这就需要研究有效克服RZTD和位置参数相关性的方法.
1.3 对流层去相关方法
观测方程(1)中位置设计矩阵A的高程分量和RZTD设计矩阵g都与卫星高度角有关,导致高程分量与RZTD对应的列向量呈严重的复线性相关性(见算例分析),高程分量与RZTD参数难以分离,从而法方程矩阵呈病态性[15],最小二乘解(5)不稳定.对于该病态问题文献[5]引入对流层去相关准则,即为最小.式中:下标R表示去相关解;常数α是去相关参数;正定矩阵M是去相关矩阵,取M=,则去相关解为

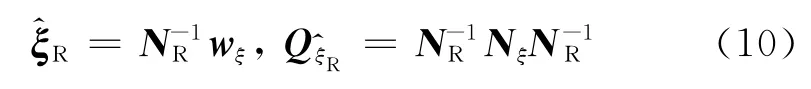
式中:NR=Nξ+αM.尽管去相关解比最小二乘解稳定,但去相关参数估计有偏,其偏差为=-,其中为参数的“真值”,但真值是未知的.因此,采用均方误差(MSE)评估顾及偏差影响的去相关解精度如下:

式中真值ξ-是未知的,通常采用最小二乘估值代替,但如果采用未迭代的最小二乘估值,由于其数值往往较大,导致α过小,难以起到去相关的效果;若采用迭代后的最小二乘估值,则由于其数值往往较小,导致α过大,从而估值偏差较大,因此,文献[5]提出采用最小二乘估值的协方差阵代替真值二阶矩阵的思想,该思想已被成功地应用于GNSS快速模糊度固定[1,16].在本文计算中取
将其代入式(11)并采用准则

求解去相关参数.式中trace表示求矩阵迹的运算.值得说明的是,协方差矩阵Qx^LS表征了卫星几何观测特性,因此计算的去相关参数随卫星几何观测强度自适应调节.得到合理的α后,对流层参数和高程之间的相关性就可以显著降低.对流层去相关方法能有效实现RZTD和位置参数的去相关,从而求解精确的单历元RZTD参数,有效吸收高时变的对流层误差,得到高精度的RTK结果.
2 试验与分析
为评估4种RTK方法的效果,采用上海连续运行参考站(CORS)网6个测站构成11条长度从23 km到90km的基线,数据为2010年7月18日双频GPS(global positioning system)数据,采样率为30 s,截止高度角10°,数据处理中采用UNB3对流层基本模型对观测数据进行改正.用Bernese软件处理6 d(每天24h)数据得到的静态网解作为真值,统计分析4种RTK方法的定位精度.设计4种RTK方案:方案A,忽略RZTD的单历元最小二乘解,式(3);方案B,估计RZTD的单历元最小二乘解,式(5);方案C,卡尔曼滤波估计位置和RZTD,式(7);方案D,对流层去相关的RTK方法,式(10).
首先,选取网中最长基线(约90km)比较分析4种RTK方案定位结果,该基线对应的几何精度因子(GDOP)和跟踪卫星数如图1所示,平均GDOP在2左右,平均跟踪卫星数约为8颗.4种方案的定位误差如图2所示,图中N,E和U 分别表示东 西、南北和高程3个坐标分量.4种方案RTK定位误差的均值(mean)、标准差(STD)和均方根误差(RMS)如表1所示,对定位结果分析如下:
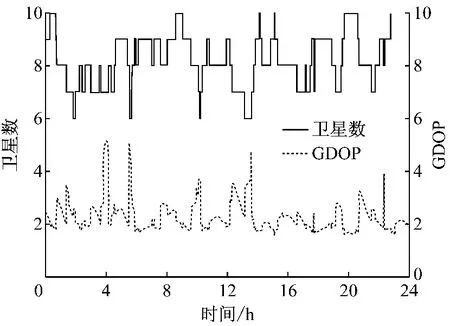
图1 卫星数与GDOPFig.1 Number of satellites and GDOP
(1)方案D的定位误差显然远小于其他3种方案,误差均值较其他方案更接近零,精度较其他方案更高,平面与高程精度都达到毫米级,且高程精度甚至优于平面精度,表明对流层去相关方法能有效地降低RZTD与高程的相关性,从而计算高精度的定位.图3给出了对流层去相关前后RZTD参数与高程的相关系数,显然在去相关前(即方案B),RZTD与高程几乎完全负相关,去相关后(即方案D)的RZTD与高程相关性明显改善.采用去相关方法不仅能提高定位精度,还可计算高精度的RZTD.为了分析去相关方法计算的RZTD,采用固定已知坐标用动态滤波估计的RZTD值作为参考,在此过程中取RZTD随机游走功率谱密度为3cm2·h-1.如图4给出了方案D求解得RZTD与参考值的比较,方案D求解的RZTD与参考值变化吻合,表明对流层去相关方法求解的RZTD能够很好地反映对流层随时间与环境的变化.

图2 4种RTK方案的定位误差比较Fig.2 Comparison of positioning errors for 4RTK schemes
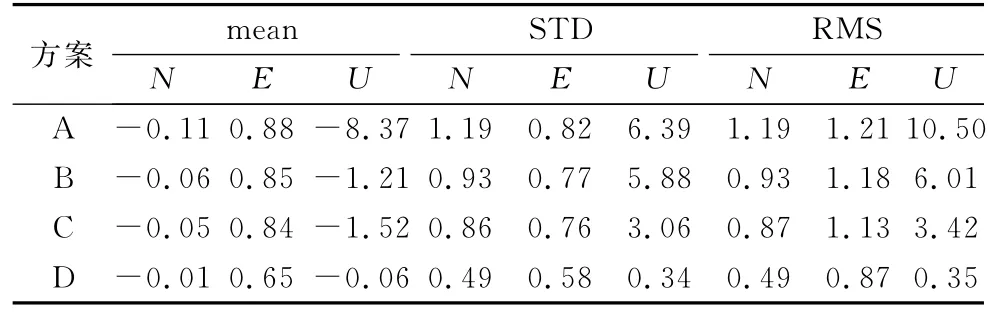
表1 4种RTK方案定位误差的统计结果Tab.1 Statistics(mean,STD and RMS)of positioning errors of 4RTK schemes cm

图3 去相关后位置分量与RZTD相关系数比较Fig.3 Comparison of correlation coeficients between height component and RZTD after decorrelation
(2)采用卡尔曼滤波解的方案C优于方案A和B,方案C中动态滤波效果与RZTD动态噪声取值有关,当动态噪声无穷大时滤波模型退化为方案B的单历元解,若动态噪声过小则可能导致模型难以反映RZTD随时间的变化,试验取RZTD随机游走功率谱密度为3cm2·h-1.比较图4中方案C的RZTD值与参考值可知,方案C计算的RZTD变化平稳,其变化趋势与参考真值基本一致但不完全吻合,解释了方案C定位误差变化.尽管方案A误差小于方案B,但由于方案A忽略了RZTD,定位结果明显存在系统误差,特别是在高程方向,系统误差更为明显.式(4)给出了方案A的定位偏差Δx^=sτ-,表征忽略对流层延迟引起的模型偏差与定位系统几何结构有关.由式(4)可知方案A的定位系统误差由RZTD与偏差向量共同确定,图5给出了N,E和U 3个方向的敏感因子,高程的敏感因子远大于平面分量,平均值约为-3,表明高程误差量级为RZTD的3倍.结合图4中RZTD参考值变化(8h后RZTD逐渐变化)解释了方案A高程定位误差在8h后迅速增大的原因.
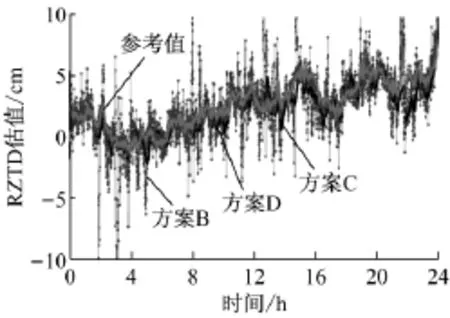
图4 3种RTK方案的RZTD值与参考值比较Fig.4 Comparison of RZTDs from 3RTK schemes with their references
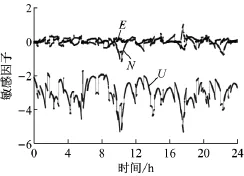
图5 模型偏差敏感因子Fig.5 Sensitive factors of model errors
(3)方案B估计了RZTD参数,定位结果没有系统性误差,但由于单历元RZTD与高程的强相关导致模型(5)严重病态,从而定位精度非常差,特别是高程方向,精度达到6cm.为了分析RZTD和高程相关性的原因,将位置参数从WGS84坐标系转化为站心坐标系(NEU),即

理论上,sinθ=ΔU/ρ,其中θ为高度角,ρ为卫地距.为简化讨论,取对流层延迟映射函数为高度角的反正弦函数1/sinθ.图6给出了θ>30°时高程分量与RZTD系数,不难看出高程分量与RZTD系数的复线性相关程度与θ有关;当θ>60°时,高程和RZTD参数的系数变化几乎相同,说明此时高程与RZTD参数几乎线性相关.由此可知,高程分量与RZTD存在较强的复线性关系从而导致模型病态.单历元同时估计位置与RZTD参数可得到无偏估值,但病态方程中观测值的微小扰动都可导致较大的偏差,试验结果表明方案B的解非常不稳定(图2b).
为进一步分析4种RTK方案的定位能力,处理了CORS网6个测站构成的11条基线数据,统计各方案定位误差的均值与RMS.如图7所示,方案A, B,C在平面方向定位误差均值与RMS相差不大,均优于2cm.由于考虑了对流层延迟的历元间动态约束,卡尔曼滤波解(方案C)定位结果优于方案A和B.方案A定位精度总体优于方案B,但定位解有偏的,尤其在高程方向偏差更为明显,当基线较长时高程定位精度甚至不如方案B.特别值得指出的是,对于23km至90km的基线,对流层去相关方法得到的平面与高程定位精度始终为毫米级,明显优于其他方案,说明对流层去相关的RTK方法是稳健有效的.
'
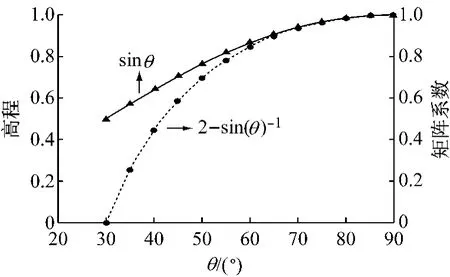
图6 高程分量与RZTD设计矩阵系数的比较Fig.6 Comparison of coefficients between hight component and RZTD from design matrices
3 结论
为了进一步提高长距离RTK定位精度,需要严格考虑对流层延迟的影响,并采用合理的数据处理方法求解高精度高分辨率的对流层延迟参数.针对RZTD和高程分量强相关引起的RTK模型病态问题,采用了对流层去相关方法降低了RZTD和高程的相关性,有效地分离RZTD和位置参数,从而获得毫米级的RTK定位解.本文采用GPS实际数据深入分析了当前4种RTK方法的定位效果,得出结论如下:
(1)忽略对流程层延迟将在高程方向引入相当于RZTD 3倍的定位误差,因此长距离RTK定位中需要引入RZTD参数吸收对流层误差的影响;然而,尽管引入RZTD能有效地消除对流层系统误差的影响,但由于RZTD参数与高程分量的强相关性,导致RTK定位精度更差.
(2)卡尔曼滤波考虑了RZTD动态约束信息,可在一定程度上提高定位精度,但由于卡尔曼滤波求解的RZTD不能反映对流层的细节变化,定位精度充其量达到平面1cm左右、高程3cm左右.
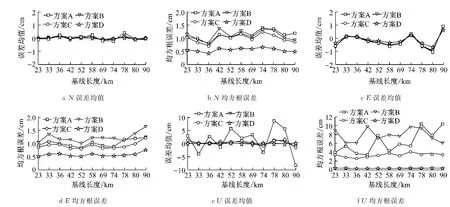
图7 11条基线4种RTK方案的定位误差的统计结果Fig.7 The statistics(mean and RMS)of positioning errors by 4RTK schemes for 11baselines
(3)采用对流层去相关方法能够有效地降低RZTD与高程分量的相关性,从而改善单历元RTK方程病态性,单历元求得的RZTD能反映出对流层的细节性变化特征,从而实现平面与高程均为毫米级精度的RTK定位效果.值得指出的是,本文采用无电离层模型并通过双差观测值消除其他误差的影响,对双差后残余系统误差的处理有待进一步研究.
[1] LI Bofeng,SHEN Yunzhong,FENG Yanming.Fast GNSS ambiguity resolution as an ill-posed problem[J].Journal of Geodesy,2010,84(11):683.
[2] LI Bofeng,SHEN Yunzhong,FENG Yanming,et al.GNSS ambiguity resolution with controllable failure rate for long baseline network RTK[J].Journal of Geodesy,2014,88(2):363.
[3] LI Xingxing,ZHANG Xiaohong,GE Maorong.Regional reference network augmented precise point positioning for instantaneous ambiguity resolution[J].Journal of Geodesy,2011,85(3):151.
[4] ZHANG Xiaohong,LI Pan.Assessment of correct fixing rate for precise point positioning ambiguity resolution on a global scale[J].Journal of Geodesy,2013,87(6):579.
[5] LI Bofeng,FENG Yanming,SHEN Yunzhong,et al.Geometry-specified troposphere decorrelation for subcentimeter real-time kinematic solutions over long baselines[J].Journal of Geophysical Research:Solid Earth,2010,115(B11404),doi:10.1029/2010JB007549.
[6] Odijk Dennis.Weighting ionospheric corrections to improve fast GPS positioning over medium distances[C]∥ION GPS 2000.Salt Lake City:[s.n.],1113:19-22.
[7] Wielgosz P,Kashani I,Grejner-Brzezinska D.Analysis of long-range network RTK during a severe ionospheric storm[J].Journal of Geodesy,2005,79(9):524.
[8] Zhang Jihong,Lachapelle G.Precise estimation of residual tropospheric delays using a regional GPS network for real-time kinematic applications[J].Journal of Geodesy,2001,75(5-6):255.
[9] YANG Yuanxi,HE Haibo,XU Guchang.Adaptively robust filtering for kinematic geodetic positioning[J].Journal of Geodesy,2001,75(2-3):109.
[10] ZHOU Zebo,LI Bofeng.GNSS windowing navigation with adaptively constructed dynamic model[J].GPS Solutions,2015,19:37.
[11] LI Bofeng,FENG Ynming,SHEN Yunzhong.Three carrier ambiguity resolution:Distance-independent performance demonstrated using semi-generated triple frequency GPS signals[J].GPS Solutions,2010,14(2):177.
[12] Kim D,Bisnath S,Langley R,et al.Performance of longbaseline real-time kinematic applications by improving tropospheric delay modeling[C]∥ION GNSS 2004.Long Beach:[s.n.],2004:21-24.
[13] Ahn Y,Kim D,Dare P.Estimation of troposphere decorrelation using the combined zenith-dependent parameter[C]∥ION GNSS 2008.Savannah:[s.n.]:2008:16-19.
[14] 葛茂荣,刘经南.GPS定位中对流层折射估计研究[J].测绘学报,1996,25(4):285.GE Maorong,LIU Jingnan.The estimation methods for tropospheric delays in global positioning system[J].Acta Geodaetica et Cartographica Sinica,1996,25(4):285.
[15] OU Jikun,WANG Zhenjie.An improved regularization method to resolve integer ambiguity in rapid positioning using single frequency GPS receivers[J].Chinese science bulletin,2004,49(2):196.
[16] 李博峰,沈云中.顾及基线先验信息的GPS模糊度快速解算[J].测绘学报,2008,37(4):423.LI Bofeng,SHEN Yunzhong.Prior baseline information based fast GPS ambiguity resolution[J].Acta Geodaetica et Cartographica Sinica,2008,37(4):423.
Evaluation and Comparison of Four Methods for Global Navigation Satellite Systems Real-time Kinematic Positioning
LI Bofeng,XIANG Dong
(College of Surveying and Geo-Informatics,Tongji University,Shanghai 200092,China)
The troposphere decorrelation method was proposed,which can effectively decrease the correlation of tropospheric parameter and height of single epoch,thus realizing the efficient decouple of height and tropospheric delay and then the millimeter RTK(real-time kinematic)results.In this paper,we evaluate the performance of 4 RTK methods by using 11 baselines with baseline lengths from23 km to 90 km from Shanghai Continuously Operation Reference Station(CORS)network,including the single epoch least squares solutions with and without tropospheric delays,the kinematic Kalman filtering solution and the troposphere decorrelation solution.We highlight the analysis of RTK performance from the troposphere decorrelation method.The numerical experiments indicate that the millimeter accuracies can be obtained for all three coordinate components in the RTK solutions by the troposphere decorrelation method.
global navigation satellite systems(GNSS);real time kinematics(RTK);subcentimeter/millimeter positioning;troposphere decorrelation;Kalman filtering
P228.4
A
0253-374X(2015)12-1895-06
10.11908/j.issn.0253-374x.2015.12.020
2014 10 09
国家自然科学基金(41374031;41574023);国家测绘与地理信息局公益性专项(HY14122136)
李博峰(1983—),男,教授,博士生导师,工学博士,主要研究方向为测量数据处理和GNSS理论与应用.E-mail:bofeng_li@tongji.edu.cn

