Model algorithm control using neural networks for input delayed nonlinear control system

Yuanliang Zhangand Kil To Chong

1.School of Mechanical Engineering,Huaihai Institute of Technology,Lianyungang 222005,China;

2.School of Electronics and Information,Chonbuk National University,Jeonju 560756,South Korea

Model algorithm control using neural networks for input delayed nonlinear control system

Yuanliang Zhang1and Kil To Chong2,*

1.School of Mechanical Engineering,Huaihai Institute of Technology,Lianyungang 222005,China;

2.School of Electronics and Information,Chonbuk National University,Jeonju 560756,South Korea

The performance of the model algorithm control method is partially based on the accuracy of the system’s model.It is diffcult to obtain a good model of a nonlinear system,especially when the nonlinearity is high.Neural networks have the ability to“learn”the characteristics of a system through nonlinear mapping to represent nonlinear functions as well as their inverse functions.This paper presents a model algorithm control method using neural networks for nonlinear time delay systems.Two neural networks are used in the control scheme.One neural network is trained as the model of the nonlinear time delay system,and the other one produces the control inputs.The neural networks are combined with the model algorithm control method to control the nonlinear time delay systems.Three examples are used to illustrate the proposed control method.The simulation results show that the proposed control method has a good control performance for nonlinear time delay systems.

model algorithm control,neural network,nonlinear system,time delay.

1.Introduction

Time delay is a common phenomenon encountered in the analysis and design of control systems.Systems with time delays exhibit complex behaviors because of their infnite dimensionality[1].Time delay occurs within many engineering systems,such as chemical processes and rolling mill systems[2].In recent years,the analysis and synthesis problems for systems subject to time delays have attracted the interests of many researchers[3,4].Zhu et al. [5]presented suffcient conditions for the stability of linear time delay systems based on two-dimensional hybrid polynomials while Zeng et al.[6]dealt with the problem of stability for systems with the interval delay.Sun et al.[7] addressed the problem of stability analysis and stabilization for discrete-time singular delay systems,and designed the state feedback controller.Zhou et al.[8]concerned with the observer based output feedback control of linear systems with both input and output delays.

Most of the control methods listed above are based on linear systems.However,almost all control systems exhibit nonlinear characteristics.If the plant is nonlinear and there are disturbances during the control process,it becomes diffcult to use a linear based control strategy to obtain a satisfactory control performance.Therefore,it is important to study controller design based on nonlinear system models. Time delay compensation techniques which employ nonlinear models can improve the performance of nonlinear systems.However,only a few nonlinear time delay compensation strategies exist[9].Song et al.[10]proposed an iteration algorithm to solve the fnite horizon optimal control problem for nonlinear time delay systems.Chen[11] designed a nonlinear fuzzy controller for time delay tension leg platform(TLP)systems.Xiang et al.[12]presented the robust reliable control problem for uncertain stochastic switched nonlinear systems under asynchronous switching with delays.The problems of robust stabilization of uncertain stochastic,switched nonlinear systems and discrete-time switched nonlinear systems with time delays under asynchronous switching are considered in[13,14]. Liu et al.[15]dealt with the problems of stability and control for uncertain nonlinear systems with state delays.Tong et al.[16]presented two adaptive neural network decentralized output feedback control methods for uncertain nonlinear systems with unknown time delays.

Previously,a model algorithm control(MAC)method for nonlinear time delay systems was proposed in[17].For the MAC based control system,an accurate plant model is necessary to obtain a good performance.However,in practice,most plants have nonlinear characteristics causing diffculty in obtaining the good model of the nonlinear sys-tem.In this case,the MAC controller cannot be designed. The neural network control scheme had been shown to be particularly useful for the control of nonlinear systems owing to the neural network’s excellent function approximation ability[18].Chen et al.[19]addressed the problem of adaptive control for nonlinear systems with delays using neural networks.The neural network was employed to compensate for the unknown nonlinear terms.Liu et al. [20]proposed an adaptive controller for nonlinear single input single output(SISO)systems with partial unmeasured states using neural networks.Qiu et al.[21]developed the vibration control method for a fexible piezoelectric beam using a back propagation(BP)neural network. The neural network was trained to update the parameters of the proportional integral derivative(PID)controller.Han et al.[22]used a BP neural network to adjust the parameters of the PID controller and applied it to the main steam temperature control in the power plant.In this paper,two BP neural networks are combined with MAC to provide control signals for nonlinear time delay systems.These two neural networks are trained to estimate the model and inverse model of the system.Afterwards,the MAC method can be designed based on these two neural networks.

In particular,this paper makes the following contributions.

(i)The closed-loop MAC control method has a high degree of robustness against process models since the process uncertainties can be incorporated by adjusting discrepancies between the process output and its predicted value. The proposed neural network MAC(NNMAC)possesses this advantage of the MAC method.

(ii)Time delays may worsen the performance of the system,and even cause the system unstablity.The proposed NNMAC method can be applied to nonlinear systems with time delays and can provide good and robust control results.

(iii)It is diffcult to obtain the model of nonlinear systems,especially when the nonlinearity is high.Neural networks have the ability to“learn”system characteristics to represent arbitrary nonlinear functions and their inverse functions and provide a stronger degree of robustness due to their ability to exhibit fault tolerance.In Section 3,the method that deals with nonlinear time delay systems when training the neural network is introduced.In the proposed NNMAC method two neural networks are used:one is trained to estimate the nonlinear time delay system and the other one is trained to provide the control input signals.

This paper consists of the following sections to explain the results of the study.Section 2 presents MAC for nonlinear time delay systems while information regarding the neural networks and their applications within the NNMAC method are shown in Section 3.Computer simulations of the proposed controller for the nonlinear time delay system are presented in Section 4.Finally,the conclusions are drawn in Section 5.

2.MAC for nonlinear time delay systems

2.1State space formulation of MAC for linear systems

A linear system can be described by the following model:

Here the subscript m is added to explicitly indicate that xmand ymrepresent estimates of x and y,respectively.This notation helps differentiate ymfrom the measured output, which is still denoted by y.Suppose that CAiB=0 (i=0,1,...,r−2)and CAr−1B/=0.r is the relative order of the system,i.e.r is the smallest number of sampling periods after which the input u affects the output y.The model of(1)can be simulated to predict the future behavior of the system.In particular,from the model described by(1),we obtain:

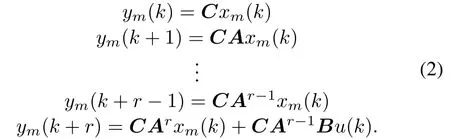
The future changes in the output can be predicted as

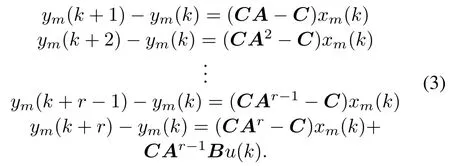
These predicted changes shown in(3)with the addition of the measured output signal y,can be used to obtain the future predictions of the output,which is shown in(4).

where the superscriptˆis used to represent the prediction of the output y.It is interesting to observe that the output predictions in(4)are“closed loop”in the sense that they make use of the measured output signal.

Then,the question that arises is what the choice of u(k) should be in order to obtain a desirable output response. If u(k)is chosen so thatˆy(k+r)is exactly the set pointvalue ysp(k),this would clearly create a non-robust situation.Instead,one can requestˆy(k+r)to be in the right direction and cover a fraction of the“distance”between ˆy(k+r−1)and ysp(k).In other words,one can defne a desirable value ydof the output at the(k+r)th time step by

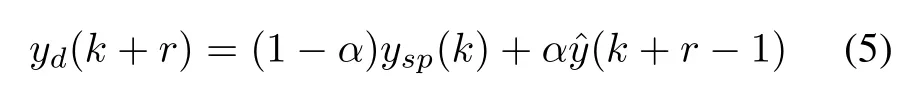
where α(0＜α＜1)is a tunable flter parameter.Clearly α→0 corresponds to yd(k+r)→ysp(k),and trying to force the output to go to the set point as soon as possible; whereas α→1 corresponds to yd(k+r)→ˆy(k+r−1), leaving the output unaffected.An intermediate choice of α corresponds to a desirable value of the output between ysp(k)andˆy(k+r−1)that tries to bridge the gap to a certain extent.The choice of α is decided by the target of the control system and the characteristics of the plant.If α is chosen as a large one,the robust situation of the control system will be good.At the same time,the velocity of the system to track the set point will be slow.On the other side,if α is a small one,the control system will track the set point fast,but the control system will be sensitive to the disturbances.Usually,frst a large value of α can be chosen,then reduce it gradually until a satisfactory control performance is obtained.Equation(5)is referred to as the“reference trajectory”.

Once the reference trajectory has been specifed,the question becomes how to choose the control input u(k)so thatˆy(k+r)will match yd(k+r).This can be formulated as an optimization problem:

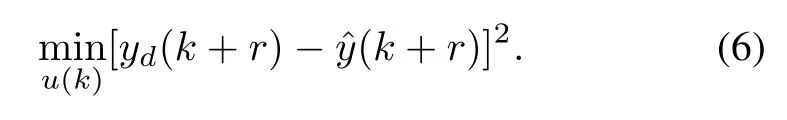
Consider(4)and(5),we can get

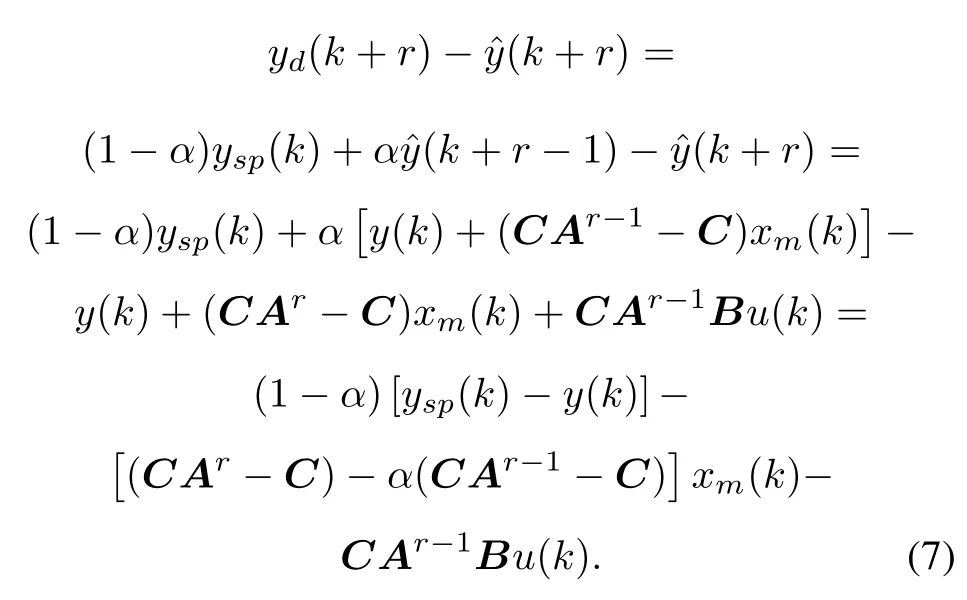
Let e(k)=ysp(k)−y(k),then(6)can be rewritten as

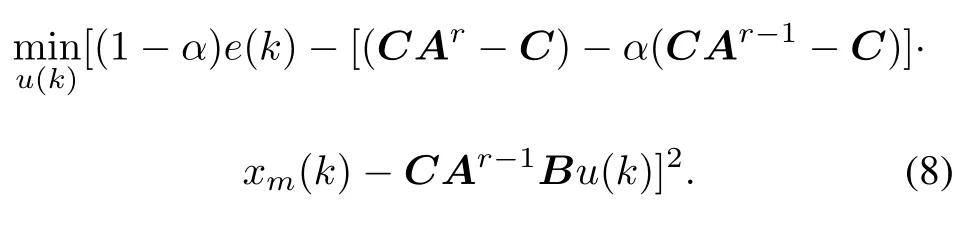
The solution of(8)is the derived control law for the linear system to be controlled.

2.2MAC for nonlinear systems

The description of the linear MAC presented in the previous subsection can be extended to nonlinear systems which can be described by the discrete time model:

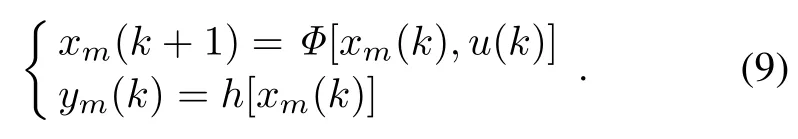
Suppose that(9)has the relative order r.This means that:

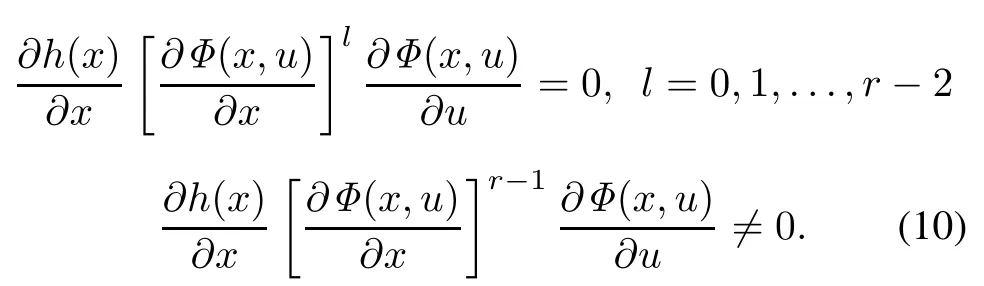
Assume that

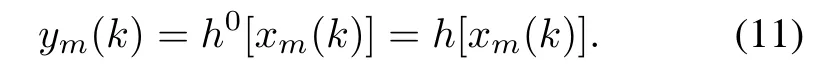
Based on(9)and(11)we have

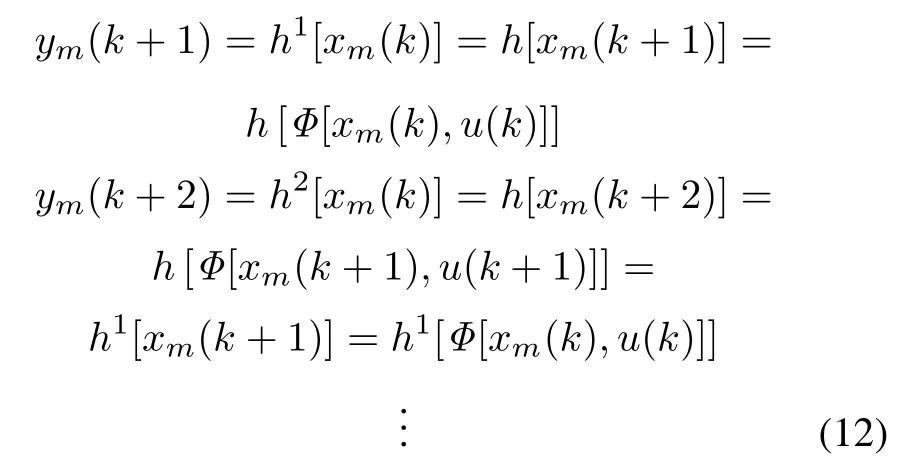
Then we have the following notation:

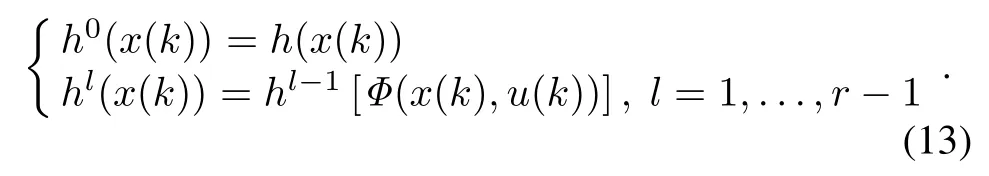
The output y future changes can be predicted using the discrete time model shown in(9).

Since(9)has the relative order r,the following equation is true.

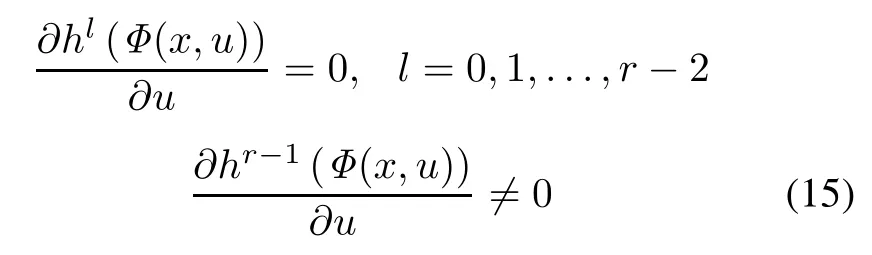
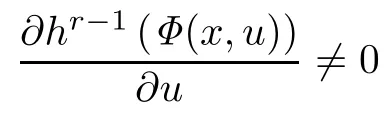
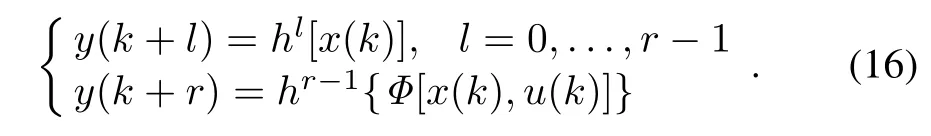
is locally solvable in u,and can be expressed by(18).

Here(18)is assumed to be well defned and unique on X×h(X).

By adding the predicted output changes shown in(14) to the measured output y,the following“closed loop”predictions of the output can be obtained.

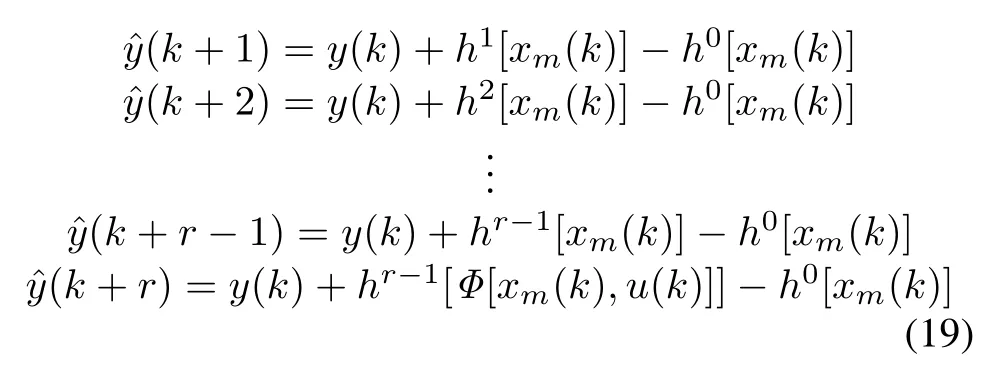
Defning a reference trajectory in the same manner as in the linear case,a nonlinear model algorithm controller can be derived by requesting the output prediction to match the reference trajectory.Considering(5)and(19),we can get that yd(k+r)=(1−α)ysp(k)+αˆy(k+r−1), ˆy(k+r−1)=y(k)+hr−1[xm(k)]−h0[xm(k)],and ˆy(k+r)=y(k)+hr−1[Φ[xm(k),u(k)]]−h0[xm(k)]. After replacing yd(k+r),ˆy(k+r−1)andˆy(k+r)in (6),with these equations,(6)becomes

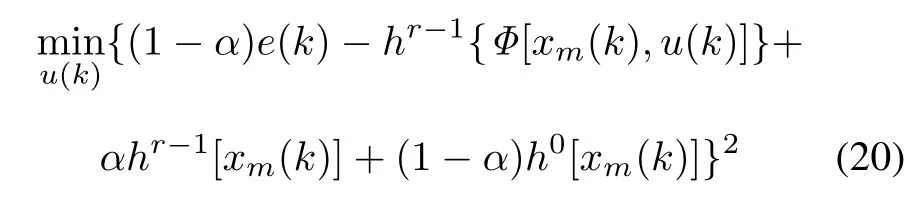
where e(k)=ysp(k)−y(k).

Minimizing(20)is the solution of the nonlinear equation:

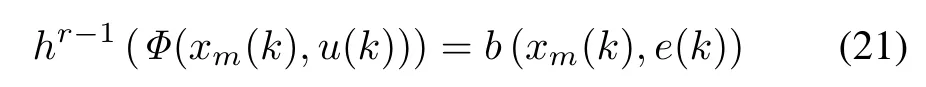
Considering the defnition of Ψ0shown in(18),the solution can be represented as

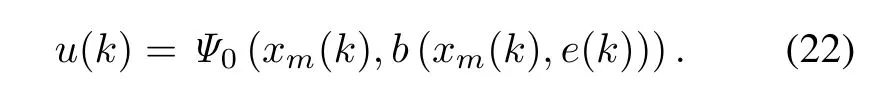
3.MAC using neural networks

In the NNMAC method,two neural networks,NN1 and NN2,are used.NN1 and NN2 are trained to estimate the model and inverse model of the nonlinear time delay system,respectively.NN1 and NN2 are both BP neural networks.Fig.1 shows the confguration of the BP neural network.The structure of the two neural networks is the NNARX(autoregressive external input)model structure. The NNARX model structure is presented in(23).

where g is the function realized by the neural network,x is the system’s output,u is the control input,xmis the neural network output and dT is the delay time of the nonlinear system(T is the sampling period).The parameters a and c are the numbers of past data of the system outputs and inputs,respectively.How to select the inputs of NN1 and NN2 is an important problem that must be solved.On the one hand if the number of the inputs is chosen very small the neural network will be underft.In this case,the neural network cannot estimate the system well.On the other side,if the number of the inputs is chosen very large although the accuracy can be improved,the training of the neural network will become very complicated.In order to obtain the right number of the inputs,a lot of times of training and test using various numbers of the inputs must be conducted.

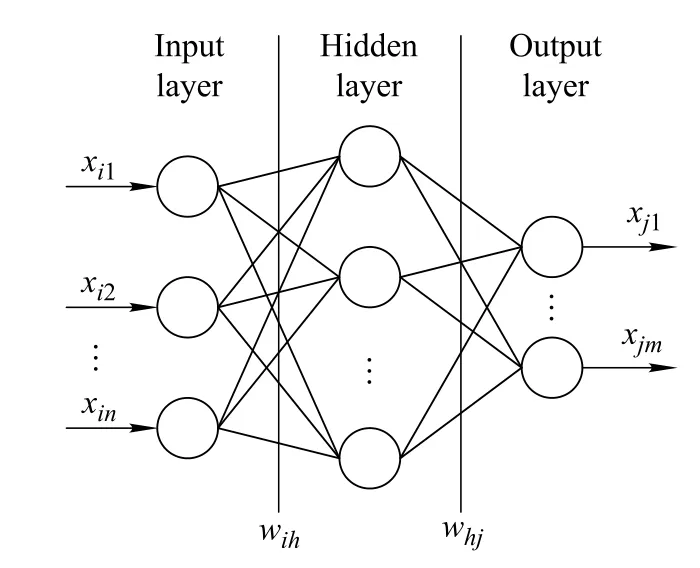
Fig.1 Confguration of BP neural networks

NN1 is trained by offine training.The experiment is frst conducted to get the training and test data.In the experiment,the input signal u will be designed carefully in order to cover all of the operating range of the system.For example the input signal u can be designed using(24), which is shown in Fig.2.After doing the experiment,a series of input signals u and the corresponding system’s output x are obtained.The half of the data gotten is used as the training data,and the rest of the data is used as the test data.For the system in Example 1,at the beginning a small number of the inputs are used,then gradually the number increases and the errors of NN1 are checked.After trying several times it is found that a=3 and c=3 arethe best choices.Particularly,NN1 has six neurons in the input layer and six neurons in the hidden layer.The transfer functions of the hidden layer and the output layer are fh(x)=tanh(x)and fo(x)=x,respectively.The inputs of NN1 are[x(k−1),x(k−2),x(k−3),u(k−d−1),u(k−d−2),u(k−d−3)]and the output of NN1 is xm(k). Fig.3 shows the structure used to train NN1.

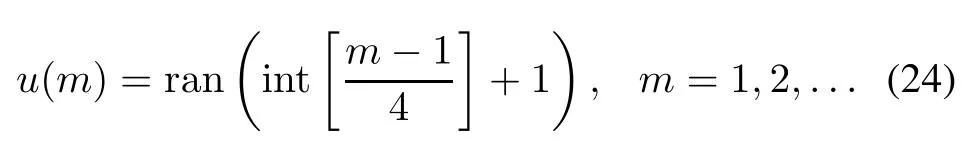
where ran(·)is a kind of uniformly distributed random number and int[·]denotes the integer part.

Fig.2 Experiment of the input u

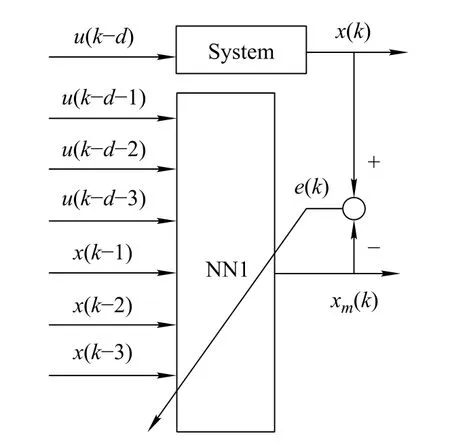
Fig.3 Structure used to train NN1

The process of deciding the number of the input layer neurons of NN2 is similar with that of NN1.The transfer functions of the hidden layer and the output layer are fh(x)=tanh(x)and fo(x)=x,respectively.The output and previous input data of the system act as the inputs of NN2.And the output of NN2 is the estimation of the present input data,u′(k),of the system.For the nonlinear time delay system,the training of NN2 is more complicated than that of NN1.The principle for handling time delays is outlined as follows[23].

Assume that the system is governed by

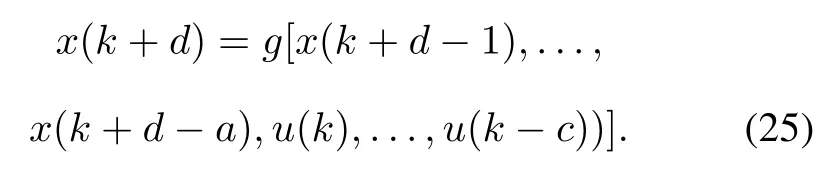
Then,the input u can be expressed as

Considering MAC presented in Section 2,x(k+d)is substituted for b[xm(k),e(k)]and d−1 unknown quantities({x(k+1),...,x(k+d−1)})are left.In the simulation section,the system’s time delay is d=2.In this case, there will be one unknown quantity,namely x(k+1).The prediction of this unknown quantity takes the form:

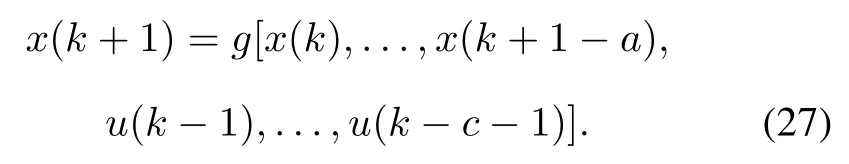
Considering(25)and(26),we can obtain the expression of u(k)as follows:

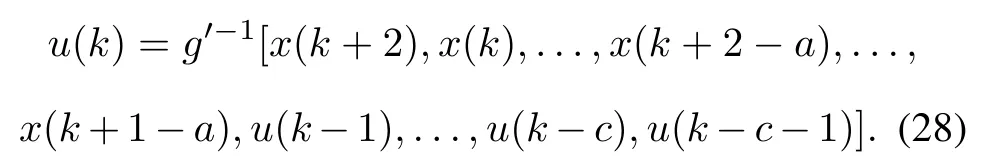
The controlled system’s input data shown in Fig.2 and the corresponding output data are used as the training and test data for NN2.Particularly,for NN2 in Example 1 we choose eight neurons in the input layer and eight neurons in the hidden layer.The inputs of NN2 are [x(k+2),x(k),x(k−1),x(k−2),x(k−3),u(k−1),u(k−2),u(k−3)]and the output of NN2 is u′(k).Fig.4 shows the structure used to train NN2.

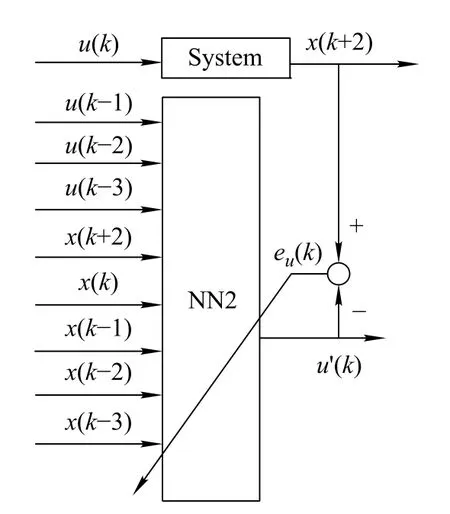
Fig.4 Structure used to train NN2

The Levenberg-Marquardt method is used to train NN1 and NN2.Analogizing to the MAC method,in the NNMAC method two neural networks,NN1 and NN2,are used to do the control job.In this case,it is assumed that the model and inverse model of the controlled system are hard to be obtained.This means that(9)and(18)are unknown. NN1 is trained to estimate the controlled system’s model to generate xm(k),and NN2 is trained to estimate the inverse model of the controlled system.The well trained NN1 andNN2 can be used to form the NNMAC control scheme.The diagram of the proposed control system is shown in Fig.5. b[xm(k),e(k)]=α hr−1(xm(k))+(1−α)(h(xm(k))+ e(k))is used to calculate the value of b[·].Analogizing to the MAC method,NN1 provides the estimation of the controlled system’s state,xm(k).Referring(18)and(22),and by using b[xm(k),e(k)]to go through NN2,NN2 can do the same job of(22)to provide NNMAC’s control input for the nonlinear time delay system.

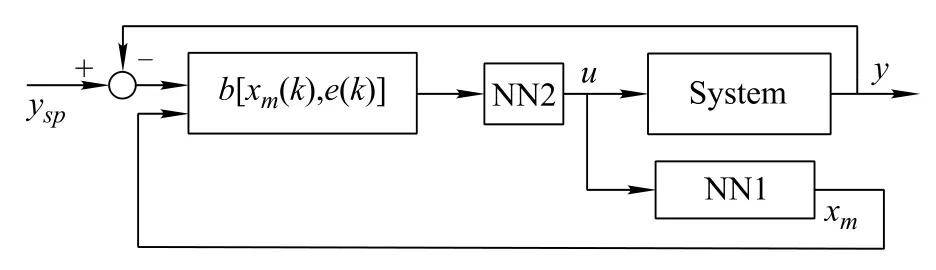
Fig.5 Principle of NNMAC control system

Remark 1The proposed NNMAC control scheme employs two neural networks.NN1 is trained to estimate the system and NN2 is trained to provide the control input signals.Since neural networks can learn nonlinear characteristics of the system and are robust due to its fault tolerance ability,the proposed NNMAC method can be applied to the complex nonlinear system whose model cannot be obtained easily,while the traditional MAC method cannot work.

Remark 2The proposed NNMAC control scheme keeps the advantage of the MAC method,high degree of robustness against process models uncertainties.And it can also be applied to the systems with time delays.In this paper,the NNMAC method is applied to the SISO nonlinear time delay system and its extension to the multiple-input multiple-output(MIMO)nonlinear time delay system is also feasible.

4.Simulation

Control systems with time delays exhibit complex behavior because of their infnite dimensionality.The time delay factors have counteracting effects on the system behavior and most of the time this leads to poor performances. The existence of time delays in practical systems may induce instability and oscillations in a large number of important physical and industrial engineering applications. Ignorance of time delays in the design of the control system may lead to unpredictable and unsatisfactory system responses,especially for nonlinear systems.In this paper,the time delay is considered in the proposed NNMAC method.The details about dealing with the time delay in the neural networks are shown in Section 3.The performance of the proposed NNMAC method is evaluated by the following examples.

Example 1Consider a CSTR model for a chemical reactor system[24].CSTR is a general nonlinear chemical process and the equation of the model can be expressed by

First NN1 and NN2 are trained to estimate the model and inverse model of the system using the structures presented in Section 3.Here Matlab Simulink Toolbox is used to do the experiment to obtain the training and test data. The sampling period is chosen as T=0.1 s.The absolute values of the training and test errors of NN1 and NN2 are shown in Figs.6 and 7,respectively.The mean squared errors of NN1 for training and test results are 1.057×10−8and 8.542×10−9,respectively.The mean squared errors of NN2 for training and test results are 3.032×10−6and 2.648×10−6,respectively.The well trained NN1 and NN2 can be used to form the neural network model algorithm controller for the controlled system.In the simulation the“System”shown in Fig.5 is realized using Matlab Simulink Toolbox.

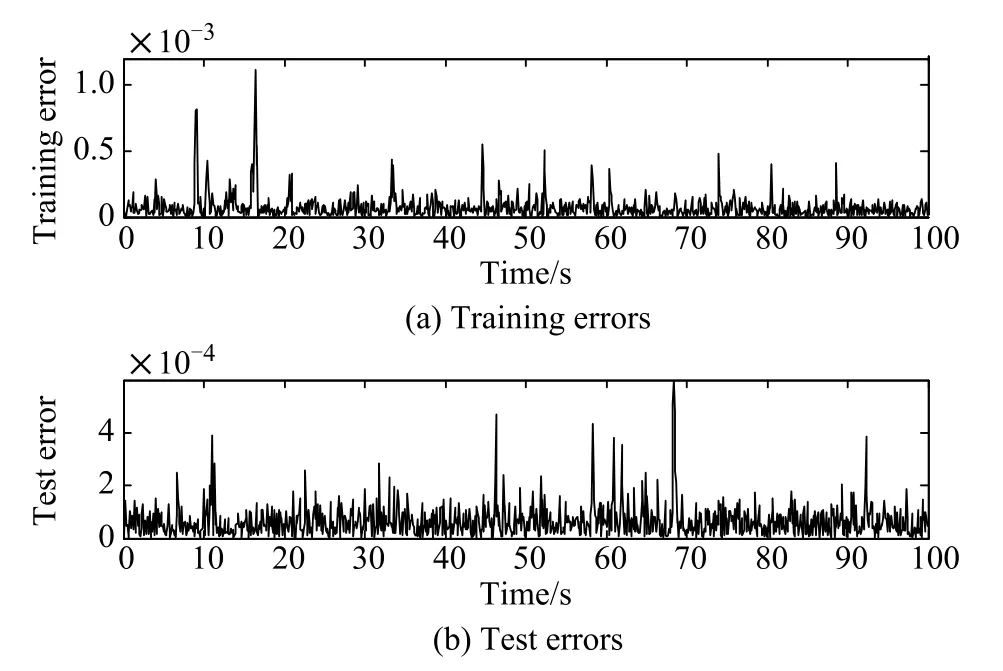
Fig.6 Training and test errors of NN1

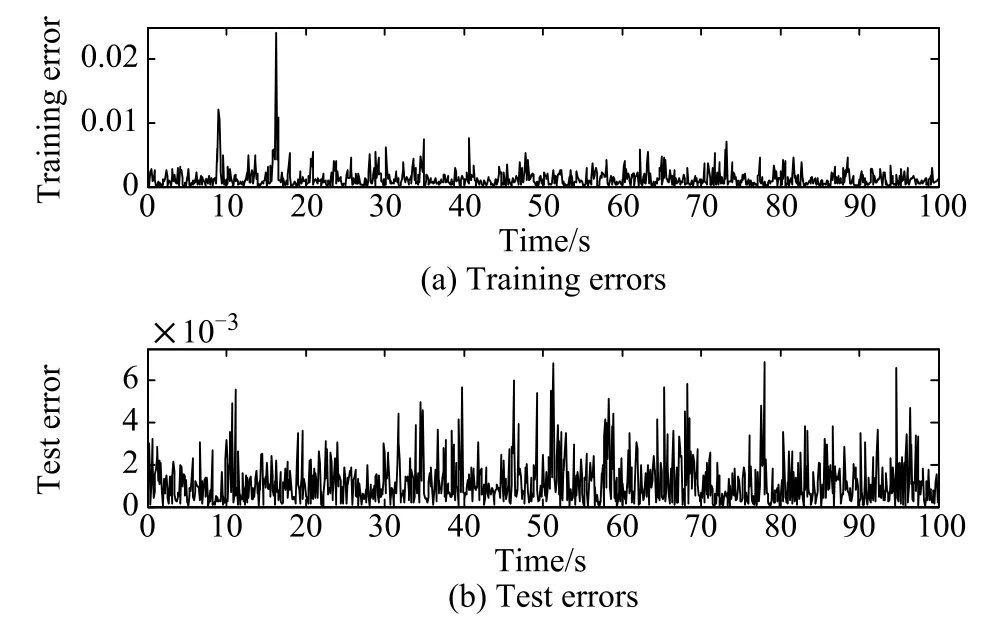
Fig.7 Training and test errors of NN2

At frst,we choose the initial value x(0)=0.02,the sampling period T=0.1 s and the time delay D=0.1 s. A nonlinear inverse controller is employed to make thecomparison with the proposed NNMAC method.α is set as 0.9.Fig.8 shows the reference signals,the control system’s outputs,and the control inputs.

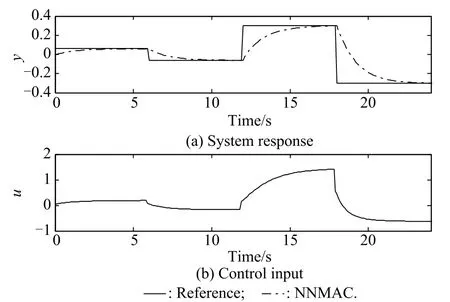
Fig.8 System response and control input using NNMAC method (D=0.1 s,α=0.9)

Fig.8 shows that since α is quite large the system outputs follow the reference signals very slowly.It is obvious that α=0.9 is not a good choice.Then,we reduce α gradually.Fig.9 shows the reference signals,the control system’s outputs,and the control inputs when α=0.7.Then α=0.5 is used.In this case,a nonlinear inverse controller is also used to do the simulation in order to make the comparison with the proposed NNMAC method.Fig.10 shows the reference signals,the control system’s outputs using the two nonlinear controllers and the control inputs when α=0.5.

Figs.8–10 show that as α reduces,the system output will follow the reference signal more quickly,and at the same time,the control input will be larger.α can be chosen according to the control requirements and the characteristics of the controlled system.In this case α=0.5 is good enough.Fig.10 shows the comparison results between the proposed NNMAC method and a nonlinear inverse controller.From Fig.10,it can be seen that the proposed NNMAC method can provide better control results than the nonlinear inverse controller.

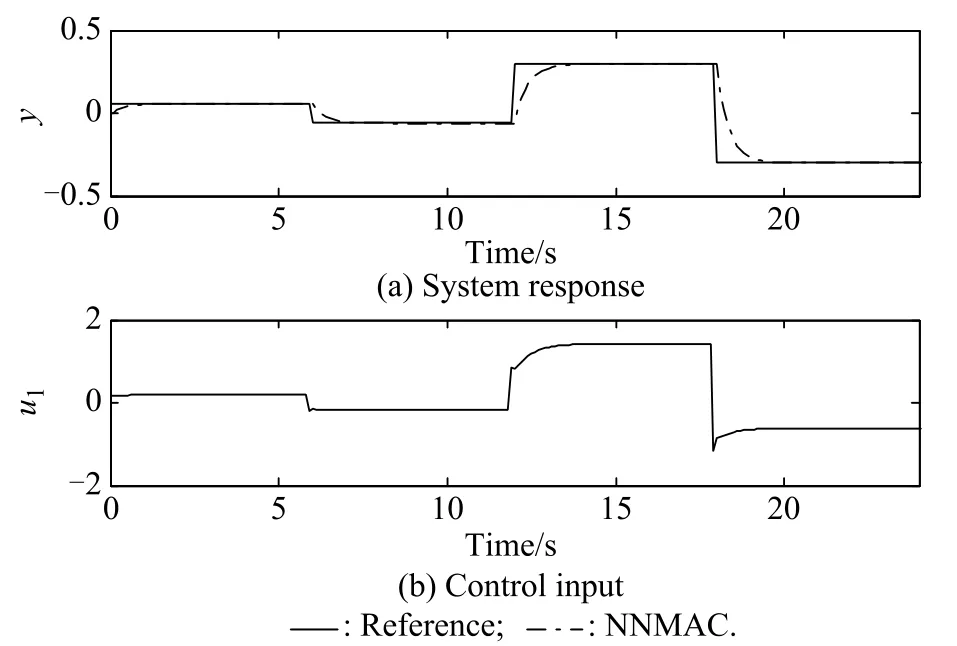
Fig.9 System response and control input using NNMAC method (D=0.1 s,α=0.7)

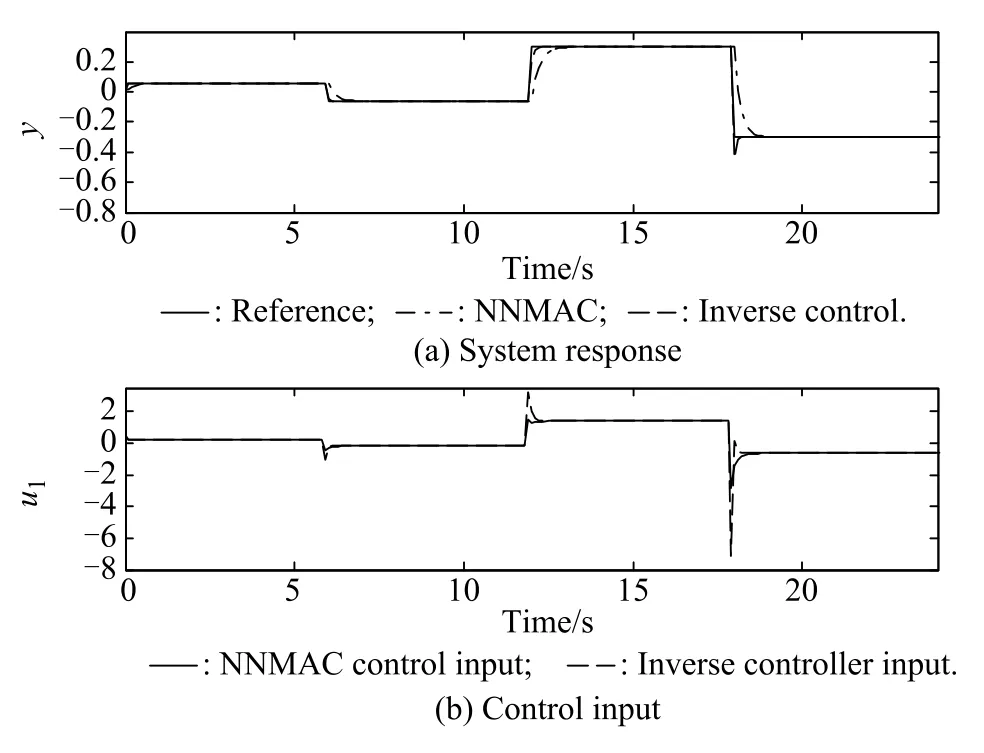
Fig.10 System response and control input using the nonlinear inverse controller and NNMAC method(D=0.1 s,α=0.5)

Finally,the parameters are set as x(0)=0.02,T= 0.1 s,D=0.12 s and α=0.5.Fig.11 shows the reference signals,the control system’s outputs,and the control inputs.

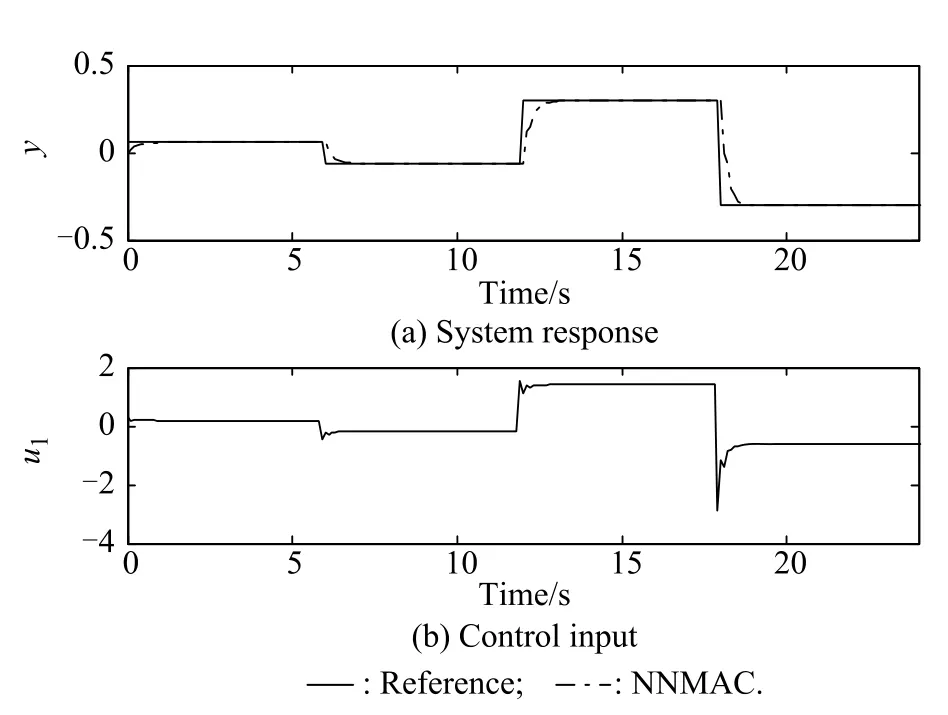
Fig.11 System response and control input using NNMAC method (D=0.12 s,α=0.5)

Example 2Consider a one-link rigid robotic manipulator[25].The dynamic equation is shown in(30).

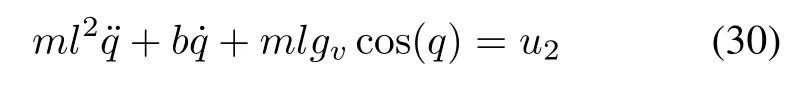
where the link is of length l and mass m,and q is the angular position with initial values q(0)=0.1 and˙q(0)=0. The parameters are chosen as m=1.2,l=1.5,gv=1 and b=1.1.The sampling period is T=0.2s and the time delay is D=0.2 s.In this example,we also use the MAC method to do the simulation.In the simulation,assume that the system is affected by the external normally distributed random disturbances with standard deviation 0.06 rad. Fig.12 shows the reference signals,the control system’s outputs,and the control inputs.The mean squared error of NNMAC and MAC control results are 0.0112 and0.0151.

Example 3Consider an inverted pendulum system [26].The dynamic equation is shown in(31).

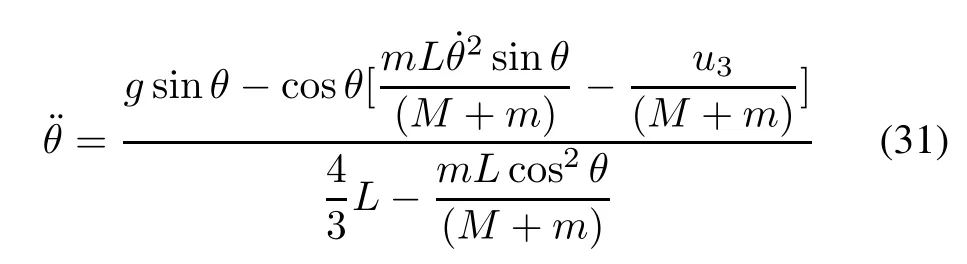
where θ is the angular displacement of the pole from the vertical,u3is the input force to the cart,g=9.8 m/s2is the acceleration due to the gravity,M=1.0 kg is the mass of the cart,m=0.5 kg is the mass of the pole,and l=0.5 m is the half length of the pole.The sampling period is T=0.2 s and the time delay is D=0.2 s.In the simulation,assume that the system is affected by the external normally distributed random disturbances with standard deviation 0.58 rad.Fig.13 shows the reference signals,the control system’s outputs,and the control inputs. The mean squared error of NNMAC and MAC control results are 0.000 7 and 0.002 7.

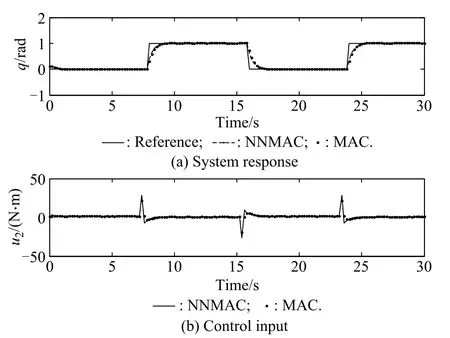
Fig.12 System response andcontrol input using NNMAC and MAC methods of Example 2

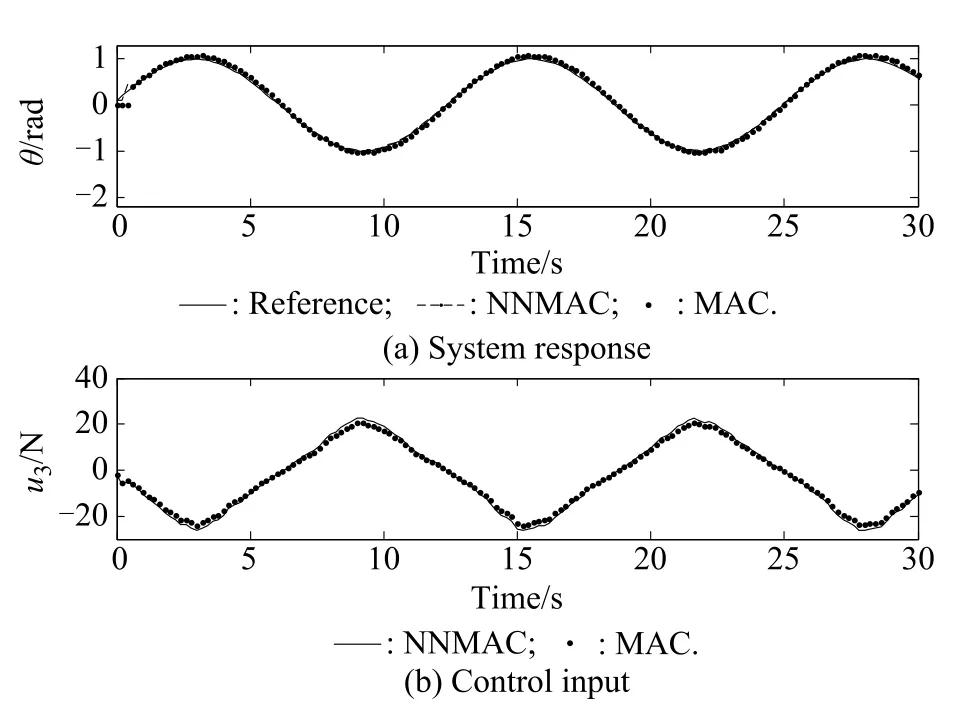
Fig.13 System response andcontrol input using NNMAC and MAC methods of Example 3

From Examples 2 and 3,it can be seen that NNMAC have better performances than MAC when the external disturbance exists.And when the system’s model is not accurate,NNMAC will provide better control results than MAC because of the good estimation ability of the neural networks.

5.Conclusions

We present the model algorithm controller using neural networks for nonlinear time delay systems.For the proposed NNMAC method two neural networks are utilized. The frst one is trained as the model of the nonlinear time delay system and the other one is trained to generate the control inputs.First,the structure of the MAC method for nonlinear systems is described.Then,the details about the two neural networks used to construct the proposed NNMAC scheme are provided.The structure and training process of the two neural networks are given in detail.The well trained neural networks are used to form the NNMAC system.The NNMAC method keeps the advantages of the MAC method and has the ability of fault tolerance due to the neural networks.The proposed control algorithm is applied to SISO nonlinear time delay systems.Computer simulations are conducted to test the performance of the proposed method and verify its effectiveness.The extension of the proposed NNMAC mothod to the MIMO nonlinear time delay systems and nonlinear systems with time varying delays is feasible.That would be the future work.

[1]Y.L.Zhang.A discretization method for nonlinear delayed non-affne systems.International Journal of Automation and Computing,2012,9(2):177–181.

[2]Z.C.Li,H.J.Gao,H.R.Karimi.Stability analysis andH∞controller synthesis of discrete-time switched systems with time delay.Systems&Control Letters,2014,66:85–93.

[3]C.E.de Souza,D.Coutinho.Robust stability and control of uncertain linear discrete-time periodic systems with timedelay.Automatica,2014,50(2):431–441.

[4]R.H.Korogui,A.R.Fioravanti,J.C.Geromel.H∞control design for time-delay linear systems:a rational transfer function based approach.European Journal of Control,2012, 18(5):425–436.

[5]Y.Zhu,Q.N.Gao,Y.Xiao.Suffcient conditions for stability of linear time-delay systems with dependent delays.Journal of Systems Engineering and Electronics,2013,24(5):845–851.

[6]H.B.Zeng,S.P.Xiao,B.Liu.Improved delay-dependent stability criteria for systems with interval delay.Journal of Systems Engineering and Electronics,2011,22(6):998–1002.

[7]X.Sun,Q.L.Zhang,C.Y.Yang,et al.Stability analysis and stabilization for discrete-time singular delay systems.Journal of Systems Engineering and Electronics,2011,22(3):482–487.

[8]B.Zhou,Z.Y.Li,Z.L.Lin.Observer based output feedback control of linear systems with input and output delays.Automatica,2013,49(7):2039–2052.

[9]J.Q.Huang,F.L.Lewis.Neural-network predictive controlfor nonlinear dynamic systems with time-delay.IEEE Trans. on Neural Networks,2003,14(2):377–389.

[10]R.Z.Song,H.G.Zhang.The fnite-horizon optimal control for a class of time-delay affne nonlinear system.Neural Computing and Applications,2013,22(2):229–235.

[11]C.W.Chen.Modeling,control,and stability analysis for timedelay TLP systems using the fuzzy Lyapunov method.Neural Computing and Applications,2011,20(4):527–534.

[12]Z.R.Xiang,R.H.Wang,Q.W.Chen.Robust reliable stabilization of stochastic switched nonlinear systems under asynchronous switching.Applied Mathematics and Computation, 2011,217(19):7725–7736.

[13]Z.R.Xiang,R.H.Wang,Q.W.Chen.Robust stabilization of uncertain stochastic switched non-linear systems under asynchronous switching.Proc.of the Institution of Mechanical Engineers–Part I:Journal of Systems and Control Engineering, 2011,225(1):8–20.

[14]Z.R.Xiang,R.H.Wang.Robust stabilization of discretetime switched non-linear systems with time delay under asynchronous switching.Transactions of the Institute of Measurement and Control,2011,33(5):591–609.

[15]Y.J.Liu,R.Wang,C.L.P.Chen.Robust adaptive fuzzy controller design for a class of uncertain nonlinear time-delay systems.International Journal of Uncertainty,Fuzziness and Knowledge-Based Systems,2011,19(2):329–360.

[16]S.C.Tong,Y.M.Li,H.G.Zhang.Adaptive neural network decentralized backstepping output-feedback control for nonlinear large-scale systems with time delays.IEEE Trans.on Neural Networks,2011,22(7):1073–1086.

[17]Y.L.Zhang,J.B.Park,K.T.Chong.Controller design for nonlinear systems with time delay using model algorithm control(MAC).Simulation Modelling Practice and Theory,2009, 17(10):1723–1733.

[18]Y.Cui,Y.J.Liu,D.J.Li.Robust adaptive NN control for a class of uncertain discrete-time nonlinear MIMO systems. Neural Computing and Applications,2013,22(3/4):747–754.

[19]W.S.Chen,L.C.Jiao,J.Li,et al.Adaptive NN backstepping output-feedback control for stochastic nonlinear strictfeedback systems with time-varying delays.IEEE Trans.on Systems,Man,and Cybernetics–Part B:Cybernetics,2010, 40(3):939–950.

[20]Y.J.Liu,S.C.Tong,D.Wang,et al.Adaptive neural output feedback controller design with reduced-order observer for a class of uncertain nonlinear SISO systems.IEEE Trans.on Neural Networks,2011,22(8):1328–1334.

[21]Z.C.Qiu,X.T.Zhang,C.D.Ye.Vibration suppression of a fexible piezoelectric beam using BP neural network controller. Acta Mechanica Solida Sinica,2012,25(4):417–428.

[22]L.Han,Z.Y.Zhang.The application of immune genetic algorithm in main steam temperature of PID control of BP network. Physics Procedia,2012,24:80–86.

[23]M.Nørgaard,O.Ravn,N.K.Poulsen,et al.Neural networks for modelling and control of dynamic systems.London: Springer Verlag,2000.

[24]N.Kazantzis,C.Kravaris.Time-discretization of nonlinear control system via Taylor method.Computers&Chemical Engineering,1999,23(6):763–784.

[25]M.Chemachema.Output feedback direct adaptive neural network control for uncertain SISO nonlinear systems using a fuzzy estimator of the control error.Neural Networks,2012, 36:25–34.

[26]M.F.Yeh.Single-input CMAC control system.Neurocomputing,2007,70(16/18):2638–2644.

Biographies

Yuanliang Zhang was born in 1979.He received his B.S.degree from Tsinghua University,China in 2001.Hereceived his M.S.and Ph.D.degrees from Chonbuk National University,South Koreain 2006 and 2009,respectively.He is currently an associate professor at the School of Mechanical Engineering,Huaihai Institute of Technology,China.His research interests include nonlinear control system and robotics.

E-mail:newlion79@gmail.com

Kil To Chong was born in 1960.He received his Ph.D.degree in mechanical engineering from Texas A&M University in 1995.Currently,he is a professor at the School of Electronics and Information Engineering at Chonbuk National University in Jeonju, South Korea,and he is the head of the Advanced Research Center of Electronics.His research interests are motor fault detection,network system control, time-delay systems,and neural networks.

E-mail:kitchong@chonbuk.ac.kr

10.1109/JSEE.2015.00019

Manuscript received October 30,2013.

*Corresponding author.

This work was supported by the Brain Korea 21 PLUS Project,National Research Foundation of Korea(NRF-2013R1A2A2A01068127; NRF-2013R1A1A2A10009458)and Jiangsu Province University Natural Science Research Project(13KJB510003).