Semi-tensor product approach to controllability and stabilizability of fnite automata
Yongyi Yan,Zengqiang Chen,and Zhongxin Liu
1.College of Computer&Control Engineering,Nankai University,Tianjin 300071,China;
2.College of Information Engineering,Henan University of Science and Technology,Luoyang 471023,China
3.College of Science,Civil Aviation University of China,Tianjin 300300,China
Semi-tensor product approach to controllability and stabilizability of fnite automata
Yongyi Yan1,2,Zengqiang Chen1,3,*,and Zhongxin Liu1
1.College of Computer&Control Engineering,Nankai University,Tianjin 300071,China;
2.College of Information Engineering,Henan University of Science and Technology,Luoyang 471023,China
3.College of Science,Civil Aviation University of China,Tianjin 300300,China
Using semi-tensor product of matrices,the controllability and stabilizability of fnite automata are investigated.By expressing the states,inputs,and outputs in vector forms,the transition and output functions are represented in matrix forms. Based on this algebraic description,a necessary and suffcient condition is proposed for checking whether a state is controllable to another one.By this condition,an algorithm is established to fnd all the control sequences of an arbitrary length.Moreover,the stabilizability of fnite automata is considered,and a necessary and suffcient condition is presented to examine whether some states can be stabilized.Finally,the study of illustrative examples verifes the correctness of the presented results/algorithms.
fnite automata,controllability,stabilizability,semitensor product of matrices,matrix approach.
1.Introduction
The theory of semi-tensor product(STP)of matrices, which was proposed by Cheng[1,2],is an important original matrix analysis method and tool.STP generalizes the conventional matrix product and preserves all the fundamental properties.Because of this,STP can theoretically replace the conventional matrix product in most engineering and science areas.STP is gaining more and more attentions and has been applied to many areas successfully,such as,Boolean networks[3–5],Boolean algebra and Boolean calculus[6],nonlinear systems[7,8],multi-agent systems [9],fuzzy control systems[10,11],adaptive control[12], graphic theory[9],and fnite automata[13].
The algebraic approach provides an elegant way for construction and analysis of fnite automata[14–16],which is very promising due to the rapid increase of computational technology[16].STP of matrices can represent the dynamics of networks in a discrete mode and can be used to analyze and control the dynamics of networks or systems. For example,[13]provides a matrix-based algebraic approach for the reachability analysis of fnite automata with the help of STP.Furthermore,the authors studied the operations of automata and bi-simulation algorithms based on the STP in[17].Another advantage of STP is the ability to prove descriptive propositions in a constructive way. Such constructive proof usually provides an algorithm for the corresponding problems[9],which can be easily done by computers.
Controllability and stabilizability analysis of fnite automata are interesting and important topics,which are necessary to lots of related problems[18–20].Dogruel et al. addressed a state equation-like method for fnite automata and defned controllability,reachability and stabilizability after the traditional framework of control theory[21].Reference[22]proposed a fx point characterization of the“controllability subset”of a deterministic Rabin automaton,by which the authors defned and analyzed the control of automata on infnite strings.The state feedback stabilization of a deterministic fnite automaton was studied in [23],and the results can be used to stabilize model predictive control(MPC)of hybrid systems.There are also some other methods to investigate the controllability and stabilizability of fnite automata[14,23].
In this paper,we investigate the controllability and stabilizability of fnite automata by using the STP of matrices, and present a new formulation to check whether a state is controllable to another one.First,the states,inputs and outputs of an automaton are expressed in vector forms.Then the STP is used to represent the transition function in the form of matrix.Using the algebraic description,we obtain a necessary and suffcient condition about controllabilityof fnite automata,by which an algorithm is established to fnd out all the control sequences.Furthermore,we present a necessary and suffcient condition of stabilizability.Using the condition,a set of states of an automaton can be examined whether they can be stabilized by a fnite control sequence.
The contributions of our work lie in that we establish a new mathematical formulation which can handle the controllability and stabilizability of fnite automata,and present some new theoretical results and algorithms by using this mathematical formulation.The advantages of the proposed method are the following.The problems of controllability and stabilizability can be represented as matrix expressions,which are different from the existing conclusions.Using the propsoed results,to check whether a state is controllable or stabilizable,we only need to calculate a sort of state transition matrix,with which we can get the conclusion easily.It is necessary to point out that the major advantages of our method are the mathematical formulation and constructive algorithms,not the reduction of computation complexity.
The remainder of the paper is organized as follows.Section 2 gives the preliminaries on the STP of matrices and some related concepts of automata.In Section 3,we investigate the controllability and stabilizability of fnite automata,and present the main results of this paper.In Section 4,we give an illustrative example to support our new results;this is followed by the conclusions in Section 5.
2.Preliminaries
This section briefy gives some necessary preliminaries on the STP and automata,which will be used throughout this paper.
Defnition 1[2] For M ∈Rm×nand N ∈Rp×q, their STP,denoted by M?N,is defned as follows:
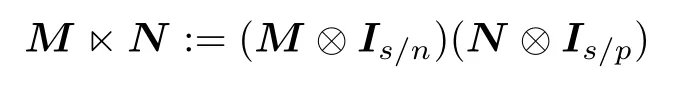
where s is the least common multiple of n and p,and⊗is the Kronecker product.
Remark 1(i)STP is a generalization of the traditional matrix product.When n=p,STP is equivalent to the latter.For matrix A,denote A1=A,Ai+1=Ai?A(i≥1).(ii)STP maintains most major properties of the conventional matrix product,among which the associativity is that for A∈Mm×n,B∈Mp×qand C∈Mr×s,then (A?B)?C=A?(B?C).
Defnition 2[2]A swap matrix W[m,n],an mn×mn matrix,is defned as follows.Its rows and columns are labeled by double index(i,j),the rows are arranged by the ordered multi-index Id[j,i;n,m],and the columns are arranged by the ordered multi-index Id[i,j;m,n].Then the element at the position[(I,J),(i,j)]is

Remark 2By Defnition 2,we know that
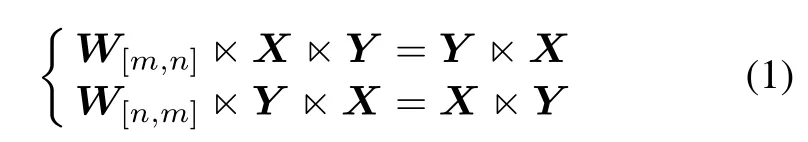
for any X∈Rmand Y∈Rn.
The following notations will be used throughout this paper.
On∈Rnis the vector with all elements being 0,while 1n∈Rnis the vector with all elements being 1.
coli(A)is the ith column of matrix A,col(A)is the set of all the columns of A.
δinis the ith column of the unit matrix In∈Rn×n, denote Δn:={δ1n,...,δnn}.
Defnition 3[24,25] An automaton is a seven-tuple A=(X,E,Y,f,g,x0,Xm),in which X,E and Y are fnite sets of states,input symbols,and outputs,respectively; x0∈X is the initial state;Xm⊂X is the set of accepted states;f and g are transition and output functions,which are defned as

where 2Xand 2Ydenote the power sets of X and Y,that is,f(x,e)⊂X,g(x,e)⊂Y.
A is called a deterministic fnite automaton(DFA)if |f(x,e)|≤1 for each x∈X and e∈E.Otherwise,A is called a nondeterministic fnite automaton(NFA).Both DFA and NFA are generally said to be a fnite automaton. Since NFAs can be converted into DFAs,this paper considers the deterministic ones only.
E∗represents the fnite string set on E,which does not include the empty transition.Given an input string e = e1···et∈ E∗,defne f(x,e) = f(f(···f(f(x,e1),e2)···),et).We call xe1→x′e2→x′′e3→···a path with respect to the given input string e and initial state x.
For a fnite automaton A=(X,E,Y,f,g,x0,Xm), where X={x1,...,xn},E={e1,...,em},Y = {y1,...,yl},identify xiwith δin(1≤i≤n),expressed as xi~δinfor simplicity,and call δinthe vector form of xi. Then X can be denoted as Δn,that is,X={δ1n,...,δnn}. Similarly,for E,identify ejwith δjm(1≤j≤m)(denoted as ej~δjm),call δjmthe vector form of ej,and use Δmto denote E,i.e.,E={δ1m,...,δmm}.We do the same things to yk(1≤k≤l),that is,identify ykwith δkl,denoted asyk~δkl,call δklthe vector form of yk,then Y can be denoted as Δl,i.e.,Y={δ1l,...,δll}.Thus,xi∈f(xj,eh) and yi∈g(xj,eh)can be expressed as δin∈f(δjn,δhm) and δil∈g(δjn,δhm),respectively.
Defnition 4[21]Controllability and stabilizability.
A state xi∈X is said to be controllable to xj∈X if for x0=xithere is an input string e=e1e2···et∈E∗, so that x(t+1)=xj,where x(t+1)is the state at time t+1,e is called a control sequence,and xie1→···et→xjis a control path.
A state xi∈X is said to be controllable if xiis controllable to any state xj∈X.
Suppose X=X1∪X2,and X1∩X2=∅.Expressed in vector forms,i.e.,Δn=Δ1n∪Δ2n,and Δ1n∩Δ2n=∅, where Δ1nand Δ2nare the vector forms of X1and X2, respectively.For example,if X={x1,x2,x3,x4,x5}, X1={x1,x3,x5},and X2={x2,x4},then Δ15= {δ15,δ35,δ55},and Δ25={δ25,δ45}.
A set of states X1⊆X is said to be controllable if for any state xj∈X2there is an xi∈X1,so that xiis controllable to xj.
A set of states X1⊆X is said to be 1-step returnable if for any state x0=xi∈X1and for any given input there exists an input ej∈E,so that f(xi,ej)=xj∈X1.
A state xj∈X is said to be reachable from xi∈X if for x0=xithere is an input string e=e1e2···et∈E∗, so that x(t+1)=xj.
A set of states X2⊆X is said to be reachable if for any state xi∈X1there is an xj∈X2,so that xjis reachable from xi.
A set of states X1⊆X is said to be stabilizable if X1is reachable and 1-step returnable.
3.Main results
In this section,we investigate the controllability and stabilizability of fnite automata by STP,and present the main results of this paper.We frst have the following result expressing the transition function as a matrix form.
Theorem 1Let F =[F1,...,Fm]be the transition structure matrix(TSM)of the fnite automaton A= (X,E,Y,f,g,x0,Xm),where X={x1,...,xn},E= {e1,...,em}.Then the input sequence e=e1e2···et∈E∗moves state xi(1≤i≤n)to state xj.
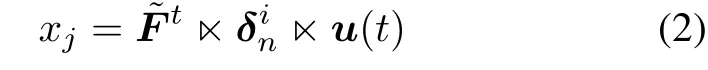
where u(t)=?tiδim=δ1m?δ2m?···?δtm,δjmis the vectorform of ej(j=1,2,...,t);δinis the vectorform of xi(i=1,2,...,n);˜F=F?W[n,m],F=[F1,...,Fm] defned as
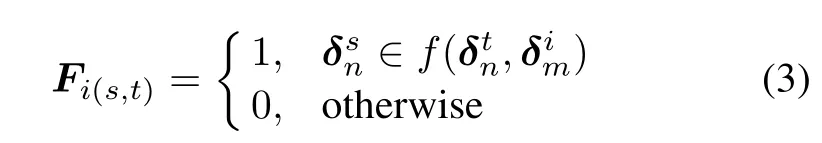
where F is called the TSM of A[21].
ProofWe frst prove that the transition function f: X×E→2Xcan be represented as f:Δn×Δm→2Δn, which is defned as

or

where˜F=F?W[n,m];δjmandδinare the vector forms of ejand xi(i=1,2,...,n;j=1,2,...,m),respectively; 2Δnis the vector form of 2X.
If A reads alphabet ejat state xiand goes to state xk(1≤k≤n),that is,f(xi,ej)=xk,by the defnition of TSM,the kth element of coli(Fj)equals to one,other elements equal to zero,i.e.,coli(Fj)=δkn.
Meanwhile,by a straightforward calculation,we know that F?δjm?δin=δkn.
Note that δknis the vector form of xk,then we have that f(xi,ej)=F?δjm?δin.
Therefore,(4)holds.Substituting(1)to(4),we then get (5).
Next,we prove(2).For the given input string e= e1e2···et,we know that
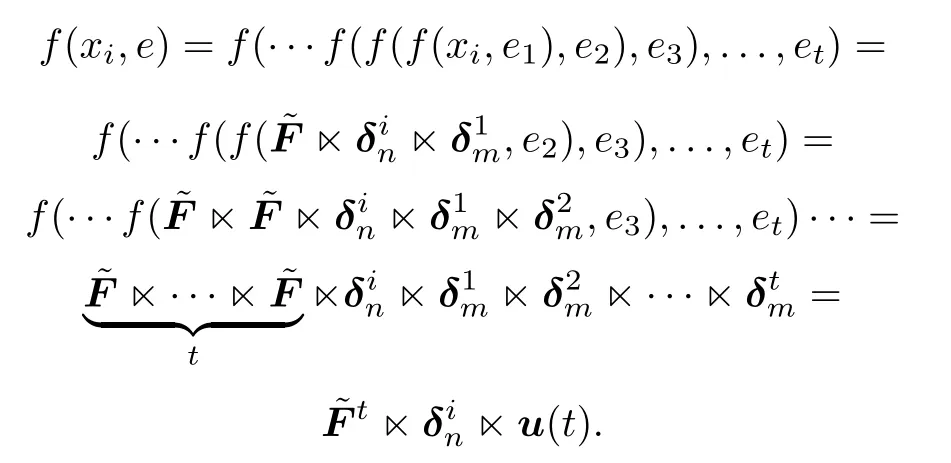
We then obtain the conclusion.
Remark 3In fact,Fiis the adjacency matrix of the eilabeled sub-graph associated with A[16];the“transition matrix”proposed in[24,26]is the transpose of Fi.
We can defne an output structure matrix(OSM)of A, denoted as G=[G1,...,Gm],as follows:

Then we have the following theorem on the output of fnite automata.
Theorem 2Assume that G=[G1,...,Gm]is the OSM of fnite automaton A,A=(X,E,Y,f,g,x0,Xm), where X={x1,...,xn},E={e1,...,em},Y = {y1,...,yl}.Then the output of A at state xi(1≤i≤n) with input e=e1e2···et∈E∗is
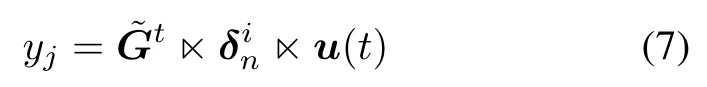
where u(t)=?tiδim=δ1m?δ2m?···?δtm,δjmis the vector form of ej(j=1,2,...,t);and δinis the vector form of xi(i=1,2,...,n);˜G=G?W[l,m].
ProofThe proof is omitted since it is very similar to that of Theorem 1. ?
Defnition 5We call the matrix˜Ft?δinin(2)the state transition matrix(STM)of A with respect to state xiand an input of length t,denoted by M(xi,t),i.e., M(xi,t)= ˜Ft?δin.
Next,we investigate the controllability conditions of fnite automata.Consider the automaton A = (X,E,Y,f,g,x0,Xm),where X={x1,...,xn},E= {e1,...,em}.Note that as described above xiis the same as δin(1≤i≤n),ejas δjm(1≤j≤m).
Theorem 3Consider the fnite automaton A with M(x0,t)being its STM.Then x0=δpnis controllable to target state x∗=δqnby an input of length t if and only if δqn∈col(M(x0,t)).
ProofNecessity.
If the initial state x0=δpncan be controlled to the target state x∗=δqnwith a string of length t,say,e=e1···et, from Theorem 1,we have

Since among the elements of u(t)only one element is 1 and the others are 0 s,we know that

That is to say,δqn∈col(M(x0,t)).We then get the necessity.
Suffciency.
By a straightforward computation,we can have
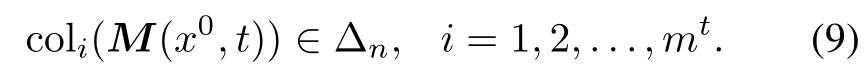
This implies that every column of M(x0,t)is that of the unit matrix In.
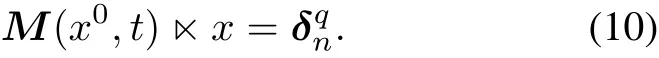
Comparing(10)with(2),we can know that e= e1e2···etis the control sequence by which x0=δpncan be controlled to x∗=δqn.By the defnition of controllability of fnite automata,x0=δpnis controllable to x∗=δqnby the input string.
Furthermore,according to[4],we can obtain the input by solving the following t-ary equation

where ei∈Δm.
From Theorem 3,Corollaries 1 and 2 follows immediately.
Corollary 1Consider the fnite automaton in Theorem 3,then n(xp,xq,t)equals the number of different paths of length t with which state x0=δpncan be controlled to x∗= δqn,where n(xp,xq,t)is the number of columns of M(x0,t)which equals to δqn.
Corollary 2For the fnite automaton A=(X,E, Y,f,g,x0,Xm)with M(x0,t)being its STM,then x0= δpnis controllable if and only if there is a positive integer t such that

Corollary 3For the fnite automaton in Corollary 2, a set of states X1⊂X is controllable if and only if there exists a positive integer t such that
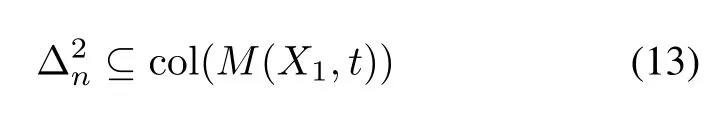
where X1∪X2=X,X1∩X2=∅;Δ2nis the vector form of X2;M(·,t)is defned as follows.
For a set of states A = {x1,x2,...,xk} ⊂ X, and a time step t,M(A,t)is a matrix whose columns are the union of the columns of the matrices M(x1,t), M(x2,t),...,M(xk,t).The following is an example.
Example 1Suppose X={x1,x2,x3,x4,x5},A= {x1,x2,x3},t=2,and

Then
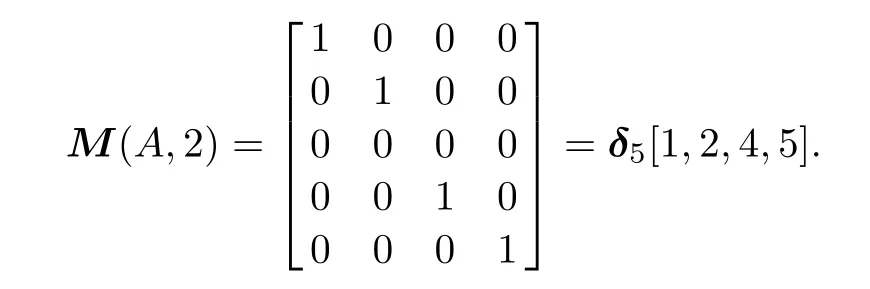
ProofFrom the defnition of M(X1,t)and Theorem 3,we know that the vector form of col(M(X1,t))is a set of states of A,and each of these states,xi,corresponds to a state in X1which can be controlled to xi.According to Defnition 4,the conclusion follows. ?
Similar to the proof of Corollary 3,we have the following conclusion on the reachability of fnite automata.
Corollary 4For the fnite automaton in Corollary 2,a set of states X1⊂X is reachable with an input string of length t if and only if

where X1∪X2=X,X1∩X2=∅;Δ1nis the vector form of X1;M(·,t)is defned as in Corollary 3.
Based on the proof of Theorem 3,we now establish an algorithm to fnd out all the control sequences of length t by which state x0=δpncan be controlled to state x∗=δqn.
Algorithm 1Given a fnite automaton A=(X,E, Y,f,g,x0,Xm),where X={x1,...,xn},E={e1,..., em},assume that its TSM is F.Identify xiand ejwith δinand δjm,respectively.To fnd all the control sequences of length t by which an initial state x0=δpncan be controlled to a target state x∗=δqn,we can take the following steps.
Step 1Compute the STM M(x0,t)= ˜Ft?δpnby Defnition 5.
Step 2Check whether δqn∈col(M(x0,t)).If not, x0=δpnis not controlled to x∗=δqn,and the computation is stopped.Otherwise,label the columns which equal to δqn,and set
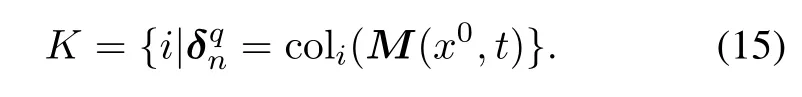
Step 3For each l∈K,considerlet
Then we have
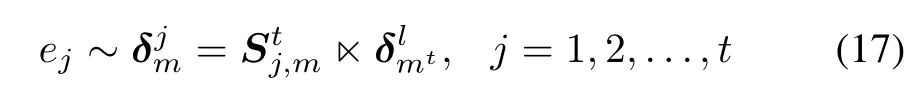
With the obtained solution(e1,e2,...,et),corresponding to l,a control sequence of length t,Pl=e1e2···etis found.
Step 4All the control sequences are{Pl|l∈K,Plis produced by Steps 1–3}.
Next, fnite automata.
Lemma 1Given a fnite automaton A=(X,E, Y,f,g,x0,Xm),where X1∪X2=X,X1∩X2=∅, E={e1,...,em}.Identify xiwith δin(1≤i≤n),and ejwith δjm(1≤j≤m),as described above.A set of states X1⊆X is 1-step returnable if and only if there is asuch that
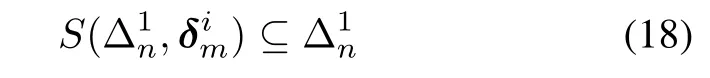
where

ProofAccording to Theorem1,we knowis a state to which the state δjncan be controlled by the inputis a set of such states.By Defnition 4,we can get the conclusion.
Theorem 4Consider the fnite automata in Lemma 1. A set of states X1⊆ X is stabilizability with an input string of length t if and only if there exists asuch that

ProofSince X1is stabilizable if and only if X1is reachable and 1-step returnable,the proof follows from Lemma 1 and Corollary 4.
4.Illustrative examples
This section gives an example to verify the correctness of the results/algorithms obtained in this paper.The example is a fnite automaton[27]which accepts the language {ω|ω∈{1,2,3}+,ω is evenly divisible by four}.
Example 2Consider the fnite automaton A=(X, E,Y,f,g,x0,Xm)shown in Fig.1,where X={x1,x2, x3,x4,x5},E={1,2,3},x0=x1,Xm={x5}.
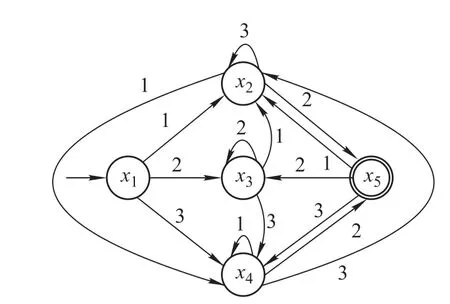
Fig.1 Finite automaton model of example 2
The TSM of A is
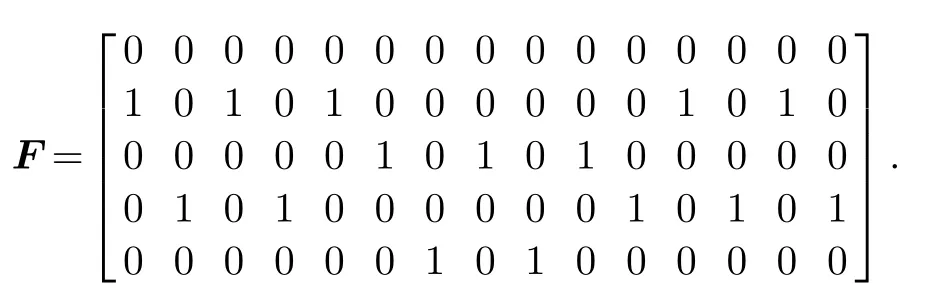
The case of t=1 is trivial,we consider the following cases.
When t=2,the STM M(x1,2)can be obtained by Theorem 1 or Defnition 5 as

By Theorem 3,we know that state x0=δ15can be controlled to states δ25,δ35,δ45and δ55by a control string of length2,among which,according to Corollary1,the states δ25and δ45can be reached three times,state δ55twice,and state δ35once.
Suppose δ55is the target state,according to Step 2 of Algorithm 1,then K={2,8}.
we have

That is e1=1,e2=2.Therefore,the control sequence is e=12,and the control path from x1to x5is x1
1→x2
2→x5.
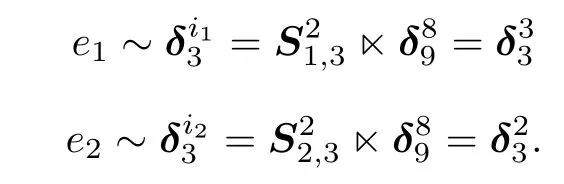
That is e1=3,e2=2,the control sequence is e=32, and the corresponding control path is x13→x4
2→x5.
Since x5∈Xm,the language of length 2 accepted by A is

Thus,by Theorem 3,the initial state x1can be controlled to states δ25,δ35,δ45and δ55by a control sequence of length 3,among which,according to Corollary 1,the states δ25and δ45can be reached 9 times,δ556 times, δ353 times.Suppose δ55is the target state,then K = {2,8,11,17,20,26}(see Step 2 of Algorithm 1).
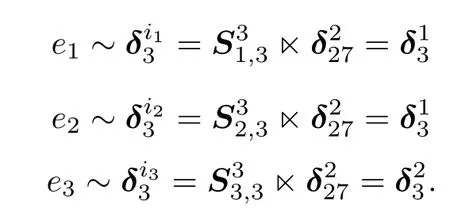
Therefore,e1=1,e2=1,e3=2,the control sequence is e=112,and the control path is x11→x2
1→x4
2→x5.
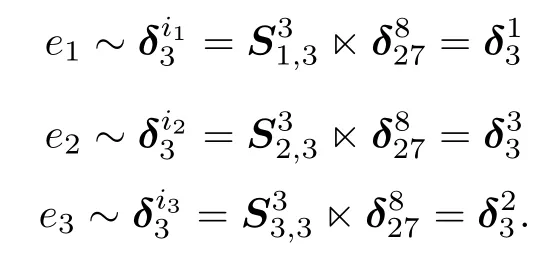
Therefore,the control sequence of length 3 is e=132, the control path is
Similarly,for l s taking the following values,the control sequences and paths are as follows.
l=11,the control sequence is e=212,and the path is
l=17,the control sequence is e=232,and the path is
l=20,the control sequence is e=312,and the path is
l=26,the control sequence is e=332,and the path is
Thus,we can get that the language of length 3 accepted by A are
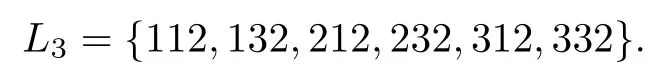
When t=4,the STM M(x1,4)is
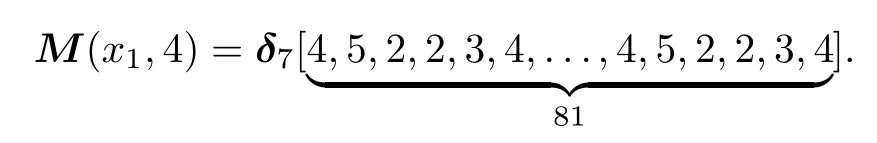
Setting δ55as the target state,using Algorithm 1,we can get that the language of length 4 accepted by A are

Using the same method,we can also fnd out control sequences by which other states,not the initial state,can be controlled to a target state,and languages of an arbitrary length can be accepted by A.
5.Conclusions
STP is a very effective tool to model the dynamics of a discrete system.In this paper,we frst use the STP to convert the transition function of fnite automata into an algebraic expression.Then,using this algebraic description, we obtain a necessary and suffcient condition for checking the controllability of a set of states.According to the proposed algorithm,to check/determine whether a set of states is controllable/stabilizable,one only needs to compute a kind of STM,with which the conclusioncan be easily obtained.The condition suggests an algorithm to fnd out all the control sequences by which one state can be controlled to another one.Moreover,the stabilizability of fnite automata is considered.We present a necessary and suffcient condition to check whether a set of states can be stabilized.As[13]pointed out that the matrix framework provides an effective way in the analysis and computation for fnite automata.Many interesting related problems such as task assignment and hierarchical decomposition can be studied by STP.
[1]D.Z.Cheng.Semi-tensor product of matrices and its application to Morgen’s problem.Science in China Series F:Information Sciences,2001,44(3):195–212.
[2]D.Z.Cheng,H.S.Qi,Y.Zhao.An introduction to semi-tensor product of matrices and its applications.Singapore:World Scientifc Publishing,2012.
[3]D.Z.Cheng.Disturbance decoupling of Boolean control networks.IEEE Trans.on Automatic Control,2011,56(1):2–10.
[4]D.Z.Cheng,H.S.Qi,Y.Zhao.Analysis and control of Boolean networks:a semi-tensor product approach.Acta Automatica Sinica,2011,37(5):529–540.
[5]F.F.Li,J.T.Sun.Controllability and optimal control of a temporal Boolean network.Neural Networks,2012,34(6):10–17.
[6]H.T.Li,Y.Z.Wang.Boolean derivative calculation with application to fault detection of combinational circuits via the semi-tensor product method.Automatica,2012,48(4):688–693.
[7]Z.Q.Li,Y.Qiao,H.S.Qi,et al.Stability of switched polynomial systems.Journal of Systems Science and Complexity, 2008,21(3):362–377.
[8]D.Z.Cheng,H.S.Qi.Non-regular feedback linearization of nonlinear systems via a normal form algorithm.Automatica, 2004(40):439–447.
[9]Y.Z.Wang,C.H.Zhang,Z.B.Liu.A matrix approach to graph maximum stable set and coloring problems with application to multi-agent systems.Automatica,2012,48(7):1227–1236.
[10]D.Z.Cheng,H.S.Qi.Matrix expression of logic and fuzzy control.Proc.of the 44th IEEE Conference on Decision and Control,and the European Control Conference,2005:3273–3278.
[11]Y.Y.Yan,Z.Q.Cheng,Z.X.Liu.Solving type-2 fuzzy relation equations via semi-tensor product of matrices.Control Theory and Technology,2014,12(2):173–186.
[12]X.X.Zhang.Semitensor product based adaptive control for attitude tracking of spacecraft with unknown external disturbances.Journal of Control Theory and Applications,2012, 10(3):292–296.
[13]X.R.Xu,Y.G.Hong.Matrixexpression and reachability analysis of fnite automata.Journal of Control Theory and Applications,2012,10(2):210–215.
[14]L.Cienciala,L.Ciencialova.Membrane automata with priorities.Journal of Computer Science and Technology,2004, 19(1):89–97.
[15]Y.Gang.Decomposing a kind of weakly invertible fnite automata with delay 2.Journal of Computer Science and Technology,2003,18(3):354–360.
[16]K.H.Kim.Boolean matrix theory and applications.New York:Dekker,1982.
[17]X.R.Xu,Y.G.Hong,H.Lin.Matrix approach to simulation and bisimulation analysis of fnite automata.Proc.of the 10th World Congress on Intelligent Control and Automation,2012: 2716–2721.
[18]S.Abdelwahed,W.Wonham.Blocking detection in discrete event systems.Proc.of the American Control Conference, 2003:1673–1678.
[19]J.Lygeros,C.Tomlin,S.Sastry.Controllers for reachability specifcations for hybrid systems.Automatica,1999,35(3): 349–370.
[20]A.Casagrande,A.Balluchi,L.Benvenuti,et al.Improving reachability analysis of hybrid automata for engine control. Proc.of the 43rd IEEE Conference on Decision and Control, 2004:2322–2327.
[21]M.Dogruel,U.Ozguner.Controllability,reachability,stabilizability and state reduction in automata.Proc.of the IEEE Conference on Intelligent Control,1992:192–197.
[22]J.G.Thistle,W.M.Wonham.Control of infnite behavior of fnite automata.SIAM Journal on Control and Optimization, 1994,32(4):1075–1097.
[23]K.Kobayashi,J.I.Imura,K.Hiraishi.Stabilization of fnite automata with application to hybrid systems control.Discrete Event Dynamic Systems:Theory and Applications,2011, 21(4):519–545.
[24]S.Eilenberg.Automata,languages,and machines,New York: Academic Press,1974.
[25]C.G.Cassandras,S.Lafortune.Introduction to discrete event systems.New York:Springer,1999.
[26]S.Seshu,R.Miller,G.Metze.Transition matrices of sequential machines.IRE Trans.on Circuit Theory,1959,6(1):5–12.
[27]W.Y.Chen.Theory of fnite automata.Chengdu:University of Electronic Scinece Technoldge Press,2007.(in Chinese)
Biographies

Yongyi Yan was born in 1980.He received his B.S.and M.S.degrees in mathematics from Luoyang Normal University,Xidian University,in 2005 and 2008,respectively,and is currently pursuing his Ph.D.degree in control theory and engineering at Nankai University,Tianjin,China.His current research interests are in the felds of modeling and optimization of complex systems,fuzzy control,and intelligent predictive control.
E-mail:yyyan@mail.nankai.edu.cn

Zengqiang Chen was born in 1964.He received his B.S.,M.E.and Ph.D.degrees from Nankai University,in1987,1990,and1997,respectively.Heiscurrently a professor of control theory and engineering of Nankai University,and deputy director of Institute of Robotics and Information Automation.His current research interests include intelligent predictive control,chaotic systems and complex dynamic network,and multi-agent system control.
E-mail:chenzq@nankai.edu.cn

Zhongxin Liu received his B.E.and Ph.D.degrees in Nankai University,in 1997 and 2002,respectively.He is currently a professor of control theory and engineering of Nankai University,Tianjin, China.His current research interests include multiagent systems,complex and dynamic networks,and computer control and management.
E-mail:lzhx@nankai.edu.cn
10.1109/JSEE.2015.00018
Manuscript received September 13,2013.
*Corresponding author.
This work was supported by the National Natural Science Foundation of China(61174094)and the Tianjin Natural Science Foundation of China(13JCYBJC17400;14JCYBJC18700).
 Journal of Systems Engineering and Electronics2015年1期
Journal of Systems Engineering and Electronics2015年1期
- Journal of Systems Engineering and Electronics的其它文章
- Dynamic channel reservation scheme based on priorities in LEO satellite systems
- Adaptive beamforming and phase bias compensation for GNSS receiver
- Novel dual-band antenna for multi-mode GNSS applications
- Nonparametric TOA estimators for low-resolution IR-UWB digital receiver
- Effcient hybrid method for time reversal superresolution imaging
- Adaptive detection in the presence of signal mismatch
