Observability analysis of feature aided terminal guidance systems
Shijie Fan,Hongqi Fan,Huaitie Xiao,*,Jianpeng Fan,and Qiang Fu
1.National Key Laboratory of Automatic Target Recognition,National University of Defense Technology,Changsha 410073,China;
2.College of Electronic Science and Engineering,National University of Defense Technology,Changsha 410073,China
Observability analysis of feature aided terminal guidance systems
Shijie Fan1,Hongqi Fan1,Huaitie Xiao1,*,Jianpeng Fan2,and Qiang Fu1
1.National Key Laboratory of Automatic Target Recognition,National University of Defense Technology,Changsha 410073,China;
2.College of Electronic Science and Engineering,National University of Defense Technology,Changsha 410073,China
Feature aided design of estimators and guidance laws can signifcantly improve the interception performance of the terminal guidance system.The achieved enhancement can be effectively assessed by observability analysis methods.This paper frst analyzes and discusses the existing assessment methods in a typical endgame scenario with target orientation observations.To get over their defciencies,a novel singular value decomposition (SVD)method is proposed.Employing both theoretical analysis and numerical simulation,the proposed method can represent the degree of state observability which is enhanced by integrating target features more completely and quantitatively.
terminal guidance,feature aided,observability,singular value,orientation observation.
1.Introduction
With the development of aviation weapons,the maneuverability of the new aircraft is surprisingly improved,e.g.,the unmanned aircraft and the supersonic cruise missile[1,2]. Compared with the traditional targets,these new ones are more threatening for the missile defense system.Successful interception of such targets requires a very short miss distance or even a direct hit[1–5].In the last decade,the feature aided or feature integrated design of estimators and guidance laws signifcantly reduces the estimation delay of the target acceleration using the relationship between optical or radar signatures and target motion modes[6–10]. That makes a great improvement of the interception performance.
For the radar seeker,two maneuver detectors combined with the variable structure multimode estimators are proposed employing the amplitude-fuctuating feature of radar echo[7]and the one-dimension inverse synthetic aperture radar(ISAR)image distortion feature,respectively[8,9]. Their methods greatly reduce the maneuver detection delay and the miss distance.For the optical seeker,Oshman et al.[6,10]used the image changing caused by different target attitudes to reduce the target reachable set which improves the estimation of the zero-effort miss(ZEM)distance.Consequently,the missile guidance accuracy is signifcantly improved.
A qualitative conclusion can be drawn from the aforementioned researches:feature aided or feature integrated design of estimators and guidance laws is benefcial to the interception performance improvement,due to the increased information of target motion brought by integrating features.However,few studies focus on discussion of the performance enhancement achieved by integrating the target features,independent of any particular estimators or guidance laws.
Oshman made the frst attempt by an observability analysis method[6].The smallest singular value of the observability matrix is utilized to quantify the system observability variation after integrating the target features.It is demonstrated that if the smallest singular value is increased after integrating the target orientation observations,then the observability is enhanced.Note that the observability analysis method is independent of any estimator or guidance law parameter.It is suitable to analyze the effect of the target features on the interception performance theoretically.But under some conditions,the smallest singular value only provides a yes-or-no type answer to the system observability to some extent.That means it only indicates the system is absolute observableor absolute unobservable and cannot scale the degrees of observability.Moreover, the smallest singular value fails to distinguish which state observability is enhanced by integrating the target features.
This paper introduces a more comprehensive observability analysis method:the singular value decomposition (SVD)method which qualifes for the explanation of theinterception performance improvement achieved by integrating the target features.The remainder of this paper is organized as follows.In the next section,a mathematical model of the feature aided terminal guidance system and the basic defnition of observability analysis are briefy introduced.A rationality analysis of the observability analysis method based on the smallest singular value and its defciencies are presented in Section 3.In Section 4,the basic principle and application discussion of the proposed method are described in detail.Concluding remarks are offered in the fnal section.
2.Problem formulation
2.1Mathematical model
A typical two-dimensional geometry of the endgame scenario in the initial light-of-sight(LOS)coordinate system is shown in Fig.1[6].

Assume that both of the target and the missile dynamics are expressed by frst-order transfer functions with time constants τTand τM,respectively,and then the nonlinear kinematics and dynamics equations can be written as

where R is the distance between the target and the missile; λ is the LOS angle;γM,aM,VMand γT,aT,VTare the missile and target path angles,accelerations(perpendicular to the respective velocities),and speeds,respectively.and acTare the missile and target acceleration commands, respectively.
To facilitate the application of the following observability analysis,some simplifcations are used,enabling to perform the analysis using analytical expressions.Thus, VM,aMand γM(all directly measurable variables)are assumed known.Moreover,the target acceleration dynamics is assumed ideal(i.e.,aT=acT).Then we obtain the following state vector:
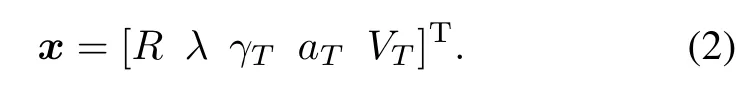
Assuming acTis a constant,the corresponding state equations can be derived from(1):
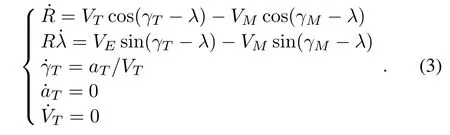
Then we consider the system measurement equations with target features aided and without target features aided. Taking an infrared(IR)seeker as an example,the classical proportion navigation(PN)guidance law is usually used [11].The corresponding measurement equation is

which is defned as the measurement equation without target features aided herein.When the target takes a hard evasive maneuver,the interception performance is fairly poor as only the LOS angle can be measured[4,7].
In fact,as we know,for the target controlled by the pure aerodynamic force or the hybrid controlled by the aerodynamic and direct force[12],the rotation around centroid will be activated when maneuvering occurs.For example,the missile taking a bank-to-turn(BTT)maneuver will make the bank angle change.The principle of the horizontal coordinate turn for a BTT missile is illustrated in Fig.2.From Fig.2 we know that,the bank angle φ is related to the target acceleration via the equation

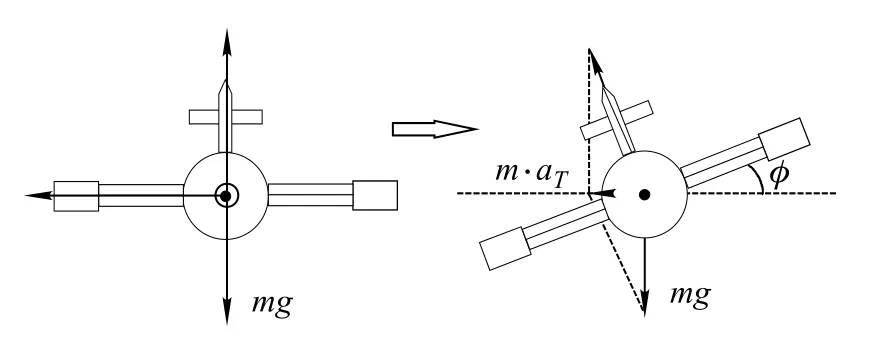
Fig.2 Principle of horizontal coordinate turn for BTT missile
Providen φ can be measured by the IR seeker(such as computer vision techniques[13]),the target optical features will offer the information of the maneuver(direction and intensity).It is signifcant for both the estimatorand the guidance law design[7–10].Assuming the measurement integrates the target orientation observations,the measurement equation with target features aided is

2.2Basic defnition of observability analysis
According to the defnition of the system observability [14],the initial system state x0can be determined uniquely by measurement sequence z if and only if the observability matrix O is nonsingular.That is
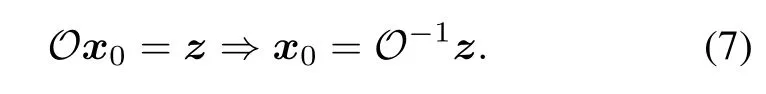
For the linear time-invariant system,the well-known observable condition is the Kalman observable condition or the P-B-H observable condition[14].For the nonlinear system


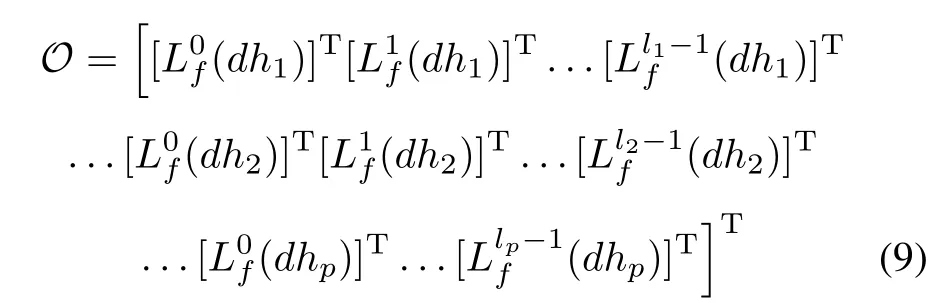
is nonsingular[15].
In(9),dhidenotes the gradient of the ith component of h with respect to x.L1f(dhi)is the Lie derivative of dhiwith respect to f.{li}p1is also called the observable index.The detailed defnitions and derivations can be found in[15].
Therefore,the observability matrices corresponding to (4)and(6),respectively,are

It is noted that the observable indexes lλand lφin satisfy

and lφ=1,lλ=4 in this scenario.
The singularity of the observability matrix O just provides a yes-or-no type answer to the system observability.That means the system is absolute observable or absolute unobservable.It cannot scale the degrees of the system observability.In the research on the inertial navigation system[16,17]and the bearing-only tracking system[18–20],the singular values,eigenvalues and eigenvectors,condition number of O are widely used to analyze the degrees of the system observability.The method proposed by Oshman is based on the smallest singular value of O.In the next section,the rationality analysis of this method used in the aforementioned system is presented.It is demonstrated that the smallest singular value of O is not suitable to indicate the performance enhancement achieved by integrating the target features as well.
3.Rationality analysis of the smallest singular value based method
3.1Basic principle
According to the perturbation theory[21],if z is perturbed by k,the perturbation h of x0in(1)is
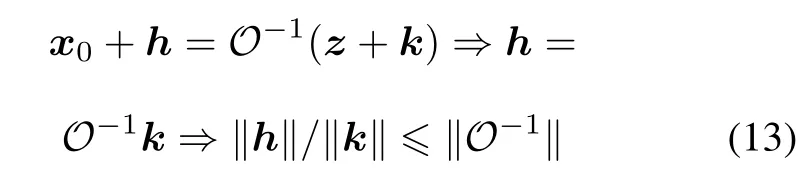
and the relative error

So?O??O−1?can be regarded as the condition number for this problem.If the condition number is large,the estimation of x0is easily perturbed by k.Given the spectral norm of O,we get

where δmaxand δminare the largest and the smallest singular values of O,respectively.Thus,the larger the δminor the smaller the k,the higher the degree of observability.
3.2Rationality analysis
Following[6],an open-loop(no guidance)simulation study is carried out to assess the degree of observability enhancement achieved by integrating the target features. For this purpose,a head-on interception scenario is chosen, where the target performs a bang-bang maneuver at tsw[22].The missile performs no controlled maneuver,fying nearly at its original heading and maintaining seeker lock on the target.The missile and target paths are shown in Fig.3,in which tfis the fight time.

Fig.3 Trajectories of missile and target in open-loop numerical study
Assume both the missile speed¯VMand the target speed ¯VTare constant.The simulation parameters are summarized in Table 1,where γM0and γT0are the path angles at the beginning of the endgame.
Fig.4 shows time histories of the smallest singular values of both observability matrices with the target maximum acceleration aTmaxequal to 5g.Throughout the scenario both observability matrices maintain full rank;however,the effect of the orientation observation on the system’s observability is quite substantial,as the smallest singular value is increased by more than two orders of magnitudes.The similar results can also be obtained by the condition numbers of both observability matrices in Fig.5.
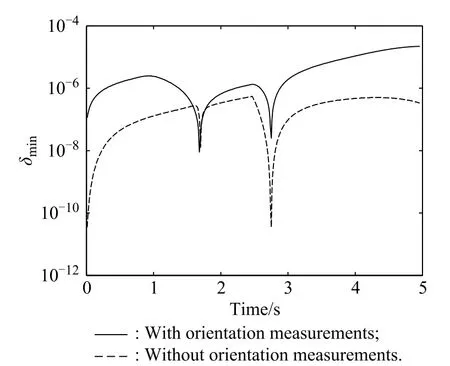
Fig.4 Smallest singular values of observability matrices(aTmax=5g)
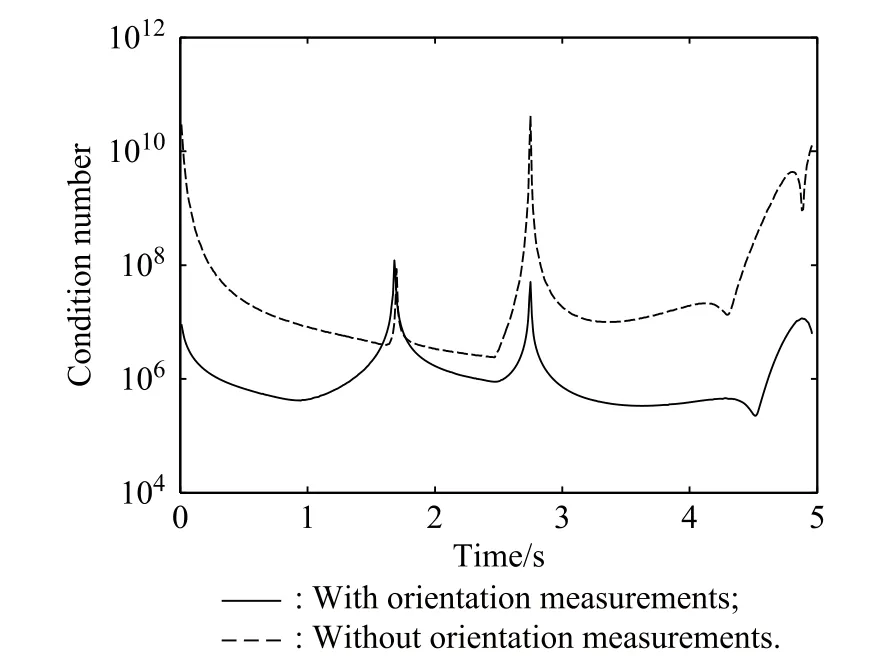
Fig.5 Condition numbers of observability matrices(aTmax= 5g)
It is noted that the analysis results are independent of any particular estimator and guidance law and thus give an excellent indication on the performance enhancement that can be expected from any estimator that judiciously exploits the information contained in the new target maneuver observations.This is an advantage of the observability analysis method indeed.But the smallest singular value of the observability matrix is not enough to quantify the observability to some extent due to the following reasons:
Remark1If δmin→0,the smallest singular value also provides a yes-or-no type answer to the system overall observability like the singularity of the observability matrix. It cannot represent the degree of system observability completely.Using δminto quantify the observability enhancement is meaningless,which is depicted in Fig.4.
Besides,δminis more sensitive to the relative geometry of missile-to-target than the new orientation measurement.Fig.6 compares the time histories of the smallest singular values of both observability matrices with different maximum accelerations.Superimposed on this fgure is the smallest singular value when the target maximum acceleration is equal to 5g without orientation measurements, added for reference.A different conclusion that the new target maneuver observations do not enhance the degree of observability could be drawn.Similar results can also be obtained in the closed-loop scenario when the missile adopts different guidance laws,such as PN versus differential game-based guidance law(DGL/1).
Remark 2δmintells one nothing about which state observability is enhanced by the new orientation measurement.
To explain the second reason,an SVD method is proposed in the next section.This method is more suitable to indicate the performance enhancement achieved by integrating the target features.
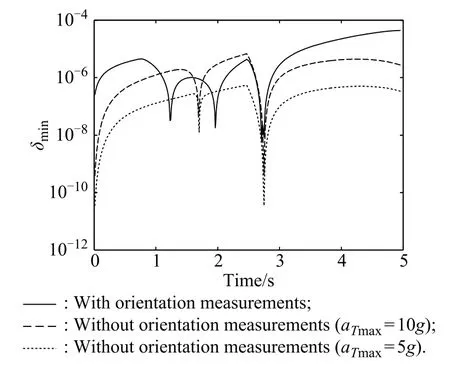
Fig.6 Smallest singular value of the observability matrix
4.SVD method
4.1Basic principle
Take an SVD of the observability matrix O,that is

where U and V are two unitary matrices
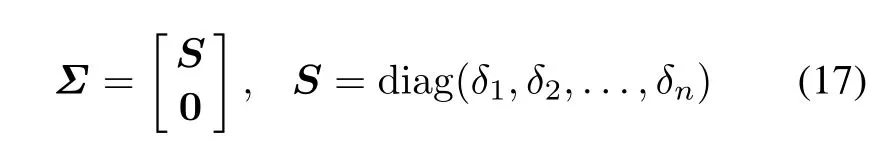
where δ1≥δ2≥···≥δn>0,and δiis the singular value of O.Left multiply OTin both sides of(7),we get
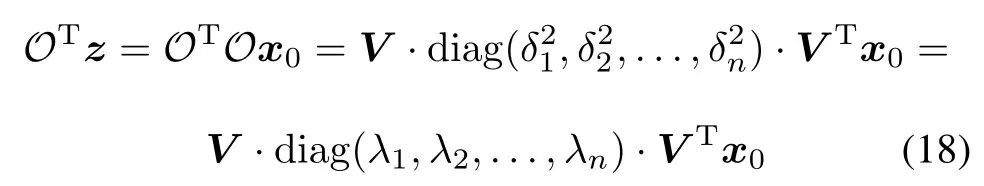
where λiare the eigenvalues of O.Then both sides of(7) are left multiplied by VT
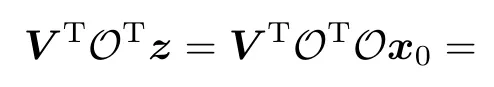
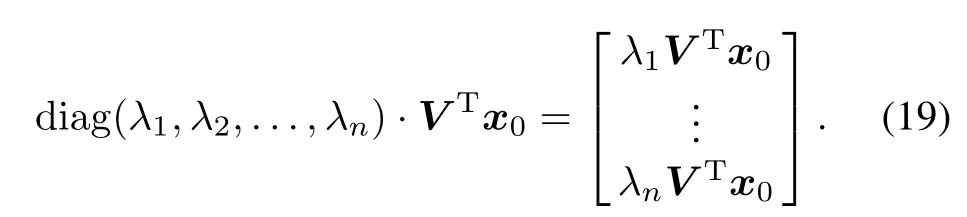
Obviously,the eigenvalue is equivalent in analysis of the system observability to the singular values.According to (19),three different situations depending on the eigenvalue can be summarized to qualify the degree of observability:
(i)If λi=0,the corresponding states combination vix0(viis the column vector of V)is unobservable completely;
(ii)If λi→ 0,the corresponding states combination vix0is less observable;
(iii)If λi/=0,the observability of vix0is also determined by the highest order of the measurement derivative in(VTOTz)iwhich is the ith component of VTOTz.It means that the higher the order of the measurement derivative is,the slower the estimation of vix0is and the more seriously the estimation is perturbed by measurement.
In this way,the proposed method tells us not only which state or states combination observability are enhanced, but also how the measurement perturbation infuences the states estimation.Therefore,we can explain the second reason in the previous subsection.
4.2Discussion
We still take the open-loop scenario when aTmax=10g as an example and the numerical analysis method is also used.Table 2 and Table 3 show the eigenvalues and the corresponding states combination in these two different situations when t=2.5 s.Although the eigenvalue values vary the whole interception,the corresponding states combinations are fxed more or less with variation of coeffcients. Hence,we just show the result when t=2.5 s for simplicity.

Table 2 States combination corresponding to each eigenvalue without orientation measurement
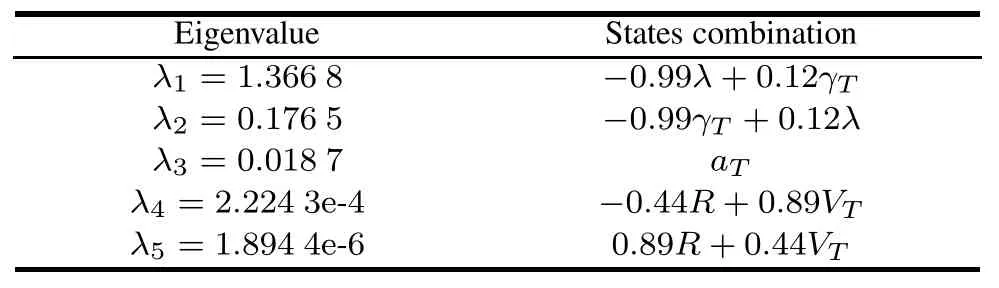
Table 3 States combination corresponding to each eigenvalue with orientation measurement
It is noted that the smallest eigenvalue λ5→ 0 means the corresponding states combination is barely observable in both situations,and thus is meaningless to quantify the degree of observability to some extent.On the other hand, the states combination corresponding to the smallest eigenvalue is range R and target velocity VT.Regardless of the constant VT,the smallest eigenvalue(or the smallest singular value)just indicates the observability of R in this scenario.In fact,the observability analysis of bearing-only tracking applications[18,19]demonstrates that the observability of R has a closer relationship with the relative geometry of missile-to-target than aT.That is the reason why δminis more sensitive to the relative geometry of missileto-target than the new orientation measurement.Hence, the smallest eigenvalue cannot represent the observability enhancement by the new orientation measurement suffciently.
We chose the eigenvalue whose states combination includes aTwith the largest coeffcient as the observability enhancement indication,denoted as λ(aT),based on the following two assumptions:
Assumption 1The measurement derivative order of each state is equal.
Assumption 2The magnitude orders of R,aTand VTare equal which are much larger than the magnitude orders of λ and γT.
Although it is demonstrated that VTOTis full rank by the numerical analysis which means the highest orders of the measurement derivative in(VTOTz)iare fve and four in these two situations,respectively.Assumption 1 is still adopted to simplify the analysis.Assumption 2 is tenable obviously.It makes sense that if one eigenvalue corresponds to the states combination,it primarily represents the states whose coeffcients and magnitude orders are much larger than others.For example,λ4in Table 2, represents aTand VTprimarily.
Fig.7 shows time histories of λ(aT)in these two different situations.We can see that the effect of the orientation observation on the system’s observability is quite substantial during the whole interception.Furthermore,at the beginning and the bang-bang instant(tsw)when the target acceleration switches,the beneft of using the bank-angle measurement is conspicuous.It also illuminates that a constant acceleration maneuver does not,usually,pose a real challenge to the missile guidance system.For the target acceleration estimator,the more diffcult problem is to detect timely a maneuver direction switch.This conclusion is coincident with[6]in which it can be explained by the sensitivity derivative of(5)
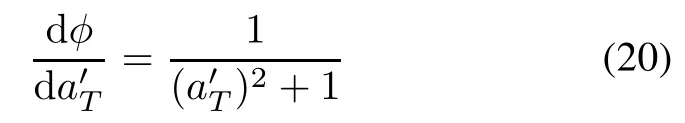

Fig.7 Eigenvalue corresponding to aT(aTmax=10g)
Obviously,λ(aT)is a better choice to assess the performance enhancement of the feature aided terminal guidance system in this scenario.To sum up,the state observability enhancement achieved by integrating target features should be scaled by a comprehensive analysis about the corresponding eigenvalue of the observability matrix,the highest order of the measurement derivative and the states magnitude orders.
5.Conclusions
Observability analysis is an effective method to assess the performance enhancement for the feature aided terminal guidance system.Compared with the smallest singular value method,the proposed SVD method clearly shows which state or states combination observability is enhanced by integrating target features.To some extent, it also presents the infuences of measurement errors and the states magnitude orders on the states observability.The proposed method is validated via a typical endgame scenario.It is demonstrated that the new target orientation observation can effectively improve the target acceleration observability.
It should be emphasized that the analysis method proposed in this paper is applied to two/three dimensional,linear/nonlinear,and radar/IR scenarios.In fact,it also can be utilized to analyze the beneft brought by other states or observations(not related to feature)to improve the interception performance.In the newest literature[23],a guidance law is designed to generate an oscillatory trajectory perpendicular to the collision course to enhance the observability during the beginning of the homing phase.Therefore,the observability analysis method provides the theoretical base for the design of the estimator and the guidance law in the terminal guidance system,especially for the feature aided design methodology.
[1]J.Shinar,T.Vladimir.What happens when certainty equivalence is not valid?:Is there an optimal estimator for terminal guidance.Annual Reviews in Control,2003,27(2):119–130.
[2]Y.H.Kim,C.K.Ryoo,M.J.Tahk.Guidance synthesis for evasive maneuver of anti-ship missiles against close-in weapon systems.IEEE Trans.on Aerospace and Electronic Systems, 2010,46(3):1376–1388.
[3]J.Shinar,T.Shima.A game theoretical interceptor guidance law for ballistic missile defense.Proc.of the 35th Conference on Decision and Control,1996:2780–2785.
[4]J.Shinar,T.Shima.Nonorthodox guidance law development approach for intercepting maneuvering targets.AIAA Journal of Guidance,Control,and Dynamics,2002,25(4):658–666.
[5]J.Shinar,Y.Oshman.Optimal integration of estimation and guidance for interceptors.Haifa,Israel:Israel Institute of Technology,2005.
[6]Y.Oshman,D.Arad.Enhanced air-to-air missile tracking us-ing target orientation observations.AIAA Journal of Guidance, Control,and Dynamics,2004,27(4):595–606.
[7]H.Q.Fan.Technology on maneuvering target motion mode identifcation in active homing guidance.Changsha,China: National University of Defense Technology,2008.
[8]Y.L.Zhu,H.Q.Fan,Q.Fu.Target turning maneuver detection using high resolution doppler profle.IEEE Trans.on Aerospace and Electronic Systems,2012,48(1):762–779.
[9]Y.L.Zhu,H.Q.Fan,Z.Q.Lu.A novel maneuver detector based on back propagation neural network.Signal Processing, 2011,91(4):1054–1059.
[10]Y.Oshman,D.Arad.Differential game based guidance law using target orientation observations.IEEE Trans.on Aerospace and Electronic Systems,2006,46(1):316–326.
[11]N.Dhananjay,D.Ghose.Accurate time-to-go estimation for proportional navigation guidance.AIAA Journal of Guidance, Control,and Dynamics,2014,37(4):1378–1383.
[12]H.Yan,H.Ji.Integrated guidance and control for dualcontrol missiles based on small-gain theorem.Automatica, 2012,48(10):2686–2692.
[13]R.L,L.Zhang,Y.Sun,et al.A review of recent advances in registration techniques applied to minimally invasive therapy. IEEE Trans.on Multimedia,2013,15(15):983–1000.
[14]C.T.Chen.Introduction of linear system theory.New York: Holt,Rinehart and Winston,1970.
[15]R.Marino,P.Tomei.Nonlinear control design.Roma:Pearson Education Limited,1996.
[16]P.Huxel,R.Bishop.Navigations algorithms and observability analysis for formation fying missions.AIAA Journal of Guidance,Control,and Dynamics,2009,32(4):1218–1231.
[17]F.Ham,R.Brown.Observability,eigenvalues,and kalman fltering.IEEE Trans.on Aerospace and Electronic Systems, 1983,16(2):269–273.
[18]S.C.Nardone,V.J.Aidala.Observability criteria for bearingsonly target motion analysis.IEEE Trans.on Aerospace and Electronic Systems,1981,17(2):162–166.
[19]S.A.R.Hepner,H.P.Geering.On the observability of target maneuvers via bearing-only and bearing-rate-only measurements.Proc.of the AIAA Guidance,Navigation,and Control Conference,1987:560–569.
[20]T.L.Song,T.Y.Um.Practical guidance for homing missiles with bearings-only measurements.IEEE Trans.on Aerospace and Electronic Systems,1996,32(1):434–443.
[21]J.H.Wilkinson.The algebraic eigenvalue problem.London: Oxford University Press,1965.
[22]Q.K.Wei,Z.G.Niu,B.Chen,et al.Airfoil roll control by bang-bang optimal control method with plasma actuators. Proc.of the AIAA Guidance,Navigation,and Control Conference,2012:1–15.
[23]T.Kim,C.Lee,M.Tahk.Time-to-go polynomial guidance with trajectory modulation for observability enhancement. IEEE Trans.on Aerospace and Electronic Systems,2013, 49(1):55–73.
Biographies

Shijie Fan was born in 1986.He received his M.S.degree from National University of Defense Technology,in 2008.He is currently a Ph.D.candidate at the National Key Laboratory of Automatic Target Recognition,National University of Defense Technology.His research interests include radar signal and data processing,maneuvering target tracking and data fusion.
E-mail:robertfsj@gmail.com

Hongqi Fan was born in 1978.He received his Ph.D.degree in information and communication engineering from National University of Defense Technology,in 2008.He is currently a lecturer at the National Key Laboratory of Automatic Target Recognition,National University of Defense Technology.His research interests include radar signal and data processing,target tracking,information fusion and multi-agent systems.
E-mail:fhongqi@gmail.com

Huaitie Xiao was born in 1966.He received his M.S.and Ph.D.degrees from National University of Defense Technology,in 1993 and 2000,respectively.He is currently a professor at the National Key Laboratory of Automatic Target Recognition, National University of Defense Technology.His research interests include automatic target recognition,radar signal processing and intelligent learning.
E-mail:htxiao@126.com

Jianpeng Fan was born in 1985.He is a lecturer at the College of Electronic Science and Engineering,National University of Defense Technology.His research interests include automatic target recognition,radar signal processing and target tracking.
E-mail:jpfan@nudt.edu.cn

Qiang Fu was born in 1962.He received his Ph.D. degree in information and communication engineering from National University of Defense Technology,in 2004.He is currently a professor at the National Key Laboratory of Automatic Target Recognition,National University of Defense Technology. His research interests include radar system design, precise guidance and automatic target recognition.
E-mail:fuqiang1962@vip.sina.com
10.1109/JSEE.2015.00017
Manuscript received March 17,2014.
*Corresponding author.
This work was supported by the National Natural Science Foundation of China(61101186)and the Specialized Research Fund for the Doctoral Program of Higher Education(20134307110012).
 Journal of Systems Engineering and Electronics2015年1期
Journal of Systems Engineering and Electronics2015年1期
- Journal of Systems Engineering and Electronics的其它文章
- Dynamic channel reservation scheme based on priorities in LEO satellite systems
- Adaptive beamforming and phase bias compensation for GNSS receiver
- Novel dual-band antenna for multi-mode GNSS applications
- Nonparametric TOA estimators for low-resolution IR-UWB digital receiver
- Effcient hybrid method for time reversal superresolution imaging
- Adaptive detection in the presence of signal mismatch
