Stability of GM(1,1)power model on vector transformation
Jinhai Guo,Xinping Xiao,Jun Liu,and Shuhua Mao
1.School of Science,Wuhan University of Technology,Wuhan 430072,China;
2.School of Information and Mathematics,Yangtze University,Jingzhou 434023,China
Stability of GM(1,1)power model on vector transformation
Jinhai Guo1,2,Xinping Xiao1,∗,Jun Liu1,and Shuhua Mao1
1.School of Science,Wuhan University of Technology,Wuhan 430072,China;
2.School of Information and Mathematics,Yangtze University,Jingzhou 434023,China
The morbidity problem of the GM(1,1)power model in parameter identifcation is discussed by using multiple and rotation transformation of vectors.Firstly we consider the morbidity problem of the special matrix and prove that the condition number of the coeffcient matrix is determined by the ratio of lengths and the included angle of the column vector,which could be adjusted by multiple and rotation transformation to turn the matrix to a well-conditioned one.Then partition the corresponding matrix of the GM(1,1)power model in accordance with the column vector and regulate the matrix to a well-conditioned one by multiple and rotation transformation of vectors,which completely solve the instability problem of the GM(1,1)power model.Numerical results show that vector transformation is a new method in studying the stability problem of the GM(1,1)power model.
grey power model,stability,morbidity,vector transformation,condition number of matrix.
1.Introduction
A slight observation error or a calculation rounding error may lead to a large output error in the data processing of engineering control,surveying adjustment model, economic and statistical analysis.That is the coeffcient drift which leads to system instability.The system instability problem is also known as the morbidity problem in some references,and the two appellations will not be made a distinction below.The GM(1,1)power model is an important nonlinear grey model.The traditional GM(1,1)and Verhulst model[1,2]are the special forms of the GM(1,1) power model.The element in the data matrix is generally obtained by observation and calculation in the practical application,and the minor error exists inevitably,then it may have a prominent effect on the process of parameter identifcation.If the condition number of the coeffcient matrix B of the GM(1,1)powermodel is verylarge(larger than 1 000),the slight change or rounding error in calculation tends to bring a huge error to modeling results[3,4].
The grey model morbidity problem has already been researched by some scholars.Zheng et al.[5]pointed out that it is diffcult to overcome the morbidity of the grey model,which should be cared in application.Zeng et al.[6]used multiple transformation to study the morbidity problem of the accumulating method GM(1,1).Dang et al.[7]discussed the possible situation of morbidity of GM(1,1).Xiao et al.[8]employed affne transformation to control the condition number of the coeffcient matrix of GM(1,1).Wu et al.[9,10]studied the GM(1,1)and discreted GM(1,1),made the raw data less than one through multiple transformation,and the morbidity problem was solved effectively.Wang et al.[4]estimated the condition number of the power model by the matrix element size and analyzed the reason why morbidity occurs.
The current research on the grey model morbidity problem is mainly analyzing its existence reason by estimating the condition number and applying multiple transformation to reduce the condition number[11–13].However, the Verhulst model morbidity problem has not been studied till now.Because of the complexity of exponent and time response formula,the GM(1,1)power model morbidity problem[14,15]has not been addressed yet.Under the direction of[16],of this paper proposes a new method to solve the morbidity problem,i.e.,for general two columns matrix B,we apply multiple and rotation transformation to column vectors to turn the matrix BTB into a wellconditioned one.As the coeffcient matrix of the GM(1,1) power model has column sums vector two,we can use the vectors transform to the matrix for solving the morbidity problem of the model.
The paper is structured as follows.In Section 2,for the general two columns matrix B,multiple and rotation transformation is applied to column vectors,the matrix BTB is turned into a well conditioned one.Section 3 partitions the coeffcient matrix of the GM(1,1)power model to col-umn vectors,gives an optimal value formula of the multiple value ρ by vector multiple transformation,then studies the relationship between the condition number and the power index of the power model matrix,analyzes the reason of morbidity and fnally provides a solving method of parameters of the GM(1,1)power model combining rotation transformation.Section 4 shows an example of calculating parameters and the condition number of the GM(1,1)power model by vector transformation.Section 5 concludes the paper.
2.Condition number of matrix based on vector transformation
The morbidity of a matrix is generally measured by the size of the condition number.The larger the number,the more serious the morbidity.For the general matrix B with two columns,we apply multiple and rotation transformation to column vectors below to reduce the condition number of BTB and turn it into a well-conditioned one.
2.1Defnition of condition number
Defnition 1is a matrix norm of[17],cond(A)=?A−1?.?A?is defned as the condition number of the matrix A.Since all matrix norms of A ∈Rn×nare equivalent,it is essentially consistent by using any norm to compute the condition number.For convenience,all the contents of this paper are discussed in 2-forms and cond2(A)=?A−1?2·?A?2.
When A is a normal matrix,the condition number of A is k(A)and k(A)=λ1/λ2,where λ1and λ2are respectively the maximum and minimum eigenvalues of the norm of A.Then,we have k(A)=k(aA),a∈R,a/=0.
k(·)is the condition number of?·?.If k(A)is large, then A is called the matrix inversion of the norm?·?or the morbid matrix in equation solution.If k(A)is small,then A is called the matrix inversion of the norm?·?or the wellill conditioned matrix in equation solution.In particular,A is an entirely well-conditioned matrix when k(A)=1.In practice,we generally consider that if 1<k(A)<10,A is in well condition;if 10≤k(A)<100,A is in mid-ill condition;if 100≤k(A)≤1 000,A is in moderate or strong-ill condition;if k(A)>1 000,A is in serious-ill condition[2,8,13].
2.2Condition number of multiple transformation
Theorem 1If X and Y are nonzero real vectors, B=(X,ρY),C=BTB,ρ is a constant and ρ>0. When?X?=ρ?Y?,the condition number k(C)of C will be the minimum and where θ is the included angle of X and Y.

Proof?X?2=XTX,?Y?2=YTY,XTY= ?X??Y?cosθ,where θ is the included angle of X and Y.
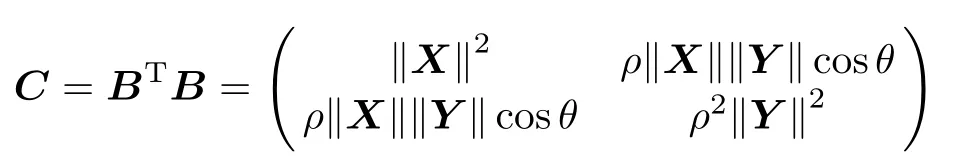
The eigenvalues of C are

The condition number is
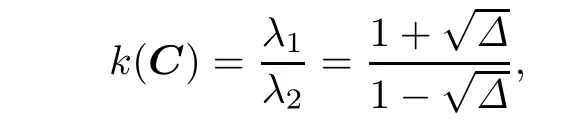
where
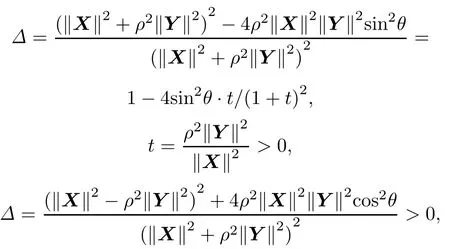
then Δ∈(0,1),the condition number k(C)is the monotone increasing function of Δ,and Δ achieves the minimum when t=1.That is to say,when?X?2=ρ2?X?2, the condition number achieves the minimum.We can get Δ=1−sin2θ=cos2θ,

Theorem 1 proves that the condition number of BTB is determined by the ratio of lengths and the included angle of the column vectors X and Y.When the lengths of X and Y are equivalent by multiple transformation,the condition number is minimum,and we can get the function relationship between the condition number of BTB and the included angle θ of X and Y.It can be derived that the range of corresponding θ with the condition number interval of BTB after the multiple transformation.The results are shown in Table 1.
From Table 1,when θ∈(35.10°,144.90°),the condition number of BTB can be reduced to less than 10and make it into a well-conditioned one through multiple transformation,which is not applied to the situation when θ/∈(35.10°,144.90°).Therefore we would use rotation transformation of vectors to solve this problem below.

Table 1 Range of the corresponding θ with the condition number interval
2.3Condition number of rotation transformation
Theorem 2If X and Y are nonzero real vectors,matrix B=(X,Y),constant ρ>0,?X?=?Y?=M, where θ is the included angle of X,Y.We have the results as follows:
(i)When θ∈(0°,35.10°),B∗=(c(X −Y),Y), where the constant c=?Y?/?X−Y?,the lengths of column vectors c(X−Y)and Y of the matrix B∗are equivalent now and the included angle θ∗of c(X−Y)and Y is θ∗=(90°+θ/2)∈(90°,107.55°)⊂(35.10°,144.90°), then the condition number of C∗=(B∗)TB∗is less than 10 and the matrix C∗is well-conditioned.
(ii)When θ∈(144.90°,180°),B∗=(c(X+Y),Y), where the constant c=?Y?/?X+Y?,the lengths of column vectors c(X+Y)and Y of the matrix B∗are equivalent now and the included angle θ∗of c(X+Y) and Y is θ∗=θ/2∈(72.45°,90°)⊂(35.10°,144.90°), then the condition number of C∗=(B∗)TB∗is less than 10 and the matrix C∗is well-conditioned.
Proof(i)When θ∈ (0°,35.10°),B∗=(c(X −Y),Y),?c(X−Y)?=c?X−Y?=?Y?,the lengths of column vectors of the matrix B∗are equal to M.
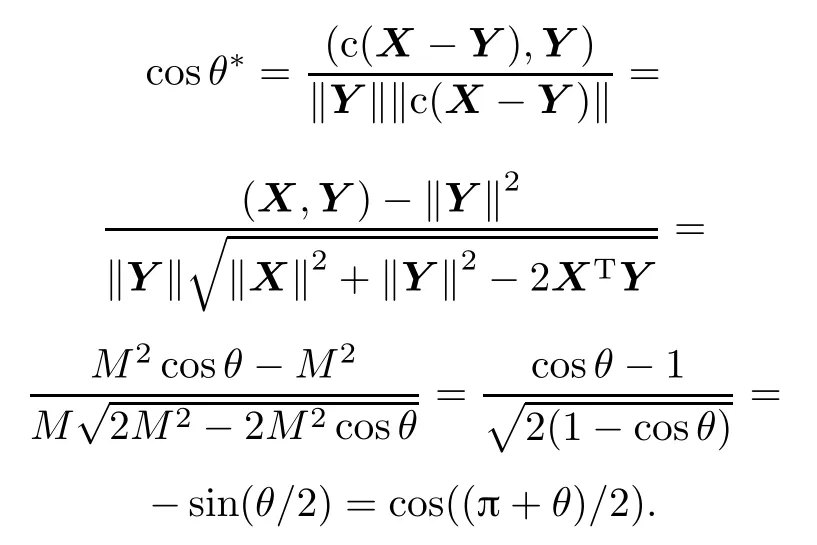
As cosθ∗is a single value function on the interval (0,π),therefore the included angle θ∗=(90°+θ/2)∈(90°,107.55°)⊂ (35.10°,144.90°)then the condition number of C∗=(B∗)TB∗is less than 10,and the matrix C∗is well-conditioned.
(ii)When θ ∈ (144.90°,180°),B∗= (c(X+ Y),Y),?c(X+Y)?=c?X+Y?=?Y?,the lengths of column vectors of the matrix B∗are equal to M.
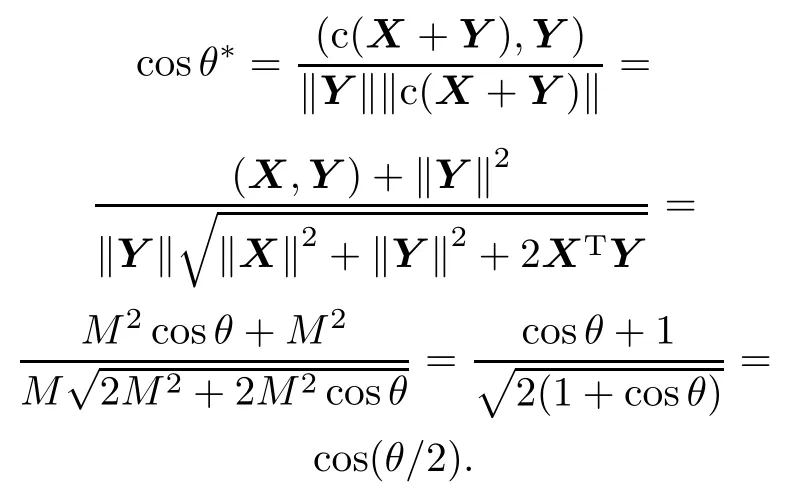
Therefore,the included angle θ∗= θ/2 ∈(72.45°,90°)⊂ (35.10°,144.90°),then the condition number of C∗=(B∗)TB∗is less than 10,and the matrix C∗is well-conditioned. ?
3.Stability analysis of GM(1,1)power model
In Section 2,for general two columns matrix B,vector transformation is used to turn the matrix BTB into a well-conditioned one.In the parameter identifcation of the GM(1,1)power model,the column of the coeffcient matrix B0is two,so the methodin Section 2 can be employed to solve the stability problem of the GM(1,1)power model.
To describe concisely,the following common symbols are listed below:
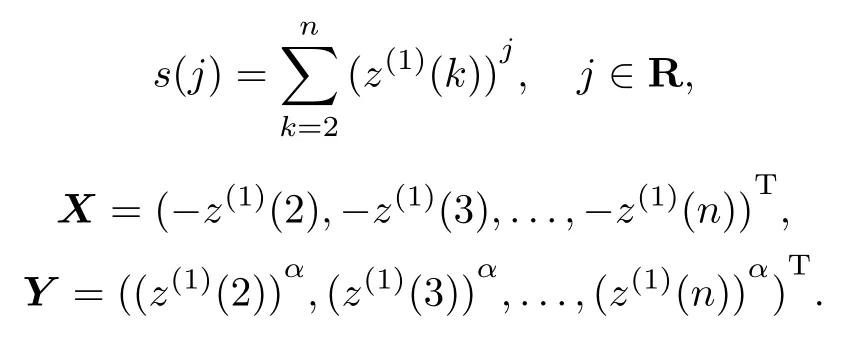
3.1Defnition of GM(1,1)power model
The defnition of GM(1,1)power model[2](referred to as the GPM hereinafter)is
GPM(1,1,D):x(0)(k)+az(1)(k)=b(z(1)(k))α
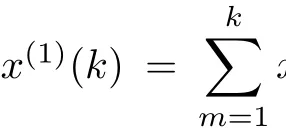
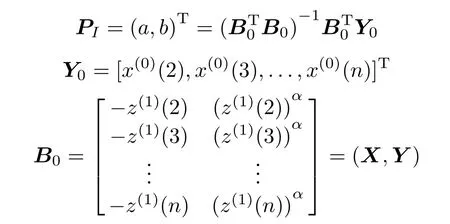

The time response of GPM is

From the inverse accumulated generating operation,we have
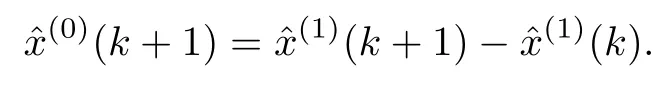
3.2Multiple transformation of GM(1,1)power model
In order to study the coeffcient matrix of the GM(1,1) power model,the relationship between the multiple transformation of series xi(i=1,2,...,n)and that of column vectors of the matrix is studied.
The transformation yi=ρxi(i=1,2,...,n)of series xi(i=1,2,...,n)(where ρ is a constant,ρ>0)is called multiple transformation.ρ is called the multiple number. The modeling steps of grey power model whose accumulated generating operation series have multiple transformations are as follows.
Let X(0)=(x(0)(1),x(0)(2),...,x(0)(n))be raw series,X(1)=(x(1)(1),x(1)(2),...,x(1)(n))is said to be accumulated generating operation(AGO)series of X(0), written as X(1)=AGOX(0),provided that X(1)= (x(1)(1),x(1)(2),...,x(1)(n)),where

Let the coeffcient matrix Byby multiple transformation
yi=ρxias
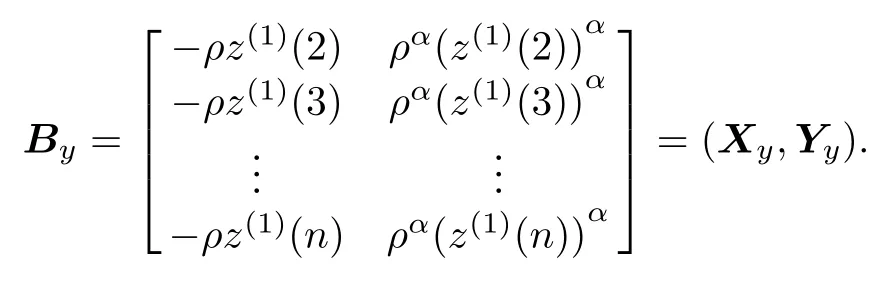
Let B=(X,ρα−1Y),then By=ρ(X,ρα−1Y)= ρB,Cy=BTyBy=ρ2BTB,it can be deduced that k(Cy)=k(ρ2BTB)=k(BTB)by Defnition 1 about the condition number.Then,we will study the condition number of the matrix BTB,and the calculation formula of multiple value ρ is obtained by Theorem 1 as follows.
Theorem 3GM(1,1)power model GPM(1,1,D):
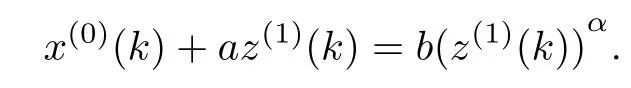
Do multiple transformation on raw series yi=ρxi(i= 1,2,...,n).When ρ=(s(2α)/s(2))1/(2−2α),the condition number of the matrix Cy=BTyByreaches the minimum
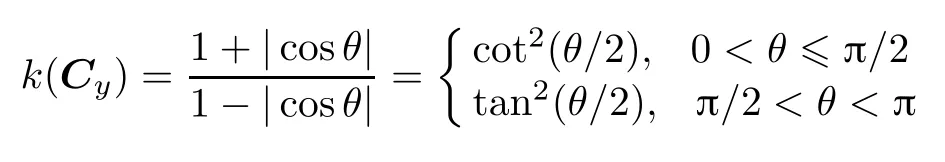
where θ is the included angle of X and Y.
ProofAccording to Theorem 1,when B = (X,ρα−1Y),the condition number of BTB will reach the minimum.
Since?X?=?ρα−1Y?,that is?X?2=?ρα−1Y?2, i.e.,s(2) = ρ2α−2s(2α).This means when ρ = (s(2α)/s(2))1/(2−2α),the condition number of BTB reaches the minimum.
Therefore,the condition number of the matrix Cy= BTyByalso reaches the minimum


3.3Relationship between condition number and power exponent of matrix
By Theorem 3,we know multiple transformation can reduce the condition number of the power model matrix and the condition number is only related to the included angle of X and Y.If the raw series xi(i=1,2,...,n)is given,the included angle θ of X and Y is the function on the power exponent α.Thus the condition number is the function on the power exponent α.Now,we will study the relationship between the condition number and the power exponent of the power model matrix.
Theorem 4Let θ be the included angle of X and Y, then cos2θ=(s(α+1))2/(s(2)s(2α)).When α< 1, h(α)=cos2θ is monotone increasing on the power exponent α;when α>1,h(α)is monotone decreasing on the power exponent α.
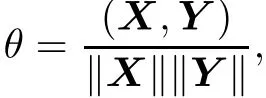

Calculate the derivative of α,there is
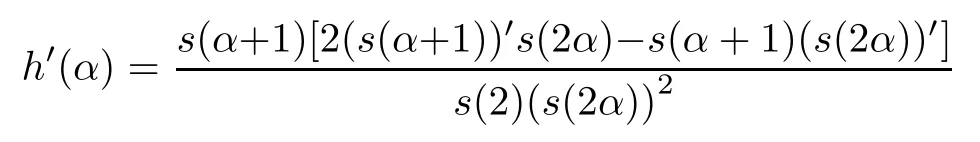
where
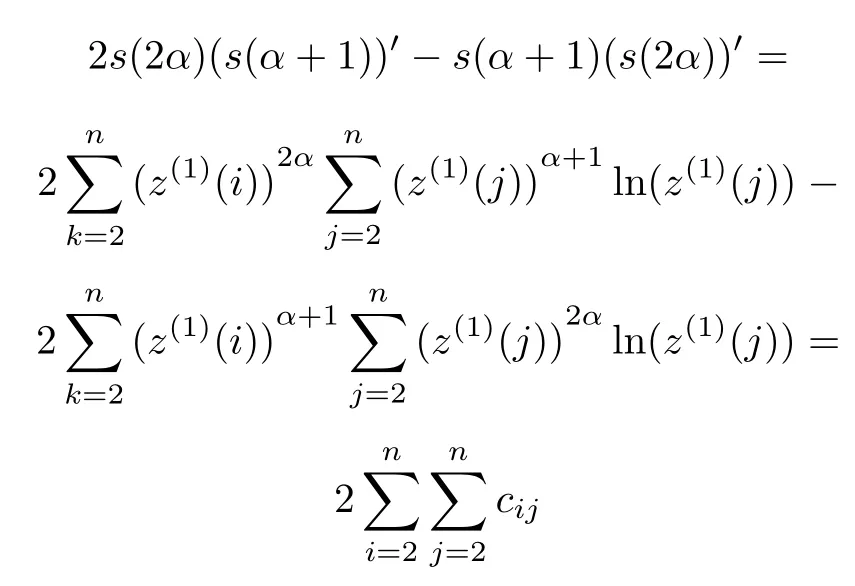
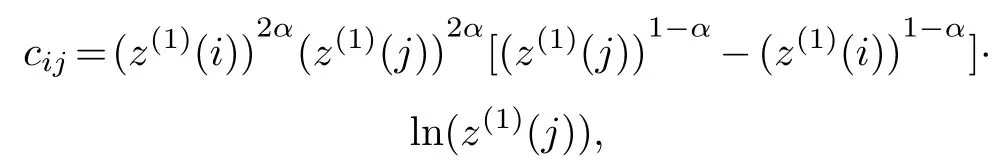
Thus we can get
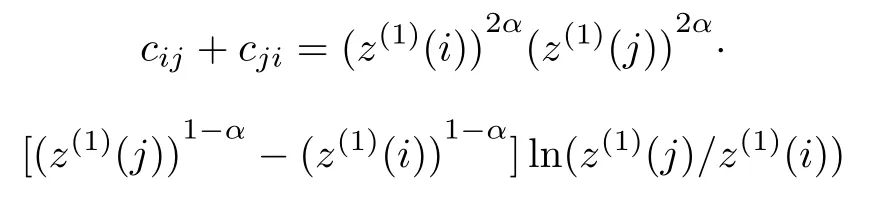
when i=j,cii=0,i=2,...,n.Mark
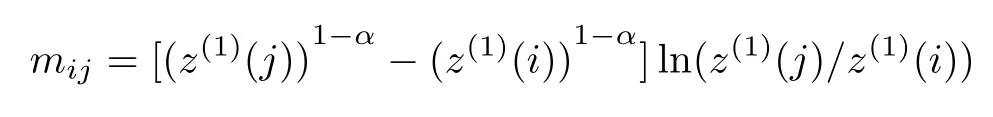
if z(1)(j)/= z(1)(i),when α < 1,mij> 0;when α>1,mij<0.
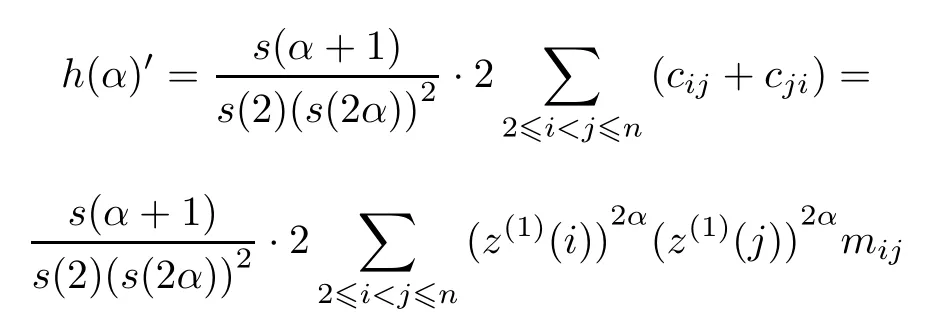
As(z(1)(2),z(1)(3),...,z(1)(n))is not a constant series,the values of mijare not all zero,and s(α+ 1),s(2),s(2α),z(1)(i)are all greater than zero,then we have the results that when α < 1,h(α)′> 0;when α>1,h(α)′<0.
Therefore when α<1,h(α)is monotone increasing on the power exponent α.On the contrary,when α>1,h(α) is monotone decreasing on the power exponent α. ?
From Theorem 3,when the lengths of coeffcient matrices column vectors are equivalent,the condition number is a function of the included angle of vectors,
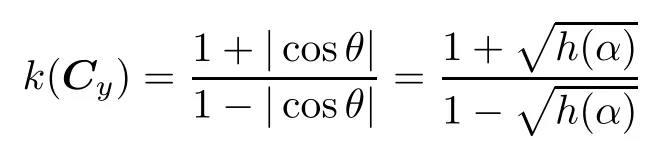
When the power exponent α→ 1,we have Y →−X,the included angle of X and Y,θ→ π,|cosθ|→1,k(Cy)→ +∞.Fig.1 shows the relationship between the condition number(cond)and the power exponent(α) of the power model after multiple transformation,which illustrates that when the power exponent α→ 1,multiple transformation alone could not turn the matrix into a well-conditioned one.Thus rotation transformation will be applied to reduce the condition number of the matrix continuously to make the matrix well-conditioned below.

Fig.1 Relationship between cond and α after multiple transformation
3.4Rotation transformation of GM(1,1)power modelIn GPM(1,1,D),multiple number ρ=(s(2α)/s(2))1/(2−2α)according to Theorem 3,and By= (Xy,Yy) = (ρX,ραY)after multiple transformation yi= ρxi. Because the values of z(1)(i)are all greater than zero, then XTY < 0,therefore the included angle of X and Y is greater than 90°.When the condition number of the matrix Cy=BTyByis greater than 10,then θ∈ (144.90°,180°)by Table 1.Make rotation transformation B∗=(c(Xy+Yy),Yy)through Theorem 2, where c=?Yy?/?Xy+Yy?,then?c(Xy+Yy)?=?Yy?. Making equivalent transformation of the power model
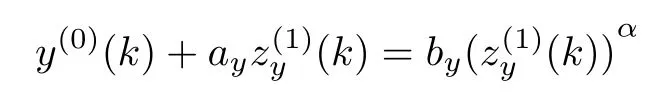
after multiple transformation,we can get
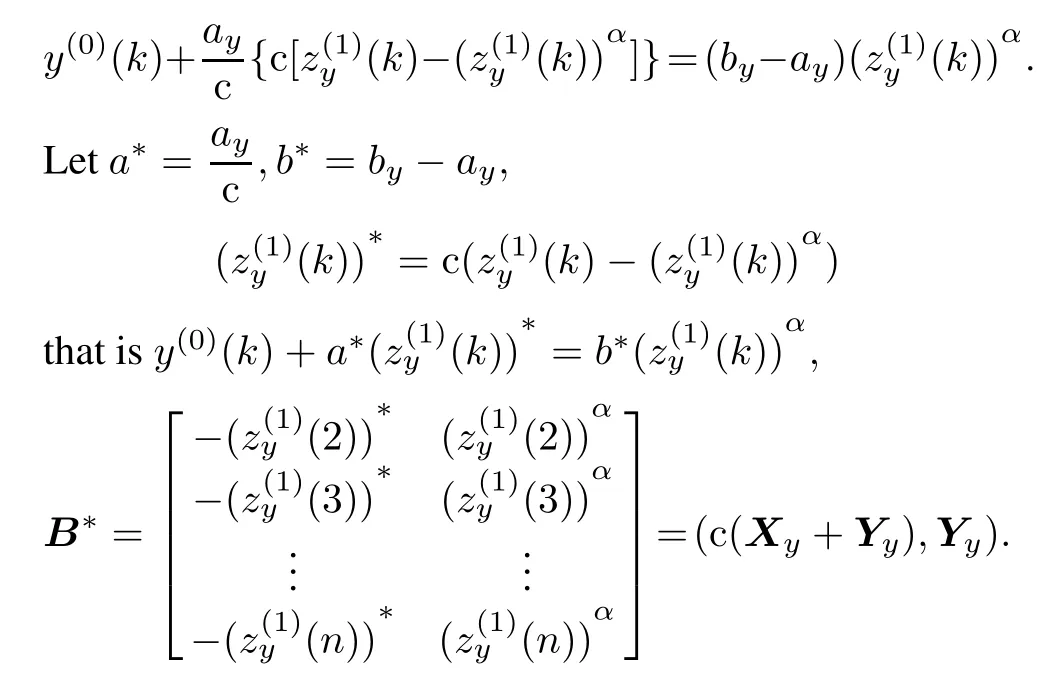
From Theorem 2,the condition number of C∗= (B∗)TB∗is less than 10,and C∗is a well-conditioned matrix.
We use the following three steps to solve parameters of the power model by vector transformation:
Step 1Let ρ=(s(2α)/s(2))1/(2−2α),make multiple transformation of raw series yi=ρxi(i=1,2,...,n), we can get the coeffcient matrix By=(ρX,ραY)= (Xy,Yy).If the condition number of the matrix Cy= BTyByis less than 10,go to Step 3;If not,go to Step 2.
Step 2Make rotation transformation to get the coeffcient matrix B∗=(c(Xy+Yy),Yy),where the constant c=?Yy?/?Xy+Yy?.By the least square method,we have
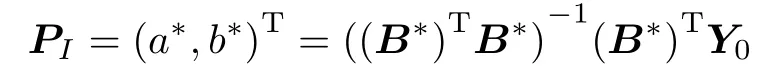
to obtain the parameters a∗and b∗.Substitute c in a∗= ay/c,b∗=by−ayto obtain parameters ayand by;
Step 3Calculate the parameters a and b by formula ay=a,by=ρ1−αb after multiple transformation[1],fnally bring it into the white response of the GM(1,1)power model.
4.Example analysis
We use the method of[15]and the optimization model 1 in [18]to identify the power exponent of the GM(1,1)power model respectively to simulate the proportion of Chinese high school graduates and compute the condition number. Table 2 providesthe data of the Chinese proportionof high school graduates from 1999 to 2008.
Data are derivedfrom the website of National Bureauof Statistics of China.
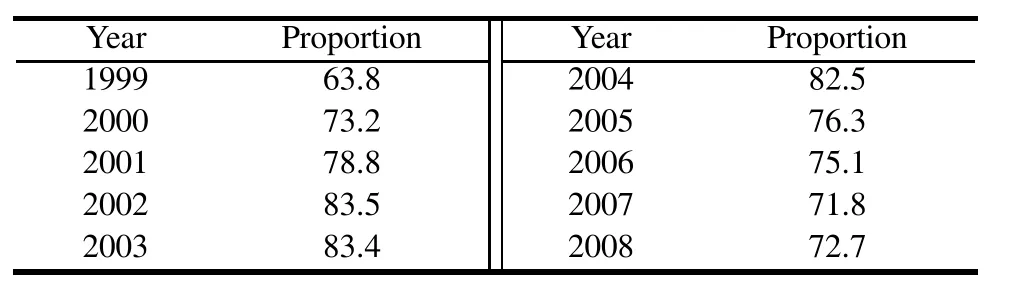
Table 2 Proportion of Chinese high school graduates from 1999 to 2008 (%)
Take the data from 1999 to 2006 as the raw series
X(0)=[63.8,73.2,78.8,83.5,83.4,82.5,76.3,75.1].
(i)We get α=−0.019 9 through the power exponent formula of[12].
(ii)According to the optimization power exponent (model 1)in[15],the optimal value α=0.3.
(iii)When the power exponent α→1,k(Cy)→+∞. In order to study the condition number,we chose a power exponent α approximating to 1 and α=0.99.
According to the above three steps,we can get the condition number under multiple and rotation transformation for different power exponent α(see in Table 3).In Table 3, MT,RT,and CN represent the multiple transformation,rotation transformation and condition number,respectively. We also get the parameter value for different power exponent α(see in Table 4).

Table 3 Date of condition number after multiple and rotation transformation under different α
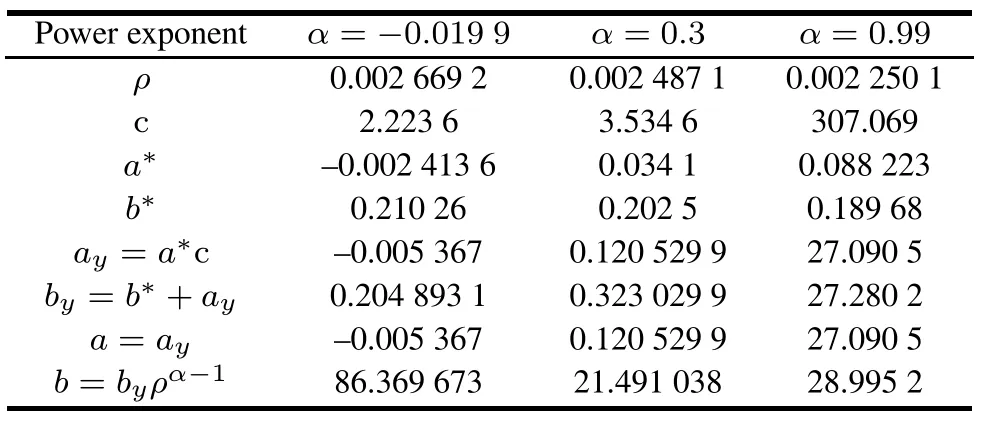
Table 4 Values of parameters under different α
Table 3 shows:after multiple transformation,when the power exponent α<1,the condition number is monotone increasing on the power exponent,and when α=0.99 is approximate to 1,the condition number is 377 160 which is still very large;using multiple transformation alone does not necessarily reduce the condition number of the matrix to less than 10,so making a matrix well-conditioned requires the aid of rotation transformation;after multiple and rotation transformation,the condition numbers ofthe matrix are all less than 10,and the matrix is a wellconditioned one.
5.Conclusion and discussion
As the value of the power exponent α is multiform,the form of the GM(1,1)power model is diversity.If the stability problem of the power model is studied fully,the stability of special circumstances are also solved,such as GM(1,1)power model and Verhulst model.The method by vector transformation is proposed which solves the morbidity problem of the matrix corresponding to the matrix with two columns.This method not only settles the stability problem of the GM(1,1)power model but also provides an effective approach to solve the stability problem of other grey models whose column of the coeffcient matrix is two. While the stability problem of grey models whose column of the coeffcient matrix is more than two should be further discussed.
[1]J.L.Deng.Introduction to grey systems theory.Journal of Grey System,1989,1(1):1–24.
[2]X.P.Xiao,Z.M.Song,F.Li.Element and application of grey technology.Beijing:Science Press,2005.
[3]Q.F.Li,Y.G.Dang,Z.X.Wang.An extended GM(1,1) power model for non-equidistant series.Journal of Grey System,2012,24(3):269–274.
[4] Z.X.Wang.Research on the buffer operators with parameters and GM(1,1)power model.Nanjing:Nanjing University of Aeronautics and Astronautics,2010.
[5]Z.N.Zheng,Y.Y.Wu,X.H.Chen,et al.The illness problem in grey models.Systems Engineering−Theory Methodology Applications,2001,10(2):140–144.(in Chinese)
[6]X.Y.Zeng,X.P.Xiao.Research on morbidity problem of accumulating method GM(2,1)model.Systems Engineering and Electronics,2006,28(4):542–544.(in Chinese)
[7]Y.G.Dang,Z.X.Wang,S.F.Liu.Study on morbidity problem in grey model.Systems Engineering−Theory&Practice, 2008,l28(1):156–160.(in Chinese)
[8]X.P.Xiao,S.K.Tong,S.H.Mao.Research on ill-conditioned problem in grey prediction control model.Proc.of the 3rd International Conference on Machine Learning and Cybernetics, 2004:2010–2013.
[9]Z.P.Wu,B.Li,Y.P.Zhang,et al.Study on the morbidity problem in grey model.Journal of Communication University of China(Science and Technology),2011,18(4):31–34.(in Chinese)
[10]Z.P.Wu,S.F.Liu,Y.G.Dang,et al.Study on the morbidity problem in grey model.Systems Engineering−Theory& Practice,2011,31(1):108–112.(in Chinese)
[11]Y.Shao,Y.Wei,H.J.Su.On approximating grey model GM(2,1).Journal of Grey System,2010,22(4):333–340.
[12]X.Y.Zeng,X.P.Xiao.A research on morbidity problem in accumulation method GM(1,1)model.Proc.of the 4th International Conference on Machine Learning and Cybernetics, 2005:18–21.
[13]C.F.Li,Y.X.Shu,C.J.Rao.Morbidity analysis on grey forecast model.IEEE Symposium on Knowledge Acquisition and Modeling Workshop,2008:348–351.
[14]J.L.Li,X.P.Xiao.GM(1,1)power model based on particle swarm optimization algorithm.Computer Engineering and Applications,2008,44(32):15–18.
[15]Z.X.Wang,Y.G.Dang,S.F.Liu,et al.Solution of power model and its properties.Systems Engineering and Electronics,2009,31(10):2380–2382.(in Chinese)
[16]Y.H.Wang.Morbid matrix’s essence and its solutions.Mine Surveying,2005,6(2):62–63.(in Chinese)
[17]Z.Xu,K.Y.Zhang,Q.Lu,et al.The concise course on matrix. Beijing:Science Press,2005.
[18]Z.X.Wang,Y.G.Dang,J.J.Zhao.Optimized GM(1,1)power model and its application.Systems Engineering−Theory& Practice,2012,32(9):1973–1978.(in Chinese)
Biographies

Jinhai Guowas born in 1980.He received his B.S. degree in the School of Mathematics and Computers from Hubei University,Wuhan,China,in 2001.He received his M.S.degree in fundamental mathematics from Wuhan University in 2004. He is currently working toward his Ph.D.degree at Wuhan University of Technology.His research interests are grey system theory and application.
E-mail:xin3fei@21cn.com

Xinping Xiao was born in 1965.He received his Ph.D.degree in systems engineering from Huazhong University of Science and Technology in Wuhan,China.He is now a professor and deputy dean of the School of Science,Wuhan University of Technology.He has published three books on grey system and over 100 journal papers.His research interests lie in grey system,systems engineering,and graph theory and control technology.
E-mail:xiaoxp@263.net

Jun Liu was born in 1964.He received his B.S.degree in applied mathematics from Huazhong Normal University,Wuhan,China in 1987.He received his M.S.degree in applied mathematics from Central South University,Changsha,China in 1997.He is currently working toward his Ph.D.degree at Wuhan University of Technology.His research interests are grey system theory and application.
E-mail:mailliujun@126.com

Shuhua Mao was born in 1973.He received both his B.S.degree and M.S.degree in applied mathematics from Wuhan University of Technology in 2004 and 2011,respectively.He is currently an associate professor in Wuhan University of Technology.His research interests lie in grey system theory and application,and data processing and system optimization of intelligent transportation system.
E-mail:maoshuhua@sina.com
10.1109/JSEE.2015.00014
Manuscript received March 01,2013.
*Corresponding author.
This work was supported by the Specialized Research Fund for the Doctoral Program of Higher Education of China(20120143110001),the General Education Program Requirements in the Humanities and Social Sciences of China(11YJC630155),and the Youth Foundation of Hubei Province of China(Q20121203).
 Journal of Systems Engineering and Electronics2015年1期
Journal of Systems Engineering and Electronics2015年1期
- Journal of Systems Engineering and Electronics的其它文章
- Dynamic channel reservation scheme based on priorities in LEO satellite systems
- Adaptive beamforming and phase bias compensation for GNSS receiver
- Novel dual-band antenna for multi-mode GNSS applications
- Nonparametric TOA estimators for low-resolution IR-UWB digital receiver
- Effcient hybrid method for time reversal superresolution imaging
- Adaptive detection in the presence of signal mismatch
