一种CORDIC协处理器核的设计与实现

邓凌煊 ， 安军社

（1.中国科学院大学 北京 100190；2.中国科学院 空间科学与应用研究中心，北京 100190）

随着航天技术的发展，航天任务对于导航计算机的性能要求越来越高。导航计算机除了要对传感器数据进行采集，与控制系统进行实时通讯，还要能进行实时的计算[1]。尽管目前航天任务中使用的处理器芯片性能越来越强，但大多数CPU并没有处理常用超越函数（sin，cos，arctan，exp，sqrt，ln 等）的专用指令。而通过纯软件循环迭代求解超越函数往往需要CPU数十甚至上百个周期[2]，这极大降低了导航计算机的实时性。本文提出了一种高实时性、低复杂度的CORDIC协处理器核，提供了高吞吐率的超越函数运算能力，从而提高了导航计算机的并行运算能力。此IP核使用verilog编写,由于其资源占用率低，可以非常容易地被集成入各种航天用FPGA中。

1 CORDIC算法

1.1 CORDIC旋转

CORDIC算法最早由Volder提出[3]，用于求解一般三角函数，之后由Walther改进[4]，使得CORDIC可以用于计算双曲函数和进行乘除运算。由于几乎所有的通用CPU都具有硬件乘法除法功能,因此对数坐标模式所提供的乘除功能很少被实际使用,故CORDIC算法的主要应用是三角函数和双曲函数的运算。CORDIC的基本思想是通过一系列预定大小角度的旋转，使得输入向量被旋转到所期望的位置，从而求解出一系列函数。CORDIC的旋转方程可以表示为

其中m为1时CORIDC工作在圆坐标系下，m为-1时工作在双曲坐标系下。dn为1时向量按顺时针方向旋转，当dn为-1时按逆时针方向旋转。

虽然每一步迭代只需要进行加减操作和固定位的移位操作，但由（1）可知，CORIDC每一次旋转都会改变向量的模。所以为了得到正确的向量分量x和y，需要补偿旋转后的向量，而由于向量模的变化与旋转的方向无关，这可以通过一个常数乘法器实现。补偿常数为：

CORDIC每次旋转的方向由工作模式决定。在旋转模式下，CORDIC试图让向量与x轴之间的夹角z趋近于0。在向量模式下，CORDIC试图让向量的y分量趋近于0。故每次旋转的方向由运行模式和向量的yz分量符号决定：

综上，各个模式下CORDIC的迭代结果以及可实现的函数如表1所示。

表1 各模式CORDIC旋转结果Tab.1 Rotation result of CORDIC under all modes

1.2 收敛性

Cordic能输出正确结果的前提是旋转结束时向量能够被旋转到预期的位置（在误差范围内），即旋转收敛。可以通过递归证明的是[5]，对于圆坐标模式，对于任意n总有

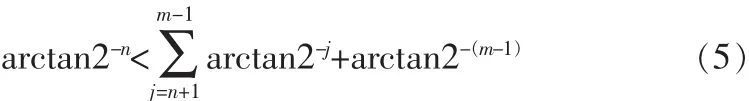
令剩余角度为rn+1，

总rn<2·arctan2-n有。但是对于双曲坐标模式，类似的结论并不成立。然而可以证明的是

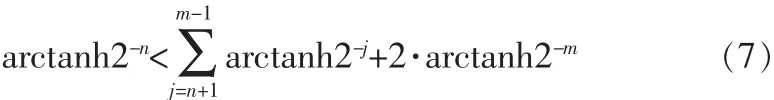
对于m=3i+1，i=1，2，3…成立。故对于双曲坐标模式，为了保证算法收敛，需要将第4，13，40...次循环重复。此外，由于在每一级旋转的角度是预先固定的，故CORDIC所能将向量旋转的角度有限，即系的收敛域分别为A∈[-1.743，1.743]，对于双曲坐标模式为A∈[-1.055，1.055]。

2 系统实现

为了保证协处理器能够提供足够的计算吞吐量并使协处理器的计算延迟可预测，本文使用流水线实现整个CORDIC核[6]。协处理器的流水线结构如图1所示。

2.1 系统输入

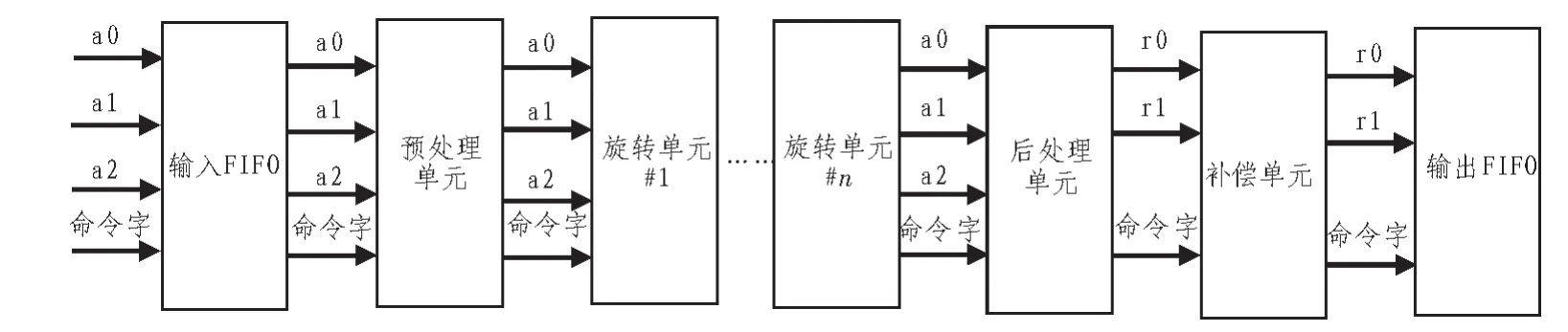
图1 CORDIC协处理器流水线框图Fig.1 Pipeline structure of CORDICcoprocessor

协处理器核从输入FIFO获得初始输入数据，包括3个坐标分量以及1个控制命令字。输入参数的格式为1位符号位，2位整数位，小数位的位数作为IP核的参数可以在例化时调整。这样的输入格式使得此IP核可以容易地被应用于使用定点运算的许多DSP处理器。对于浮点数运算，实际上CPU可以通过简单的移位缩放操作使得输入范围外的xyz分量落到协处理器可接受的范围内，这是由于规格化浮点数的尾数本来就在区间[1，2）内。相对的，已有的很多CORDIC协处理器实现[7]使用了浮点数进行中间运算，然而这不仅显著地增加了资源的使用，而且使得每一个CORDIC旋转需要通过多级流水线完成，增大了每个运算的延迟。

此外，为了降低CPU和协处理器之间交互次数，本IP核允许CPU在计算某些函数时不对所有的输入寄存器进行写入。对于输入参数少于3个的函数，协处理器自动生成其他分量的输入。比如对于cos（x），CPU只需要对协处理器的a0寄存器和控制字寄存器写入即可触发cos（x）的运算，CORDIC协处理器会自动把x分量初始化成2.0，y分量初始化成0，z分量初始化成a0。对于有效位数较小的配置如18位，可以进一步将控制命令字和a0放到同一个32位寄存器中，则对于单输入函数，CPU只需向一个地址写入数据即可完成操作。18位数据精度时的输入寄存器格式如图2所示。

图2 18位配置时的CORDIC核输入寄存器Fig.2 Input register of CORDICcore under 18 bits configuration

2.2 预处理单元

如表1所示，CORDIC的运算结果并不直接对应所要求的函数，故需要对与输入参数进行处理。例如对于ln（a）和sqrt（a）运算，需要令 x=a+1，y=a-1，对于 cos（x），sin（x）等运算，需要生成相应的其他分量输入。此外，由于双曲坐标的性质，arctanh1并不存在，故双曲坐标模式只能从i=1开始迭代，而圆坐标系可以从i=0开始迭代，这导致了两种模式的旋转过程不同。为了能用同一个流水线实现2种模式的操作，本文令所有模式都从i=1开始迭代。但这样会导致在圆坐标模式下的收敛域过小，只有。解决的办法是在预处理单元加入象限折叠，即通过三角函数关系，将[-π，π]上的向量折叠到[0，]上，再在后处理单元对结果进行修正。

2.3 旋转单元

旋转单元是CORDIC协处理器的核心，实现（1）所描述的向量旋转操作。其结构如图3所示。

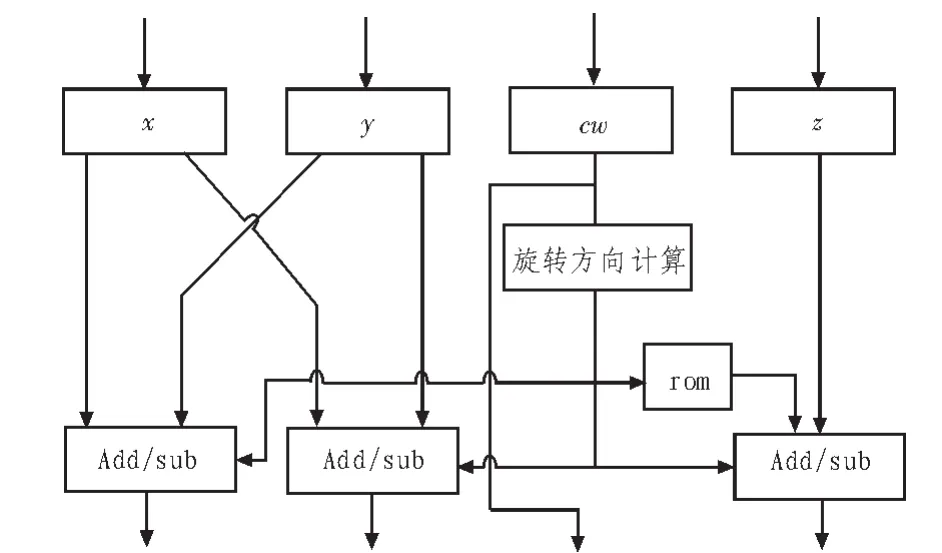
图3 CORDIC旋转单元的原理图Fig.3 Schematic sheet of CORDICrotation unit

此模块首先通过控制命令字、yz分量计算出旋转的方向，然后对向量作旋转。由于圆坐标和双曲坐标模式下旋转的角度不同，所以需要根据控制命令字进行选择。由于使用了流水线结构，移位操作实际上通过布线而静态确定，不需要专门的移位器。模块使用3个可进行加减运算的ALU单元分别对xyz分量进行修正。Rom存储了圆坐标和双曲坐标模式下的旋转角度，其精度根据IP核的配置而定，可以简单地通过在实例化verilog模块时指定参数来进行配置。

2.4 后处理单元

由图2可知，旋转单元的输出结果并不直接对应CORDIC协处理器所提供的函数。后处理单元对CORDIC旋转单元的输出结果进行处理，实现所需要的函数。具体的处理如表2所示。

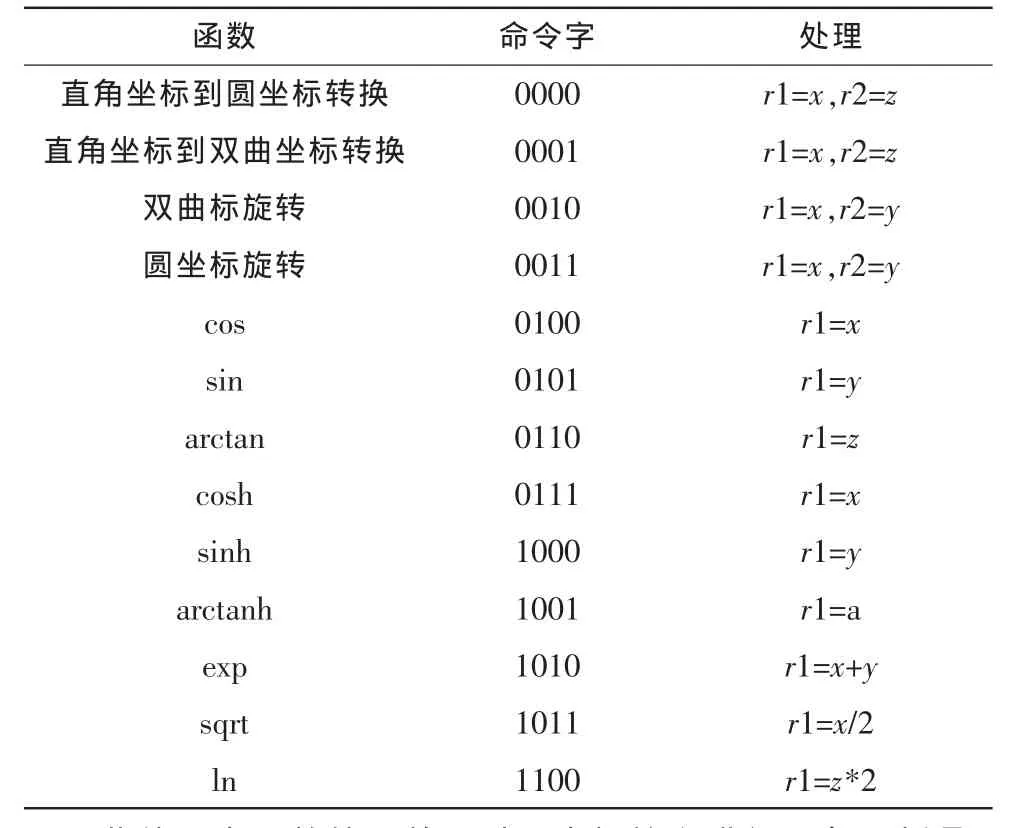
表2 命令字对应的输出处理Tab.2 Control words and corresponding post processing operations

此外，由于前处理单元对圆坐标输入进行了象限折叠，后处理单元需要进行相应的修正。例如对于圆坐标旋转模于是相应的后处理单元需要将x和y的值相交换。

2.5 补偿单元

由（4）可知，CORDIC每次旋转都会改变向量的模，故需要对最终的xy分量进行补偿。由于向量模变化只与坐标系模式有关，故补偿单元可以用一个常数乘法器实现。常数乘法器可以通过用华莱士树把移位后几个向量相加来实现。本文在线下通过程序穷举找出了一组加减操作数最少乘数编码方式，对于18位的配置，可以使用一个9输入的华莱士树和一个加法器实现，这使得该核在缺乏硬件乘法器的基于flash的Actel FPGA上也可以轻松使用。华莱士树中一位的结构如图4所示。

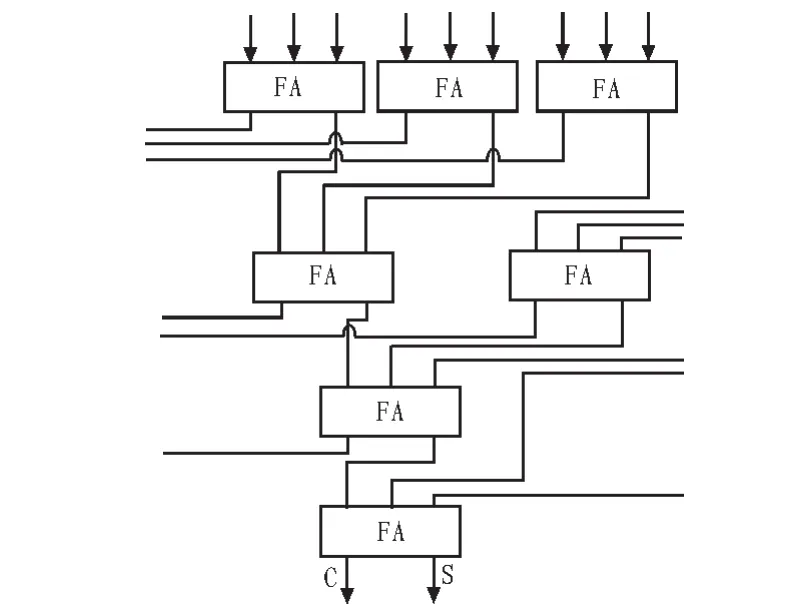
图4 9位华莱士树结构Fig.4 The structure of a 9 input Wallace tree

3 性能分析

为了证明所提出的IP核的实用性，本文选取了迭代次数16-20，扩展位数为5位的几种配置进行了综合。综合平台使用了航天电子系统常用的2种 FPGA：A3P3000E和xc4vf40。综合结果如表3所示。

可见本IP核具有较高的性能和较低的资源占用率，可以较容易地被集成，且随着迭代次数和精度的提高，资源的增长趋势稳定，速度的下降并不明显。

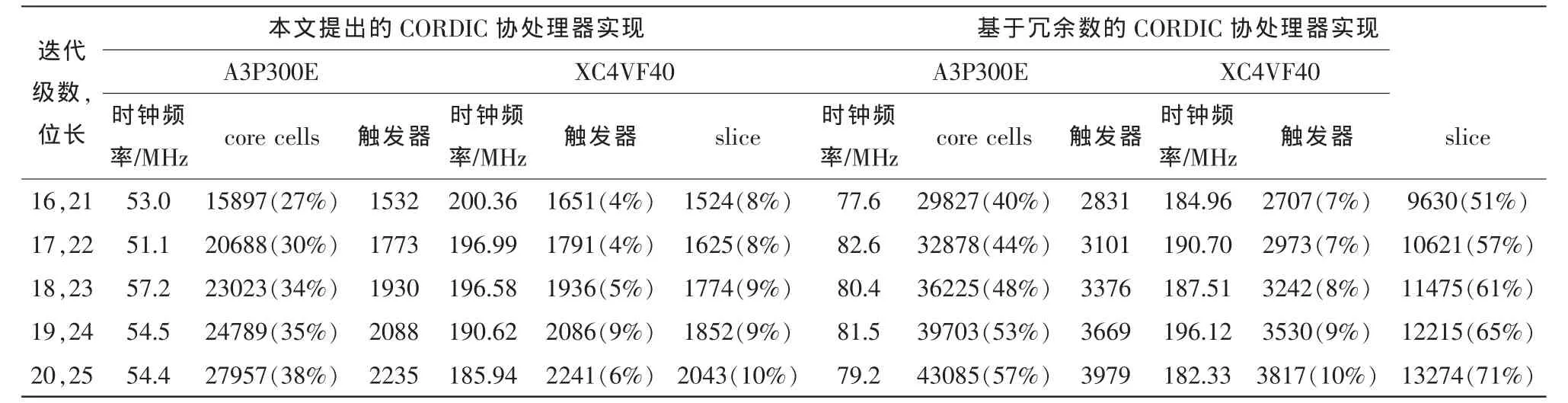
表3 本文提出的CORIDC协处理器实现与基于冗余数实现方案的综合对比Tab.3 Comparison between proposed CORDIC coprocessor and redundant arithmetic based

一直以来有很多为加速CORDIC运算而提出的方法，其中很多使用了冗余数，试图通过冗余数进位传播有限的特点来降低加法器的延迟。但本文通过对比发现，基于冗余数的算法仅在A3P3000E的实现上有一定速度优势，而在virtex4上没有速度优势，还在资源利用率上有很大劣势。原因是当前的大多数FPGA针对常见运算逻辑，如加法器的实现作出了特殊优化，使用了快速进位链降低加法器的进位延迟。相对的，由于FPGA缺乏对冗余数逻辑的支持，冗余数加法器需要由基本单元综合生成，具有较大的布线延迟，且需要消耗大量的LUT或逻辑门资源。此外，由于冗余数使用2倍于补码长度的编码方式来表示数值，冗余数需要使用更多的寄存器寄存每级流水线的中间结果。综上，对于有效位数较少的配置，本文提出的CORDIC协处理器具有更好的性能与资源利用更具优势。

4 精度与误差

根据参考文献[8]可知，CORDIC计算的误差主要来自2部分：由于每次迭代时用来修正z分量的角度有限而产生的近似误差和由于计算位数有限而产生的xy分量截断误差。为了尽量降低误差，首先应该保证旋转过程中用来修正z的数值是经过舍入得到的，而不是简单通过截断得到的，这样可以减小由于使用近似的旋转角度而产生的舍入误差。其次可以考虑在最终阶段运算结果前进行舍入。运算结果的舍入可以在补偿单元通过增加华莱士树的输入实现。即增加一个输入变量，其大小为最低有效位的一半，符号与补偿单元的输入相同。除此之外，需要根据所需的精度合理选择CORDIC协处理器的数据位数，增加扩展位，即对于n位的CORDIC运算，在迭代运算时使用n+m位，在迭代结束后舍弃m位，这样做可以保证前面的n位不受到截断误差的影响.。本文选取了18位CORDIC来说明扩展位和迭代次数对精度的影响。对于圆坐标旋转模式，输入向量为x=2.0，y=0.0，z∈[-π，π]的所有可能输入向量；对于圆坐标向量模式，输入为模为2.0，夹角属于[-π，π]的所有可能输入向量；对于双曲旋转模式，输入为 x=2.0，y=0.0，z∈[-1.0，1.0]的所有可能输入向量；对于双曲向量模式，输入为 x=a+1，y=a-1，α∈[0.25，1.0]的所有可能输入。各个函数的误差与所选取的迭代次数和扩展位的关系如表4所示。

表4 几种配置下的各函数的计算误差，单位为ulpTab.4 Error of functions under several configurations

其中ulp为最低位单位。对于20位定点数有1ulp=2-18。配置为扩展位数和迭代次数。通过实验可以发现，对扩展后的向量进行截断会带来显著的误差增长。并且只会在使用较长扩展位时对结果进行舍入才有明显的效果，因为扩展位较少的情况下舍入反而可能会让结果向错误的方向舍入。最后值得注意的是双曲模式下的函数误差高于圆坐标模式，由（8）可知这是由于双曲模式向量角度收敛性更差而导致的。

5 结束语

本文提出的CORDIC协处理器可以容易地集成进目前常见的航天级FPGA中，为CPU提供更强的三角函数和超越函数运算能力。在中端的V4系列FPGA中实现万分之1精度的三角函数和超越函数只需要不到10%的资源，并可运行于较高的系统时钟下。CORDIC协处理器提供了并行运算几种常用三角和超远函数的功能，不仅适用于导航计算机，也可以被用于其他有大量实时性计算需求的嵌入式系统中。

[1]闫捷，徐晓苏，李瑶，等.基于DSP与FPGA的嵌入式组合导航计算机系统设计 [J].测控技术，2013，32（12）:61-64 YAN Jie，XU Xiao-su，LI Yao，et al.Design of embedded integrated navigation system based on DSP and FPGA[J].Measurement&Control Technology，2013，32（12）:61-64.

[2]Texas Instrument.TMS320C54x DSP Library Programmer’s Reference[EB/OL].（2013）.http://www.ti.com.cn/lit/ug/spru518d/spru518d.pdf.

[3]Volder JE.The birth of CORDIC[J].Journal of VLSI Signal Processing Systems，2000，25（2）:101-105.

[4]Walther J S.The story of unified CORDIC[J].Journal of VLSI Signal Processing Systems，2000，25（2）:107-112.

[5]Jean-Michel Muller.Elementary Functions Algorithms and Implementation Second Edition[M].Boston:Birkhäuser，2005.

[6]王思聪，文治平，于立新.空间用CORDIC处理器的结构级设计方法[J].微电子学与计算机，2006，23（8）:57-60.WANG Si-cong，WEN ZHi-ping，YU Li-xin.The architecture desing method of CORDIC processor used in space[J].Microelectronics&Computer，2006，23（8）:57-60.

[7]Munoz DM，Sanchez DF，Llanos CH，et al.FPGA based floating-point library for CORDIC algorithms[A].Programmable Logic Conference （SPL） 2010 VI Southern[C]//Ipojuca，2005:55-60.

[8]Sarbishei O，Radecka K.On the Fixed-Point Accuracy Analysis and Optimization of FFT Units with CORDICMultipliers[A].Computer Arithmetic （ARITH），2011 20th IEEE Symposium[C]//Tubingen，2011:62-69.