基于粒计算的XML近似多值依赖的判定算法

金 花，殷丽凤

（大连交通大学 软件学院，辽宁 大连 116028）

粒计算[1-2]是人工智能领域中的一种新理念和新方法，它覆盖了所有和粒度相关的理论、方法、技术和工具，主要用于对不确定、不精确、不完整信息的处理，对大规模海量数据的挖掘以及对复杂问题的求解。目前，它在粗糙集理论、概念格、知识工程、数据挖掘、人工智能、机器学习等领域有潜在的应用，已成为信息科学的研究热点之一。

XML（eXtensible Markup Language）已经成为 Internet上数据表示和信息交换的标准，由于不确定数据的普遍存在性，研究表示和处理不确定XML数据成为一个新的研究领域。不确定数据[3]包含不完备数据、概率数据以及集值数据，我们[4]已经对不完备XML数据规范化理论进行了研究；很多学者对概率XML数据各种查询处理技术[5-7]进行了研究；目前集值XML数据研究得还很少。本文对确定XML数据进行扩展，允许叶子节点取值为原子值的集合（称作集值XML数据）。分析集值XML数据库模型，给出相似关系，研究集值XML数据中路径间的多值依赖。根据粒计算中的等价粒概念采用位模式描述集值XML数据库，最后给出XML近似多值依赖（记作XAMVD）的判定算法。此理论成果为集值XML数据库的规范化、路径约简和查询问题等方面的进一步研究奠定了基础。

1 基本概念

为了研究近似XML多值依赖，首先给出集值XML数据库模型、集值XML数据库、相似冗余等相关定义。

定义1一个集值XML数据库模型为一棵树，记为Tm，其中 Tm为六元组，即 Tm=（Vm，Em，lab，ele，N，Dom），其中：

1）Vm表示树的节点的集合；Vm=Vms∪Vml∪Vmr， 其中 Vms表示结构信息，即分支节点；Vml表示数据信息，即叶子节点；Vmr代表根节点。

2）Em表示树边的集合；

3）lab表示元素名字（EN）和属性名字（AN）的集合；

4）ele表示从节点Vm到Vm中一系列节点的部分映射，满足对∀∈Vm，ele（v）=[v1，…，vn]且边（v，vi）∈Em，其中 i∈[1，n]；

5）N是从树节点 Vm到 Lab的映射，若任意 v∈VS，则 N（v）∈EN，若任意 v∈Vl，则 N（v）∈AN；

6）Dom为T中所有叶子节点的值域；

定义2同态映射[8]。设XML模式树Tm′和Tm之间的映射函数为 φ：Vm′→Vm，若（Vm′r）=Vmr，则称映射 φ 为根保持的；若∀v′∈Vm′，有 N（v′）=N（φ（v′）），则称映射 φ 为名字保持的；若φ满足下面的两个条件，则称φ在Tm′和Tm之间是同态映射。

1）若 Tm′中任意一条边（v′，w′）∈Am′，则（φ（v′），φ（w′））∈Am；

2）映射φ为根保持和名字保持。

定义3一个集值XML数据库是一个由n棵树组成的集合，记为 TI={T1，T2，…，Tn}=（V，E，lab，ele，N，Dom，Val），其中Ti=（Vi，Ei，lab，ele，N，Dom，Val），Vele，N，Dom的定义与定义1相同，Val为叶子节点的取值，且取值可为非原子值。

集值XML数据库对确定的XML数据库进行了扩展，允许叶子节点的信息值是多个原子值的集合。本文限定TI中任意一棵树与Tm之间都存在同态映射，称TI为Tm的一个实例。T1，T2，…，Tn的信息可以看作是每个对象信息的描述。

定义 4 对于 Ti中的 2个节点 v′，v″∈Vi，如果存在节点集合{v1，v2，…，vn}，使得 v1∈ele（v′），v2∈ele（v1），…，vn∈ele（vn-1），v″∈ele（vn）成立，其中，w0=lab（v′），w1=lab（v1），w2=lab（v2），…，wn=lab（vn），wn+1=lab（v″）。

称w=w0/w1/…/wn+1为一条从w0到wn+1的一条路径；

称v′.v1.….vn.v″为通过路径w的一个路径节点集。用函数last（w）表示通过路径w的一个路径节点集的最后节点。

若w0为根节点，wn+1为叶子节点，则称w为全路径。Path（Tm）表示Tm的所有全路径集合，集值XML数据库模型Tm可以看作Path（Tm）的并集构成的树。

定义5设Tm为一个集值XML数据库模型，集值XML数据库TI为Tm的一个实例，Path（Tm）表示Tm的所有全路径集合 。 ∀p∈Path（Tm），∃Ti，Tj∈TI，若 Val（lasti（p））=Val（lastj（p）），则称 Ti，Tj子树存在信息冗余，记作 Ti|Tm≡Tj|Tm，其中lasti（p）表示在Ti中通过路径p的路径节点集的最后节点。若Val（lasti（p））∩Val（lastj（p））≠ψ，则称 Ti，Tj子树存在信息相似冗余，记作 Ti|Tm≈Tj|Tm。 其中，i∈[1，n]，j∈[1，n]。

2 XML近似多值依赖

若根据相似冗余直接定义XML近似多值依赖 （记作XAMVD），会导致XAMVD的定义条件太宽松。为了克服这个缺陷，下面给出相似关系的定义。

定义 6 相似关系。 设 Tm、TI、Path（Tm）的定义同定义 5，p ∈Path （Tm），Ti，Tj∈TI，Ti|p ≈Tj|p。 设 α =，α∈[0，1]其中 card（ ）表示路径信息值的个数，则称Ti与Tj在路径p上具有α级相似关系，记作 Ti|p≈Tj|p=α。

下面给出XAMVD的定义。定义 7设 Tm、TI、Path （Tm） 的定义同定义 5。 在 Tm上的XAMVD具体表现形式为其中Tm）且 P=且 Q={q1，q2，…，qv}，R=Path（Tm）-（P∪Q）且 R={r1，r2，…，rw}。 如果在 TI中存在两个子树 T1，T2满足 T1|pb≈T2|pb，其中 b∈[1，u]。 则在 TI中必存在子树 T3（T3可以与T1，T2相同）满足如下条件：

1）T3|pb≈T1|pb或 T3|pb≈T2|pb。 其中 b∈[1，u]。

由于子树T1，T2的对称性，一定存在另一个子树T4∈TI满足以下条件：

1）T4|pb≈T2|pb或 T4|pb≈T1|pb。 其中 b[1，u]。

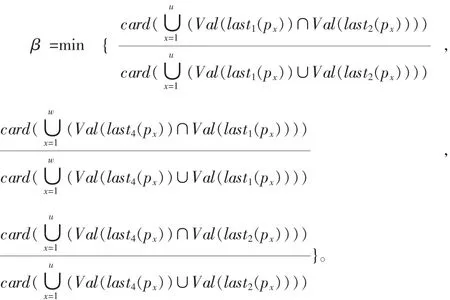
3 XAMVD的判定算法

下面采用粒计算中等价粒的位模式研究XAMVD的判定问题。

定义 8 设 Tm、TI、Path（Tm）的定义同定义 5，p∈Path（Tm），Domp为TI中通过路径p的所有叶子节点的值域，称Domp中语义相同但命名不同的值为一个等价粒，Domp为所有等价粒的并集。|Domp|表示等价粒的个数，设|Domp|=M，路径p的等价粒记为 Domp1，Domp2，···，DompM。

定义 9 设 Tm、TI、Path（Tm）的定义同定义 5，p∈Path（Tm），Ti∈TI={T1，T2， …，Tn}，i∈[1，n]，Ti在 p 上的信息值为 dip={d1，d2，…，df}，其中 dc为原子值，dip为原子值的集合，c∈[1，f]。 Bit为映射函数，Bit：biti1biti2…biti|Domp|， 其映射值为： 当 dc∈Dompj时，bitij=1， 当 dc∉Dompj时，bitij=0。 其中 j∈[1，|Domp|]，c∈[1，f]。

设全路径p对应的值域为Domp被划分为M个等价粒，即有 Domp={Domp1，Domp2，…，DompM}，又设集值 XML 数据库的第i棵子树为Ti，其在全路径p上的信息值记为：dip={d1，d2，…，df}，其中 dc为原子值，dip为原子值的集合，c∈[1，f]。 下面给出dip转换为由M位二进制位串表示的算法。

算法1 Path－Bit－Pattern{求全路径信息值的位模式}

输入：全路径 p，Domp={Domp1，Domp2，…，DompM}，dip={d1，d2，…，df}。

输出：p 在 Ti中的位模式 Bit（dip），1≤i≤n。

Path－Bit－ Pattern（p，Domp，dip）

begin

1）Bit （dip）=00…0；（初始化 dip转换为相应 M 位二进制串，即共有M位0串）

2）for each dh∈dipdo（这里：1≤h≤f）

if dh∈Domprthen（这里：1≤r≤M）

置 Bit（dip）中的第 r位 bitir为 1；

3） return（Bit（dip））；

end.

定理1设TI中子树的个数为n，全路径p对应的信息值的个数最大为m（一般情况下m

证明：算法1的时间复杂度为O（m），求p在TI中的位模式需要调用算法n次，所以求得p在TI中的位模式算法时间复杂度为O（nm）。 证毕。

下面给出利用粒计算的位表示法来检测两个全路径或全路径集之间是否存在XAMVD的算法。

设 Tm为集值 XML 数据库模型，TI={T1，T2，…，Tn}为集值XML 数据库且是 Tm的一个实例，P、Q⊆Path （Tm）。 P={p1，p2，…，pu}，P 在 Ti中的位模式 Bit（Pi）为 Bit（p1i）+Bit（p2i）+…+Bit（pui），Q={q1，q2，…，qv}，Q 在 Ti中的位模式 Bit（Qi）为 Bit（q1i）+Bit（q2i）+…+Bit（qvi），R={r1，r2，…，rw}，R 在 Ti中的位模式 Bit（Ri）为 Bit（q1i）+Bit（q2i）+…+Bit（qwi），其中+表示位的连接运算。

算法2 Determine－XAMVD{XAMVD的判定算法}

输入：全路径集 P、Q、R。

Determine－XAMVD（P，Q，R）

begin

1）flag1=0；flag2=0；

2）利 用 算 法 1 求 出 {Bit（P1），Bit（P2），… ，Bit（Pn）}，{Bit（Q1），Bit（Q2），…，Bit（Qn）}，{Bit（R1），Bit（R2），…，Bit（Rn）}。

3）for i=1 to n－1 do

for j=i+1 to n do

if（αb＞0）then//{其中 b[1，u]}

flag1=flag1+1；

if （βb≥αb≠0） ∨（χb≥αb≠0） then//满 足XAMVD定义的条件1）。

定理2设TI中子树的个数为n，算法2的时间复杂度为O（n2）。

证明：算法2在第2）步求全路径P、Q的位模式的时间复杂度为O（mn）；算法2中第3）步的双重循环时间复杂度为O（n2）；算法 2 的时间复杂度为 O（mn）+O（n2），又因为一般情况下m

采用二进制表示集值XML数据库的多值信息，使得数据格式更接近机器的内部表示，算法的运算效率与速度得到了提高，同时解决了具有相同语义而命名不同的信息值在普通的集合运算下难以区分的问题。

4 实例分析

根据前述所提出的理论，本节给出实例，进行分析。

例5-1下面给出一个描述学校课程安排情况的实例，一门课程可以由多个老师讲授，一门课程可以对应多门教材，也就是说课程与老师之间存在一对多的联系，课程与教材之间也存在一对多的联系。集值XML数据库T存储了课程（course）“数据库”的安排情况，课程“数据库”对应的教材为{数据库系统教程，DB2}、{数据库原理，SQL Server2000}和{数据库原理，DB2，SQL Server2000}，这门课程由{王一，张三}、{王一，张三，李四}和{赵二，李四}讲授。T如图 1所示。

图1 集值XML数据库TFig.1 Set-valued XML database T

由图 1可以看出，T由四棵子树组成， 即 T={T1，T2，T3，T4}。 T的模式由全路径 p，q，r的并集组成， 其中 p=department/course/cname，q =department/course/teacher/tna -me，r=department/course/teacher/text/textname。 各个全路径所对应信息根据语义相同名字不同满足如下等价关系：

department/course/cname:{[数据库]}；

department/course/teacher/tname:{[王一]，[张三]，[赵二]，[李四]}；

department/course/teacher/text/textname:{[数据库系统教程]，[DB2]，[数据库原理]，[SQL Server2000]}；在 T 中全路径所对应的数据信息的位模式如表1所示。

利用算法2判定表 1中p，q，r三者之间的依赖关系，由T1|p≈T2|p=1，存在 T3满足 T3|p≈T2|p=1，T3|q≈T1|q=2/3≤1，T3|r≈T2|r=2/3≤1 成立，存在 T4满足T4|r≈T1|r=1成立，根据XAMVD的定义在T上成立。

表1 全路径信息的位模式表Tab.1 Bit-pattern of full-path information

通过此实例表明信息值采用位表示，在进行XAMVD的判定时，避免了繁杂的字符串比较，提高了算法的效率。

5 结束语

目前，基于粒计算的方法研究不确定XML多值依赖的判定问题，在国内外还处于空白。本文对确定的XML数据进行了扩展，允许叶子节点的信息值是多个原子值的集合。采用粒计算的位模式表示方法研究了XML近似多值依赖的判定问题，根据本方法可以发现潜在未知的XAMVD，信息值采用位模式，一方面使得数据格式更接近机器的内部表示，算法的运算效率与速度得到了提高；另一方面解决了具有相同语义而命名不同的信息值在普通的集合运算下难以区分的问题。

下一步的研究重点主要集中在以下方面：

1）分析集值XML数据库中存在XAMVD引起的数据冗余，提出规范化算法。

2）对集值XML数据的查询进行研究。

[1]Yao Y Y.Paul P.Granular computing:Basic issues and possible solutions[C]//Proceedings of the 5th Joint Conference on Information Sciences.USA：Elsevier Publishing Company，2000:186-189.

[2]王国胤，张清华，胡军.粒计算研究综述[J].智能系统学报，2007，2（6）:8-26.WANG Guo-yin，ZHANG Qing-hua，HU Jun.An overview of granular computing[J].CAAITransactions on Intelligent Systems，2007，2（6）:8-26.

[3]苗守谦，李道国.粗糙集理论、算法与应用[M].北京：清华大学出版社，2008.

[4]殷丽凤，郝忠孝.不完全信息环境下存在XML强多值依赖的XML文档的规范化研究[J].计算机研究与发展，2009，46（7）:1226-1233.YIN Li-feng，HAO Zhong-xiao.Normalization of XML document with strong MVD under incomplete information circumstances[J].Journal of Computer Research and Development，2009，46（7）:1226-1233.

[5]王建卫，郝忠孝.概率XML文件树结点概率的查询算[J].计算机研究与发展，2012，49（4）:785-794.WANG Jian-wei，HAO Zhong-xiao.The query algorithm for probabilistic XML document tree node probability[J].Journal of Computer Research and Development，2012，49 （4）:785-794.

[6]ABITEBOUL S，HUBERT CHAN T-H，KHARLAMOV E.Aggregate queries for discrete and continuous probabilistic XML [C]//The 13th International Conference of Database Theory.Lausanne， Switzerland，2010:50-61.

[7]NING B，LIU C F，YU J X，et al.Matching Top-k answers of twig patterns in probabilistic XML[C]//Database systems for advanced applications， the 15th international conference，Tsukuba， Japan，2010:125-139.

[8]Hartmann S，Link S，Kirchberg M.A subgraph-based approach towards functional dependencies for XML[C]//Seventh World-Multi conference on Systemics，Cybernetics and Informatics， invited Session:Dependencies on the Web，2003:200-205.