基于混合模型的溢流坝参数反演和监控指标拟定
吕高峰,朱锦杰,吴 伟
(国家能源局大坝安全监察中心,浙江杭州,311122)
0 前言
混凝土坝坝体物理力学参数是衡量坝体质量和监控大坝安全运行性态的一项重要指标,是大坝结构计算的重要参数,因此获取大坝当前实际的物理力学参数是分析和评价大坝安全性态的前提和关键。由于施工质量、裂缝以及其他不确定因素的影响,其设计值与实际值存在较大差异,即使是现场采样试验,其结果也只能反映大坝局部情况。而且随着坝龄增长,混凝土发生徐变和老化,混凝土坝的物理力学参数有较大改变。大坝变形是大坝在各种荷载因素作用下的综合效应量,因此采用变形监测资料反演大坝结构整体综合弹性模量是一种有效的方法。笔者基于混合模型反演方法,结合某混凝土溢流坝段坝顶的顺河向位移,通过有限元计算坝顶的位移,温度分量和时效分量采用统计模型,然后与实测值进行优化拟合建立模型,并以此反演坝体混凝土和坝基的弹性模量,并建立监控指标,为评价大坝安全和监控大坝变形提供参考依据。
1 工程概况与测点布置
某水电枢纽工程由挡水、发电、泄洪、通航四大建筑物组成。大坝共分23个坝段,从左至右布置依次为左岸非溢流坝段(1~3号坝段)、电站厂房坝段(4~8号坝段)、深孔泄洪坝段(9~11号坝段)、纵向围堰坝段(12号坝段)、表孔泄洪坝段(13~19号坝段)、升船机坝段(20号坝段)、右岸非溢流坝段(21~23号坝段)。大坝为碾压混凝土重力坝,最大坝高57.00 m,坝顶高程83.00 m,坝顶全长439.50 m。泄水建筑物设有3个孔口尺寸为9.0 m×9.4 m(宽×高)的深孔和6个孔口尺寸为14.0 m×18.0 m(宽×高)的表孔。
大坝共布置4条倒垂线(IP01~IP04)和4条正垂线(PL01~PL04),1条线1个测点,分别布设在6号、9号、12号和19号坝段基础廊道。6号坝段(IP01、PL01)和12号坝段(IP03、PL03)的垂线组用于校测坝基引张线端点的位移。
2 大坝物理力学参数的反演和指标拟定
2.1 混合模型
大坝变形主要受水压、温度及时效的影响,其任一点变形都可以用如下数学模型表示:

式中:δH、δT和δt分别表示水压位移分量、温度位移分量和时效位移分量。
2.1.1 水压分量
在水压作用下,大坝任一观测点产生的顺河向水平位移δH由三部分组成(如图1所示):库水压力作用在坝体上产生的内力使坝体变形而引起的位移δ1H;在地基面上产生的内力使地基变形而引起的位移δ2H;以及库水重力作用使地基面转动所引起的位移δ3H。即:


图1 δH的三个分量 δ1H,δ2H,δ3H示意图Fig.1 Three components ofδH
通过有限元方法就可以知道三个水压分量的位移。在混合模型中,为了简化计算,一般都假定库盆材料参数与基岩参数一致,并且假设计算对象为两种模型:坝体为弹性体、坝基为刚体,以及坝体为刚体、坝基为弹性体。坝体混凝土的弹性模量EC和坝基基岩弹性模量Er采用设计值,在不同水压力作用下,分别算出坝体变形,经曲线拟合,可得拟合曲线:

式中:和分别为两种计算模型下的坝体位移,H为上游水深,ai为拟合系数。
由于计算中采用的弹性模量是设计采用值,与实际有所差异,所以可以用参数X和Y来调整。

将两种计算模型下获得的坝体位移叠加,即得水压位移分量δH。
当调整系数X、Y已知后,由于各自的水压分量δH与坝体弹模Ec和坝基弹模Er成反比,从而可进行坝体弹模反演,反演公式如下:

式中:Ec0和Er0分别为坝体弹模及坝基弹模设计采用值。
根据大坝实际情况,以19号坝段(溢流坝段,坝高51 m,坝底宽41 m,基岩高程29.5~32 m之间)为例建立有限元模型。有限元建模区域包括坝轴线往上游150 m,坝轴线往下游210 m,坝基往下100 m。模型共计16 634个单元,21 134个节点。建模过程中将观测点安排在节点上,有限元计算模型见图2。

图2 19号坝段有限元模型网格划分图Fig.2 Finite element mesh of dam section No.19
计算参数取值来源于《工程专项竣工验收设计报告》,不同部位的混凝土材料不同:泄流面与水接触部位采用抗冲耐磨混凝土,标号为R90350S4;坝体(包括胸墙)采用R90200;基岩材料根据工程前期工作取弹模为15 GPa。具体参数见表1。
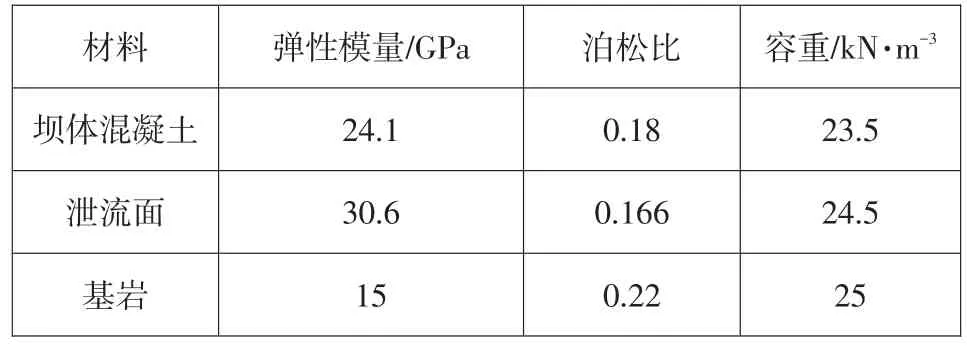
表1 坝体坝基材料参数表Table 1 Parameters of dam foundation material
计算过程中考虑不同的上游水深:上游水位分别取设计水位80 m、校核洪水位82.9 m、死水位78 m,以及75 m、70 m、65 m、60 m和55 m;下游水位波动很小,统一取平均水位42 m。
有限元模型中没有设置闸门,闸门的受力根据蓄水位通过水力学计算方法换算成集中力,直接作用到牛腿位置的18个节点上。蓄水位低于闸门底高程,牛腿不受力。闸门泄洪时,溢流坝段闸门不受力,也就没有水压力通过闸门传递到牛腿,在实际运行中,泄洪时段很少,故不考虑闸门泄洪情况。
通过不同工况(改变上游库水位)的计算,可得上游水位与坝顶水平位移的关系曲线,见图3。由图可知:水压分量与坝顶水平位移呈正相关,因地基变形引起的较大,基本接近的一半。
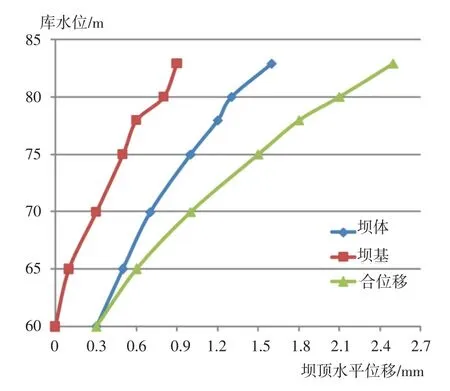
图3 19号坝段坝顶水平位移和库水位的关系曲线Fig.3 Relationship between horizontal displacement of dam crest of section No.19 and reservoir water level
通过计算得到19号坝段垂线测点PL04水压位移的表达式,见表2。

表2 水压位移表达式Table 2 Expression of displacement caused by water pressure
2.1.2 温度分量
温度分量仅次于水压分量,通常情况下,气温升高,坝体往上游变形,气温下降,坝体往下游变形。在运行期,坝体温度取决于外界气温,其坝区气温测值过程线见图4,由图可知,坝址区气温测值基本呈年周期变化。
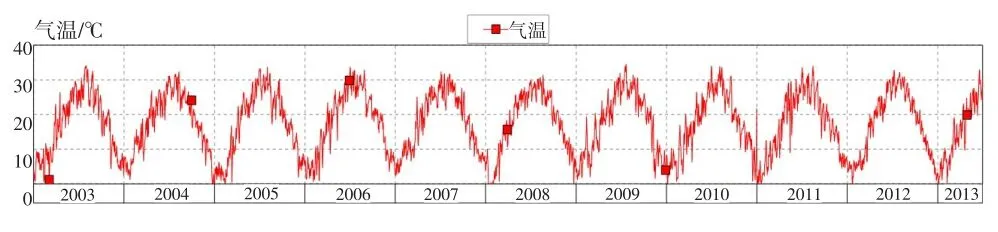
图4 坝址区气温测值过程线Fig.4 Process line of temperature at the dam site
坝体温度变化一般只与表面法向深度X坐标有关,热传导方程可以简化为:

解得:

说明在任何瞬时τ,坝体温度呈波状,周期与气温变化相同;深度X处温度比表面温度落后一个相位角;振幅随深度X的增加而衰减。因此距表面越深,受气温短期波动的影响就越小,而距表面某一深度t时刻的温度只取决于前一定时段内的平均温度。据以上分析,可采用滞后气温作为温度因子,并采用多段平均气温的线性组合,其表达式为如下形式:

2.1.3 时效分量
随着时间的推移而引起的时效位移分量很复杂,与徐变、裂缝的开展、断层带和裂隙的压密等有关。对运行性态正常的大坝来说,时效位移的一般规律是:初期变化快,后期变化慢,最终趋于稳定。据此规律,并结合大坝的实际情况,选取相应的时效因子分别为:t,ln(1+t),。由此,综合水压分量和温度分量,其混合模型表达式为:
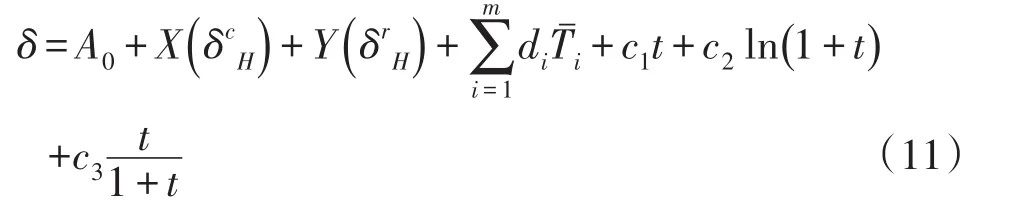
式中:t为时间基准日至观测日的累计天数。
2.2 坝体弹模反演
由2004~2013年间19号坝段正垂PL04测点的观测资料,通过逐步回归计算,求得的混合模型成果见表3。根据表3的拟合系数,可得坝顶水平位移的拟合值,实测值和拟合值过程线见图5。由图表可知:(1)坝顶和坝基的调整参数X和Y分别为0.825 34和0.952 54,小于1。可见,坝体和坝基实际综合弹模比计算值大。由X=Ec0/Ec和Y=Er0/Er可知Ec和Er为29.20 GPa和15.75 GPa。(2)时效分量的系数很小,说明时间对变形影响很小,坝体基本趋于稳定。(3)温度分量的系数较大,尤其是坝顶测点回归方程中温度分量的系数,说明温度分量对坝体水平位移影响很大。(4)复相关系数R为0.892,剩余方差为0.921,实测过程线与拟合过程线基本吻合,实测值与拟合值非常接近,说明该混合模型精度较高,结果可信。
2.3 监控指标拟定
根据上述分析成果,表3中的回归方程可作为19号坝段坝顶的预报模型。预报和监控的原则为:

表3 混合模型回归方程Table 3 Regression equation of hybrid model
(2)2S<|-δ|≤3S时,跟踪观测2~3次,若无趋势性变化,则为正常,否则为异常;
(3)|-δ|>3S时,为异常,应进行成因分析。
式中:δ为实测值,δˉ为混合模型的预报值,S为标准差。
一般情况下,低水位高温季节,向上游的水平位移最大;高水位低温季节,向下游的水平位移最大。从2004年运行至今,根据历史实际水位和温度资料,通过混合模型计算监控指标,计算结果见表4。在不考虑时效因子的情况下,当顺河向位移介于-2.158~8.030 mm之间,测值属于正常;当测值超过这个范围,则要综合其趋势性进行考虑。因时效位移很小,对于以后的测值可简单按表4进行监控。

表4 监控指标统计表Table 4 Statistic of monitoring indicators
3 结语
结合大坝10年左右的坝顶顺河向水平位移实测资料,运用有限元分别计算坝体和坝基引起的水压分量,建立坝顶顺河向水平位移的混合模型,分别反演坝体和坝基的弹模,并拟定监控指标。由计算可知:实测值与拟合值非常接近,说明该模型精度较高、结果可信,反演得到的坝体、坝基弹模和拟定的监控指标符合大坝实际情况。混合模型的水压分量用有限元计算得到,基本上反映了水荷载效应的影响,计算水位包含了多种可能发生的极值,因此混合模型适用于长期预报。
[1]吴中如.水工建筑物安全监控理论及其应用[M].北京:高等教育出版社,2003.
[2]吴中如.混凝土坝安全监控的确定性模型及混合模型[J].水利学报,1989(5):64-70.
[3]卢有清,吴中如.混凝土重力坝变形的混合模型及其应用研究[J].大坝与安全,1989(3):22-34.
[4]沈海尧.混凝土坝位移观测资料分析方法的若干改进[J].大坝与安全,1991(1):47-55.
[5]岳建平,华锡生.坝体弹模及坝基变模反演分析的研究[J].武汉测绘科技大学学报,1993,18(3):82-87.
[6]程琳,徐波,吴波,郑东健.大坝安全监测的混合回归模型研究[J].水电能源科学,2010,28(3):48-50.
[7]张伟,陆桂华,冯威,郑东健.基于ABAQUS有限元分析的大坝变形混合模型[J].水电能源科学,2011,29(6):80-82.
[8]冯威,张伟.基于混合模型的混凝土坝物理力学参数反演分析[J].水电能源科学,2011,29(5):67-69.
[9]邓昌铁,郭震,凌湖南,蒙淑平.上犹江大坝位移混合模型研究[J].河海大学学报,1990,18(7):24-31.
[10]刘成栋,向衍.碗窑水库碾压混凝土重力坝物理力学参数反演分析[J].中国农村水利水电,2009(9):115-117.
[11]包腾飞,郑东健,郭海庆.新安江大坝典型坝段坝顶水平位移监控指标的拟定[J].水利水电技术,2003(3):46-49.

