钢铁采购最优化方案问题的分析

山东职业学院 蔡春花 郑瑞瑞

钢铁采购最优化方案问题的分析

山东职业学院 蔡春花 郑瑞瑞

新经济环境下，市场竞争日趋激烈。销售钢材企业为求生存，提升在市场的竞争能力，必须重视采购分析。本文对某企业销售的各种钢材进行分析，确定采购策略，在钢材需求量已知的条件下，用极大似然估计的方法确定其概率密度函数，求出所研究的各种钢材采购量的上下限。在此基础上，针对多种钢材的采购量建立利润最大化的线性规划模型，求出最优解并作敏感性分析，建模过程中使用了Mathematica软件和Lindo软件。

采购量 极大似然估计 线性规划

钢材企业对利润的追求和规模不断扩大，相应地给钢材管理增加了许多难度。数量就是力量，这是谈判课程中基本的原理。买方的采购批量是买方在谈判中的最大优势，但如何合理运用这个优势却取决于不同的采购战略。对大型钢铁企业来说，采购批量上的优势是相当明显的。此外，运输的时间和成本在钢材采购中的作用也是不可低估的。因此，钢材的采购决策是一个钢材企业取胜的关键。采购分析做充分，整个供应链条就形成了，在稳定的市场环境中就能正常运行。如果市场发生变化，供应紧张时，供应断链的情况就可能发生。这时首先要做的事就是提前备料。采购分析就是要及时了解市场信息，把握市场的供需状态，做好供应工作，同时采购分析也是降低采购成本和生产成本不可缺少的重要环节。影响钢材采购的主要因素有当前可使用的资金、当前可使用的库存、钢材的销量情况、钢材价格、运输因素以及经营风险。其中，库存量与钢材的销量密切相关，必须根据销量正确预测钢铁价格，当预测钢材的价格上升时增加采购数量；当预测钢材的价格下降时及时减少采购数量。参考单种钢材采购方案，分析多种钢材的最优采购方案。

一、模型假设

据以上讨论，可以将决策问题转化为钢材库存、需求和采购资金等约束条件下，为获得最大利润L而求解当前各类钢材需要购买量Di的规划问题。

假设如下：

（1）cli为当前第i种钢材的单位价格，i=A,B,C ;

（2）Ii为当前第i种钢材的实际库存， i=A,B,C;

（3）ui为当前第i种钢材的需要决策采购的数量，i=A,B,C；

（4）Mi为当前第i种钢材的平均利润，i=A,B,C；

（5）si为当前第i种钢材的需求下限，Si为当前第i种钢材的需求上限， i=A,B,C；

（6）K为能够获得的总资金K=8亿。

二、模型建立

需要决策根据以上假设建立如下的决策模型：

可以看出，模型的实质是一个线性规划问题。

三、模型求解

我们针对某钢材企业的实际情况，建立了一个钢材设备采购决策的实例模型。

1.钢材企业基本情况

某钢材企业有钢材企业有四种钢材:钢材A、钢材B、钢材C。

用Matlab可求三种钢材的平均数和标准差，分别为其直方图见表3、表4、表5：

表3 钢材A

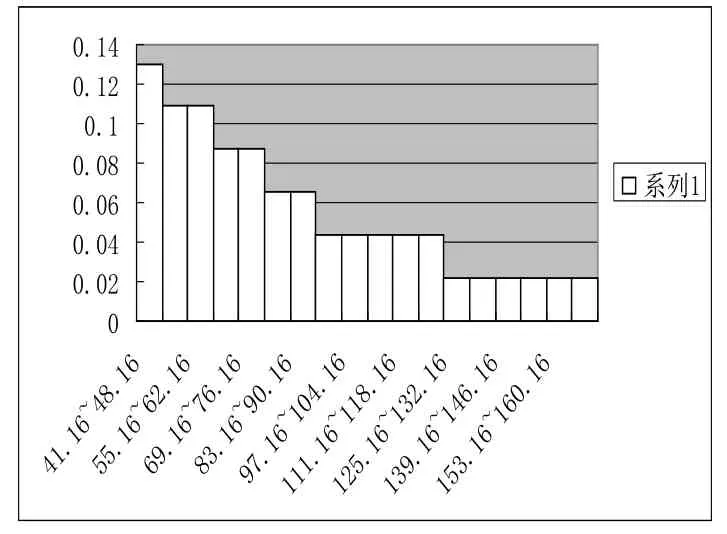
表4 钢材B

表5 钢材C

对上述图像分析可知：钢材A和 C钢材服从正态分布，钢材B大致服从指数分布。由极大似然估计知三种钢材的参数估计，因此三种钢材的概率密度函数分别为：

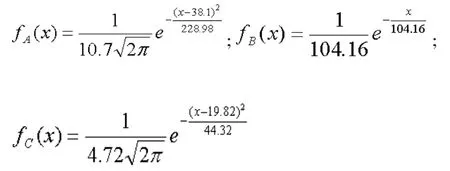
1.各类钢材的需求上限和需求下限

（1）对钢材A来说,设备单价为3200元，单位设备的储存费用为18元，单位设备的缺货费为3600元，c3A即单位钢材出售价格

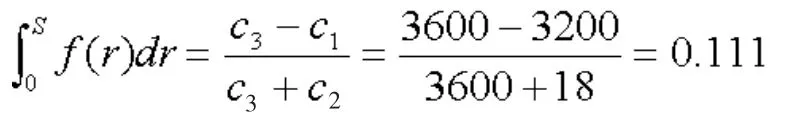
（2）对钢材B来说,位设备单价为3100元，单位设备的储存费用为18元，单位设备的缺货费为3500元，c3B即单位钢材出售价格

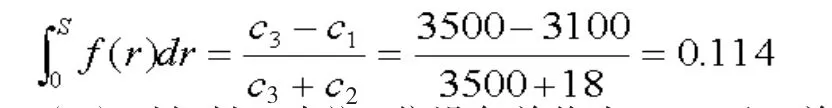
（3）对钢材C来说,位设备单价为3300元，单位设备的储存费用为18元，单位设备的缺货费为3400元，c3C即单位钢材出售价格

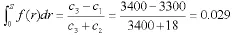
通过Mathematica程序可求得钢材需求的上下限。

2.对模型进行求解

利用Lindo 软件可以很方便的求得本模型的最优解并作敏感性分析，输出结果知：最优解为(66825,108500,75700)

通过上述研究得知，三种钢材的采购方案(66825,108500,75700)按比例采购时，企业所获利润最大。

因此当某种钢材实际库存量小于需求量下限时，则可对该钢材进行采购决策。先对单种钢材进行分析确定采购量及存储策略中的上下限，然后再对三种钢材分析。在已知条件下，用极大似然估计的方法求出三种钢材的概率密度函数，使用Mathematica做数值计算求出三种钢材采购量的上限和下限，并利用Lindo 软件求得多种钢材模型的最优解并作敏感性分析。确定出三种钢材的采购量，使企业的效益最大化。

[1]中山大学统计科学系．概率论与数理统计[M]．北京:高等教育出版社，2004．07

[2]运筹学教材编写组．运筹学（第三版）[M]．北京:清华大学出版社，2005．06

[3]姜启源，谢金星，叶 俊．数学模型（第三版）[M]．北京:高等教育出版社，2003．08

[4]楼顺天，姚若玉，沈俊霞．MATLAB 7．X程序设计语言（第二版）[M]．西安:西安电子科技大学出版社，2006

ISSN2095-6711/Z01-2015-08-0228