基于视觉纹理度的WBCT岩心图像压缩

唐国维 吴 双

(东北石油大学计算机与信息技术学院，黑龙江 大庆 163318)

在推测沉积环境和岩性的研究中，岩心图像起着至关重要的作用。由于岩心图像的采集数据量巨大，因此在岩心图像存储和传输的过程中，需要对其进行压缩处理。通过选取大量岩心图像对其进行实验分析，发现岩心图像普遍存在丰富的纹理特征。针对岩心图像的这种特点，笔者引入图像纹理度(ITM)的概念，通过计算岩心图像经变换后所得系数的图像纹理度，来确定不同纹理区域的最优分解数目，进而作为方向分解数目的依据，可以有效改善压缩效果。目前通常单纯采用传统的图像压缩算法对岩心图像进行压缩，得到的压缩比较低，压缩后的岩心图像较模糊，不利于人眼观察和进一步的岩性分析。为了得到更好的压缩效果，方便人眼观察，根据人眼视觉特性，保留人眼敏感信息，对不同区域进行相应的视觉加权，达到视觉最优效果，压缩后的图像失真度明显下降，对岩心图像的分析研究也更有帮助。

近年来，对岩心图像的压缩编码常采用小波变换，虽能在一定程度上为一维分段平滑信号提供有效的表示[1]，但小波变换只能反映零维奇异信号，不能有效地表达出曲线奇异性，图像的方向、轮廓及纹理信息等特性。为了更好地完善小波方向性的问题，特别是实现多变量函数的二维图像信号最稀疏的表示，在小波变换的基础上，提出了一系列具有多尺度、多分辨率分析思想的变换工具——多尺度几何分析(Multiscale Geometric Analysis，MGA)[2]。其中以Contourlet变换为代表，可以从不同的方向上进行不同程度的临界采样，并以二维形式表达图像，来更好地刻画图像的轮廓和纹理。但是Contourlet变换仍有缺陷，它所使用的普拉斯塔式分解具有4/3的冗余度，导致变换系数严重增加，因此不适用于图像压缩。为解决过度的冗余问题，Eslami R和Radha H提出了小波-Contourlet变换(Wavelet Based Contourlet Transform，WBCT)，能较完善地保留图像的边缘及纹理等重要特征，更适用于存在大量纹理特征的岩心图像[3]。

在此，笔者针对岩心纹理丰富的特点，提出一种基于人眼视觉和图像纹理度，并结合WBCT与SPECK编码的算法，来对岩心图像进行编码压缩。实验发现，笔者提出的算法能更好地保存图像纹理信息，压缩后的岩心图像效果明显改善，峰值信噪比PSNR值也明显提高。

1 WBCT变换①

WBCT变换摒弃了原有的引入数据冗余的LP滤波器，而采用二维小波变换来替代，构建了完全重构且无冗余的滤波器组。通过这样的方法，可以更有效地逼近包含轮廓的图像。WBCT变换分为以下两个步骤：

a. 利用小波变换代替LP变换，采用可分离滤波器，对图像实现多尺度子带分解。

b. 经小波变换后，再利用方向滤波器组分解高频子带。

图1为WBCT原理示意图。

图1 WBCT原理示意图

2 基于视觉纹理度的WBCT对岩心图像压缩编码

2.1 基于人眼视觉特性的加权处理

实验发现，在平滑区域、纹理区域和边缘区域内，人眼的敏感程度不同，因此可以通过对相应区域内的变换系数进行相应的视觉加权，保留人眼视觉相对敏感的信息，提高重构图像的视觉质量。其中，Mannos视觉模型比较成功，应用广泛，其提出的对比敏感度函数(Contrast Sensitivity Function，CSF)是一种频率函数，并且有各向异性的特征，能够较全面又有效地描述人眼对空间频率的敏感性。Miloslavski等提出一种常用的CSF表达式：

CSF(f)=2.6×(0.192+0.114f)e-(0.114f)1.1

(1)

其中，f为空间频率，取值范围为0.0～0.5。根据Kim J等的计算[4]，对不同子块内变换后得到的小波系数分别进行加权，并得到对应的视觉加权系数，见表1。

表1 小波系数的视觉加权

2.2 图像纹理度

自然图像具有明显不同的轮廓和纹理，其所具有的纹理度也是不同的，因此用纹理度来衡量一幅图像也是对图像压缩编码的方向之一。文献[5]中引入平滑度的概念，由于岩心图像纹理丰富，若对纹理信息较少、较平滑的图像区域进行多方向分解，反而会影响压缩效果。因此笔者在平滑度基础上进行改进，提出图像纹理度这一概念，同以往提出的纹理度相比较，更能明显区别岩心图像的纹理度，利用高频子带的纹理度对其进行最优分解，实现最佳的编码效果。

类似于平滑度，衡量纹理度时，首先对分解变换后得到的系数矩阵C(M×N)(M、N分别为矩阵行、列数)归一化得到矩阵C′(i,j)。对矩阵C′，定义以(i,j)为中心，3×3大小窗口范围内的像素为(i,j)的邻域S，当前像素与其邻域内像素均值之差X(i,j)为：

(2)

文献[5]中使用变量X的方差作为标准，然而由于方差是以均值为中心，若抛弃均值本身的影响，所得出的系数偏离程度将更精确，信息量更大，更能反映出当前数值偏离均值的剧烈程度，因此笔者采用变量X的变异系数来反映当前系数的偏离程度，作为图像纹理度(ITM)的标准：

(3)

ITM越大，其图像的纹理性就越强，对应系数偏离均值就越大。通过大量实验，笔者设定以ITM=-0.2为界，这时编码效果最好。

以3种不同的岩心图像(图2)为例分别计算其各个高频子带的纹理度，结果见表2。

图2 3幅岩心图像

表2 3幅岩心图像纹理度

首先对最高层高频子带进行判断，若ITM≥-0.2，则认为图像纹理度高，对其进行四方向分解，否则不进行处理；再对次高层高频子带判断，若ITM≥-0.2或同方向的低频子带进行了四方向分解，就对其四方向分解，否则不处理；最后依照以下方法依次判断同方向高频子带，依此类推，直至最后一层高频子带：

a. 若ITM≥-0.2且同方向低频子带未进行方向分解，对该子带进行四方向分解；

b. 若ITM≥-0.2且同方向上低频子带进行的方向分解数目为n，则该子带的方向分解数目为2n；

c. 若ITM<-0.2，则其分解数目与前一级相同。

以512×512岩心图像3(图2c)为例将岩心图像进行5级分解，最后可得15个子带对应的纹理度，根据该纹理度确定各个高频子带分解方向数目，结果见表3。

表3 岩心图像3的子带分解数目

2.3 岩心图像的小波分解与方向分解

笔者改进的算法首先对变换分解后的岩心图像小波系数按照表1给出的视觉权值进行加权，得到新的系数再对其计算纹理度，根据所得到的纹理度对高频子带图像按照2.2节中给出的分解方法进行相应方向数目的分解。岩心图像的主要分解过程：首先进行小波分解，为了得到更好的压缩效果，利用Daubechies9/7小波对岩心图像进行5级分解；然后对子带进行方向滤波。

通过实验可知，纹理丰富的岩心图像利用小波分解后得到的子代也含有丰富的纹理。根据笔者改进的算法，以岩心图像3(图2c)为例，对其进行5级分解得到的WBCT变换如图3所示。

3 SPECK编码算法过程

变换后的岩心图像通过视觉加权与纹理度优化分解后得到的子代间出现3种小波系数关系：若父代与子代均未参与分解，则小波系数关系与普通小波相同；若父代和子代均参与分解，则子代分解方向数目为父代方向数目的两倍，如图4a所示；若父代未参与分解，子代参与分解，则子代分解方向数目为父代数目的4倍，如图4b所示。

图3 原始岩心图像和WBCT变换

在WBCT分解后，可以发现各方向的高频子带系数间的相关性增强。而SPECK算法的主要思想就是基于块的集合分裂，利用小波子代的能量集中性和同一后代所产生的多个不重要系数之间的相关性消除块间冗余，使含有纹理信息较多的系数可以先被编码，在嵌入式图像编码算法中体现出计算复杂度低、运行效率高的较好性能，因此可以采用SPECK编码方法对变换分解后的岩心图像进行编码，更有利于岩心图像的压缩。

图4 两种父代与子代关系

4 实验结果与分析

为验证上述算法，对512×512的岩心图像3(图2c)进行仿真并与传统SPECK算法相比较。采用Daubechies9/7小波对岩心图像进行5级分解。表4给出了在不同码率下，岩心图像分别经笔者改进算法与SPECK算法压缩后的峰值信噪比(PSNR)的对比。图5给出了码率为0.25时笔者改进算法与SPECK算法重构图像的效果对比图，可以看出岩心图像经笔者改进算法压缩后的PSNR普遍高于传统的SPECK算法，并且图像的主观质量更好，能够较好地保护岩心图像的纹理细节特征。

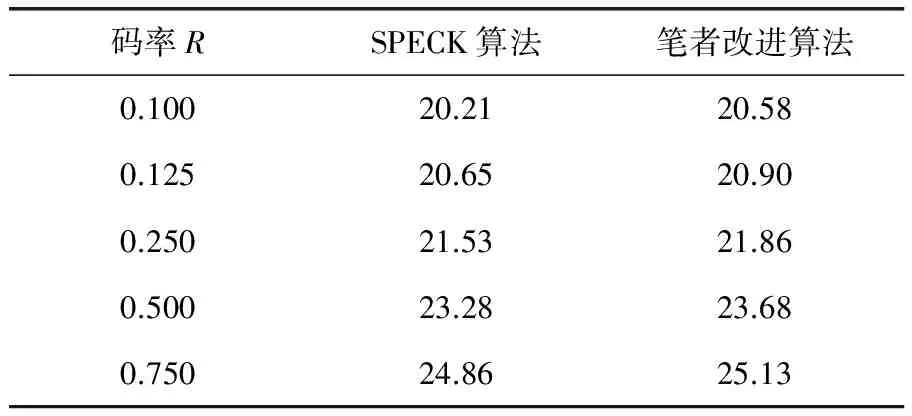
表4 不同码率下的PSNR对比

图5 码率为0.25时的重构图像对比

5 结束语

针对纹理特征丰富的岩心图像，为提高图像的压缩效果，结合WBCT与SPECK编码提出一种基于视觉纹理度的岩心图像压缩算法。这种算法可以根据纹理度确定岩心图像的高频子带最优方向分解数目，为使用SPECK算法对岩心图像压缩编码打好基础。利用该算法对岩心图像压缩后，得到的PSNR值更高，重构后的岩心图像更符合人眼视觉特性，在岩心图像的压缩方向上具有重要意义，对岩心、油藏的研究更加有利。

[1] 陈思，马世红．普通光谱仪用于混色物理实验[J].物理实验，2009，(6)：38～42,46.

[2] Do M N, Vetterli M. The Contourlet Transform:an Efficient Directional Multiresolution Image Representation[J]. IEEE Transactions on Image Processing,2005,14(12):2091～2106.

[3] Eslami R,Radha H.On Low Bit-rate Coding Using the Contourlet Transform[C].Proceedings of Asilomar Conference on Signals,Systems,and Computers.CA,USA：IEEE，2003：1524～1528.

[4] Kim J Y,Kim L S,Hwang S H.An Advanced Contrast Enhancement Using Partially Overlapped Sub-block Histogram Equalization[J].IEEE Transactions on Circuits and Video Technology,2001,11(4):475～484.

[5] 周临川．基于多尺度几何分析的小波变换压缩编码算法研究[D]．济南：山东大学，2011．