基于ATT7022D的智能三相谐波分析仪设计
杨 帅 李众立 李 理
(西南科技大学计算机科学与技术学院,四川 绵阳 621010)
近年来,由于钢铁等金属熔炼企业的发展,化工行业整流设备的增加,大功率晶闸管整流装置及电力电子器件等各种非线性电力电子装置的开发应用,使得公用电网中出现了大量谐波,造成电网信号波形畸变,致使电能质量严重下降,给电网中设备的安全和可靠运行带来了极大的危害。为了保证电网系统的安全、可靠、高效运行,减少谐波含量是一项紧迫而又有效益的任务,为了达到这个目的,必须能方便准确地对电网谐波含量进行测量。
在测量仪器方面,发达国家的发展比较迅速,测量仪器功能齐全、适用范围广,但价格比较昂贵。较好的产品有美国FLUKE公司的F43B及瑞士LEM公司的LEM3PQ等[1]。国内的谐波测量仪器与国外相比还存在着一定的差距,大多数产品谐波检测精度不高,稳定性和在线实时性差。为此笔者提出了一种基于ATT7022D的高精度、低成本谐波分析仪设计方案。
1 智能谐波分析仪设计方案①
该智能谐波分析仪的工作原理是通过ATT7022D实时对电网电压、电流进行采样,并将采样得到的原始数据传送给STM32F103VE进行数据的分析处理,并按照相应的数学模型计算出各项指标值,以得到现场的谐波状况。该谐波分析仪主要由电压互感器、电流互感器、ATT7022D电能计量芯片、STM32F103VE、存储器、LCD显示屏、RS-485及电源等部分组成。系统的总体硬件结构框图如图1所示。
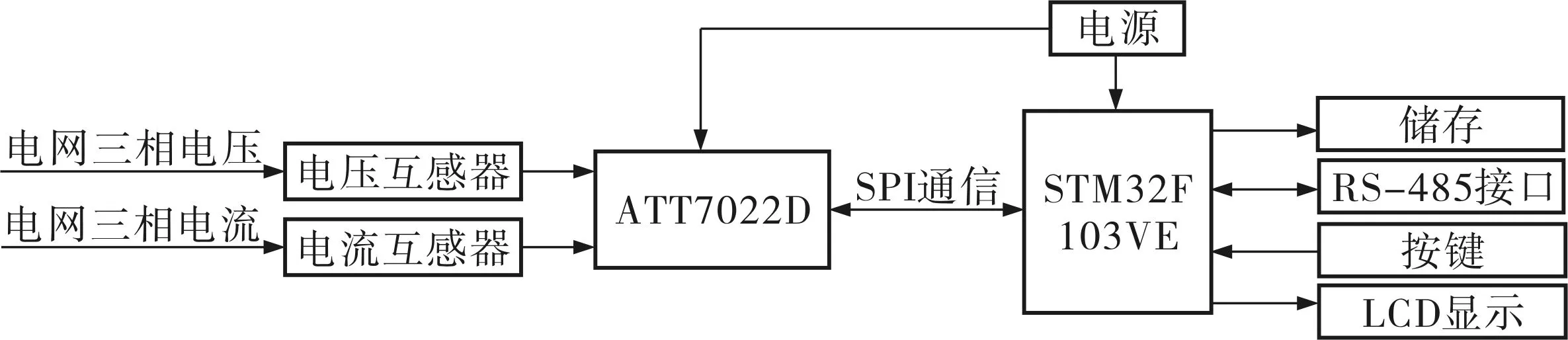
图1 智能谐波分析仪硬件结构框图
2 智能谐波分析仪硬件部分
2.1 电源模块
该仪表将直接接于三相电网中,在电网中只能获得220V或380V电压。由于该仪表中ATT7022D电能计量芯片使用5.0V电压供电,而STM32F103VE使用3.3V电压供电,故设计中增加了220V转12V交流变压器,然后经过整流滤波电路和LM7805、REG1117-3.3稳压芯片分别得到5.0、3.3V直流电压。设计原理如图2所示。
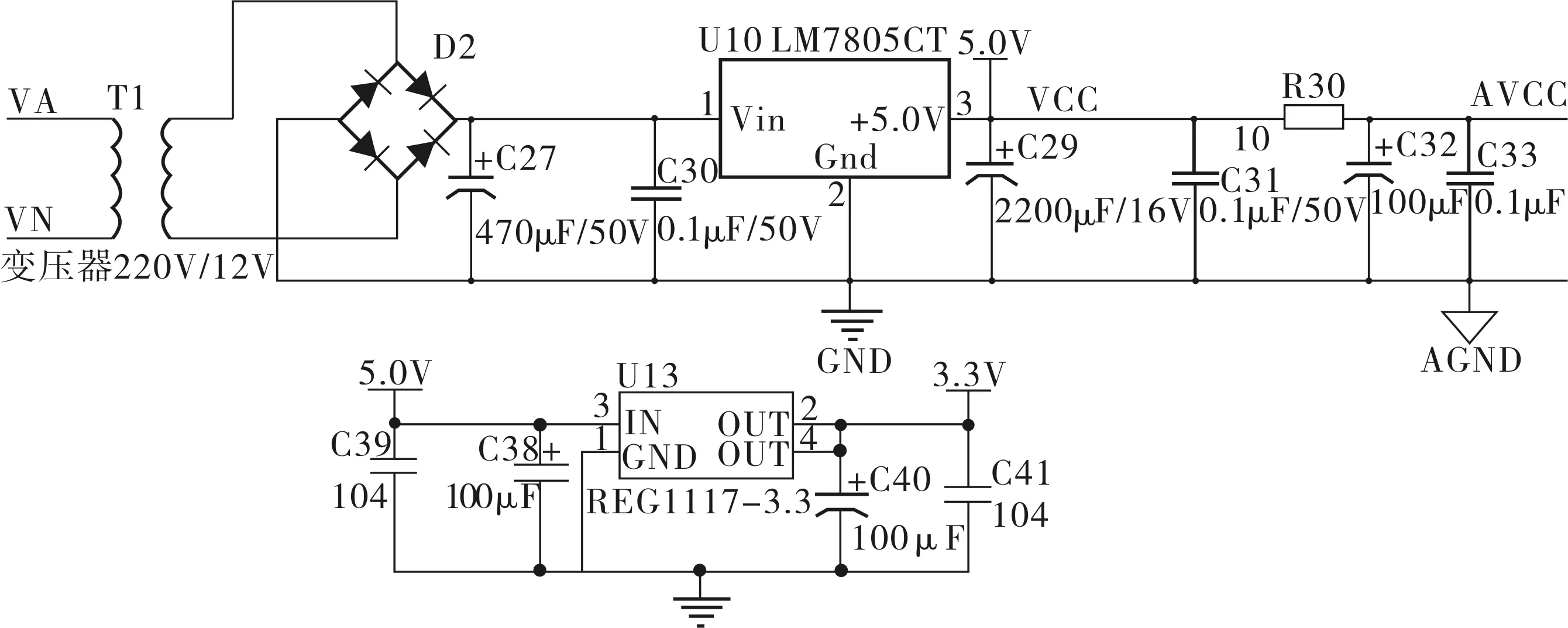
图2 电源电路
2.2 ATT7022D模块
为了实现对电网中电能各个参数的测量,该仪表采用了ATT7022D芯片。该芯片是一款高性能的专用三相电能计量芯片,集成了七路二阶sigma-delta ADC、参考电压电路以及所有功率、能量、有效值、功率因数以及频率测量的数字信号处理等电路[2],它内部还集成了一个240Byte的缓存区,用以实时保存原始采样数据,这些数据可以进一步供用户用做谐波分析和处理。
由于ATT7022D进行电能参数测量时,ADC输入通道最大的正弦信号有效值是1V,所以在与外部电网连接时,要先将电网电压、电流经过电压互感器和电流互感器转换成有效值在1V以内的交流小信号,然后再将转换后的小信号分别接到ATT7022D的电压和电流相应的采样通道中。该仪表采用了TR3121CH型电压互感器和TR2120C型电流互感器(当负载电流过大时可以串联大功率的电流互感器),电压和电流的输入电路如图3所示。

图3 电压、电流模拟输入电路
ATT7022D和STM32F103VE之间是通过SPI总线进行计量参数和校表参数通信的,但由于ATT7022D和STM32F103VE分别采用了不同的工作电压(ATT7022D为5.0V,STM32为3.3V),进行SPI通信时需要进行电平转换,该仪器选用SN74LVC4245——一个8位的双向电平转换芯片进行3.3V与5.0V电平之间的双向转换。ATT7022D与STM32F103VE的SPI通信接口引脚连接如图4所示。
3 谐波采样与分析
3.1 谐波数据采样
对连续电网信号进行频谱分析时,首先要对其进行采样,并且必须要满足采样定理fs≥2fc[3](其中fs为采样频率,fc为信号最高频率)才能得到全部频谱,否则会发生频谱混叠现象。ATT7022D内部集成了一个240Byte的原始采样数据缓存区,采样频率为3.2kHz,完全满足对电网中的30次以内的谐波进行测量要求。该仪表从数据采样到FFT的流程如图5所示,其具体步骤如下:
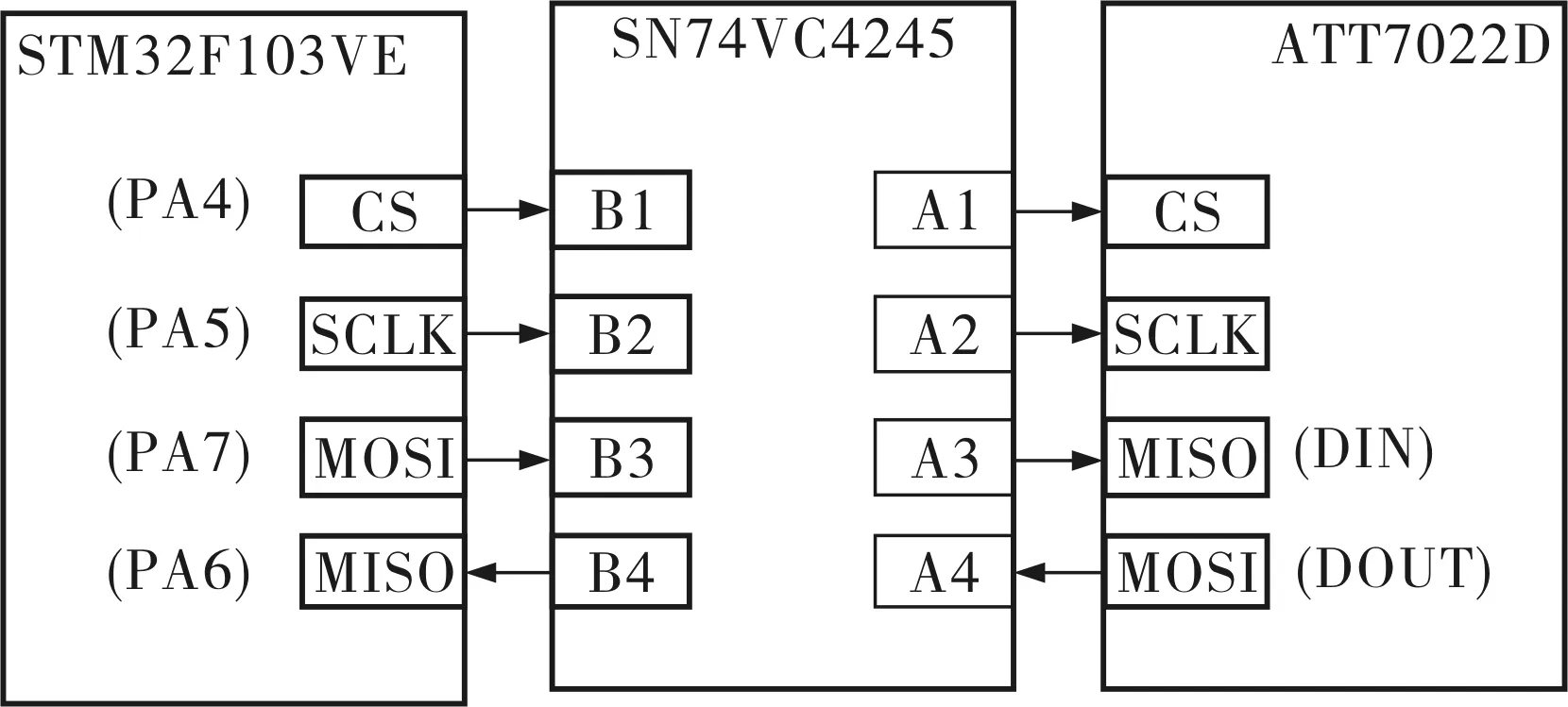
图4 STM32F103VE与ATT7022D的SPI接口连接
a. 开启三通道电压或电流的同步采样功能。发送0xC0命令,写入数据0xCCCCCY,这里Y代表需要保存数据的通道号,0~0x0B有效。
b. 等待采样数据完成。通过读取0x7E指令,判断内部写指针的值,等于240时,表示一次操作完成。
c. 读取采样数据。发送读命令0xC1,读取电压或电流有效值寄存器的值和频率寄存器的值。
d. 对数据进行预处理。采样数据为原始的ADC数据,未做offset校正和增益校正。增益校正时,系数与有效值的校正系数一致。
e. 利用拉格朗日三次插值对采样得到的数据进行插值处理。
f. 将插值处理后生成的新的采样点作为输入量进行FFT变换。
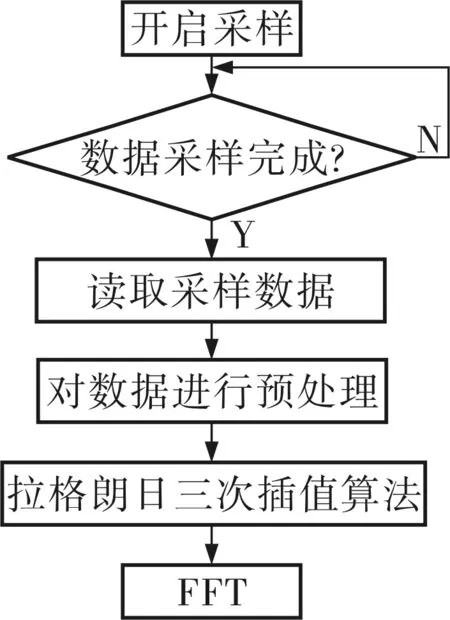
图5 从数据采样到FFT的流程
3.2 谐波分析
通常谐波分析的算法都是采用FFT算法,但在实际电网中由于基波频率的波动,很难保证采样同步,这样会发生栅栏效应和频谱泄漏,很难准确测定各谐波分量。在很多文献里介绍了采用各种窗函数对采样信号进行处理,但由于在对时域连续的信号进行采样时,所处理的离散信号是无限的,如果输入的信号是平稳的(幅度变化不大,也不存在陡变),可采用加窗函数来对信号进行处理,不过加窗函数算法相对复杂,对处理器的处理速度要求比较高,可能会影响到谐波检测的实时性。在实际电网中由于电能信号的波动性,加窗效果并不太理想[4]。该智能谐波分析仪在对采样数据处理时引入了拉格朗日三次插值算法对测得的采样值进行处理,再对处理得到的数据运用改进型快速傅里叶变换进行分析,这样不但简化了谐波的分析过程,克服了因频率漂移造成数据点采样不足的问题,同时也克服了TsN≠T的泄漏问题。
拉格朗日插值算法的数学定义为:对实践中的某个物理量进行观测,在若干个不同之处得到相应的观测值,拉格朗日插值法可以找到一个多项式,其恰好在各个观测的点取到观测到的值,这样的多项式称为拉格朗日插值多项式[5]。从数学上来说,拉格朗日插值法可以给出一个恰好穿过二维平面上若干个已知点的多项式函数,可以利用拉格朗日多项式在一组相关数据中得到更加趋近于正弦曲线的值。
通过ATT7022D可以采集到离散的电压、电流时间序列{u(t)}和{i(t)},该仪表取采样点数N=128。在做FFT谐波分析之前,假设由于频率发生漂移一个整周期刚好采集127个数据,要实现128个点的插值,得到以整数倍于采样频率的等间隔输出。选4个相邻时刻(ti,ti+1,ti+2,ti+3)的采样点数据,然后利用拉格朗日四点三次插值公式进行插值运算:
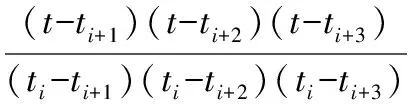
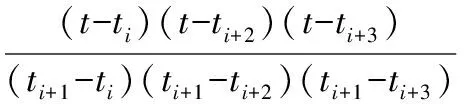
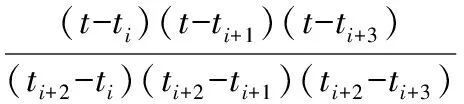
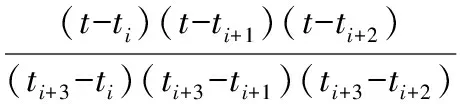
Li+3(t)=li(t)u(ti)+li+1(t)u(ti+1)+
li+2(t)u(ti+2)+li+3(t)u(t3)
通过对原始采样数据进行拉格朗日插值算法处理,可以精确地估算出实际采样时刻的时间序列,然后根据新数值序列,进行快速傅里叶变换,求得其频谱。
4 软件部分
系统软件设计是基于Keil公司开发的集成开发环境RVMDK3.80A,该集成开发环境支持ARM7、ARM9和最新的Cortex-M3核处理器,并且具有强大的simulation设备模拟功能,能对STM32进行指令级的仿真和实时数据分析。本系统主要采用C语言编程,使系统达到较高的精确度并具有较高的速度。软件部分主要由主程序、SPI读写程序、拉格朗日插值程序、FFT程序、显示程序、按键程序、存储程序及RS-485通信程序等组成。系统主程序流程如图6所示。
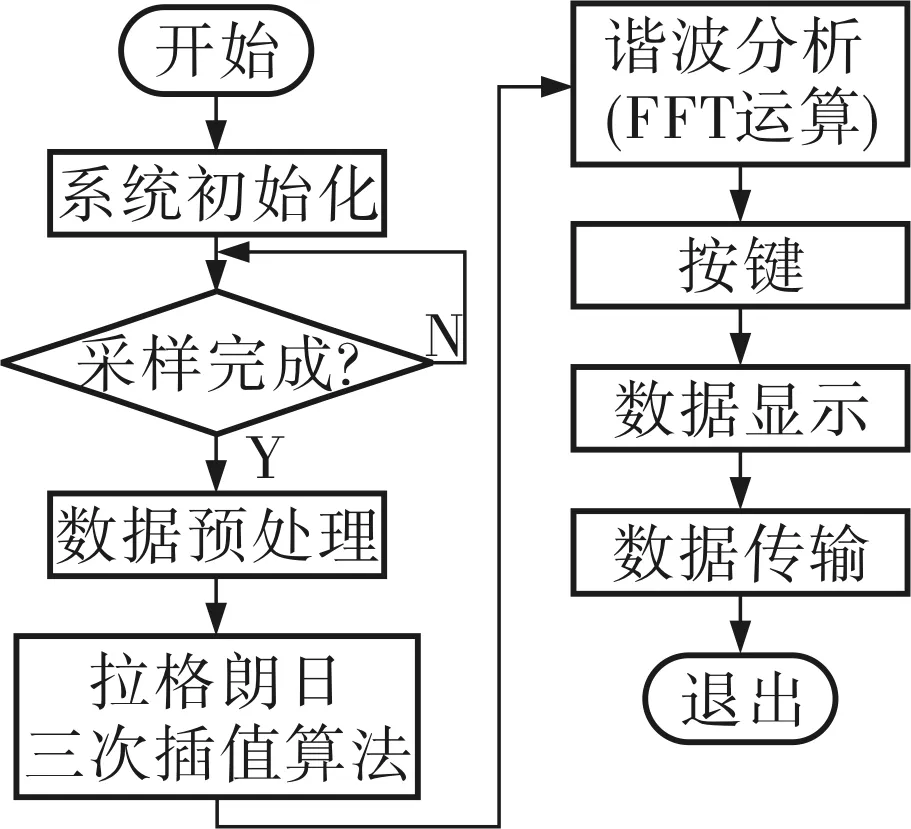
图6 系统主程序流程
FFT是数据处理单元的核心部分,该仪表采用改进的FFT进行数据处理,在采样数据经过拉格朗日三次插值算法修正后,首先对修正后的采样序列进行倒序排列,然后再进行FFT运算,其运算过程如图7所示。
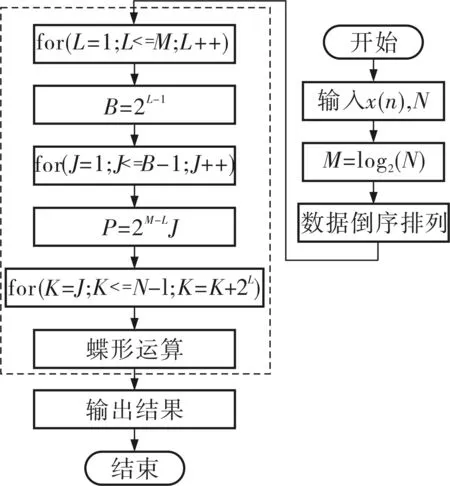
图7 FFT运算流程
5 测量结果与误差分析
5.1 测量结果
为了验证该谐波分析仪的精度,采用输入标准方波对其进行测试,理论表明一个标准方波周期信号可以分解为若干个正弦波的组合。该仪表在测试中先采用美国Fluke公司的6100A电能功率标准源产生电压幅值为100V、频率为50Hz的方波电压信号,然后再用该仪表进行测量,检测结果见表1。
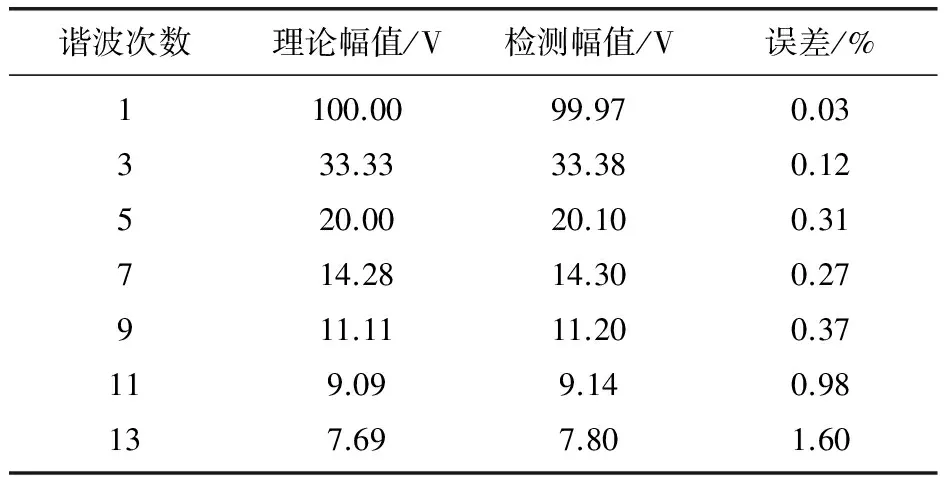
表1 谐波分析仪检测结果
实验结果表明各次谐波测量结果的精度还是很高的,虽然随着谐波次数的增加,谐波测量误差越来越大,但所测谐波数据误差均满足国家标准要求。
5.2 误差分析
电网谐波分析仪的主要误差源有4个方面[6]。
电流互感器和电压互感器的测量精度。为了减小此部分误差,该仪表选用TR3121CH型高精度电压互感器和TR2120C型高精度电流互感器,输入/输出误差均在0.1/0.2以下。
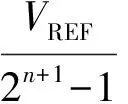
FFT计算的有限精度误差。在处理器STM32F103VE进行FFT运算时,由于算术的有限精度也要引入量化误差,此误差通常可以忽略。
同步误差。同步误差是由电网中采样信号频率波动造成的同步采样偏差,该误差对高次谐波的测量影响非常严重。该仪表在进行FFT运算之前引入拉格朗日三次插值算法对采样数据进行修正,能够有效地克服同步采样偏差,而拉格朗日插值误差主要来自于本身带来的截断误差,该截断误差可以通过拉格朗日插值多项式的余项表达式表示为[7]:
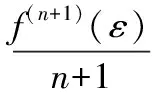
其中ε∈(a,b),Wn+1(x)=(x-x0)(x-x1)…(x-xn)。

由计算结果可以看出,运用该插值算法产生的拉格朗日插值截断误差约为0.000 2,几乎可以忽略不计,能够满足仪表对误差的要求。
6 结束语
根据市场上谐波分析仪存在的不足,以STM32单片机为核心,采用专用高精度电能计量芯片ATT7022D测量电网中各电能参数,并对采样点数据进行拉格朗日三阶插值处理后再进行FFT分析,设计了一款谐波分析仪,实现了对电网谐波的分析功能。经实际使用证明:该设计方案能够对电网中30次以内谐波进行较准确的分析,具有很好的实时性和稳定性,并且成本低,具有很大的市场前景。
[1] 刘艳利.电力系统谐波检测算法研究与实现[D].济南:山东大学,2012.
[2] 张玲,李经章,何伟.基于STM32的防盗电系统设计[J].传感器与微系统,2012,31(4):72~74.
[3] 王茂海,刘会全,彭辉,等.采样信号频率偏离设计值情况下离散傅里叶变换的误差分析[J].电测与仪表,2001,38(1):13~15.
[4] 束慧,陈卫兵.基于ARM和ATT7022C的电能质量监测终端的设计[J].制造业自动化,2012,34(8):34~37.
[5] 徐小丽.拉格朗日插值法在工程应用中的算法实现[J].林区教学,2010,(1):17~19.
[6] 周华,田书林,戴志坚.高精度实时手持式电网谐波分析仪设计方案[J].仪器仪表学报,2005,26(8):290~292.
[7] 汤霖,张艳,李红斌.插值算法在HVDC谐波分析中的应用[J].电测与仪表,2006,43(1):9~11.

