基于灰色系统GM(1,1)模型的短期风速预测算法

靳小钊 王娟娟 赵闻蕾

(大连交通大学电气信息学院，辽宁 大连 116028)

灰色系统理论随着科学学科群和不确定性系统理论的发展应运而生，它是一种针对“少数据”、“贫信息”不确定性系统进行分析的理论，主要通过对“某些已知信息”的探究而得到有利用价值的信息，实现对数据变化规律的正确表达和有效控制，符合系统科学和不确定性系统理论发展的时代潮流，是人类对不确定性系统的认识逐步深化的结果[1]。

目前，风电场风速预测误差在25%～40%之间，这与预测方法有着很大的关系。目前预测方法有很多，如时间序列预测、ARMA模型预测、神经网络模型预测及灰色系统模型预测等[2]。而风速在短时间内，即数据很少的情况下难以发生剧烈变化，正符合灰色系统理论所针对的“少数据”、“贫信息”的应用范围，故在风速的短期预测中，可获得较准确的预测结果[3]。该理论的分析方法主要是根据具体的灰色系统行为特征，充分利用数量不多的数据和信息，寻求相关因素自身与各因素之间的数学关系，即建立相应的数学模型，而GM(1，1)模型是其中最常用、最简单的一种模型。

1.1 原始数据的预处理

设原始数据x(0)=(X(0)(1),X(0)(2),…,X(0)(n))。为了减弱原始数据较强的随机性，在预测中，把原始数据作1-AGO处理，即把数列各项(时刻)数据依次累加，从而得到以下新的数据序列：

x(1)=(x(1)(1),x(1)(2),…,x(1)(n))

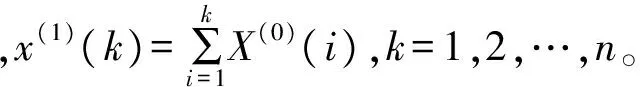
1.2 数据的光滑性检验

一般准光滑序列经过1-AGO处理后，都会减少随机性，呈现出类似于指数变化的增长规律。而原始序列越光滑，对应的1-AGO数据的指数增长规律也越明显。

b.ρ(t)∈(0,ε)，t=3,4，…，n；

c.ε<0.5。

1.3 预测模型的建立

灰色预测模型中GM(1,1)的微分方程为：

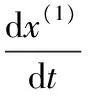
(1)

式中a——发展函数；

u——控制灰数。

GM(1,1)参数列L=[a,u]T的最小二乘估计为：

L=[a,u]T=(BTB)-1BTYN

(2)

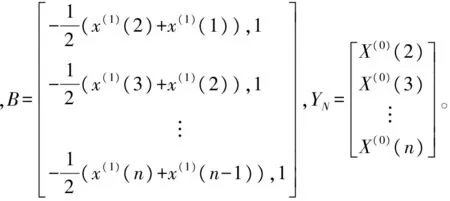
计算得到a、u代入式(1)并解微分方程，令x(1)(0)=X(0)(0),得到以下模型：

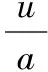
(3)

再做一阶累减还原得x(0),即：

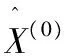
(4)

2 灰色预测模型GM(1,1)应用于风速预测

风速预测与风电场所处地区气候环境、地形地貌及风电装机容量等多种因素有关，这些因素中有些是已知，有些是未知的，具有不确定性和灰色性，因此风速是一个典型的灰色系统。故将该理论应用至风速预测中。

2.1 原始数据的预处理

原始数据为在某风电场所采集的采样间隔为10min的风速数据。X(0)(t)为某日8:00～9:00的风速(m/s)。原始数据及其1-AGO数据序列见表1。

表1 1-AGO风速数据

2.2 对x(0)进行准光滑性检验

2.3 建立模型

根据式(3)、(4)，可得：

YN=[X(0)(2),X(0)(3),X(0)(4),X(0)(5),X(0)(6),X(0)(7)]T

=[1.6500,1.8767,2.4050,3.0767,3.6017,4.1433]T

将a、u代入式(6),得：

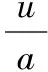
=8.0410e0.1875k-6.5993

2.4 误差分析

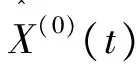
检验结果见表2。

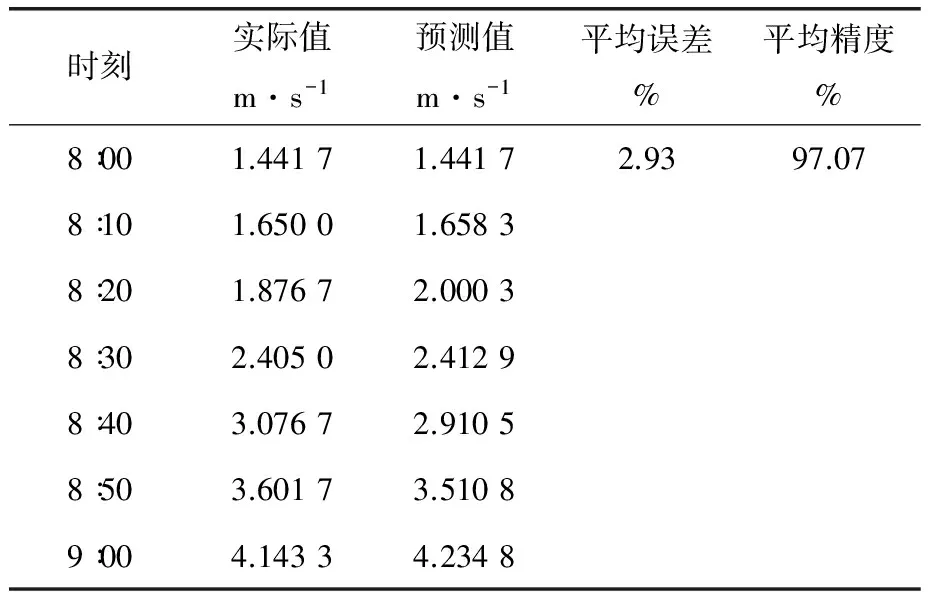
表2 风速动态预测结果

由表2可以看出，用GM(1,1)模型进行风力发电预测，拟合精度高，预测准确，可以进行预测。

根据所建立的预测模型，可得9∶00之后半个小时的预测结果(表3)。

表3 某日9：00之后的风速预测结果

同样测量了风电场在这3点的实时风速，分别为4.560 0、5.080 0、5.693 3m/s，相对误差分别为12%、21%、30%，在风速预测允许误差范围之内。

3 预测结果分析

根据以上预测结果，可以得出：GM(1,1)模型适用于风力发电中关于风速预测的研究；由于原始数据的采样点是递增的，而且预测精度很高，所以通过表3是可以得出未来风速的变化趋势是递增的；随着时间的推移，预测的相对误差逐渐增大，可以推断出这种预测方法只适用于短期的风速预测研究。

4 结束语

在风速预测中，对灰色预测模型GM(1,1)做了试验，其结果在短期内符合实际情况，可应用于短期风速预测，接下来还要通过对风速的预测值进行风电功率预测，从而可以在风力发电中进行电量的提前调度以及其他与风力发电相关的科学研究。但在建立模型的过程中，所取的数据是呈递增趋势的，这对于随机性非常强的风速来说，还应当有更精确的方法进行预测从而减小误差，例如可以剔除之前所取数据，再引入最新测量的数据，继续进行预测。

[1] 刘欣.灰色预测GM(1,1)和GM(2,1)模型的改进研究[D].呼和浩特：内蒙古工业大学,2007.

[2] 王子赟，纪志成.基于灰色-辨识模型的风电功率短期预测[J].电力系统保护与控制，2013，41(12)：79～85.

[3] 李俊芳，张步涵，谢光龙，等.基于灰色模型的风速-风电功率预测研究[J].电力系统保护与控制,2010，38(19):151～159.