基于粒子群优化算法的MP去噪方法优化研究
姚建红 吴 丹 王敏莹
(东北石油大学电气信息工程学院,黑龙江 大庆 163318)
信号去噪在信号处理和故障诊断中占有重要地位。实际测得的信号中都含有噪声,这些噪声的存在严重影响了所得信号的判断结果。因此,如何更好地去掉噪声,提高信噪比,降低均方差,是信号处理的关键。目前有很多去噪方法,如小波阈值去噪法、奇异值分解法及匹配追踪算法(Matching Pursuits,MP)等。其中,小波阈值去噪方法中的阈值很难确定,奇异值分解法中奇异点的位置也容易出现错误,这都增加了去噪的难度。相比之下,MP算法相当于是一种“减去”法,它将信号分解为投影之后得到的系数与原子的线性组合,选择相匹配的时频原子进行信号重构,以此来消噪。然而,该方法所带来的问题就是大量的内积计算,不仅占用计算机内存,而且还不能达到最好的去噪效果。对此,笔者提出利用多目标函数的粒子群算法来进行全局优化,减少计算量。
MP算法一般选择Gabor原子作为时频原子,由其构成算法所需的原子库。根据最大匹配投影原理的策略求得与分解信号最接近的时频原子,经过n次匹配之后,得到一个与原信号最接近的时频原子的线性组合。Gabor原子是4个不同的参数定义的时频原子,它又构成了所需要的过完备原子库,其表达式为:
(1)
Gabor原子库中的原子索引参数r=(s,u,v,ω),变量s、u、v、w依次为尺度、位移、频率和相位。
设f为含有随机噪声的信号,应用MP算法,在经过n次分解后,得到最接近原始信号的信号的步骤如下:
a. 从原子库中选出与f本身最接近的原子gr0,且把f分为两部分,分别是在gr0上的投影分量和剩下的残余分量,表达式为f=〈f,gr0〉gr0+R1f,其中R1f为残余部分。
b. 由于时频原子与无噪的原始信号的内积一定大于其与噪声信号的内积,通过MP算法所得的信号可视为无噪的原始信号。因此,对残差部分进行k次迭代,得Rkf=〈Rkf,grk〉grk+Rk+1f,其中〈Rkf,grk〉为信号或信号残差与原子的内积,即两者的相关系数。
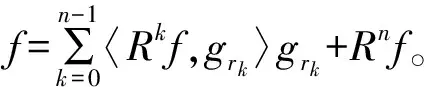
随着迭代次数的增加,与无噪的原始信号相接近的部分越来越明显,每次匹配后的残差越来越少,最后可以收敛为0,这就是MP算法的去噪原理[1,2]。
通过以上步骤,利用MP算法对信号进行去噪,虽然在一些领域上已经取得了一些成就,但是在逐渐研究的过程中,发现其也存在一定的缺点。在迭代过程中,存在大量的内积计算,不仅占用较大内存而且对算法自身也有制约。
2 粒子群优化算法的基本原理
粒子群优化算法(Particle Swarm Optimization,PSO)是由Kennedy J和Eberhart R C提出的一种模拟鸟类觅食行为的寻优搜索算法[3]。粒子群优化算法的基础理论是把鸟类群体中的每个个体比做算法中的单一粒子,而粒子本身要求具有记忆功能,根据自己经验同时也要与其他粒子相沟通、相比较,从而找到最优解。每一个粒子都有一个最佳经验位置,即个体极值pb,整个群体也相对有个最佳经验位置,即全局极值gb。每个粒子都在时刻通过比较这两个极值来改变自身的位置以达到寻求的最优解[4]。假设当前粒子的位置是pi,粒子速度是vi,则最佳位置公式为:
vi=ω·vi+c1·rand()·(pb-pi)+c2·rand()·
(gb-pi)
(2)
pi=pi+vi
(3)
其中ω为惯性权重,随着ω从小到大变化,同时粒子是从局部搜索转变成全局搜索;c1、c2分别反映了个体极值对粒子速度的影响和全局极值对粒子速度的影响;rand()表示(0,1)范围内的随机数。
粒子群优化算法因其自身的特点,在寻找最小值、最优解的问题上取得了一定的成果。而对于前面所说的MP算法去噪时存在大量计算的缺点,可以把信号分解想象成一个粒子寻优的过程[5,6],由此,笔者提出基于PSO的MP去噪优化算法。
3 基于PSO的MP去噪优化算法研究
应用PSO算法最主要是要确定目标函数,即适应度函数。笔者提出采用基于多目标函数的粒子群算法对MP算法进行优化。在MP算法中,最终提取的是最近似于原始信号的有用成分,余下的部分为噪声。只有残差越来越小的时候,同时每次迭代后的最佳原子与上一次信号残差的相关系数的绝对值越来越大才最接近原始信号。所以应用PSO算法寻找最小值,把信号或信号残差与原子两者的相关系数绝对值的倒数和信号残差作为目标函数,即:
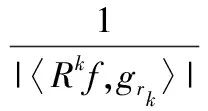
(4)
y2=Rnf
(5)
其中,n≪N。
笔者所提改进算法的实现步骤为:
a. 参数编码。把定义的一个基原子的参数组作为待寻优粒子,就是把要寻找的最匹配时频原子转换到粒子群算法所能处理的搜索空间去进行寻优。
b. 初始化粒子群。初始化粒子的位置和速度,并确定算法的各个参数值。
c. 设定目标函数。笔者采用信号或信号残差与原子两者的相关系数绝对值的倒数y1和信号残差y2这两个函数作为目标函数。
d. 确定寻优标准。分别计算y1和y2的个体极值F1(k)、F2(k),全局极值P1和P2,得出各粒子间的距离dpb=abs(F1(k)-F2(k)),全局最优值的距离dgb=abs(P1-P2)。确定各粒子间的距离dpb为寻优标准。
e. 局部最优位置和全局最优位置的确定。计算全局最优值的距离,用各粒子间的距离与其进行比较,如果优于它,则替换当前位置;反之不变。
f. 更新。根据式(2)、(3)更新粒子的位置和速度。
g. 判断终止条件。若是达到迭代次数或已经得到最优值,则终止;否则返回步骤d。
最终得到需要的时频原子,对原始信号进行重构,去噪结束。
4 仿真实验
为了检验改进方法的去噪效果,笔者对加噪的blocks信号进行去噪仿真实验。先产生纯净信号,信号点数为20,之后叠加信噪比为11.5dB的噪声信号。
取1000个采样点,图1为原始信号,图2为图1叠加含噪信号所得,基础MP去噪结果如图3所示,改进方法去噪结果如图4所示。通过对比图3、4,得出改进方法可以较好地还原原始信号,并且比MP算法能更好地去除尖峰噪声,而且信号更平滑,信号有用成分提取得更多。图5、6分别表示基础MP去噪和改进方法去噪所用的迭代次数,设最大迭代次数为100,对比两图,可知改进方法迭代次数更小,减少了计算量,更快达到了终止条件。
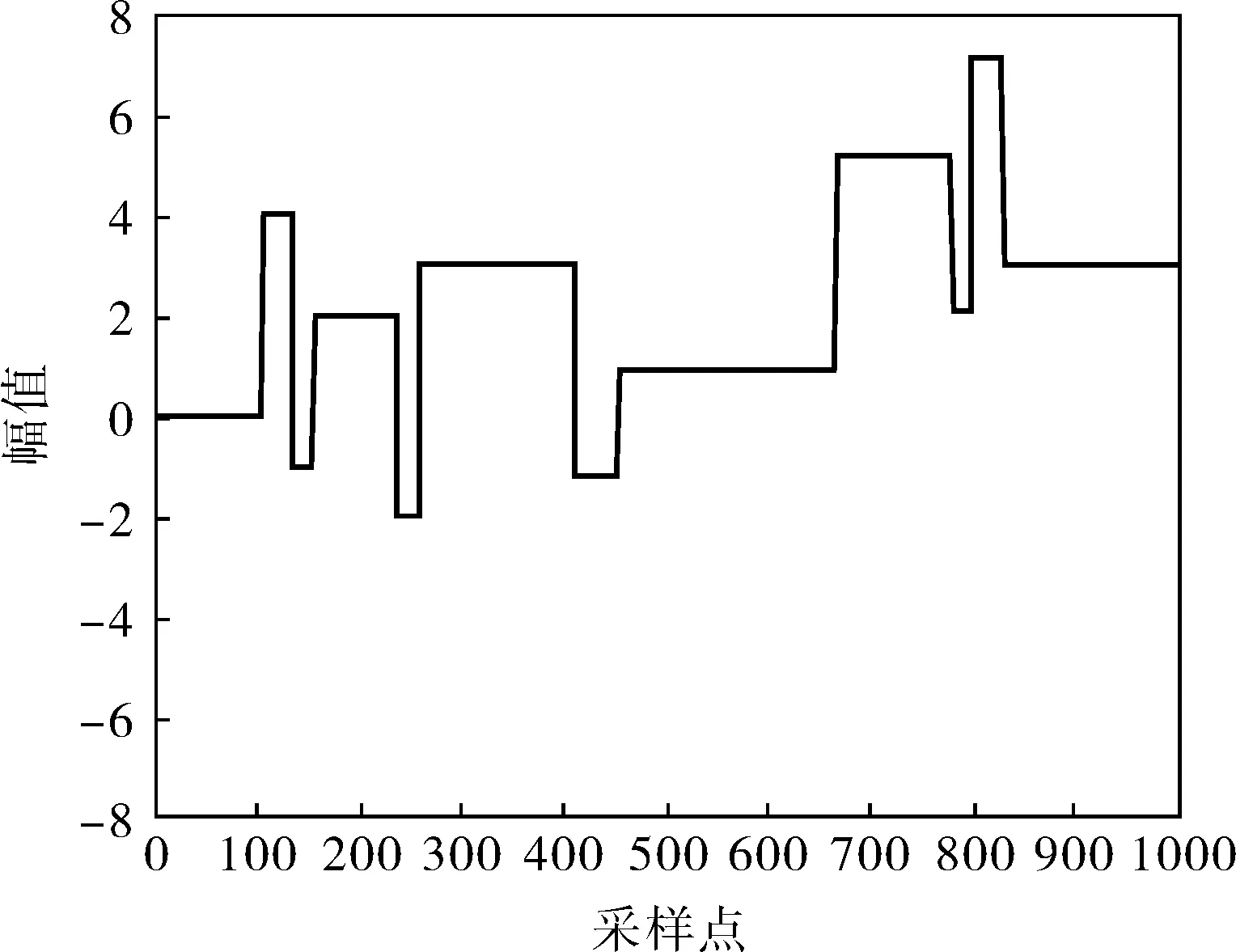
图1 原始信号
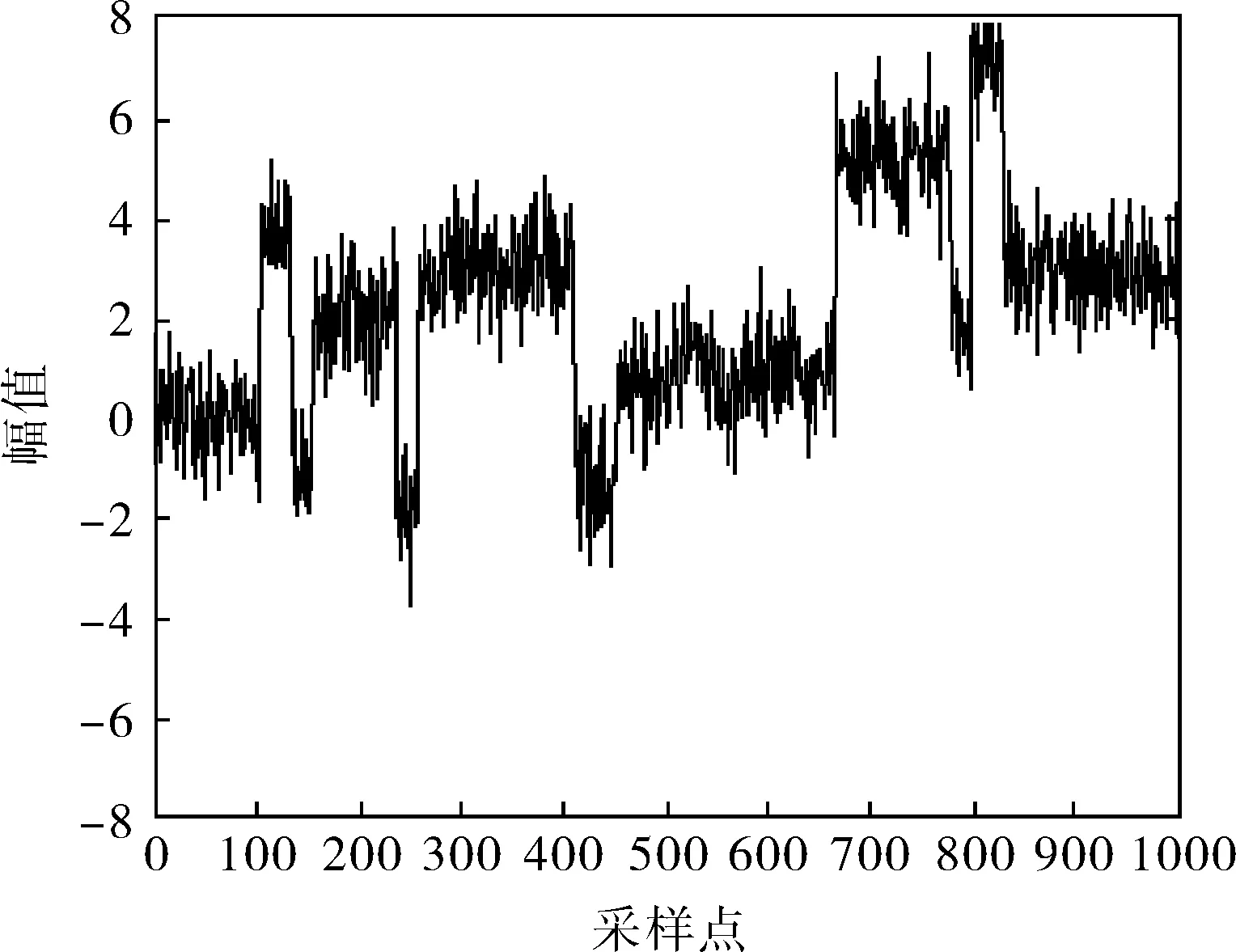
图2 加噪信号
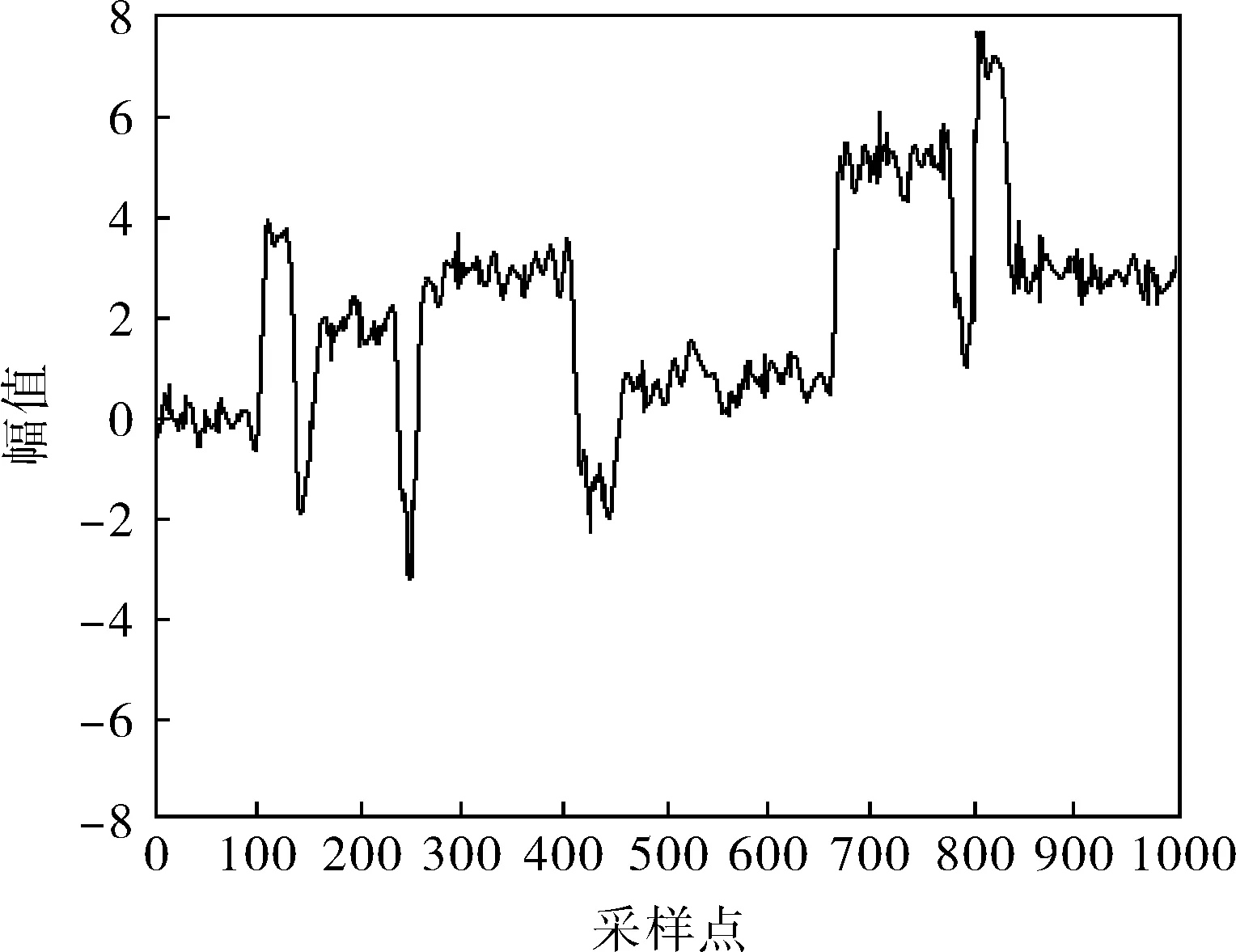
图3 基础MP方法去噪

图4 改进方法去噪
除了通过直观信号的去噪效果图,还可以通过比较信噪比SNR和均方差MSE值来看出改进方法的优越性,信噪比越高说明去噪效果越好,均方差越小说明与原始信号越接近。其算式如下:
(6)
(7)
式中N——信号的长度;
qi——含噪信号;
xi——去噪后的信号。
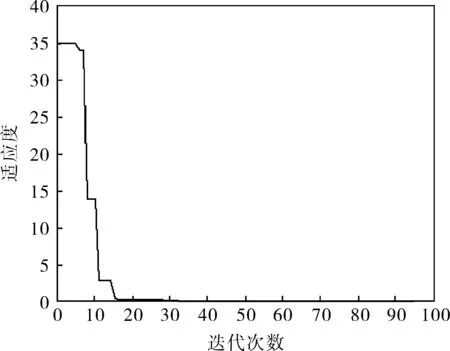
图5 基础MP方法迭代次数

图6 改进方法迭代次数
加噪信号通过两种方法计算的信噪比SNR和均方差MSE结果见表1。
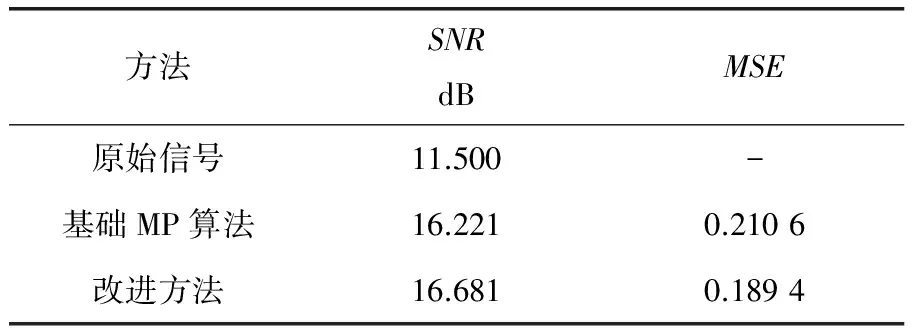
表1 信噪比和均方差对比
通过表1可以看出,改进方法较基础MP算法在这两个指标上都有明显的改善。
5 结束语
笔者应用多目标函数的粒子群算法来优化基础MP算法去噪。对加噪信号进行实验仿真,结果显示:改进算法不仅减少了基础MP算法的计算量,而且得到的去噪信号更趋于原始信号,在信噪比和均方差上更具有优越性。
[1] 陈发宇,尚永生,杨长春.Matching Pursuits方法综述[J].地球物理学进展,2007,22(5):1466~1473.
[2] 邵君.基于MP的信号稀疏分解算法研究[D].成都:西南交通大学,2006.
[3] Kennedy J,Eberhart R C.Particle Swarm Optimization[C].Proceedings of IEEE International Conference on Neural Networks.New York:IEEE,1995:1942~1948.
[4] 黄磊.粒子群优化算法综述[J].机械工程与自动化,2010,(5):197~199.
[5] 王春光,刘金江,孙即祥.基于粒子群优化的稀疏分解最优匹配原子搜索算法[J].国防科技大学学报,2008,30(2):83~87.
[6] 张建军,王仲生,余汇.采用混合粒子群算法实现匹配追踪算法[J].振动与冲击,2010,29(1):143~147.

