Maxwell 阻尼耗能隔震结构平稳响应分析

李创第，陶欣欣，尉霄腾

(1.广西科技大学 土木建筑工程学院，广西 柳州545006;2.广西大学 土木建筑工程学院，广西 南宁530004)

0 引 言

橡胶垫基础隔震结构是一种简单有效的被动控制系统，因具有竖向承载力大、耐久性好、减震效果明显等特点，故在国内外工程设计上得到了广泛应用。国内外大量工程实践表明:橡胶垫隔震技术应用于中低层建筑能够有效减震［1-3］。如:美国(1985)首座采用RSIT 橡胶支座的隔震建筑物，位于距加利福尼亚州断层带20 km 处，在经历了1994 年的加利福尼亚地震后未蒙受损坏;日本神户(1995)凡是装置了橡胶支座的基础隔震建筑物在地震中仅受到轻损坏，采用橡胶支座的桥梁无一倒塌，而其他所有装置了钢铁支座的桥梁却发生断裂;在国内，四川雅安芦山(2013.4.20)地震导致灾区大量房屋损毁，而令人欣慰的是采用隔震橡胶技术的建筑——芦山县医院主楼经受住了强震的考验，主体结构没有出现问题。然而，橡胶垫隔震技术也存在一些不足，其上部主体结构在地震响应中侧移往往较大，这在一定程度上影响了结构的安全性。近二十来年，相关专家学者作了大量研究，并取得丰硕成果。胡智渊［4］研究了基础隔震结构附加粘弹性阻尼器的混合被动控制问题，并推导出了隔震结构混合被动控制的运动微分方程;骆年红等［5］对与位移相关的摩擦型阻尼器用于五层剪切型框架结构的地震响应控制问题进行了系统研究，结果表明，这种与位移相关的摩擦型阻尼器对结构地震响应的控制效果非常显著;吴晶波等［6］对隔震层设置磁流变型阻尼器的智能基础隔震结构半主动控制问题进行了研究;韦捷亮等［7］研究了利用形状记忆合金(Shape Memory Alloy，简称SMA)的超弹性特性设置隔震层支座的基础隔震设计问题，表明隔震层在发生较大水平剪切变形后可通过其支座的超弹性特性恢复到原位并能够保持支座的稳定。橡胶隔震垫本身具有粘弹性质，故本文采用Maxwell 耗能阻尼器模型来模拟橡胶垫的粘弹性质会更加合理，并对此模型进行地震平稳响应分析。

1 结构运动方程

图1 所示为多层基础隔震结构隔震层设置普通Maxwell 阻尼器模型。设上部结构的质量、刚度和阻尼矩阵分别为［M］、［K］、［C］;隔震层的质量、刚度和阻尼分别为m0b、k0b、c0b;x0i、x0b分别为上部结构第i(i=1 ～N)层相对于隔震层以及隔震层相对于地面的位移;P(t)为普通Maxwell 阻尼器提供的阻尼力，则在地震激励x¨g(t)作用下，该结构运动方程为:

图1 结构计算简图Fig.1 Structure calculation diagram

式中:

P(t)为普通Maxwell 阻尼器所提供的阻尼力，P(t)满足［8］:

对于40 m 以下多层规则隔震结构，其上部结构相对于隔震层位移向量{x0}可按第一振型展开，即:

式中，{φs}为第一振型，x1为{φs}对应的广义坐标，{φs}=［φs1φs2… φsi… φsN］T。

将式(4)代入式(1)，结构运动方程(1)可简化为:

式中，ω1、ξ1、r 分别为上部结构第一振型{φs}的频率、阻尼比及振型参与系数，式中

2 结构响应分析

引入状态变量{z(t)}，令其为:

由式(3)和式(5)，可将原结构运动方程组化为如下一阶状态方程组:

式中，

设λj、{Vj}、{Uj}(j=1 ～5)分别为方程(8)的特征根以及左、右特征向量，并令{Vj}、{Uj}为

根据文献［9-12］复模态理论，令:

得结构响应为:

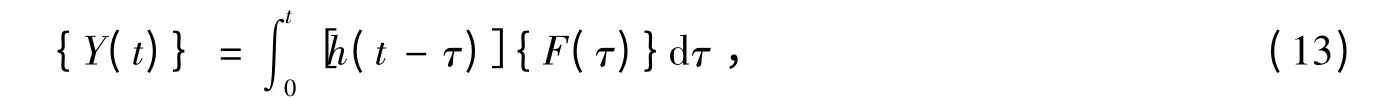
式(13)分量形式为:

式中，{R}=［r η］T。

由式(11)、式(12)以及式(14)，得隔震层相对于地面的位移和速度响应，上部结构相对于隔震层的位移和速度响应，以及阻尼器响应分别为:

3 结构平稳随机响应方差分析

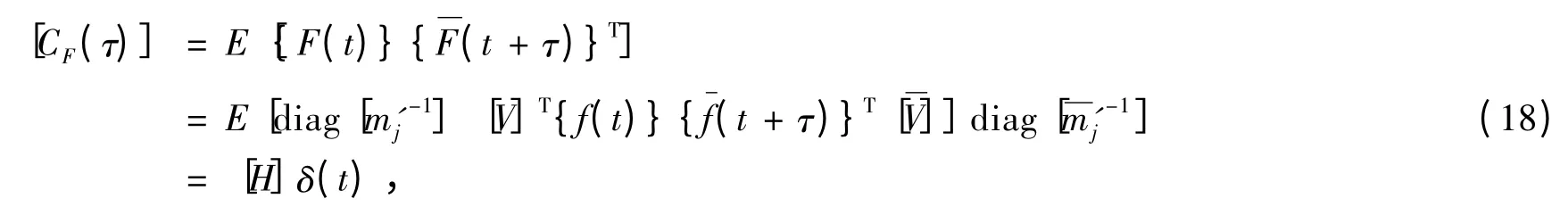
式中，

［H］的分量形式为:

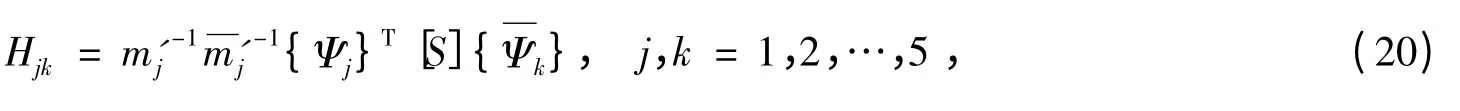
式中，

根据式(13)，模态向量响应{Y}的协方差函数矩阵可表示为:

展开上式得:

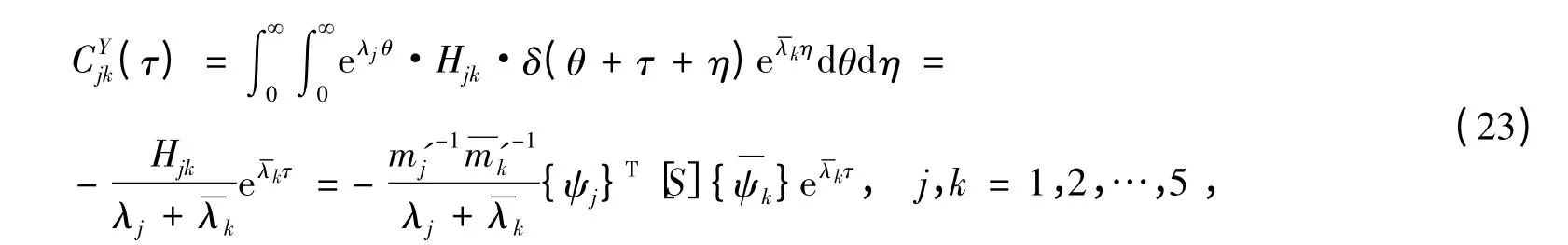
令τ=0，由式(11)、式(12)以及式(23)，得上部结构各层相对于隔震层和隔震层相对于地面的位移、速度响应方差以及阻尼器响应方差精确解:

4 数值算例

某三层附加普通Maxwell 型粘弹性阻尼器基础隔震框架结构建在抗震设防烈度I=8 度(0.2 g)的土地上。隔震结构物及隔震层各层参数为:上部3 层质量m01、m02、m03分别为27、27、18 t;刚度k01、k02、k03分别为24.5、19.6、9.8 MN/m;第一振型系数φs1、φs2、φs3分别为0.333、0.666、1.000。仅考虑上部主体结构受第一振型影响，结构第一振型自振频率ω1=13.47 s-1，阻尼比ξ1=0.05。隔震层参数为:橡胶垫水平刚度kb=3×103kN/m，阻尼比ξb=0.20;普通Maxwell 型阻尼器刚度k0=1.5×103kN/m，松弛时间λ=1/μp=0.1 s。采用平稳白噪声作随机地震激励，取其功率谱系数S0=0.013 87 m2/s3，分别计算设置与未设置Maxwell 耗能阻尼器，隔震结构上部各层相对于隔震层的位移、速度响应方差以及阻尼器响应方差，计算结果见表1。

从表1 可以看出:设置Maxwell 耗能阻尼器隔震结构顶层和隔震层的位移、速度响应方差比无阻尼器隔震结构顶层和隔震层的位移、速度响应方差分别降低了51.1%、38.1%和53.02%、39.57%，说明设置Maxwell 耗能阻尼器混合被动控制隔震结构的减震效果更好，并能有效减小隔震结构主体侧移。另外，算例还求得Maxwell 耗能阻尼器响应方差精确解为423.9 kN2。

表1 计算结果Tab.1 The calculation results

5 结 语

本文对设置Maxwell 耗能阻尼器隔震结构平稳响应分析进行了系统研究。针对多层结构，利用柔度法建立结构运动方程，然后将上部结构相对位移向量按第一振型展开，通过扩阶［12-15］将结构运动方程转化为一阶状态运动方程组。最终，基于复模态方法对该状态方程进行精确解耦，严谨地获得了单层Maxwell 粘弹阻尼隔震结构上部各层相对于隔震层以及隔震层相对于地面的位移、速度响应，并获得了粘弹性阻尼器阻尼力设计值(这一点常被工程技术人员所忽视)，进而为粘弹阻尼隔震结构的抗震设计、阻尼器耗能减震优化设计提供了较好的补充和参考。

［1］ 薛茹，杨秋枝.基底隔震技术的研究与进展［J］.焦作大学学报，2002，16(1):57-58.

［2］ 潘东辉，于国有，张德强.隔震高层结构的悬臂梁模型的地震反应研究［J］.工程力学，2012，29(5):115-211.

［3］ BUCKLE I G，MAYER R L.Seismic isolation:history，application，and performance-a world view［J］.Earthquake Spectra，1990，6(2):161-201.

［4］ 胡智渊.粘弹性阻尼器隔震结构的振动控制研究［J］.华东交通大学学报，2008，25(3):32-35.

［5］ 骆年红，杨庆丽，周强.位移相关摩擦阻尼基础隔震结构地震分析［J］.西安建筑科技大学学报:自然科学版，2012，44(6):773-778.

［6］ 吴晶波，韩江水，余文渊.设置磁流变阻尼器的智能基础隔震建筑的半主动控制分析［J］.四川建筑科学研究，2013，39(4):231-234.

［7］ 韦捷亮，庄鹏，王孟鸿，等.超弹性形状记忆合金棒的力学性能试验［J］.建筑技术开发，2014，41(5):33-38.

［8］ ZAMBRANO A，INAUDI A，et al.Modal coupling and accuracy of modal strain energy method［J］.Journal of Engineering Mechanics，1996，122(7):603-612.

［9］ 陈欧阳.非对称非经典结构实空间解耦和地震作用取值方法及其在多高层隔震结构中应用［D］.广西大学土木建筑工程学院，2013.

［10］李创第，黄天立，李暾，等.带TMD 结构随机地震响应分析的复模态法［J］.振动与冲击，2003，22(1):36-39.

［11］李创第，陈欧阳，葛新广，等.多层隔震结构近似实空间解耦及地震作用取值［J］.广西大学学报:自然科学版，2013，38(4):785-794.

［12］黄东梅，李创第，朱乐东.基础隔震结构基于设计反应谱的地震作用取值［J］.西安建筑科技大学学报:自然科学版，2007，39(4):504-511.

［13］肖烨，范亚坤，易萍华.基于模态扩阶法的结构损伤识别方法应用研究［J］.建筑科学，2011，27(7):62-64.

［14］瞿祖清，常文君.非线性特征问题计算的扩阶法［J］.力学与实践，1997，19(6):26-27.

［15］刘福顺，郭鹏，王超，等.一种模态振型的直接扩阶方法［J］.工程力学，2012，29(8):28-32.