一种模糊函数时频差联合估计快速算法

王志平，闫 涛

（中国电子科技集团公司第五十四研究所，河北石家庄050081）

一种模糊函数时频差联合估计快速算法

王志平，闫 涛

（中国电子科技集团公司第五十四研究所，河北石家庄050081）

直接相关时延估计方法仅适用于接收站和辐射源都相对静止的情况，若接收信号存在多普勒频差则会严重影响时差（TDOA）估计精度，为解决相关时延估计方法的局限性，采用基于模糊函数的时频差联合估计方法，并针对模糊函数计算量巨大的问题，提出一种变时频分辨率峰值搜索方法。利用GPU并行计算架构实现来实现算法，以提高算法效率，加快算法收敛速度。仿真试验结果表明了算法的有效性。

时差估计；模糊函数；运动平台；多普勒频差

0 引言

无源定位的基本技术主要有时差（TDOA）定位技术、测角（AOA）交叉定位技术和多普勒频差（FDOA）定位技术等［1，2］。多站TDOA定位技术由于可以获得较高的定位精度，同时对接收系统的要求较低，易于组网，能适用于宽带低谱密度信号等优点，被广泛应用［3，4］。

互相关法是最经典的时延估计方法［5，6］，它通过信号的自相关函数滞后的峰值估计信号之间延迟的时间差。这种方法简单易懂，容易实现，但不足之处是对非平稳信号、可变时延和多普勒频差信号的估计误差大，为解决直接相关时延估计方法的局限性，提出一种基于模糊函数的时频差联合估计方法，以消除多普勒频差对时差估计的影响，同时估计出的频差值还可用于频差（FDOA）定位［7，8］，以进一步提高无源定位精度。互模糊函数可以看成是时间和频率两维相关函数，计算量较大，限制了其应用范围。

1 基于模糊函数的时频差联合估计

1.1 多普勒频差对时差估计的影响

辐射源与接收站之间存在相对运动，相应的信号接收数学模型可近似表示为：

式中，fd表示信号间的频率差，D表示信号时延，n1（t）、n2（t）表示噪声。

估计施瓦茨不等式，信号x1（t）与x2（t）的互相关函数可表示为：令θ＝2πfdT，则：

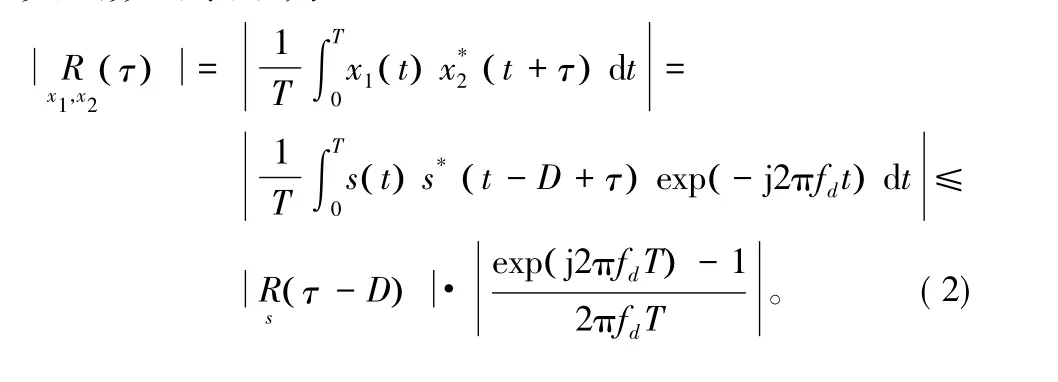
1.2 模糊函数时频差估计

模糊函数［9，10］是时延和多普勒频移联合估计问题的主要处理工具之一，其基本方法是将一路信号进行频移后，再用之与另一路信号进行相关运算。

信号x1（t）与x2（t）的二阶互模糊函数为x1（t）频移之后与x2（t）的相关输出，如式（4）所示：

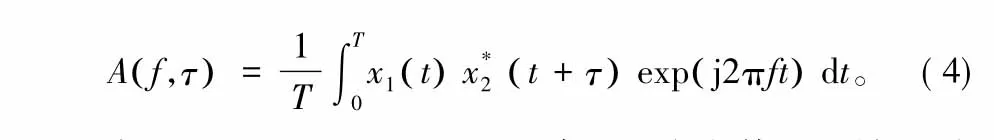
如果s（t）、n1（t）、n2（t）都是零均值的，并且在经历了任意的时延τ和频移f之后，仍然能够保持相互独立，则当T趋于无穷大时，

其中，

上式即为源信号s（t）的二阶自模糊函数，根据三角不等式以及施瓦兹不等式，可得：

也就是说：

因此，时延D和多普勒频移fd的估计可以由函数Ax1，x2（f，τ）最大值所对应的变量f和τ给出，即：

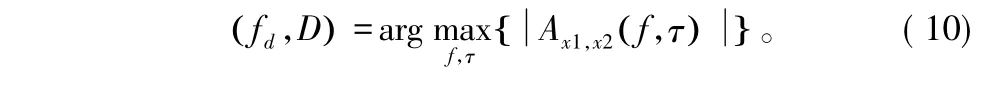
2 变时频分辨率模糊函数峰值搜索

2.1 模糊函数时频差精度及计算效率分析

在实际应用中，可按式（11）实现离散时间采样信号模糊函数计算：

（11）

由上式可以看出，当数据长度一定时，单次计算量不变，算法运算时间与计算次数成正比，设时差搜索宽度T、频差搜索宽度F，时差搜索分辨率Δt，频差搜索分辨率Δf，单次计算时间m，则算法计算时间：

增大时差频差搜索步进可以减小计算次数，但会严重影响时频差估计精度，模糊函数时频差估计精度如式（13）和式（14）所示，其中b为信号带宽，bn为信道带宽（噪声带宽），t为信号持续时间，tn为等效相关累积时间，SNR为测量模块有效输入信噪比。

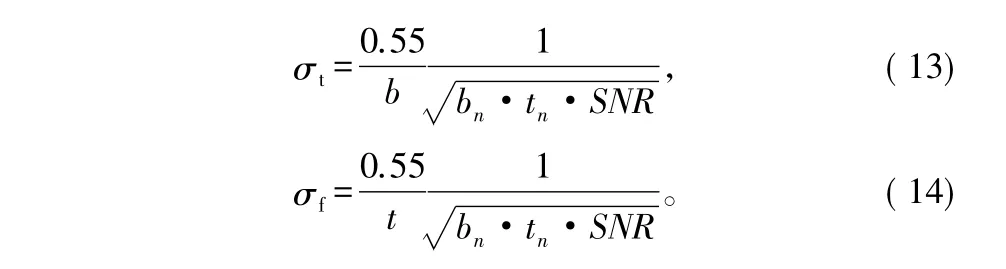
由式（13）和式（14）可知，信号持续时间t越长，带宽b越宽，时频差估计精度就越高，但同时时频差联合搜索所需的时频差分辨率也就越高，一般情况下模糊函数搜索所需的时差搜索步进应小于1/b，频差搜索步进应小于1/t，否则可能会漏掉相关峰值。

2.2 变时频分辨率峰值搜索方法

根据最优化理论，提出一种可变时频分辨率峰值搜索方法，首先采用大的步进进行搜索，后面的每次搜索都在上次搜索的峰值附近更小的搜索范围内，逐步减小搜索步进，提高时频差分辨率进行搜索，以期望得到最优结果。如图1所示，假设区域中心为理论最优值，图中每个点代表一次计算，同时在算法实现时，采用了基于GPU并行并行计算架构，大大减小了搜索时间。算法处理流程如下所示：

①根据接收站位置、目标活动范围和目标最大速度等先验信息确定初始时差频差搜索范围［t0t1］和［f0f1］；

②对数据进行滤波抽取和时间截短处理，只取数据的部分有效带宽和持续时间进行模糊函数相关峰值粗搜索，减小信号带宽和时间后可以采用较大的时差和频差搜索步进，有效减小计算次数，并降低单次计算所需的时间；

③设时差搜索峰值位置为T peak，搜索步进T step，频差搜索峰值为F peak和F step，在［T peak－T step T peak＋T step］和［F peak－F step F peak＋F step］的时频差搜索范围内，对全部带宽和持续时间的完整数据，以更小的时频差搜索步进（时频差搜索步进首次应初始化为1/2t和1/2b），重新计算模糊函数，搜索相关峰值；

④判断时频差搜索步进是否小于时频差估计指标要求，若不小于，则将搜索步进减小一半，重复步骤③，若小于指标要求，则输出当前峰值对应的时频差结果。

图1 变时频分辨率峰值搜索与经典方法比较示意图

3 仿真结果及分析

3.1 仿真结果

仿真条件设置：接收站坐标（－25，0）和（25，0）km，沿x轴方向匀速直线运动，速度都为100 m/s，辐射源坐标（0，50）km，速度为0；

①窄带FM信号，带宽50 kHz，信号长度100ms，结果如图2所示，可以看出模糊函数时差估计结果明显优于相关法；

②宽带BPSK信号，带宽5 MHz，信号长度7μs，结果如图3所示；

③BPSK信号，带宽1 MHz，信号长度1 s，采样率2 MHz，信噪比10 dB，理论时差1μs，理论频差－5 Hz，时差搜索范围－50～50μs，频差搜索范围－50～50 Hz，时差搜索精度0.05μs，频差搜索精度0.1 Hz，结果如表1所示。

图2 窄带FM信号试验仿真结果

图3 宽带BPSK信号试验仿真结果

表1 本文方法与常规方法性能比较

3.2 结果分析

由结果可以看出，对于累积时间较短的信号，直接相关和模糊函数时差估计结果几乎没有差别；而对于长累积时间的情况，经模糊函数校正频差后的时差估计结果精度要明显优于直接相关的时差估计结果，与理论分析一致，同时本文方法大大减少了搜索时间。

4 结束语

研究了多普勒频差对时差估计的影响，对基于模糊函数的时差估计方法进行分析和推导，并提出一种可变时频分辨率峰值搜索方法，以减小计算量，提高算法效率。仿真结果说明本文方法能够有效消除多普勒频差对时差估计影响，减少模糊函数峰值搜索时间，验证了上述分析的正确性。

［1］胡来招.无源定位［M］.北京：国防工业出版社，2005.

［2］Ho K C，Chan Y T.Geolocation of a Known Altitude Object from TDOA and FDOA Measurements［J］.IEEE Transactions on Aerospace and Electronic Systems，1997，33（3）：770－783.

［3］Ho K C，Chan Y T.Solution and Performance Analysis of Geolocation by TDOA［J］.IEEE Transaction Aerospace and Electronic Systems，1993，29（4）：1311－1322.

［4］王成，李少洪，王鑫全，等.测时差被动定位算法的研究［J］.系统工程与电子技术，2011，23（11）：9－12.

［5］Chen C K，Garder W A.Signal Selective Time－difference of Arrival Estimation for Passivelocation ofMan－made Signal Sources in Highly Corruptive Environment，Part 1：Theory and Method［J］.IEEE Trans.On Signal Processing，1992，40（5）：1185－1197.

［6］Chen C K，Garder W A.Signal Selective Time－difference of Arrival Estimation for Passivelocation ofMan－made Signal Sources in Highly Corruptive Environment，Part2：Algorithms and Performance［J］.IEEE Trans.On Signal Processing，1992，40（5）：1168－1184.

［7］徐海源，吕守业，韩涛.三星多普勒频差无源定位方法及定位精度分析［J］.宇航学报，2010，31（7）：1832：1837.

［8］卢鑫，朱伟强，郑同良.多普勒频差无源定位方法研究［J］.航天电子对抗，2008，24（3）：40：43.

［9］朱伟强，黄培康，张朝.利用互模糊函数联合估计的双星高精度定位技术［J］.系统工程与电子技术，2006，28（9）：1294－1298.

［10］孙正波，叶尚福.利用互模糊函数实现卫星干扰源定位［J］.电波科学学报，2004，19（5）：525－529.

Fast Time Delay Estimation Algorithm Using Ambiguity Function

WANG Zhi－ping，YAN Tao
（The 54th Research Institute of CETC，Shijiazhuang Hebei050081，China）

The time delay（TDOA）estimation algorithm by correlation match can be applied only to stationary scenario，while the existence of Doppler can seriously deteriorate the accuracy of TDOA.To address this issue，a TDOA estimation algorithm by using ambiguity function is proposed，and a peak searchingmethod of time－frequencymulti－resolution is provided.A GPU parallel calculation architecture is applied to the implementation of the algorithm to improve the efficiency.The simulation result demonstrates the effectiveness of the algorithm.

TDOA estimation；ambiguity function；moving platform；Doppler shift

TN971

A

1003－3114（2015）04－52－4

10.3969/j.issn.1003－3114.2015.04.13

王志平，闫 涛.一种模糊函数时频差联合估计快速算法［J］.无线电通信技术，2015，41（4）：52－55.

2015－03－30

王志平（1983—），男，工程师，主要研究方向：无源定位、通信信号处理。闫涛（1985—），男，工程师，主要研究方向：无源定位、通信信号处理。