孤子内波模拟及其声场影响研究

邵云生

（海军驻上海地区航天系统军事代表室，上海，214061）

孤子内波模拟及其声场影响研究

邵云生

（海军驻上海地区航天系统军事代表室，上海，214061）

相对理想的孤子内波模型和局部性特征的实测数据，使得孤子内波影响声传播的研究相对滞后。通过美国麻省理工学院开发的MΙTgcm海洋模式，结合物理海洋和海洋声学领域的相关理论，对孤子内波进行了模拟和分析，并基于此进行了内波对声场的影响研究。相比传统方法，该方法能够得到更为合理和全面的孤子内波数据，为声场方面研究奠定基础。

孤子内波；MΙTgcm；声场起伏

1 引言

由于特殊的地理和水文环境，南海是世界上内波最丰富的区域之一。内波可产生洋面的汇聚和分散，因此可通过合成孔径雷达（SAR）观测到[1]。孤子内波是以波包形式存在的，每一波包内都由多个波形组成，振幅逐渐减小，随后是一个很长的尾迹。由于海水内部的小密度差异，孤子内波会导致大振幅波动，产生水平和垂直方向的强剪切，在南海，内波振幅可达百米[2]。海水稳定分层和扰动源是孤子内波产生的两个基本条件。台湾和菲律宾之间的吕宋海峡是连接南中国海和太平洋最重要的通道，复杂的海底山结构和剧烈的潮流，是南海北部孤子内波生成的扰动源。研究表明，吕宋海峡的特殊海底地形对内波的产生起着重要的作用，两座海底山之间的距离及它们的高度都是内波产生的重要因素[3]。丰富的海洋内波在吕宋海峡西侧生成后向西传播，直至较浅的大陆架区域[3,4]。孤子内波有着各种积极和消极的影响，对其的研究和预报一直是物理海洋领域的重要课题[5-8]。

孤子内波可以导致温跃层剧烈起伏，引起声速剧烈变化，从而对海洋声场造成重要影响。在海洋声学领域，很多孤子内波影响声场的研究工作[7,9-15]已开展。其中，选择合适内波模型非常重要。目前，通常使用统计模型和KdV模型描述内波，但是统计模型多适合于线性内波，KdV模型用于描述弱非线性孤子内波，而南海北部孤子内波具有强非线性特征，需要更合适的内波模型描述。MΙTgcm海洋模式基于Navier-Stockes型方程，通过流速、温度、盐度等变量进行建模，可以进行非静力模拟，能够保持强非线性特征，特别适合孤子内波模拟。因此，根据吕宋海峡地形及潮流条件，通过MΙTgcm建模仿真，能够得到声场研究所需的孤子内波背景数据。

文献[16]中，给出了应用MΙTgcm海洋模式研究孤子内波声学效应的新方法，进行了孤子内波存在下的声传播损失分析。本文在此基础之上，通过施加合理的初始和驱动条件，利用MΙTgcm海洋模式得到了更为符合实际的孤子内波模型数据，并基于此从多角度研究了孤子内波在浅海对宽带声场的影响，总结了影响规律。

2 MITgcm海洋模式与孤子内波模拟

MΙTgcm模式是由麻省理工学院开发的大气-海洋通用环流模式，全称为MΙT General Circulation Model，可以模拟各种尺度海洋运动。孤子内波作为一种中小尺度运动，垂直方向运动剧烈，需要进行非静力假设，MΙTgcm能满足这一条件，适合用来研究孤子内波。模式基于以下控制方程：

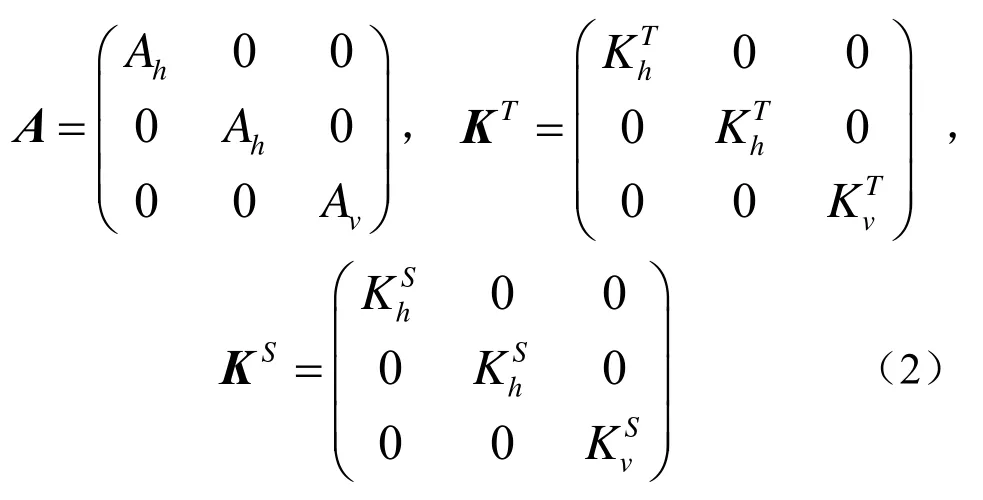
为粘性和温盐的扩散系数矩阵，下标h和v分别表示水平和垂直方向，为垂直方向单位矢量。方程组（1）中6个方程有7个未知量，联合状态方程构成封闭方程组。

由于南海北部孤子内波传播方向大体是由东向西，并且海底地形有一定二维特征，为减少计算量考虑，可以在二维区域内对孤子内波进行模拟。整个计算区域有四个边界：东边界、西边界、海面和海底。海面采用最简单的刚盖近似；东边界为驱动边界，施加潮流条件；西边界根据模拟的具体情况进行相应处理。为避免边界造成虚假的反射波，在东西两个开边界处增加一个海绵吸收层。海底采用slip条件，由于南海北部孤子内波的南北长度超过200 km，中心在21°N左右，由此选取吕宋海峡在20.5°N～21°N地形数据的纬向平均作为二维模拟中的海底地形，除了吕宋海峡外都设为3 700 m的平海底，如图1所示，吕宋海峡处采用近似海底，整个海底采用slip条件。

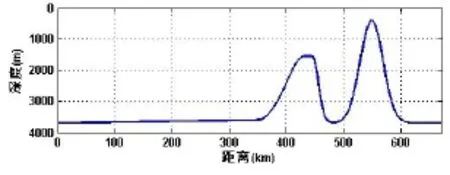
图1 孤子内波模拟中海底地形

为使整个计算区域内水量守恒，东西开边界施加相同的边界条件，潮流驱动条件使用根据TPXO 7.2数据的调和分析预测值，为包含M2、S2、N2、K2、K1、O1、P1共8个主要分潮的混合潮。图2给出2001年5月份的潮流预测曲线图，蓝线表示潮流的东西向分量，红线表示南北向分量，其中（a）只包含4个半日潮部分；（b）中只包含4个全日潮部分；（c）包含所有8个分潮的混合潮。预测曲线有明显的半月周期变化，分别有2次高潮和2次低潮。根据图中数据，混合潮东西和南北分量的最大值比值为6.58，说明东西方向潮流分量在混合潮中绝对占优。

初始条件包括温度、盐度和水平方向海流的初始值，盐度初始值设为定值34.5‰。温度、海流初始值根据SODA数据得到。模拟中采用笛卡尔坐标网格，包括水平网格和垂直网格。水平网格东西长度为300 m，共2 240个网格；南北长度2 000 m，共1个网格；垂直方向共有3 700 m，前2 000 m网格长度为10 m，后面1 000 m网格长度20 m，其余网格长度40 m。模式中取。根据CFL原则，取时间步长为4 s。

图2 预测性模拟中使用的潮流驱动条件

图3 5月3～12日实测与预测性模拟温度对比图

图3中（a）为2001年亚洲海国际实验（ASΙAEX 2001）期间于（117o16.975’ E，21o36.871’ E）处的温度实测值，（b）为相近位置处模拟得到的温度值，模拟结果在内潮周期和孤子内波生成时间上与实测值对应较好。随着边界潮流强度的变化，生成的孤子内波幅度会有相应变化，说明太平洋的潮流条件对孤子内波的重要作用。由于只是二维模拟，并且没有考虑南中国海大陆坡、太平洋黑潮入侵、台风等因素影响，模拟结果存在可允许范围内误差。

进行模拟和实测结果的相关性分析。截取第4～5日两天的模拟结果作为小潮期样本，截取第9～10日两天的模拟结果作为大潮期样本，分别用这两个样本与实测值进行滑动相关分析。在相关性分析过程中减掉了平均温度，以消除了背景平均温度对相关系数的影响。如图4（a），蓝线为小潮期样本与实测值得相关系数，红线为大潮期样本与实测值的相关系数。由于减掉了平均温度，相关系数减小了，并可能出现负数。温度场的潮汐周期性使我们得到的相关系数也体现出一定潮汐周期。小潮期相关系数在4日01时26分达到最大值0.52，大潮期相关系数在8日22时16分达到最大值0.51，与期望的相关系数达最大值的时刻差别不大，说明了模拟结果的合理性。图5（b）是根据相关性分析所得结果微调后，模拟与实测结果的18℃等温线对比图，模拟与实测在孤子内波周期和幅度上符合较好。其它等温线比较，有类似结论。

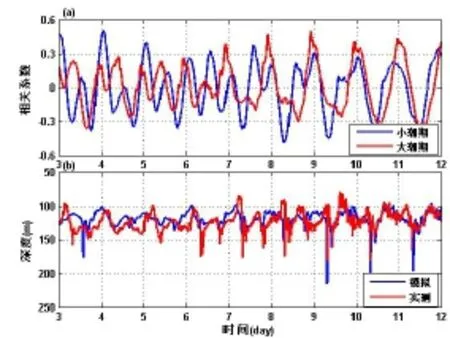
图4 (a)大小潮时模拟结果与实测相关系数(上图) (b)模拟结果与实测18℃等温线比较(下图)

3 孤子内波声场影响研究

为了说明孤子内波对声场的影响规律，利用MΙTgcm海洋模式对单个孤子内波进行模拟，截取50 km区域2个小时的运行结果作为背景场，截取区域为300 m水平海底，图5为所截取的0 min和120 min时的温度场分布图。在0 min孤子内波大约处于26 km处，120 min后，孤子内波运行至约4 km处。为方便计算，定义有无孤子内波影响时的声传播损失之差为传播损失差。

图5 0 min和120 min时的温度分布图

假设声源处于0 km深30 m处，考察中心频率为400 Hz、带宽为100 Hz信号的声场分布。假设海底声速1 600 m/s，海底密度1 700 kg/m3，海底衰减0.2 dB/λ。利用RAM-PE计算得到传播损失分布，如图7所示，其中（a）为无孤子内波时的传播损失。由于海深只有300 m，声波将频繁接触海底，大约每5 km就有一个由海底反射而形成的高声强区。（b）、（c）、（d）分别为0 min、60 min和120 min时传播损失差的情况，从中可以看出，孤子内波对其后区域的声场会产生较大影响，最大起伏处大于10 dB，传播损失差有比较规律的波形，孤子内波改变了声线的传播路径，影响了声场的干涉结构。由于孤子内波的波长大约有10 km，远大于两个干涉增强区之间的距离，说明孤子内波会一致地影响大部分声线。当孤子内波通过接收点时会对传播损失产生较大影响，而一旦越过接收点，影响就会大大降低。

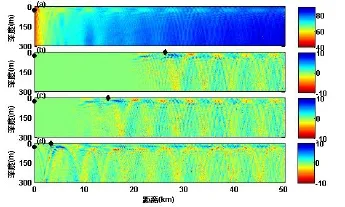
图6 （a）无孤子内波时的传播损失,（b）、（c）、（d）分别为0 min、60 min和120 min时的传播损失差,图中圆点为声源位置、菱形处为孤子内波中心的位置

进一步地，考察12 km、40.5 km和43.5 km三个位置处的传播损失差随时间的变化，如图7（a）、（b）和（c）。整个120 min内，孤子内波将越过处于12 km的高声强区，因此（a）体现了孤子内波从无到有的影响过程，在孤子内波经过时，传播损失标准差形成的条纹明显有一个下沉的趋势，在上方形成一个传播损失增大的区域，而后的影响比较稳定。大体上（b）、（c）两个位置一个是无孤子内波影响时的高声强区，另一个为无孤子内波时的低声强区，这两个位置的声场在这120 min内一直受孤子内波影响。

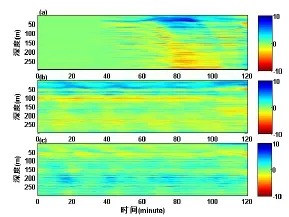
图7 12 km、40.5 km和43.5 km处传播损失标准差随时间变化图

图8为30 m深度的传播损失差随时间的变化，图中黑线为孤子内波中心的移动轨迹。可以看到，在孤子内波本地的传播损失差相比其它位置要大的多。并且，传播损失差较大的区域基本能连成一条线，与孤子内波的运行轨迹完全符合。传播损失差在孤子内波之后的区域呈现条纹形状，且具有一定周期性。

图8 30 m深传播损失差随时间变化图，黑线表示孤子内波中心的运动轨迹

4 结论

海洋声学研究中考虑的海洋运动数据通常来源于两种情况：一是理想模型，比如孤子内波的KdV模型，能够满足基本的研究，但对于更为精细的分析研究，很多时候不能满足；二是实测数据，实测数据有两方面局限性，首先，实测数据一般比较昂贵，另外实测数据有空间和时间的局限性，不能得到所关心的任意时间和地点的数据。而本文方法能很好地克服上面两种数据来源的局限性。只要对研究内容进行充分的理论论证，就能得到比较符合实际、时空上比较全面的模型数据。

MΙTgcm结合RAM声场计算模型，对浅海孤子内波声场影响进行了研究。通过计算结果对比得出：孤子内波对其后区域声场产生重大影响，起伏幅度大于10 dB，由于声线基本都要碰触海底，在孤子内波的传播过程中，对所有声线产生一致影响，使得声场出现比较有规律性的变化。MΙTgcm模拟产生孤子内波传播过程中全方位数据，由此可以计算得到任何时刻声场结果，为孤子内波声场影响规律研究提供极大方便，具有重要的研究意义。基于本方法，可以进一步开展孤子内波声场影响的三维效应研究。

数值模拟海洋环境研究声传播规律有很多方便，也有其自身缺点，要努力提高海洋模拟的准确度。本文方法还有很多需要改进的地方，比如三维模拟、更加符合实际的运行条件（初值、边界、海底）以及增加数据同化机制等。

[1]Global Ocean Associates.An atlas of oceanic internal solitary waves:south china sea[R].Prepared for Office of Naval Research,2004.

[2]Katsnelson B G,Petnikov V,Lynch J.Fundamentals of shallow water acoustics[M].Springer,2012

[3]Li Q.Numerical assessment of factors affecting nonlinear internal waves in the south china sea[J].Progress in Oceanography,2014,121(2):24-43.

[4]Liao G H,Yuan Y C,Arata K,et al.Analysis of internal tidal characteristics in the layer above 450m from acoustic doppler current profiler observations in the luzon strait[J].Science China:Earth Sciences,2011,54(7):1078-1094.

[5]Ezer T,Heyman W D,Houser C,et al.Modeling and observations of high-frequency flow variability and internal waves at a Caribbean reef spawning aggregation site[J].Ocean Dynamics,2011,61:581-598.

[6]Helfrich K R,Melville W K.Long nonlinear internal waves[J].Annu.Rev.Fluid Mech.,2006,38:395-425.

[7]Kumar P V H,Rao A R,Anilkumar K,et al.Low-frequency internal waves and their influence on transmission loss variability[J].Nat Hazards,2011,57:643-656.

[8]Simmons H,Chang M H,Chang Y T,et al.Modeling and prediction of internal waves in the South China Sea[J].Oceanography,2011,24(4):88-99.

[9]Badiey M,Katsnelson B G,Lin Y-T,et al.Acoustic multipath arrivals in the horizontal plane due to approaching nonlinear internal waves[J].JASA,2011,129(4):el141-el147.

[10]Duda T F,Lin Y-T,Reeder D B.Observationally constrained modeling of sound in curved ocean internal waves:Examination of deep ducting and surface ducting at short range[J].JASA,2011,130 (3):1173-1187.

[11]Farmer D M,Alford M H,Lien R C,et al.From luzon strait to dongsha plateau:stages in the life of an internal wave[J].Oceanography,2011,24(4):64-77.

[12]Katsnelson B G,Yu A.Malykhin,et al.Rearrangement of the horizontal space-time structure of the sound field in shallow water in the presence of moving internal waves[J].Ocean Acoustics,2011,57(3):368-374.

[13]Sridevi B,Murty T V R,Sadhuram Y,et al.Ιmpact of internal waves on the acoustic field at a coastal station off paradeep[J].East Coast of Ιndia.Nat.Hazards,2011,57(3):563-576.

[14]任云.存在内波条件下南海声场时间相关特性研究[D].中国科学院声学研究所,2010.

[15]王少强.海洋孤子内波及其引起的声场起伏规律-理论模型与数值模拟研究[D].中国科学院声学研究所,2006.

[16]高善国,李风华.南中国海北部非线性内波及声场研究[C].中国科学院声学研究所第四届青年学术会议,2012.