薄壁箱梁非线性温度空间效应分析

柳磊，欧旗祥

（1.山东省交通规划设计院，山东 济南250031；2.上海慧加软件有限公司，上海200433）

0 引言

近年来，我国已建桥梁上的病害时有发生，在众多病害中最为常见的是梁体裂缝。根据裂缝产生的位置不同，可将其分为腹板裂缝、顶板裂缝和底板裂缝等。顶板裂缝主要是由箱梁的畸变变形和横向弯曲引起［1］。在活载作用下若顶板横向弯矩过大，并且没有布置横向预应力钢束，很容易引起顶板的纵向裂缝。此外，我国旧版的桥梁规范对温差应力估计不足，使桥梁设计偏于不安全［2～3］。国外规范的温度梯度模式比我国规范的内容更详细，且温度荷载值也更大［4，11－12］，这也是经常发生顶板纵向裂缝的原因之一。JTG D62—2004《公路钢筋混凝土及预应力混凝土桥涵设计规范》［10］中对活载作用下的桥面板计算有明确的规定，但对梯度温度作用下的桥面板计算没有说明，在桥面板配筋设计中也往往忽视了梯度温度效应。

目前，对箱梁梯度温度的研究普遍采用二维有限元法［5－6］，仅对截面的纵向整体效应分析；也有部分学者采用 Ansys有限元软件进行研究［2－7］，但研究重点主要放在了应力的分布和局部的受力上，对桥面板配筋设计提供的帮助有限。

文章采用的空间网格模型以六自由度梁单元为基础，不仅能够对箱梁空间效应进行准确分析，而且得到的内力和应力与桥梁规范紧密结合，可直接用于桥面板配筋设计［1］。相比于 Midas、Ansys等大型有限元软件，空间网格模型的优势体现在：（1）分析结果是设计人员常用的内力数值，无需二次应力积分得到内力，可直接用于结构配筋设计；（2）结构模型的单元数量少，占用计算机资源小，计算运行时间短。

1 非线性温度曲线

桥梁结构中的梯度温度是由日照温差引起，且受辐射强度、桥梁方位、日照时间、地理位置等因素影响，在桥梁结构上形成三维的温度场 T（x，y，z，t）。但在梯度温度分析时，通常认为温度沿桥梁纵向分布一致，可将三维温度场简化为二维温度场，即沿着截面横向和竖向两个方向的温度。此外，公路桥梁一般都设悬臂板，腹板因悬臂的遮荫终日不受日照，横桥向的温差变化也不大，因此对桥梁温度的分析重点放在了竖向温度场上［8］。

JTG D60—2004《公路桥涵设计通用规范》（简称《桥涵通规》）中的梯度温度如图1所示。对于混凝土结构，当梁高H＜400 mm时，A＝H－100 mm；当H≥400 mm时，A＝300 mm，图中t为混凝土桥面板的厚度［9］。《桥涵通规》仅对桥梁顶板的温度模式进行了规定，并没有对底板的温度模式提出要求，而英国BS5400对底板的温度荷载也有详细规定，有关底板是否考虑梯度温度及如何考虑都需要深入的研究［14－15］。

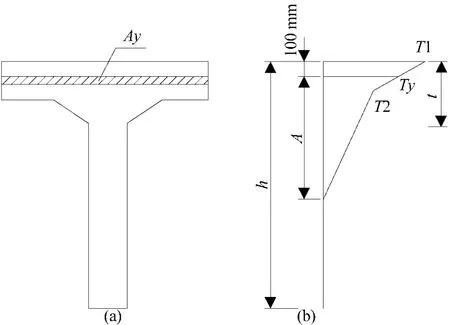
图1 《桥涵通规》中的梯度温度图

从图1可见，《桥涵通规》中的梯度温度属于非线性温度，对静定结构而言，该温度荷载仅产生温度自应力，对超静定结构还将产生温度次应力。

采用二维有限元法对梯度温度进行计算是比较常用的做法，采用该方法能够得到纵向温度应力沿截面高度的分布情况，但无法得到箱梁截面的横向框架效应，而空间网格法能弥补这一不足。

2 工程实例分析

选取某座三跨预应力混凝土连续梁桥进行非线性温度的纵横向效应分析，该桥的桥面铺装为9 cm厚沥青混凝土，桥梁的梯度升温线形如图2所示。

桥梁跨径布置为37＋60＋37（m），箱梁顶板宽为 12.75 m，底板宽为7.0 m，跨中梁高为 1.8 m，中支点梁高为3.6 m，梁高按照二次抛物线变化，箱梁的横截面尺寸如图3所示。

文章采用慧加（WisePlus）商业软件进行有限元分析，并可提供完全的空间分析。结构模型共有2180个节点和4323个单元，结构模型如图4所示，对模型中的纵梁单元和桥面横向单元施加图2所示的温度荷载。

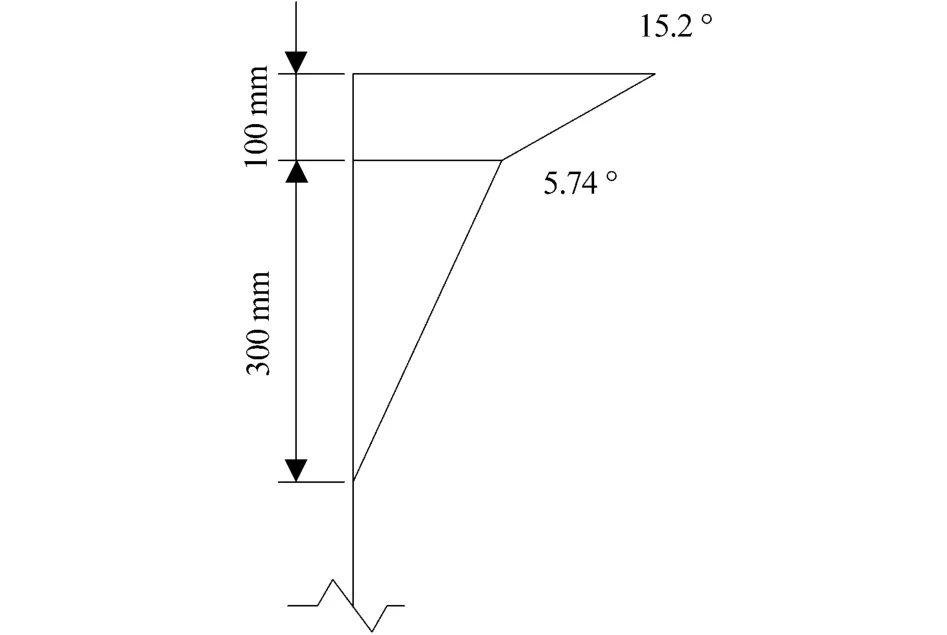
图2 计算实例的梯度温度曲线图

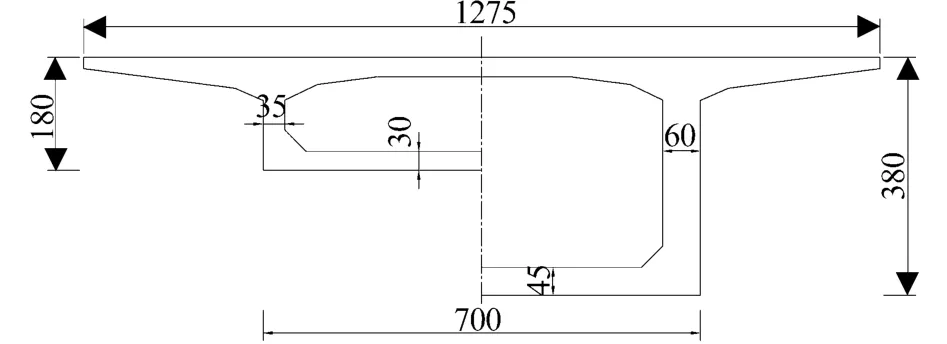
图3 箱梁横截面图／cm

图4 空间网格模型（左半跨）图

由于箱梁结构具有对称性，因此仅选取箱梁截面上具有代表性的位置进行分析，箱梁截面上的选取位置如图5所示。

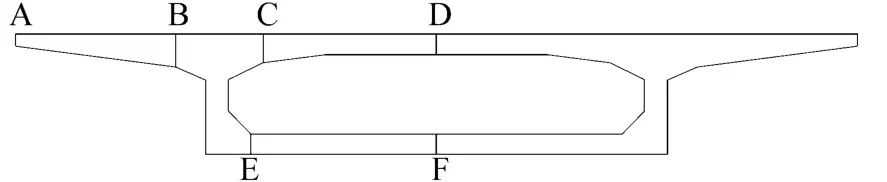
图5 温度应力计算点图

3 非线性温度的纵向效应

3.1 箱梁顶板A～D点的应力结果

在梯度升温荷载作用下，箱梁顶板A～D点的上下缘温度应力如图6所示，图中正值表示拉应力，负值表示压应力。

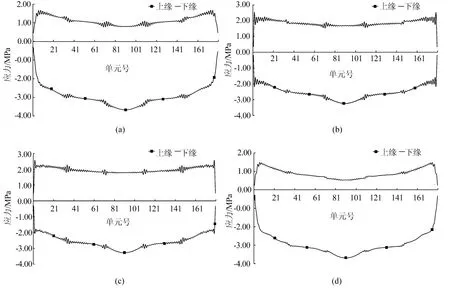
图6 梯度升温下箱梁顶板A-D点纵向应力图

从箱梁顶板A～D点的应力图形看，梯度升温时顶板上缘受压，截面横向不同位置的压应力基本相同，数值在3～4 MPa范围内。顶板下缘受拉，拉应力约为1 MPa，边支座附近拉应力约为2 MPa。顶板上下缘的应力差别主要是由温度自应力公式中的第三项tyαcEc引起，顶板上下缘对应的温度值ty不同，得到的温度自应力也不相同。

通过计算，汽车荷载作用下的截面顶板上缘的最大拉应力为2.39 MPa，与实例工程的温度拉应力相当；而汽车荷载的最大压应力为2.51 MPa，小于实例工程的温度压应力。

3.2 箱梁底板E、F点的温应力结果

在梯度升温荷载作用下，箱梁底板E、F点的上下缘温度应力如图7所示，图中正值表示拉应力，负值表示压应力。

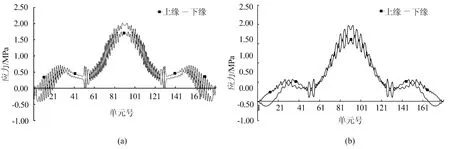
图7 梯度升温下箱梁底板E-F位置纵向应力图

从箱梁底板E、F点的应力图形看，梯度升温时底板的上下缘均受拉，中跨跨中的拉应力最大，应力数值在2 MPa左右。

通过计算可知，汽车荷载作用下的截面底板下缘的最大拉应力为4.36 MPa，大于实例工程的温度拉应力。

3.3 桥梁整体竖向变形

在梯度升温作用下，桥梁的竖向变形曲线如图8所示。在梯度升温作用下，两边跨的变形趋势为上翘，中跨的变形趋势为下挠。边跨的最大上翘数值为2.45 mm，中跨的最大下挠数值为5.87 mm。中跨最大变形数值与跨径比为 5.87／60000＝1／10221，可见由温度荷载引起的结构变形较小。

4 非线性温度的横向框架效应

4.1 横向框架的应力计算结果

空间网格模型能够反映温度荷载的横向框架效应，分别选取边支座、中墩和中跨跨中三个位置进行分析，计算结果分别如图9、10和11所示，图中正值表示拉应力，负值表示压应力。

通过三个位置的温度应力图形可以得出：

（1）箱室内的顶板横向下缘拉应力较大，在边支座和中跨跨中位置达到3 MPa，且均位于闭合箱室的中间位置。这是由于除温度自应力外，横向框架的约束作用还引起了温度次应力，且温度次应力数值较大，二者叠加后使得顶板横向下缘的拉应力数值较大。顶板横向的上缘均受压，压应力在4 MPa左右。

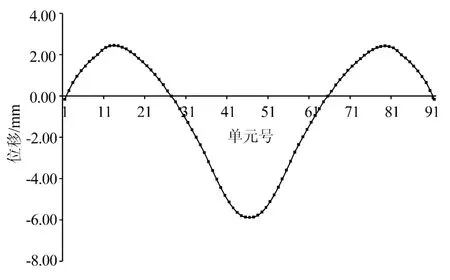
图8 梯度升温作用下桥梁的竖向位移图

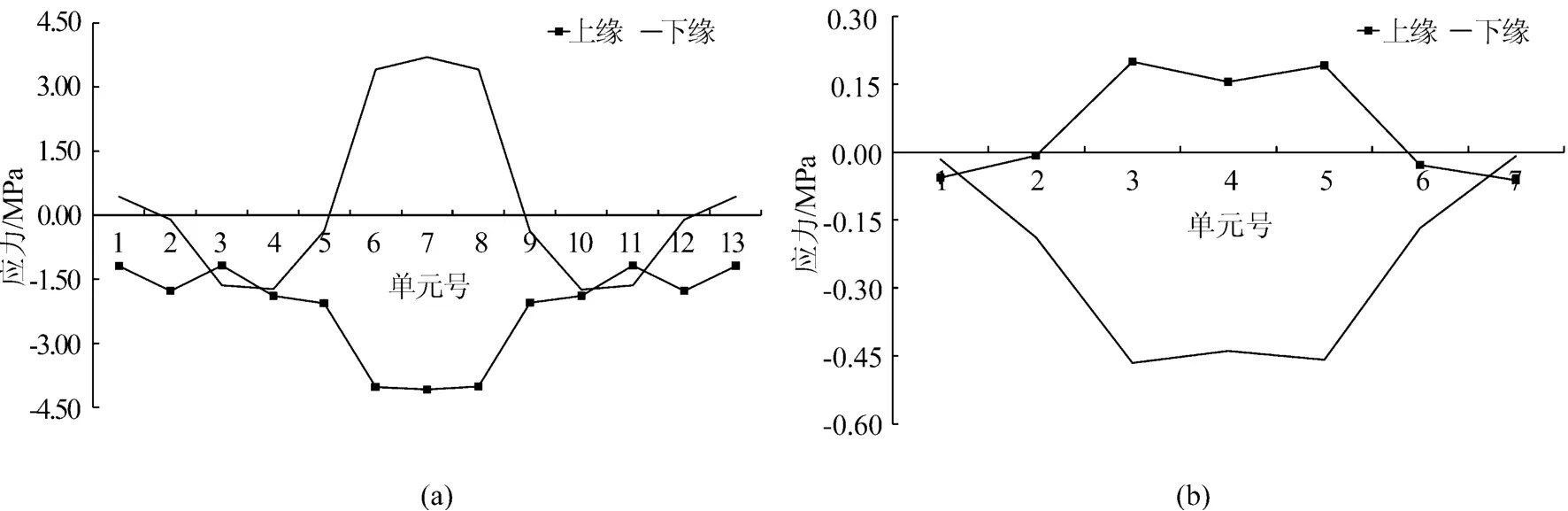
图9 边支座处的顶底板横向应力图

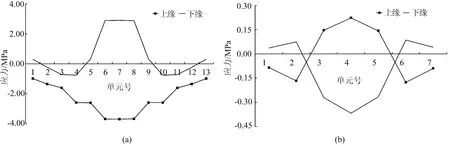
图10 中墩处的顶底板横向应力图

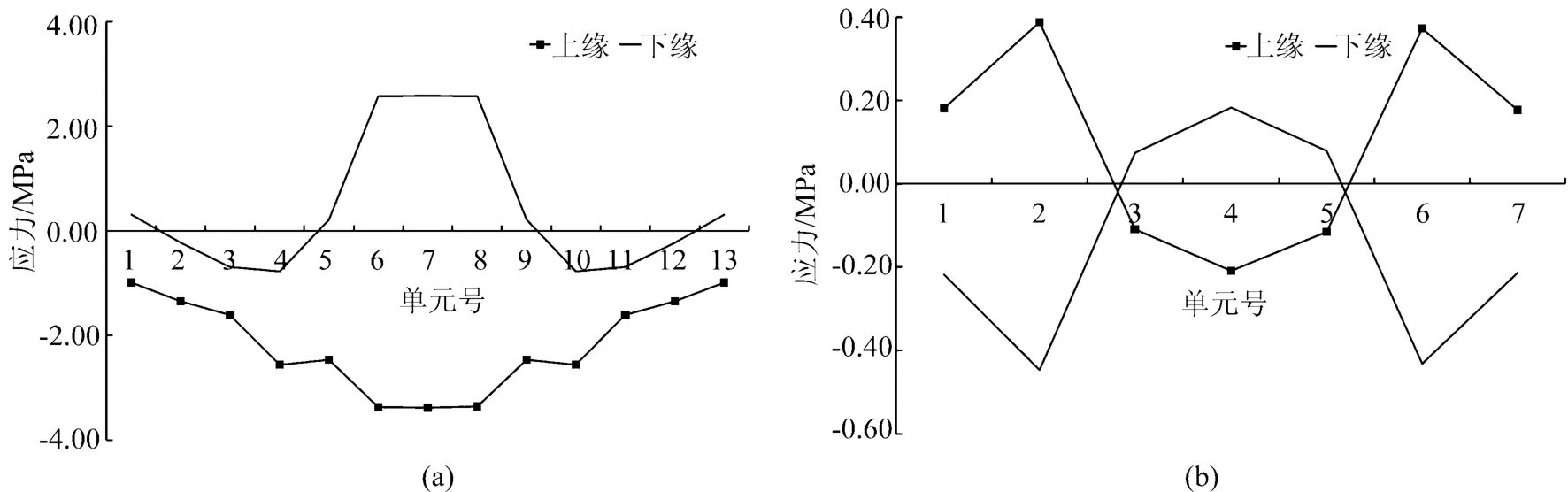
图11 中跨跨中处的顶底板横向应力

（2）箱梁悬臂板的横向温度应力较小，相比箱室内的温度应力有明显的下降，这是由于悬臂部分为静定构件，其温度应力仅由温度自应力产生。

（3）箱室内的底板上下缘的温度应力相对较小，最大不超过0.4 MPa。从图2的温度曲线来看，梯度温度的作用范围达不到箱梁的底板，也就没有温度自应力的产生，仅有框架约束作用引起的温度次应力。

通过计算，汽车荷载作用下横向框架的应力数值为：悬臂根部上缘最大拉应力为2.7 MPa，顶板下缘最大拉应力为4.7 MPa，底板下缘最大拉应力为0.87 MPa，可见梯度温度应力与汽车活载应力相当。

4.2 横向框架竖向变形

在梯度升温作用下，选取中跨跨中来列出横向框架的竖向位移结果，如图12所示。

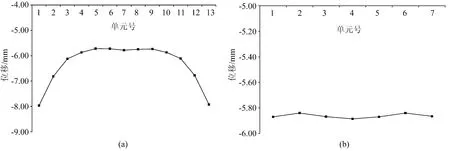
图12 中跨跨中处横向框架的竖向位移图

从横向框架的竖向位移图看：

（1）顶板悬臂端部的竖向位移为－8.0 mm，除悬臂外其余各点的竖向位移在－5.87 mm左右，悬臂部分相比箱式部分的竖向位移更大，超出比例为（8－5.87）／5.87＝36.3%。这是因为悬臂部分为静定构件，在梯度升温作用下悬臂的上层纤维膨胀变长，下层纤维膨胀变形相对较小，导致悬臂形成向外的弯曲角度，表现为悬臂端部的竖向位移最大。

（2）底板各点的竖向位移均在－5.87 mm左右，各点的竖向位移相差不大。

（3）顶底板和腹板构成的横向框架（不含悬臂）各点的竖向位移很接近，均在－5.87 mm左右，而悬臂部分的变形相对较大，说明横向框架的整体性好于悬臂部分。

5 结论

文章采用空间网格法对实例工程的非线性温度荷载进行计算，通过分析后可得到以下结论：

（1）纵向温度应力顶板的上缘受压，下缘受拉；底板的上、下缘均受拉，拉应力最大值位于中跨跨中。

（2）横向温度应力顶板的横向上缘受压，下缘受拉；悬臂板和底板的横向应力均较小。

（3）梯度温度应力值与活载应力值相当，应对其足够重视。

（4）梯度升温作用会引起边跨上翘和中跨下挠，变形量总体较小；在升温作用下横向框架的整体性好于悬臂部分。

（5）对于一些重要桥梁，建议结合气候条件对温度模式进行适当的修正，使结构分析更加贴近桥梁的实际受力。

［1］徐栋.混凝土桥梁结构实用精细化分析与配筋设计［M］.北京：人民交通出版社，2013.

［2］邓成刚，高波，戴捷.混凝土箱梁空间受力梯度温度影响分析［J］.现代交通技术，2014，11（1）：22－25.

［3］魏霞，郭峰祥，徐向锋.新旧规范梯度温度荷载对箱梁结构受力的影响［J］.桥梁建设，2010（2）：55－57.

［4］卢傲，张春华.中欧规范梯度温度对混凝土桥面板影响对比分析［J］.中外公路，2013，33（3）：122－126.

［5］黄建强.公路混凝土桥梁常见病害与成因分析及处治方法［J］.公路交通科技 －应用技术版，2014（1）：46－49.

［6］罗阳青，杜召华，蒋鑫.连续箱梁顶板裂缝成因分析研究［J］.湖南交通科技，2012，38（1）：63－66.

［7］邓成刚，高波，戴捷.混凝土箱梁空间受力梯度温度影响分析［J］.现代交通技术，2014，11（1）：22－25.

［8］项贻强，龚世康.考虑竖向和横向温度梯度的桥梁温度应力分析［J］.中国市政工程，2008，1（131）：29－31.

［9］刑中凯，谢高潮.混凝土箱形截面梁桥温度梯度分析［J］.中国西部科技，2008，7（28）：42－43.

［10］郭敬姐，舒国明.PC箱梁温度效应研究及ANSYS仿真模拟［J］.公路交通科技，2006（6）：73－76.

［11］叶见曙，贾琳，钱培舒.混凝土箱梁温度分布观测与研究［J］.东南大学学报，2002（6）：788－793.

［12］JTG D60—2004，公路桥涵设计通用规范［S］.北京：人民交通出版社，2004.

［13］JTG D62—2004，公路钢筋混凝土及预应力混凝土桥涵设计规范［S］.北京：人民交通出版社，2004.

［14］BS 5400 Steel，Concrete and Composite Bridges.Part2：Specification for Loads［S］.London：British Standards Institution，1990.

［15］BS 5400 Steel，Concrete and Composite Bridges.Part4：Code of Practice for Design of Concrete Bridges［S］.London：British Standards Institution，1990.