Full Spark框架扰动的定理
王亚飞,杨守志
(汕头大学数学系,广东汕头515063)
Full Spark框架扰动的定理
王亚飞,杨守志
(汕头大学数学系,广东汕头515063)
框架扰动理论是框架研究中的一个活跃分支,本文针对Full Spark框架的扰动问题,首先研究了框架的扰动性质,并说明框架与Full Spark框架区别.然后讨论Full Spark框架扰动问题,给出了Full Spark框架扰动的定理.最后,进一步研究了在算子意义下Full Spark框架的一些等价性质.
框架;Full Spark框架;扰动;算子;等价
0 引言
框架的概念在1952年就已经由Duffin和Schaeffer[1]在研究调和Fourier级数时引入.在这种定义下,框架具有与基相似的性质,即利用框架可以表示空间中的任意元.然而不同的是框架的表示方法不唯一.在以后的半个世纪里,框架理论未引起重视. 1986年,三位小波方向的先驱Daubechies,Grossman和Meyer[2]发现可以利用框架将函数展开成类似标准正交基展开的级数的形式.自此,框架才受到越来越多的关注.这种关注主要集中于两个大方向:一种是作为泛函分析的一个分支;一种是研究具体特殊形式的框架,如L2(R)上的小波框架.
在实际应用中,主要是对有限维框架进行研究,并影响着许多领域,如信号重构、编码理论、稀疏信号处理等.在这些应用中,有一些需要构造一类特殊性质的框架,如在M维框架元素中要求每M个子元素是线性无关的.具有这类性质的框架成为Full Spark框架.Spark的概念是Donoho和Elad在文献[3]中首次提出的.但是Spark的概念在其它一些文献也有类似的表述,如Gorodnitsky和Tao[4]、Tang和Nehorai[5].后来在文献[6-8]中,对Full Spark框架的构造、分类等方面进行了研究,但是关于Full Spark框架特有的性质还没进行讨论.
框架扰动理论是框架研究中的一个重要的方向.扰动是指对已知的框架做一个微小的摄动,其仍是一个框架.Casazza和Christensen在框架扰动性上做过许多重要性的工作[9-11].根据已有的框架扰动的知识,在有限维空间中框架、Riesz基和Riesz框架存在一个扰动结果,见性质1,但是这个性质对于特殊的Full Spark框架并不成立.对于此,本文给出了Full Spark框架下的一个扰动结果;最后在算子意义下讨论了Full Spark框架一些等价性质.
1 相关基础知识
本节给出一些基本概念.N表示自然数集,即N={1,2,…};R表示实数集;C表示复数集;H,HM分别表示Hilbert空间、M维Hilbert空间;〈·,·〉表示H的上的内积;l2(N)表示所有满足

的序列c={cj}j∈N组成的空间.
定义1:设{fk}k∈N为可分的Hilbert空间H的点列.如果存在常数A,B>0,使得

则称{fk}k∈N为H的一个框架,其中常数A,B为框架{fk}k∈N的框架上、下界.
定义2:设{fk}k∈N为可分的Hilbert空间H的点列,若,如果存在常数A,B>0,使得对任何{ck}k∈N∈l2成立

则称{fk}k∈N为H的Riesz基,其中常数A,B为Riesz基{fk}k∈N的Riesz上、下界.
在框架中,如果(1)式中A=B,则称框架{fk}k∈N为紧框架;如果A=B=1,则称框架{fk}k∈N为Parseval紧框架;如果对于所有的k,l∈N,||fk||=||fl||,则称框架{fk}k∈N为等范框架;如果对于所有的k∈N,||fk||=1,则称框架{fk}k∈N为单位范框架.如果(1)式仅右不等式成立,则序列{fk}k∈N称为Bessel点列.如果框架{fk}k∈N去掉任何一个元素后不再是框架,则称该框架{fk}k∈N为恰当框架.
对于M维Hilbert空间,(1)式中的框架上界B是平凡存在的,也就是说,在这种有限维集合中,框架的概念仅要求框架下界A是大于0的.
定义3:假设为空间HM上的框架,称算子S=TT*:HM→HM为框架的框架算子,定义如下:

定义4:在矩阵F中,称它的最小线性相关子集的列的个数为该矩阵的Spark[3],即

根据线性代数的知识,如果一个M×N矩阵是Full Spark,则它的每个M×M子矩阵都是非奇异的,也就是说它是满秩的.因此,该矩阵就可以看作是一个框架.
对于HM上的框架,称该框架为Full Spark框架,即是说框架矩阵F是Full Spark的.
在文献[12]中,有限维空间中框架、Riesz基和Riesz框架上存在如下一个扰动结果,
性质1:设为界为A,B的框架(Riesz基或Riesz框架),如果存在常数λ1,λ2,μ≥0满足,且对任意有限数列c1,c2,…,cn,n∈N,n≤N有


注:有限维框架一定是Riesz框架,故性质1可以只考虑有限维框架与Riesz基.但性质1对于Full Spark框架并不成立,反例如例1.
例1:在R2中,设,容易证明都是R2上的框架,而且是Full Spark框架.通过计算可以求得框架的下界为19,又容易验证对任意实数列c1,c2,…,c4有

显然在λ1=1/2,λ2=0,μ=1意义下,上式满足性质1的扰动条件(对于n<4的情况类似),但是又很容易发现框架不是Full Spark框架.
例1对于性质1表明Full Spark框架失效,则说明在扰动意义下,框架与Full Spark框架是有区别的.要想考虑在Full Spark框架下的扰动性,就需要把性质1中的条件中再加强约束.
2 Full Spark框架的扰动结果
作为本文的重点部分,本节给出了Full Spark框架扰动的结果.
定理1:设为HM上界为A,B的Full Spark框架,如果存在常数λ1,λ2≥0满足max{λ1,λ2}<1,且对任意有限数列c1,c2,…,cn,n∈N,n≤N,有

证明:Full Spark框架是一类特殊的框架,故按照上述性质中的方式扰动后得到的仍是一个框架,取性质1的特殊情况,即μ=0时,则扰动后的框架界为A(1-λ1)2/(1+ λ2)2,A(1+λ1)2/(1-λ2)2.因此,本定理,只需证明扰动后的仍为Full Spark即可,也就是说要证明中任意M列都是线性无关的.
注:如果性质1中考虑的,即含有无限个元素的框架,那么仍按照性质1的扰动条件,结论一样成立,即性质1中Full Spark框架的元素个数可以是无限多的.
3 算子意义下Full Spark框架的扰动
定理2:设为HM上的Full Spark框架,L为有界线性可逆算子,那么设是HM上的Full Spark框架.
推论1:设为HM上的Full Spark框架,A为N×N的非奇异矩阵,那么是HM上的Full Spark框架.
推论2:设为HM上的Full Spark框架,那么形成的矩阵经过行的初等变换后仍是HM上的Full Spark框架.
注:矩阵作行(列)初等变换,实际上是在该矩阵左(右)乘以一个初等矩阵.初等矩阵又是非奇异的,根据推论1显然可得到推论2.
推论3:设F=[AM×MBM×N-M]为CM上的Full Spark框架,那么AM×M-1F=[IMAM×M-1BM×N-M]仍为CM上的Full Spark框架,而且还是一个最优稀疏的Full Spark框架.
证明:根据定理2,显然AM×M-1F仍是一个Full Spark框架,且与原框架在表示CM上是等价的.下面只要说明这个框架是在所有M×N类型的Full Spark框架下是最优稀疏的即可.
根据文献[6]所述,所有M×N类型的Full Spark框架中存在最优稀疏Full Spark框架,该框架中总共有M(M-1)个零元素.而推论3中矩阵AM×M-1F的零元素个数为M(M-1)个,而且不可能有多余这个数的零元素存在,即块矩阵AM×M-1BM×N-M中不可能存在零元素.为了说明这个结论,只需用反证法证明.
假设AM×M-1BM×N-M中存在一个零元素,位置在矩阵AM×M-1BM×N-M的(i,j)处,那么它处框架矩阵AM×M-1F的第M+j列,表示该列向量(第j列)的形式为

其中,*表示非零常数.如果用上述列向量替换矩阵AM×M-1F=[IMAM×M-1BM×N-M]中的块IM第i列向量,得到
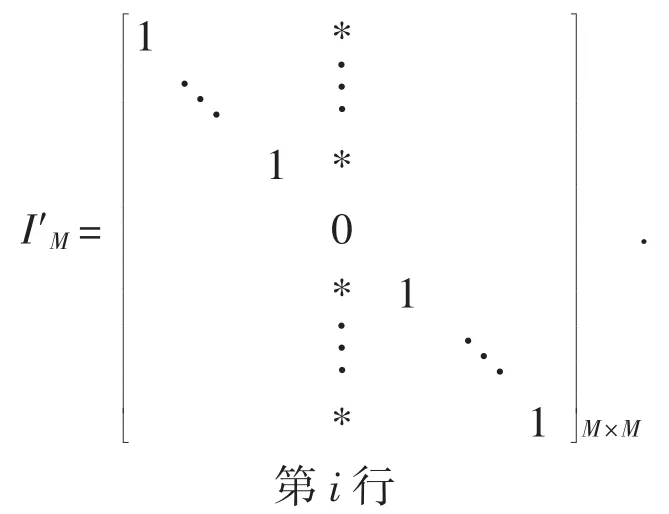
其中省略部分全是0元素.不难发现此矩阵的行列式为0,这与AM×M-1F是Full Spark框架矛盾.故假设不成立,即块矩阵AM×M-1BM×N-M中不可能存在零元素.证毕.
注:推论3对于Full Spark框架的构造是有重要意义的.因为它的逆形式就是一般Full Spark框架的构造方法.
4 总结及展望
在向量空间中,框架与基有类似的性质,即可以将空间中的每一个元素表示成一组框架元素的线性组合,但各框架元素之间并不要求是线性独立的,也就是说可以将框架看成一组基加上一些元素构成的.因此,若一组框架元素确定,在已知的空间中的元素由框架的表示法不唯一.这在数字信号处理等实际应用中具有重要作用.Full Spark框架在实际运用中具有最大鲁棒性、能够检测信号零点等优势,应用前景广阔,研究价值较高.本文在扰动与等价方面研究了Full Spark框架的性质,在例证了原有的扰动定理在Full Spark框架后,提出了针对Full Spark框架的扰动定理,而后在算子意义下进一步研究了Full Spark框架的扰动性质.这些研究结果使得Full Spark框架的理论更加丰富,应用中对具体Full Spark框架的选择自由度更多.
在本文的研究结果的基础上,可以结合现有Full Spark框架的构造方法均是通过特殊矩阵这种情况,通过逆用推论3的过程,从理论深度上对Full Spark框架的构造作进一步构造研究.
[1]Duffin R J,Schaeffer A C.A class of nonharmonic fourier series[J].Trans Amer Math Soc,1952,72(2):341-366.
[2]Daubechies I,Grossmann A,Meyer Y.Painless nonorthogonal expansions[J].J Math Phys,1986,27(5):1271-1283.
[3]Donoho D L,Elad M.Optimally spares representation in general(nonorthogonal)dictionaries via minimization[J].Proc Natl Acad Sci,2003,100(5):2197-2202.
[4]Gorodnitsky I F,Rao B D.Sparse signal reconstruction from limited data using FOCUSS:a reweighted minimum norm algorithm[J].IEEE Trans Signal Process,1997,45(3):600-616.
[5]Tang G G.nehorai A.Performance analysis for sparse support recovery[J].IEEE Trans Inf Theory,2010,56(3):1383-1399.
[6]Alexeev B,Cahill J,Mixon D.Full spark frames[J].Journal of Fourier Analysis and Applications,2012,18(6):1167-1194.
[7]Candès E J,Romberg J,Tao T.Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information[J].IEEE Trans Inf Theory,2006,52(2):489-509.
[8]Fuchs J J.Sparsity and uniqueness for some specific under-determined linear systems[C]. Philadelphia:2005 IEEE International Conference on Acoustics,Speech,and Signal Processing,729-732.
[9]Casazza P G.The art of frame theory[J].Taiwanese J of Math,2000,4(2):129-201.
[10]Christensen O.A paley-wiener theorems for frames[J].Proc Amer Math Soc,1995,123(7):2199-2201.
[11]Casazza P G,Christensen O.Perturbation of operators and applications to frame theory[J].J Four Anal Appl,1997,3(5):543-557.
[12]李登峰,薛明志.Banach空间上的基和框架[M].北京:科学出版社,2007.
Theorem s on Perturbation of Full Spark Frames
WANG Yafei,YANG Shouzhi
(Department of Mathematics,Shantou University,Shantou 515063,Guangdong,China)
Perturbation theory of frames is an active branch of frames theory.In this paper,the perturbation of frames is studied,aiming at perturbation of full spark frames.The difference between frames and full spark frames is also illustrated.The perturbation of full spark frame is discussed and a perturbation theorem is given. Finally,the equivalences of full spark frames are further researched.
frames;full spark frames;perturbation;operator;equivalence
O 177.2
A
1001-4217(2015)01-0024-06
2014-10-19
王亚飞(1989-),男,河南沈丘人,在读硕士研究生.研究方向:小波分析与应用. E-mail:wyf0525@163.com

