微平面模型模拟ASR作用下混凝土力学行为

段 安，张大伟，ALNAGGAR Mohammed

（1.浙江大学建筑工程学院，浙江杭州310058；2.美国西北大学土木与环境工程学院，埃文斯顿60208）

微平面模型模拟ASR作用下混凝土力学行为

段 安1，张大伟1，ALNAGGAR Mohammed2

（1.浙江大学建筑工程学院，浙江杭州310058；2.美国西北大学土木与环境工程学院，埃文斯顿60208）

为了准确模拟发生碱-硅酸反应（ASR）的混凝土结构的复杂受力行为，在最新一代微平面理论的基础上，提出适于分析ASR作用下混凝土力学行为的微平面模型.修改了微平面应力边界和法向模量表达式，引入应力效应函数来模拟应力对ASR膨胀应变的影响.开发相应的动力显式算法，完成了该算法在有限元程序ABAQUS中的集成.对ASR作用下的混凝土试件力学性能和变形试验进行模拟可知，计算值与试验值吻合良好，验证了该模型的有效性.

微平面理论；碱-硅酸反应（ASR）；混凝土；ABAQUS

碱-硅酸反应（alkali-silica reaction，ASR）是混凝土结构劣化的主要原因之一[1].ASR是指水泥中的碱与骨料中的活性氧化硅成分反应，产生碱一硅酸盐凝胶.该凝胶具有强烈的吸水性，吸水后膨胀，从而引发混凝土开裂破坏.

现有对ASR作用下混凝土结构的力学分析大都基于张量形式的宏观本构模型[2-3].近年来提出的微平面理论[4-6]直接在微平面上建立矢量形式的应力-应变关系，概念清晰，能够描述混凝土的各种复杂受力行为，相对于传统宏观本构模型具有很大的优势[5-7].微平面理论最初由Zdeněk P.Bažant及其合作者于上世纪80年代提出[4]，经过30多年的研究，Bažant及其研究团队已逐步完善了这一理论，使之从最初仅适用于描述受拉开裂的第一代模型（M1），发展成为现在能够分析各种复杂受力行为的第七代微平面模型[5-6]——M7.目前，微平面模型因其独有的优越性和通用性，被广泛运用于混凝土结构的断裂、冲击、长期变形等各种复杂问题的数值分析当中[5-6].为了验证该微观本构模型是否适用于ASR作用下混凝土结构的受力分析，本文在微平面理论M7的基础上，引入ASR效应影响，提出适于分析ASR作用下混凝土力学行为的微平面模型.

1 第七代微平面理论计算流程与算法

混凝土作为一种非均匀的多相材料，骨料与水泥胶体之间的交界面是一个薄弱环节，在很大程度上直接影响混凝土的受力和变形性能.微平面理论基于混凝土的这种微观结构特性，把存在于骨料和水泥石之间的各个方向交界面定义为微平面（见图1（a）），并在各微平面上建立矢量形式的本构关系.微平面模型的计算流程（见图2）如下：取出材料的一个微元体，将其视为由一系列微平面按一定排布方式组成（见图1（b））.

1）根据动态约束，将宏观应变εij投影转换成各微平面应变分量（见图1（c））.设任意微平面的单位法向矢量为n，微平面内单位切向矢量为m和l，且满足正交关系：l=m×n，如图1（c）所示.微平面法向应变εN以及m 和l方向的切向应变εM、εL分别为

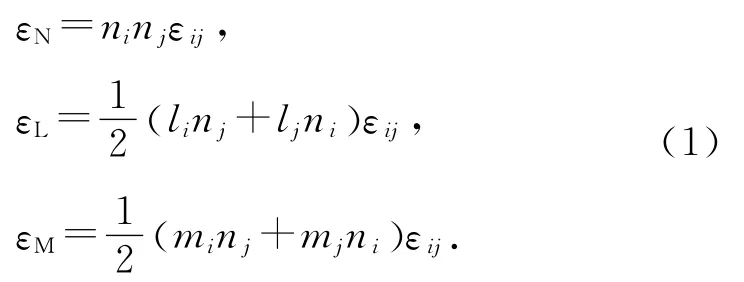
式中：ni、mi和li分别为n、m和l与整体坐标轴xi的夹角余弦.

2）由微平面上的应力-应变关系得到各微平面正应力σN及切应力分量σL、σM.M7引入4种应力边界来描述各微平面上的非线性应力-应变关系，包括正应力边界σbN、偏应力边界σbD、体积应力边界σbV和切应力边界σbT；若当前弹性计算的应力超过此时应变所对应的应力边界，则应力将垂直降至应力边界上，如图3所示.

3）基于虚功原理，将微平面应力转化为宏观应力σij：

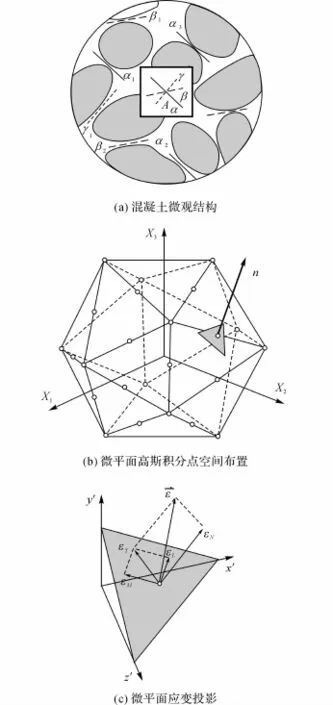
图1 微平面模型示意图Fig.1 Sketch of microplane model

式中：

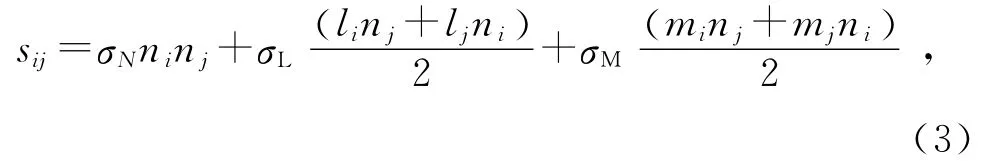
Ω为单位半球体表面，Nm为积分点数目，wμ为第μ个积分点的权重，本文取μ=37.

为了实现基于微平面理论的混凝土结构有限元分析，笔者编写了有限元软件ABAQUS的VUMAT子程序.该程序采用的显示算法如下.

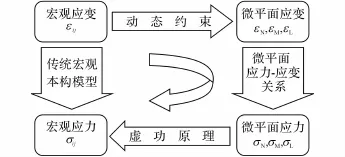
图2 微平面模型与传统宏观模型计算流程Fig.2 Flow of calculation between macro-and micro-levels

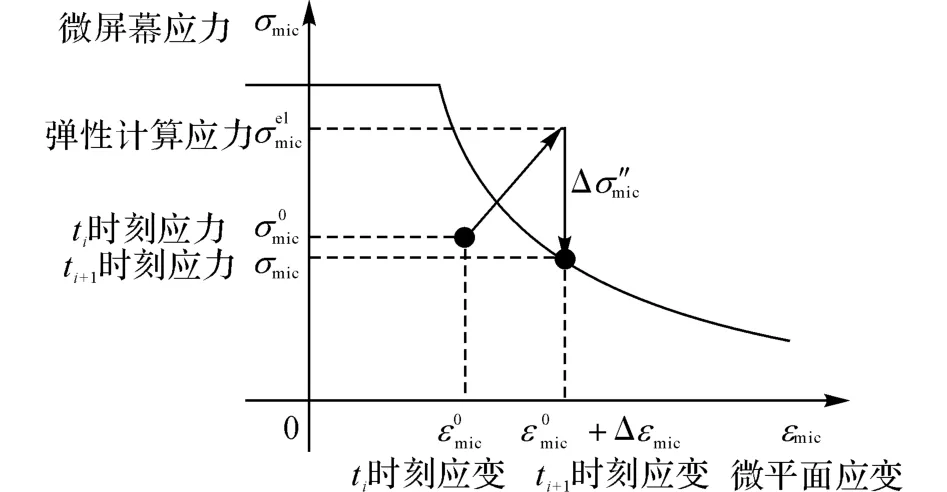
图3 微平面应力边界超越处理方式Fig.3 Vertical return to stress-strain boundary when boundary is exceeded

2）将法向应变分解为体积应变与偏应变，得到各微平面应变分量.

3）令εe=max（-0），计算体积应力边界，εe）.

5）计算法向弹性模量EN=fE），得到法向应力试算值

9）更新体积应力

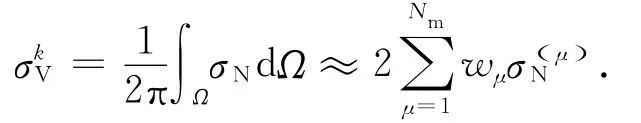
11）令

上述算法中，EN0=E/（1-2ν），ET=EN0（1-4ν）/（1+ν）（其中E为弹性模量，ν为泊松比）；fv、fD、fN、fT分别为体积应力边界、偏应力边界、法向应力边界和切应力边界函数，具体表达式见文献[5].

2 ASR作用下混凝土力学行为的微平面模拟分析

Alnaggar等[8]建立了ASR演化模型.该模型将ASR分为碱一硅酸盐凝胶的形成和凝胶吸水膨胀两个过程，推导出了凝胶吸水膨胀应变εGel的时变表达式，然后采用离散粒子格构模型（lattice discrete particle modeling，LDPM）[9-10]实现了ASR作用下的混凝土损伤模拟.由于LDPM所需的单元数量过大，对建模和计算效率不利.本文在原ASR演化模型的基础上，运用同属微观本构模型的微平面理论对ASR作用下的混凝土力学行为进行分析.

2.1 ASR损伤效应模拟

在微平面模型中引入ASR效应，微平面法向应变可以分解为

由于碱一硅酸盐凝胶吸水膨胀伴随着材料的破坏，本文通过削弱微平面应力边界和法向刚度来描述这一损伤行为.εTot可以分解为凝胶膨胀应变εGel和开裂应变εCr两部分[8]：

εCr是影响微平面应力边界和刚度受损的根源.受损的正应力边界可以表示为

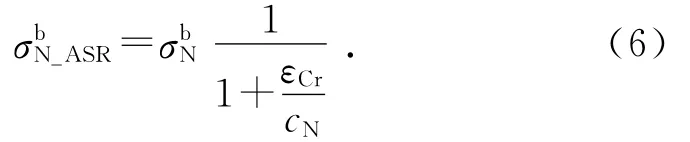
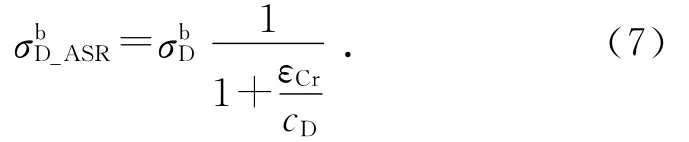
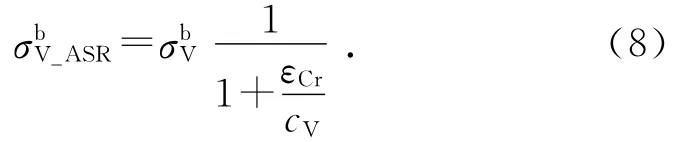
受损的法向弹性模量EN-ASR可以表示为

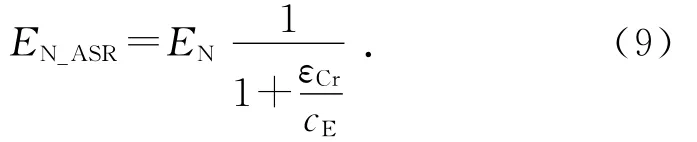
式中：cN、cD、cV和cE为微平面ASR损伤参数.

令

则开裂应变可以表示为

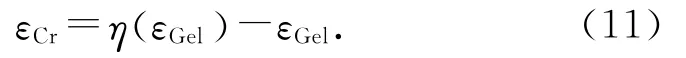
在本研究中，η（εGel）将通过LDPM计算获得.

2.2 应力效应的模拟

大量研究表明，压应力显著地抑制该方向上ASR所引起的混凝土变形[2，11]，大部分遭受ASR损害的结构（如大坝等）往往处于较高应力状态下.ASR效应模型有必要考虑应力状态的影响.令在第μ个微平面法向应力的作用下，该方向上的开裂应变εCr降低为H）·εCr，其中应力效应函数H采用以下形式：

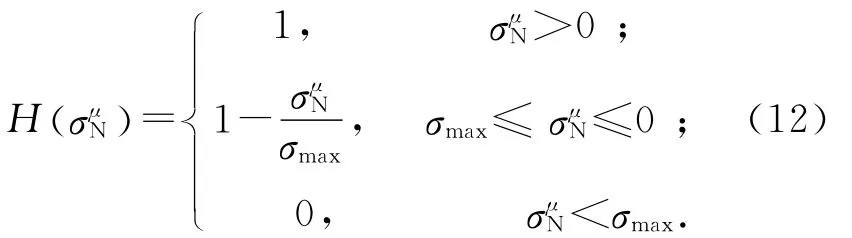
式中：σmax为应力影响阈值，当应力低于该值时，该方向ASR所引起的开裂应变将全部被抑制.

1）投影得到微平面应变及应变增量.

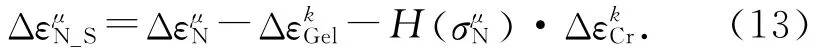
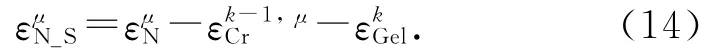
4）将第k-1时间步末第μ个微平面上的ASR引起的开裂应变代入式（6）～（9），计算受损的应力边界和法向模量.

5）更新并储存第μ个微平面上的ASR引起的开裂应变：

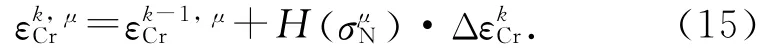
6）其余步骤与1章的算法一致.

2.3 模型参数标定

Multon等开展了系列试验来研究ASR引起的混凝土力学性能的衰变[12]和应力对ASR作用下混凝土试件变形的影响[2].本文首先利用其中的力学性能试验[12]对上述微平面ASR损伤参数进行标定，然后用文献[2]的试验数据对应力影响阈值σmax进行标定.

2.3.1 损伤参数的标定 Multon等[12]测量了ASR作用下混凝土试件在28、90、182、365 d时的弹性模量E、抗压强度fc和抗拉强度ft，监测了试件的应变随龄期T的变化历程.将该应变试验值εTot作为计算的输入，采用文献[8]的方法对试验所用的混凝土试件进行分析计算得到εGel，由式（5）可得开裂应变εcr，各应变如图4所示.

为了简单起见，在本研究中设cD=cV（因为这2个参数同时影响着抗压强度）.采用本文方法编写相应的VUMAT子程序，应用ABAQUS对该试验开展有限元模拟分析，然后进行参数标定，可得对于文献[12]中的混凝土，cN=0.4，cD=cV=0.009，cE=0.001 7.试验与模拟结果的对比如图5所示.图中，下标0表示28 d的测量值.

2.3.2 σmax的标定 Multon等[2]开展了如下试验：在28 d养护后，对圆柱体混凝土试件（高240 mm，直径为130 mm）施加了9种应力状态（持时450 d）：3组径向约束（无约束，3 mm厚钢环约束及5 mm厚钢环约束）.在每种约束下，施加了3种轴向荷载（0、10、20 MPa）.

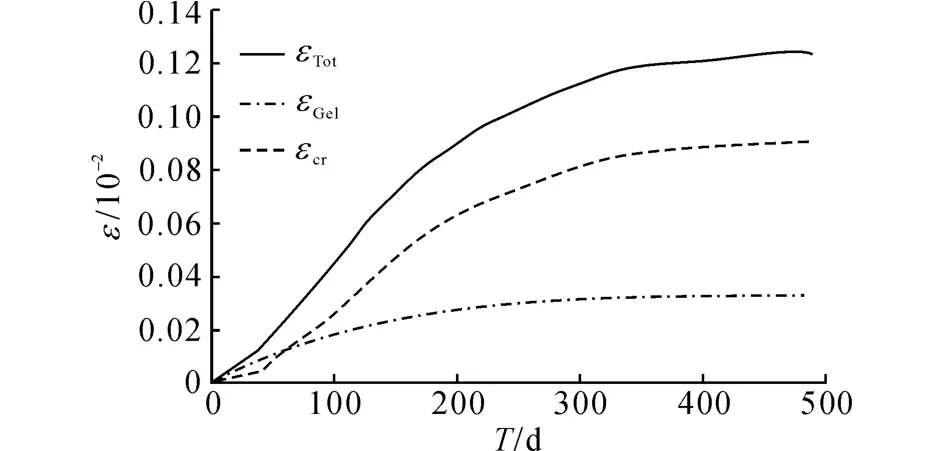
图4 各应变随龄期的变化历程Fig.4 Components of ASR expansion with time

为了模拟实际试验情况，须考虑收缩和徐变的影响.由于试件在整个试验用防水表层密封，可以认为只发生了自生收缩.在该研究中，采用CEB建议模型计算自生收缩，徐变采用的是B3模型[13]（具体计算过程见文献[8]）.为了明确收缩和徐变效应对试件变形的影响，本文模拟了2种情境：1）未考虑收缩和徐变；2）考虑了自生收缩和徐变效应.

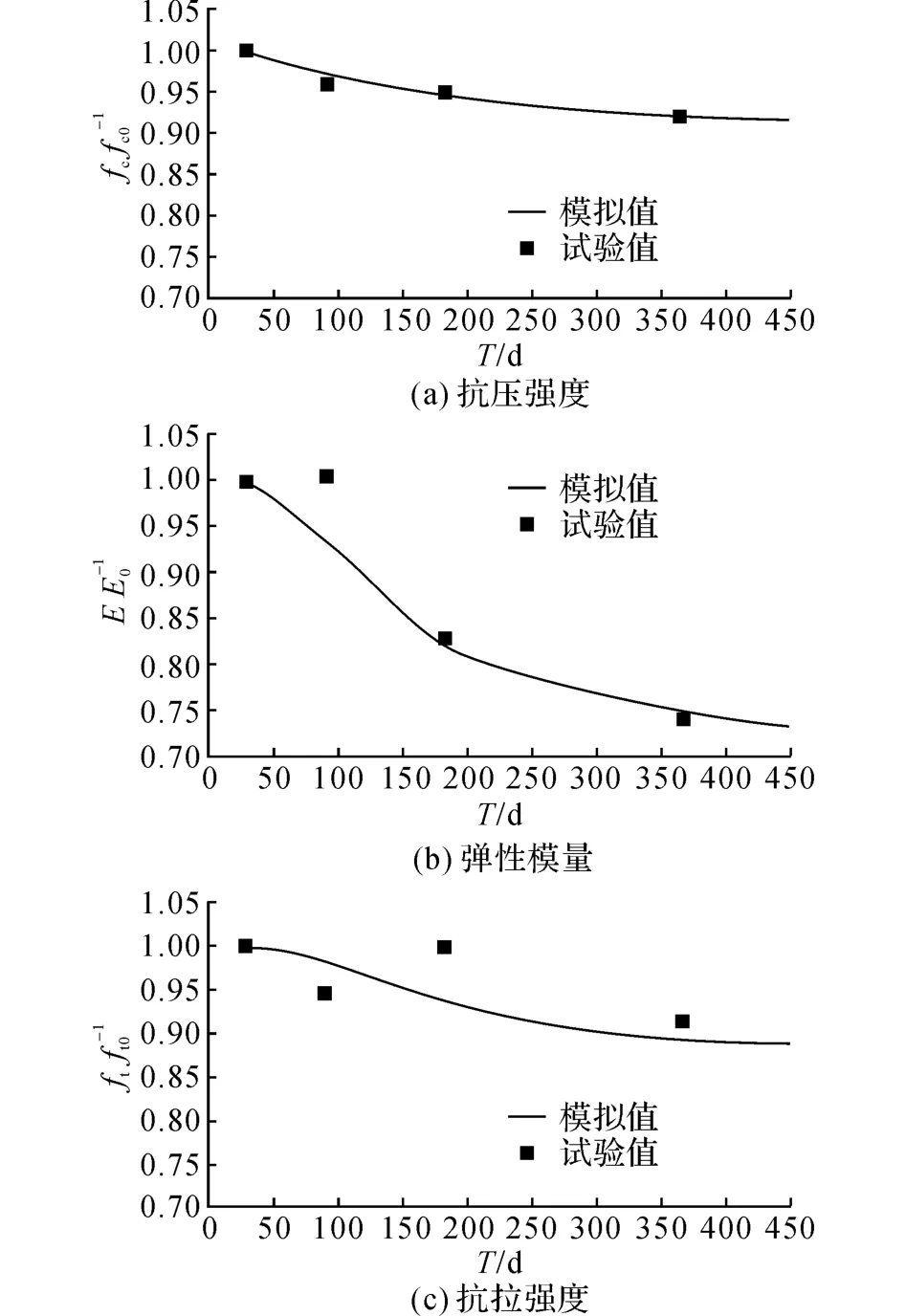
图5 力学性能衰变Fig.5 Simulated and measured mechanical properties evolution

文献[2]采用与文献[12]相同的ASR活性混凝土，因此2.3.1节中已标定的损伤参数将在本节及模型验证时保持不变.根据文献[8]的方法计算出凝胶膨胀应变和开裂应变，作为输入.根据文献[8]中推导凝胶膨胀应变的时变表达式来计算εGel；依据LDPM的计算结果（见图6），可将η（εGel）由下式回归：

由式（11）计算开裂应变及其增量，作为模型输入.首先计算无约束无轴向应力试件（此时无需考虑应力效应），由图7（a）可以看出，轴向应变εz的计算模拟值与试验吻合较好.说明采用文献[8]的方法来计算凝胶和开裂应变的方法是合理的.在该算例中，由于无徐变影响，自生收缩值较小，模拟1和模拟2的结果十分接近.

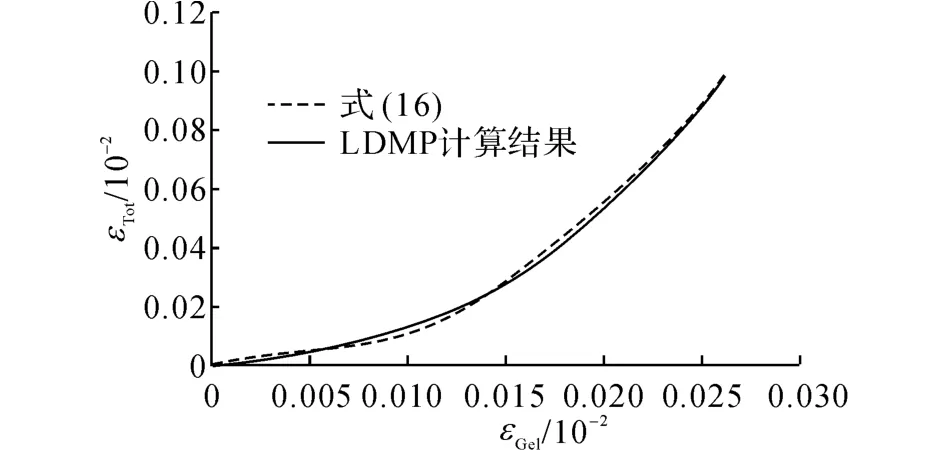
图6 η（εGel）表达式的确定Fig.6 Determination ofη（εGel）

用轴向承受10 MPa的3 mm厚钢环约束试件（三向受力状态）的轴向应变测量值来标定σmax.为了模拟试验中钢环与混凝土之间的相互作用，采用ABAQUS中的接触功能，两者切向定义为无摩擦.在模拟2中运用最小二乘法可得σmax=-7 MPa，模拟结果与试验值的比较如图7（e）所示.对比模拟1和2可以看出，在该试验中徐变和收缩效应是不可忽略的，它抵消了ASR膨胀应变，使得试件轴向发生收缩.

2.4 模型验证

采用上文标定的参数（cN=0.4，cD=cV=0.009，cE=0.001 7，σmax=-7 MPa）对Multon剩余的试验[2]进行模拟来验证本文模型.轴向应变及径向应变εr的模拟结果分别如图7（b）～（d）、7（f）～（i）及图8所示.可以看出，模拟2的结果与试验值吻合度较高，说明本文模型的计算方法是合理的.

分析模拟1的曲线可以发现：对于无约束试件（见图7（a）～（c）、8（a）～（c）中的模拟1曲线），当施加轴向荷载时，大部分ASR膨胀都发生在径向，而轴向ASR膨胀接近于零，甚至在20 MPa时变为收缩；当有钢环约束时，约束越强，轴向变形越大，径向变形越小.此外，比较模拟1和模拟2可知，当施加轴向荷载时，徐变和收缩占主导作用，使得总体轴向发生收缩.

3 结 语

本文提出适于分析ASR作用下混凝土力学行为的微平面模型.修改了微平面应力边界和法向模量的表达式，引入应力效应函数来模拟应力对ASR膨胀应变的影响.运用该模型对ASR作用下多种应力状态混凝土试件的力学行为进行模拟，计算值与试验值吻合良好，说明该模型可以推广应用于遭受ASR损害的混凝土结构分析.

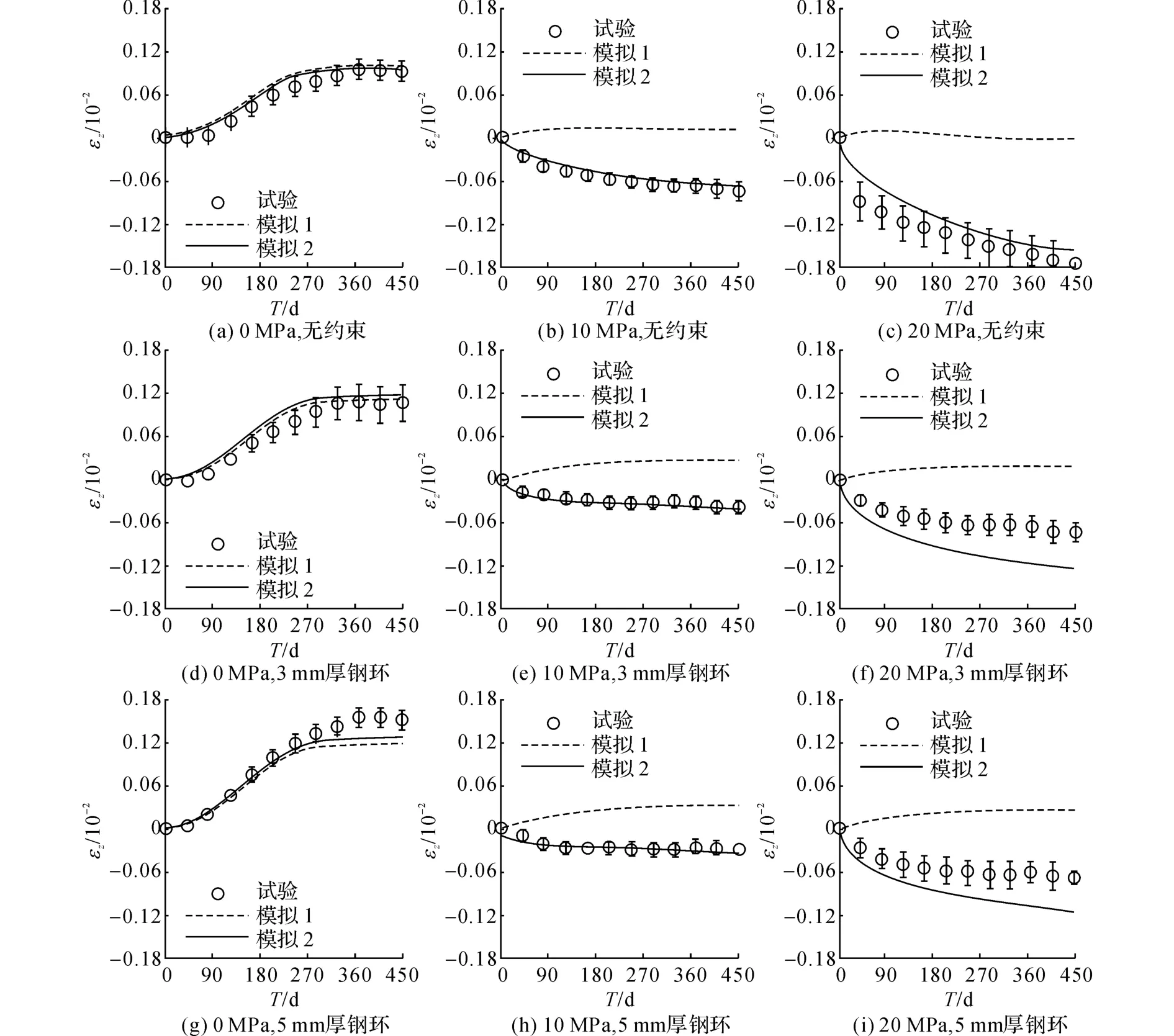
图7 轴向应变随龄期的变化历程Fig.7 Axial strain evolution with time

（

）：

[1]GIACCIO G，ZERBINO R，PONCE J M，et al.Mechanical behavior of concretes damaged by alkali-silica reaction[J].Cement and Concrete Research，2008，38（7）：993-1004.

[2]MULTON S，TOUTLEMONDE F.Effect of applied stresses on alkali-silica reaction-induced expansions[J].Cement and Concrete Research，2006，36（5）：912-920.

[3]PIETRUSZCZAK S.On the mechanical behavior of concrete subjected to alkali-aggregate reaction[J].Computers and Structures，1996，58（6）：1093-1097.

[4]BAZANT Z P，OH B H.Microplane model for progressive fracture of concrete and rock[J].Journal of Engineering Mechanics，1985，111（4）：559-582.

[5]CANER F，BAZANT Z P.Microplane model M7 for plain concrete.I：formulation[J].Journal of Engineering Mechanics，2013，139（12）：1714-1723.

[6]CANER F，BAZANT Z P.Microplane model M7 for plain concrete.II：calibration and verification[J].Journal of Engineering Mechanics，2013，139（12）：1724-1735.

[7]贾明晓，王君杰.微平面模型取向与权重的改进计算方法[J].工程力学，2013，30（6）：54-59.

JIA Ming-xiao，WANG Jun-jie.An improved method to calculate orientation and weight in a microplane constitutive model[J].Engineering Mechanics，2013，30（6）：54-59.

[8]ALNAGGAR M，CUSATIS G，DI-LUZIO G.Lattice discrete particle modeling（LDPM）of alkali silica reaction（ASR）deterioration of concrete structures[J].Cement and Concrete Composites，2013，41（8）：45-59.

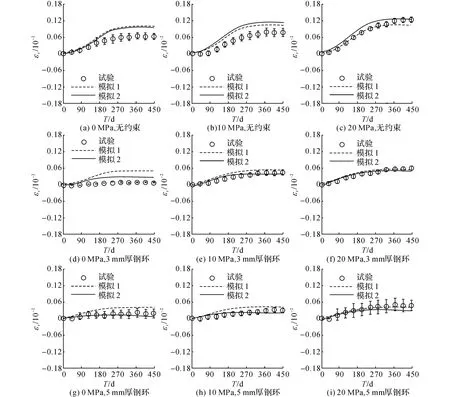
图8 径向应变随龄期的变化历程Fig.8 Radial strain evolution with time

[9]CUSATIS G，PELESSONE D，MENCARELLI A.Lattice discrete particle model（LDPM）for concrete failure behavior of concrete.I：theory[J].Cement and Concrete Composites，2011，33（9）：881-890.

[10]CUSATIS G，MENCARELLI A，PELESSONE D，et al.Lattice discrete particle model（LDPM）for failure behavior of concrete.II：calibration and validation[J].Cement and Concrete Composites，2011，33（9）：891-905.

[11]AHMED T，BURLEY E，RIGDEN S.The effect of alkali-silica reaction on the fatigue behaviour of plain concrete tested in compression，indirect tension and flexure[J].Magazine of Concrete Research，1999，51（6）：375-390.

[12]MULTON S，SEIGNOL J F，TOUTLEMONDE T.Structural behavior of concrete beams affected by alkali-silica reaction[J].ACI Materials Journal，2005，102（2）：67-76.

[13]BAZANT Z P，BAWEJA S.Creep and shrinkage prediction model for analysis and design of concrete structures：model B3[J].Materials and Structures，1995，28（6）：357-365.

Microplane modeling of ASR effects on concrete structures

DUAN An1，ZHANG Da-wei1，ALNAGGAR Mohammed2

（1.College of Civil Engineering and Architecture，Zhejiang University，Hangzhou 310058，China；2.Department of Civil and Environmental Engineering，Northwestern University，Evanston 60208，USA）

A modified microplane model was developed to simulate the alkali-silica reaction（ASR）damage based on the latest version of microplane theory M7 in order to accurately modeling the complicated behavior of concrete structures subjected to ASR.The material damage caused by the volume expansion of ASR gel was modeled in M7 as a reduction of material stiffness and boundaries.A stress effect function was proposed to depend on the normal stress of the microplane in order to consider the modification of ASR expansions due to applied stresses.The explicit algorithm for the model was established and implemented into commercial software ABAQUS.Finite element analysis of the ASR effect on laboratory specimens was conducted.The analytical results accorded with the experimental data.The validity of the proposed model was illustrated.

microplane theory；alkali-silica reaction（ASR）；concrete；ABAQUS

TU 528

A

1008-973X（2015）10-1939-07

2015-05-12.浙江大学学报（工学版）网址：www.journals.zju.edu.cn/eng

浙江省自然科学基金资助项目（LY14E080013）；中央高校基本科研业务费专项资金资助项目（2015FZA4019，2015FZA4018）；教育部留学回国人员科研启动基金资助项目.

段安（1982—），女，讲师，从事混凝土耐久性的研究.ORCID：0000-0002-0684-3872.E-mail：duanan09@zju.edu.cn

张大伟，男，副教授.ORCID：0000-0001-7838-6941.E-mail：dwzhang@zju.edu.cn