带关节约束的非冗余机械手臂二阶逆运动学控制

江 沛，黄水华，韦 巍，单才华，项 基

（1.浙江大学电气工程学院，浙江杭州310027；2.重庆大学机械传动国家重点实验室，重庆400030；3.浙江正特集团有限公司，浙江台州317004）

带关节约束的非冗余机械手臂二阶逆运动学控制

江 沛1，2，黄水华1，韦 巍1，单才华3，项 基1

（1.浙江大学电气工程学院，浙江杭州310027；2.重庆大学机械传动国家重点实验室，重庆400030；3.浙江正特集团有限公司，浙江台州317004）

针对关节限位和关节速度约束下的非冗余机械手臂控制问题，提出能够同时满足关节限位、关节速度约束的非冗余机械手臂二阶逆运动学算法.该算法将关节限位约束转换为带有时变阈值的关节速度约束，将时变阈值关节速度约束由真实关节空间映射到修正关节空间，变为固定阈值的关节速度约束；在修正关节空间通过加权最小二乘法，保证机械手臂运动过程中关节限位约束成立.该算法能够通过自适应调整权值矩阵满足关节速度约束，通过定理证明了该算法能够充分满足关节限位、关节速度约束.在三关节非冗余机械手臂上进行仿真实验，验证了该算法可以使闭环系统在实现轨迹跟踪的过程中保证关节限位、关节速度约束成立.

非冗余机械手臂；二阶逆运动学；关节限位约束；关节速度约束；修正关节；箝位任务

非冗余机械手臂是指关节数目等于机械手末端所在任务空间维度的机械手臂.由于非冗余机械手臂具有实现机械手臂末端任务的最小自由度，易于通过较小计算量实现较高精度的末端轨迹跟踪的特点，广泛应用于工业生产中.

实现机械手臂末端对目标轨迹跟踪最典型的方法是利用雅克比矩阵的伪逆求解从任务空间到关节空间的逆运动学变换，从而生成适当的电机运动指令[1-2].通过该方法可以在一阶逆运动学层面求解关节指令速度[3-4]以及二阶逆运动学求解关节指令加速度[5-8].

在机械手臂控制中通常需要考虑关节限位、关节速度等约束，若这些约束不能满足，则有可能对机械手臂造成机械结构上的损坏.在如何适度牺牲系统跟踪精度以满足机械手臂的关节约束方面，近20年取得了很多成果.Chan等[9]提出加权最小二乘法（WLN），通过改变关节权重，抑制相应的关节运动，从而满足关节限位约束.Huang等[10]提出在加权最小二乘法的基础上，加入关节箝位任务，从而加速关节退出关节限位的箝位加权最小二乘法（CWLN）.Xiang等[11]提出变权重加权方法，在适当牺牲跟踪误差的前提下，实现了关节限位避免及机械手臂避障.以上方法都是在一阶逆运动学层面求解关节指令速度，难以满足关节速度的约束.

Kircanski等[12]提出的算法可以在一阶逆运动学层面通过减小任务空间的期望速度，保证关节指令速度满足最大关节速度约束，而该算法可以推广到二阶逆运动学情形满足最大关节加速度约束.该方法存在以下2个问题：1）机械手臂不能在指定的时间内完成对期望轨迹的跟踪；2）机械手臂末端轨迹和期望的轨迹存在较大的误差.Antonelli等[13]在此基础上提出时间尺度概念，即在关节最大速度、最大加速度约束不满足时，通过改变时间尺度，对任务空间轨迹在时间维度上进行局部放缩，从而保证关节最大速度、加速度约束，并且实现对机械手臂末端期望轨迹的跟踪.Bianco等[14-15]将变时间尺度算法拓展到高维约束的情形，并引入动力学模型，解决了带有力矩约束的逆运动学问题.以上几种方法均不能在指定时间内实现对任务空间曲线的跟踪，在二阶（高阶）逆运动学层面上时间尺度放缩只能满足电机输出能力有限造成的最大关节速度、加速度约束，难以满足关节限位约束.

本文提出在关节限位及关节速度约束下的非冗余机械手臂二阶逆运动学算法，求解关节指令加速度.由于加速度控制不易满足关节限位约束，将关节限位约束转换为带有时变阈值的关节速度约束.时变阈值的逆运动学问题无法采用加权最小二乘法求解，本文提出修正关节概念.通过时变非齐次变换，将关节空间映射到修正关节空间.在修正关节空间，时变阈值的关节速度约束转换为定常阈值的修正关节速度约束，根据加权最小二乘法进行求解.在此基础上，对该控制算法进行拓展，使之能够同时满足关节限位约束和关节速度约束，进一步证明了在该算法下闭环系统满足约束，最后通过仿真验证了该算法的有效性.

1 二阶逆运动学控制

机械手臂正向运动学可以用如下形式表示：

式中：q为n维机械手臂关节位置矢量，x为末端执行器位置在任务空间的m维矢量表示，对于非冗余机械手臂，m=n；f（·）为非线性正向运动学函数.将式（1）对时间求导，可以得到一阶运动学方程：

式中：J为雅克比矩阵，J=∂f/∂q.对时间求导，可得二阶运动学方程如下：

已知执行器末端期望位置xd、期望速度˙xd、期望加速度¨xd，求解对应的关节加速度实现目标跟踪，可以通过基于伪逆的闭环逆运动学算法（CLIK）得到关节加速度指令：

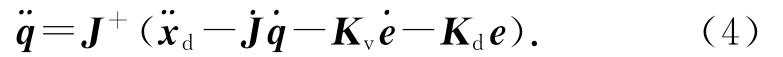
式中：e为末端执行器跟踪误差，e=x-xd；Ke、Kv为反馈增益矩阵，可以通过选择适当的Ke、Kv，并引入误差反馈使得e收敛.

2 带关节限位约束的二阶逆运动学控制

2.1 关节限位在关节速度层面的表述机械手臂物理关节限位可以表示为

式中：qi为机械手臂关节i的关节位置为机械手臂关节i的正、负限位.对于二阶逆运动学控制，常常需要将关节位置层面的关节限位约束转化到关节速度层面约束，本文给出连续系统关节限位约束在关节速度层面的表示如下：

式中：c为大于0的常数，˙qi为关节i的关节速度.为了探究式（5）、（6）之间的关系，给出如下定理.

定理1t0时刻，i=1，…，n且满足-qi（t））≤（t）≤c（-qi（t）），t∈，t∈[t0，t1].

由定理1可知，在连续系统中，式（6）为约束（5）成立的充分条件.根据定理1，可以将机械手臂的关节限位约束（5）转化为关节速度约束（6）.对于离散系统，定理1将不再成立，在离散系统中，关节限位约束将关节限位表示为增量形式：

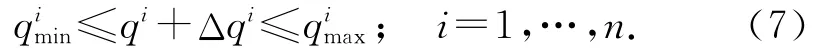
式中：Δqi为机械手臂第i个关节在无穷小时间Δt内关节位置的增量.将式（7）除以时间Δt，有

则有

其中c1=1/Δt.对于离散系统只需满足c1≤1/T，则可以保证关节限位约束成立，且离散系统约束（9）与连续系统约束（6）具有相同的形式.

2.2 带关节限位约束的二阶逆运动学控制算法

关节速度约束（6）的阈值中包含关节位置变量q，为时变阈值的关节速度约束，无法采用WLN方法求解.需要寻找一个非齐次映射，将关节空间速度映射到该空间中，并使关节速度约束（6）在该空间的表达式为恒定阈值，从而采用WLN方法求解.本文提出修正关节概念，真实关节空间通过如下变换将真实关节空间映射到修正关节空间：

式中：ε1为关节避障区域宽度，ε1＞0.当修正关节速度接近修正关节速度阈值时，通过减小相应的关节权重，将抑制修正关节速度的进一步变化.当修正关节速度远离修正关节速度限位时，通过调整权重移除对相应关节的运动限制，从而保证修正关节速度约束.

对式（10）进行微分并代入式（13），可以得到真实关节空间闭环控制律：

将式（15）代入式（3），可得系统误差方程：

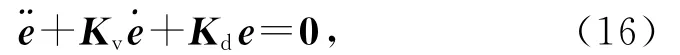
系统误差二阶指数收敛.

对于非冗余机械手臂，当关节限位触发时，W1将会出现缺秩，在雅克比矩阵处于非奇异位型的情况下，仍然可能引入算法奇异，使JW1JT不满秩，利用式（15）得到的关节加速度将趋于无穷大，超出电机的有效输出范围.为了解决机械手臂处于雅克比近奇异位型或算法近奇异位型，关节加速度过大的问题，引入带阻尼项的闭环控制律：

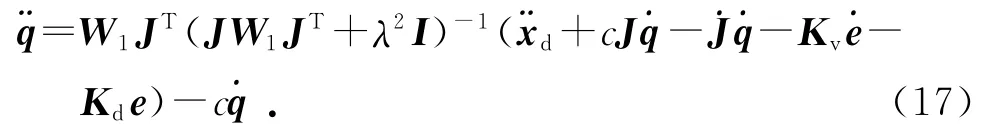
式中：λ为阻尼系数，λ≥0.较小的λ值系统有较高的准确性，但在近奇异位型下鲁棒性较差；较大的λ值系统有较好的鲁棒性，但会增加系统误差.本文使用Caccavale等[7]采用的方式设置阻尼项λ：

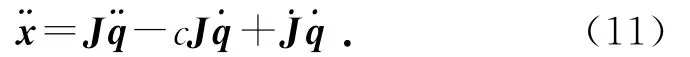
将式（10）代入时变阈值关节速度约束（6），可以得到修正关节速度约束：

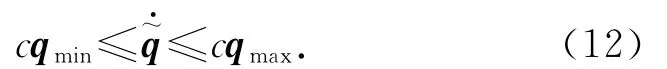
当真实关节在真实关节空间运动实现对期望轨迹的跟踪时，相应的修正关节在修正关节空间运动实现对相同轨迹的跟踪.当修正关节满足约束（12），则在真实关节空间约束（6）成立.在真实关节空间中，带有时变阈值关节速度约束（6）的逆运动学问题被转换为求解修正关节空间中带有固定阈值关节速度约束（12）的逆运动学问题.该问题可以通过WLN方法进行求解[9].闭环二阶逆运动学解为

式中：W1∈Rn×n为对角权值矩阵.采用文献[10]的方法设置加权矩阵如下：

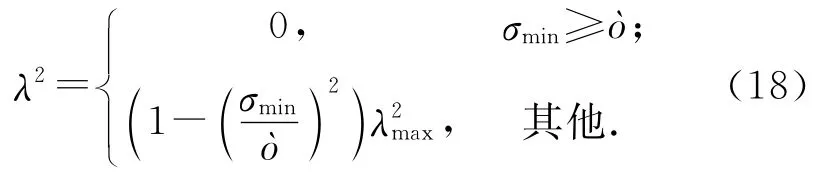
式中：σmin为的最小奇异值，ò为奇异避障区域宽度，λmax为最大阻尼常数.

3 带关节速度约束的二阶逆运动学控制

关节速度约束可以表示为

式中：W2为对角加值矩阵，

其中，ε2为关节速度避障区域宽度.利用式（20）得到的关节加速度由2部分组成.第一项是通过加权最小二乘法求得的相应的关节加速度，当关节速度接近关节速度阈值时，通过调整加权矩阵W2的值，使第一项关节加速逐渐趋向于0；当关节速度远离速度阈值，则移除对关节速度变化的抑制.第二项加速度分量为-，其方向与当前关节速度方向相反，将加速关节速度远离关节速度阈值，从而保证关节速度约束.

注解1式（17）为修正关节空间加权最小二乘法的二阶逆运动学解，与CWLN方法的逆运动学解有相似的形式.在关节限位约束下，关节限位约束等价于具有时变阈值的等价关节速度约束（6），式（17）可以看作通过设置关节箝位任务-，保证真实关节速度达到c）时，真实关节速度具有和等价关节速度阈值相同的变化率.关节速度约束（19）中的速度阈值固定，式（20）可以看作一阶CWLN方法在二阶逆运动学上的推广.式（20）中的关节箝位任务-的主要作用是加速关节速度离开关节速度限位.

4 同时具有关节速度和关节限位约束的二阶逆运动学控制

同时具有关节限位约束和关节速度约束的二阶闭环逆运动学问题可以描述为如下形式：

关节限位约束二阶闭环逆运动学解（17）和关节速度约束的闭环逆运动学解（20）具有统一形式，通过适当调整权值矩阵，可得同时满足关节限位约束和关节速度约束的闭环系统关节加速度解：

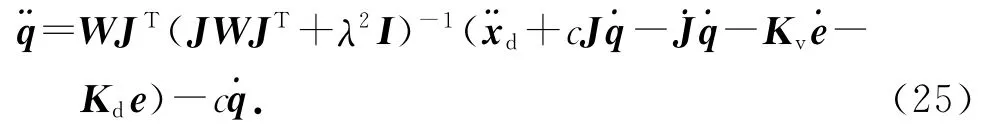
式中：W为对角权值矩阵，其对角元素定义为W（i，i）=min（W1（i，i），W2（i，i））；i=1，…，n.

为了能够在JW1JT缺秩的情况下得到可行关节加速度，在求解过程中加入了阻尼项，这可能导致约束不满足.进一步探讨在控制律（25）下，闭环系统对约束的满足情况.

定理2控制律（25）满足机械手臂关节限位约束（23）和关节速度约束（24）.

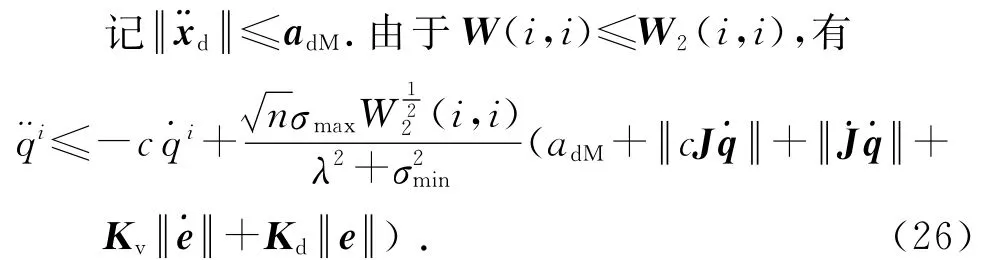
式中：σmin、σmax分别为JW1/2的最小、最大奇异值.当时，W2（i，i）=0，根据式（26），此时有＜0，与假设矛盾，故成立.同理可以证明，进而可以证明.

注解2式（25）为关节限位和关节速度约束下的非冗余机械手臂二阶逆运动学解.对于冗余机械手臂的二阶逆运动学求解，由于冗余机械手臂存在雅克比矩阵零空间中的关节自运动，二阶逆运动求解过程中通常出现解不稳定的情况[5，17].为了使控制律稳定，通常采用抑制雅克比零空间速度分量的方法[6]，而采用式（25）的加权方法无法完全实现对零空间速度分量的抑制，因而无法实现将其直接推广的冗余机械手臂的情形.

注解3在实际应用中，应注意常数c数值的选取.较大的c值能够在关节速度限位触发时，加速关节速度远离速度约束阈值；但是较大的c值会在限位触发时引入较大的误差.

5 实验结果

为了验证控制算法满足关节限位、关节速度约束的有效性，设计机械手臂在关节限位、关节加速度约束下跟踪任务空间目标曲线的仿真实验.仿真实验以7关节乒乓球机器人为模型，由于研究对象为非冗余机械手臂，而任务空间曲线为三维空间曲线.取乒乓球机械臂靠近基座的3个旋转关节串联组成的非冗余机械臂，如图1所示.图中，Z1、Z2、Z3分别为关节1～3的旋转轴.机械臂DH参数α、a、d如表1所示.关节限位qmin、qmax及关节速度阈值、如表2所示.机械臂初始关节位型q（0）= [2.174，2.426，3.042]T.机械臂末端在第三关节坐标系下的位置坐标为[100，180.9，0]T.系统采样周期T=0.005 s.

首先采用式（4）求解关节加速，其中Kd=20，Kv=10.仿真结果如图2、3所示.图中，e为跟踪误差.关节运动曲线较平滑，系统跟踪误差小于0.08 mm.式（4）无法保证关节位置约束.当t=5 s时，关节1位置超过正向关节限位.

表1 机械臂DH参数Tab.1 DH prameters of manipulator

表2 机械臂关节位置、速度阈值Tab.2 Joint position and velocity threshold of manipulator

图1 机械臂仿真模型Fig.1 Manipulator simulation model

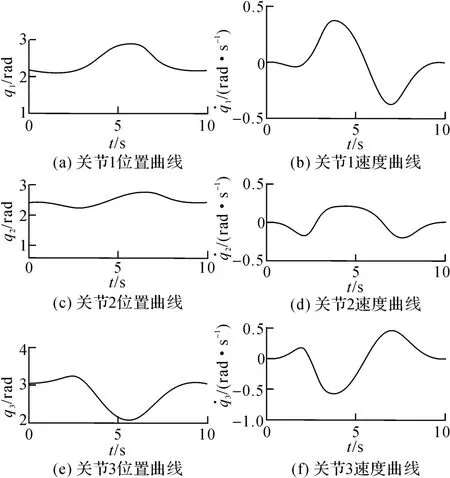
图2 关节位置及关节速度曲线Fig.2 Joint position trajectories and joint velocity trajectories

为了在跟踪任务空间轨迹的同时能够满足关节限位、关节速度约束，采用式（25）求解关节加速度，反馈增益系数设定同上.设定时间常数c=100≤1/T.关节避障区域宽度常数ε1=0.003，关节速度避障区域宽度系数ε2=0.15.采用文献[10]的方法设置λmax，ò如下：

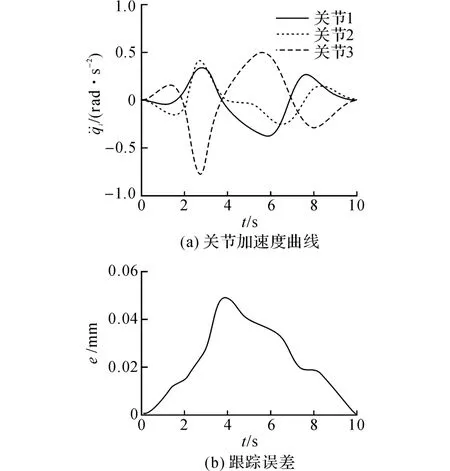
图3 关节加速度曲线和跟踪误差Fig.3 Joint acceleration trajectory and tracking error

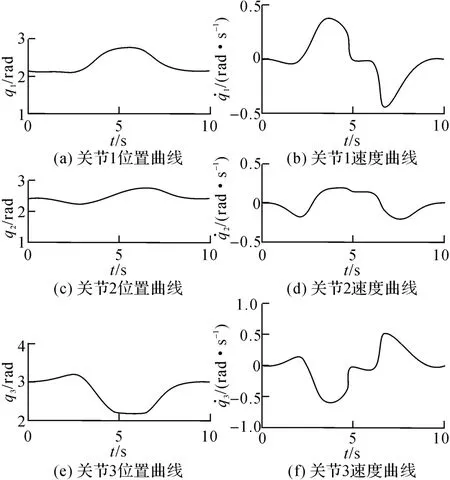
图4 关节位置及关节速度曲线Fig.4 Joint position trajectories and joint velocity trajectories

仿真结果如图4～6所示.图5中，W1（1，1）、W2（1，1）分别为关节1的位置权重和速度权重.在[0，4.8]s时间段，关节位置和关节速度远离约束限位，加权矩阵W=I，λ=0.在t=4.8 s，真实关节1靠近正向限位，对应的修正关节1的关节速度接近修正关节速度限位，如图6（b）所示.通过式（14）减小修正关节1的权重系数，使修正关节加速度迅速减小到0，阻止突破修正关节速度阈值.此时，修正关节1对应的真实关节速度被抑制到零，如图6（c）所示，成功实现了真实关节的关节限位避障.随着机械手臂的运动，1号关节速度反向并逐渐增大，当t=6 s时实际关节1开始反向退出关节正向限位，并在t=6.4 s时触发负向速度约束，通过式（21）减小关节速度权重W2（1，1）；在t=6.9 s，W2（1，1）＜W1（1，1），关节速度约束成为抑制1号关节运动的主要因素.与关节位置约束相比，关节速度能够更迅速地离开速度阈值，这是由于关节限位约束是在修正关节空间通过加权最小二乘法实现的，而关节速度约束是在真实关节空间通过CWLN方法实现的.CWLN方法中的关节箝位任务可以加速推动关节速度离开关节约束阈值[10].

图5 控制律（25）下的仿真结果Fig.5 Results of simulation under control law（25）

在关节限位、速度约束触发过程中，JWJT出现缺秩，最小奇异值减小到3.07×10-4，小于ò.通过设定λ，如图5（d）所示，保证了求解加速度有界，但阻尼项的加入使系统跟踪误差增大到15 mm.从t=7.8 s后，关节位置和关节速度均远离阈值，λ减小为0，跟踪误差逐渐减小到0.35 mm.

图6 关节加速度曲线及修正关节运动曲线Fig.6 Joint acceleration trajectories and revised joint motion trajectories

仿真实验在Matlab环境下执行，控制周期T=0.005 s，仿真任务持续时间为10 s.计算时间如表3所示.本文提出的控制律（25）与常用的基于伪逆的控制律（4）相比，未明显增加运算时间，控制周期的平均计算时间低于控制周期；在实际应用中，计算效率高于Matlab，因此该控制律能够运用于实时性较高的应用领域.

表3 曲线跟踪仿真实验的计算时间Tab.3 Computing time of curve tracking simulation

6 结 语

本文提出能够同时满足关节限位、关节速度约束的非冗余机械手臂二阶逆运动学算法.该算法将关节限位约束转换为带有时变阈值的关节速度约束，并将该约束由真实关节空间映射到修正关节空间，在修正关节空间通过加权最小二乘法保证关节限位约束；同时，能够通过调整权值，在真实关节空间中保证关节速度约束.本文进一步证明了采用该算法能够使关节限位、关节速度约束充分满足，并在三关节非冗余机械手臂上进行仿真实验.实验结果表明，采用该算法能够在跟踪目标曲线的同时，满足关节限位约束和关节速度约束，而较小的计算量使该算法能够应用于实时性较高的引用领域.

（

）：

[1]WHITNEYD E.Resolved motion rate control of manipulators and human prostheses[J].IEEE Transactions Human-Machine Systems，1969，10（2）：47-53.

[2]LIEGEOIS A.Automatic supervisory control of the configuration and behavior of multibody mechanisms[J].IEEE Transactions on Systems，Man and Cybernetics，1977，7（12）：868-871.

[3]NAKAMURA Y，HANAFUSA H.Optimal redundancy control of robot manipulators[J].The International Journal of Robotics Research，1987，6（1）：32-42.

[4]姜宏超，刘士荣，张波涛.六自由度模块化机械臂的逆运动学分析[J].浙江大学学报：工学版，2010，44（7）：1348-1354.

JIANG Hong-chao，LIU Shi-rong，ZHANG Bo-tao.Inversekinematics analysis for 6 degree-of-freedom modular manipulator[J].Journal of Zhejiang University：Engineering Science，2010，44（7）：1348-1354.

[5]HOLLERBACH J M，KI S.Redundancy resolution of manipulators through torque optimization[J].IEEE Journal of Robotics and Automation，1987，3（4）：308-316.

[6]HSU P，MAUSER J，SASTRY S.Dynamic control of redundant manipulators[J].Journal of Robotic Systems，1989，6（2）：133-148.

[7]CACCAVALE F，CHIAVERINI S，SICILIANO B.Second-orderkinematic control of robot manipulators with Jacobian damped least-squares inverse：theory and experiments[J].IEEE/ASME Transactions on Mechatronics，1997，2（3）：188-194.

[8]GUO Dong-sheng，ZHANG Yu-nong.Acceleration-level inequality-based MAN scheme for obstacle avoidance of redundant robot manipulators[J].IEEE Transactions on Industrial Electronics，2014，61（12）：6903-6914.

[9]CHAN Tan-fung，DUBEY R V.A weighted least-norm solution based scheme for avoiding joint limits for redundant joint manipulators[J].IEEE Transactions on Robotics and Automation，1995，11（2）：286-292.

[10]HUANG Shui-hua，PENG Yong-gang，WEI Wei，et al.Clamping weighted least-norm method for the manipulatorkinematic control：avoiding joint limits [C]∥Proceedings of the 33th Chinese Control Conference.Nanjing：[s.n.]，2014：8309-8314.

[11]XIANG Ji，ZHONG Cong-wei，WEI Wei.A varied weights method for thekinematic control of redundant manipulators with multiple constraints[J].IEEE Transactions on Robotics，2012，28（2）：330-340.

[12]KIRCANSKI M，KIRCANSKI N.Resolved-rate and resolved-acceleration-based robot control in the presence of actuators’constraints[C]∥Proceedings of IEEE International Conference on Robotics and Automation.Albuquerque：IEEE，1997：235-240.

[13]ANTONELLI G，CHIAVERINI S，FUSCO G.A new on-line algorithm for inversekinematics of robot manipulators ensuring path tracking capability under joint limits[J].IEEE Transactions on Robotics and Automation，2003，19（1）：162-167.

[14]BIANCO C G L，GERELLI O.Online trajectory scaling for manipulators subject to high-orderkinematic and dynamic constraints[J].IEEE Transactions on Robotics and Automation，2011，27（6）：1144-1152.

[15]BIANCO C G L，GHILARDELLI F.Real-time planner in the operational space for the automatic handling ofkinematic constraints[J].IEEE Transactions on Automation Science and Engineering，2014，11（3）：730-739.

[16]KHALIL H K，GRIZZLE J W.Nonlinear systems [M].Upper Saddle River：Prentice hall，2002.

[17]O’NEIL K A.Divergence of linear acceleration-based redundancy resolution schemes[J].IEEE Transactions on Robotics and Automation，2002，18（4）：625-631.

Second-order inversekinematic control method for non-redundant manipulator with joint constraints

JIANG Pei1，2，HUANG Shui-hua1，WEI Wei1，SHAN Cai-hua3，XIANG Ji1

（1.College of Electrical Engineering，Zhejiang University，Hangzhou 310027，China；2.State Key Laboratory of Mechanical Transmission，Chongqing University，Chongqing 400030，China；3.Zhejiang Zhengte Group Limited Company，Taizhou 317004，China）

A second-order inversekinematic control algorithm was proposed in order to control nonredundant manipulator with both joint limit and joint velocity constraints.The joint limit constraint was converted into the joint velocity constraint with time variant thresholds.Then real joint space was mapped into the revised joint space，in which joint limit constraint can be guaranteed by the weighted least-norm method.The method can achieve joint velocity constraint by adjusting the weight factors.A further proof that the both joint limit constraint and joint velocity constraint can be guaranteed by the method.A simulation was conducted on a three-link non-redundant manipulator in order to track a predefined trajectory.Results demonstrated that the method successfully guaranteed both joint limit constraint and joint velocity constraint.

non-redundant robot manipulator；second-order inversekinematic；joint limit constraint；joint velocity constraint；revised joint；clamping task

TP241

A

1008-973X（2015）10-1885-08

2014-09-04.浙江大学学报（工学版）网址：www.journals.zju.edu.cn/eng

国家自然科学基金资助项目（61374174）；中央高校基本科研业务费专项资助项目（2013QNA4021）；新世纪优秀人才资助项目（NCET-11-0459）；浙江省“钱江人才”计划资助项目（2013R10047）；浙江省自然科学基金资助项目（LY13F030001）；杭州市产业链重大科技创新资助项目（20132111A04-2）.

江沛（1985—），男，博士生，从事机械手臂控制的研究.E-mail：denis-samurai@163.com

项基，男，教授，博导.E-mail：jxiang@zju.edu.cn