工业企业主要经济指标分析

陈斯祺

（东南大学机械工程学院，江苏 南京 211189）

新中国成立以来，我国工业产业迅猛发展，为整个社会的经济建设贡献着重要的力量。而地区工业企业的经济状况又关乎着发展水平和未来的分析决策。因此，工业企业的各项经济指标的分析就尤为重要。但是，现有的官方数据指标项目繁多，给后续分析带来困难。本文则针对工业企业主要经济指标，通过主成分分析的方法进行简化，为进一步研究工业企业经济发展做好数据工作。

1 数据来源

本文中所有数据均来自国家统计局官方网站。选取具有代表性的工业大省河北省为例，以该省2013年全年11个月度数据为样本，对国家统计局给出的分省月度数据工业企业主要经济指标中的全部52项指标数据进行分析。

2 主成份分析法（Principal Component Analysis,PCA）

主成份分析法也称主分量分析或矩阵数据分析,通过变量变换的方法把相关的变量变为若干不相关的综合指标变量。[1]

若某研究对象有两项指标 ζ1和 ζ2,从总体 ζ(ζ1,ζ2)中抽取了 N 个样品,它们散布在椭圆平面内(见图1),指标 ζ1与 ζ2有相关性。 η1和 η2分别是椭圆的长轴和短轴,η1⊥η2,故 η1与 η2互不相关。其中 η1是点 ζ(ζ1,ζ2)在长轴上的投影坐标,η2是该点在短轴上的投影坐标。从图1可以看出点的N个观测值的波动大部分可以归结为η1轴上投影点的波动,而η2轴上投影点的波动较小。若η1作为一个综台指标,则η1可较好地反映出N个观测值的变化情况,η2的作用次要。综合指标η1称为主成份,找出主成份的工作称为主成份分析[2]。

可见,主成份分析即选择恰当的投影方向,将高维空间的点投影到低维空间上,且使低维空间上的投影尽可能多地保存原空间的信息,就是要使低维空间上投影的方差尽可能地大[3]。

3 应用主成份分析法分析工业企业主要经济指标

3.1 数据处理

对所选原始数据进行标准化，利用SPSS软件进行主成分分析，得到解释的总方差（见表1）和成分矩阵（见表2）。

表1 各指标解释的总方差

表2 成份矩阵

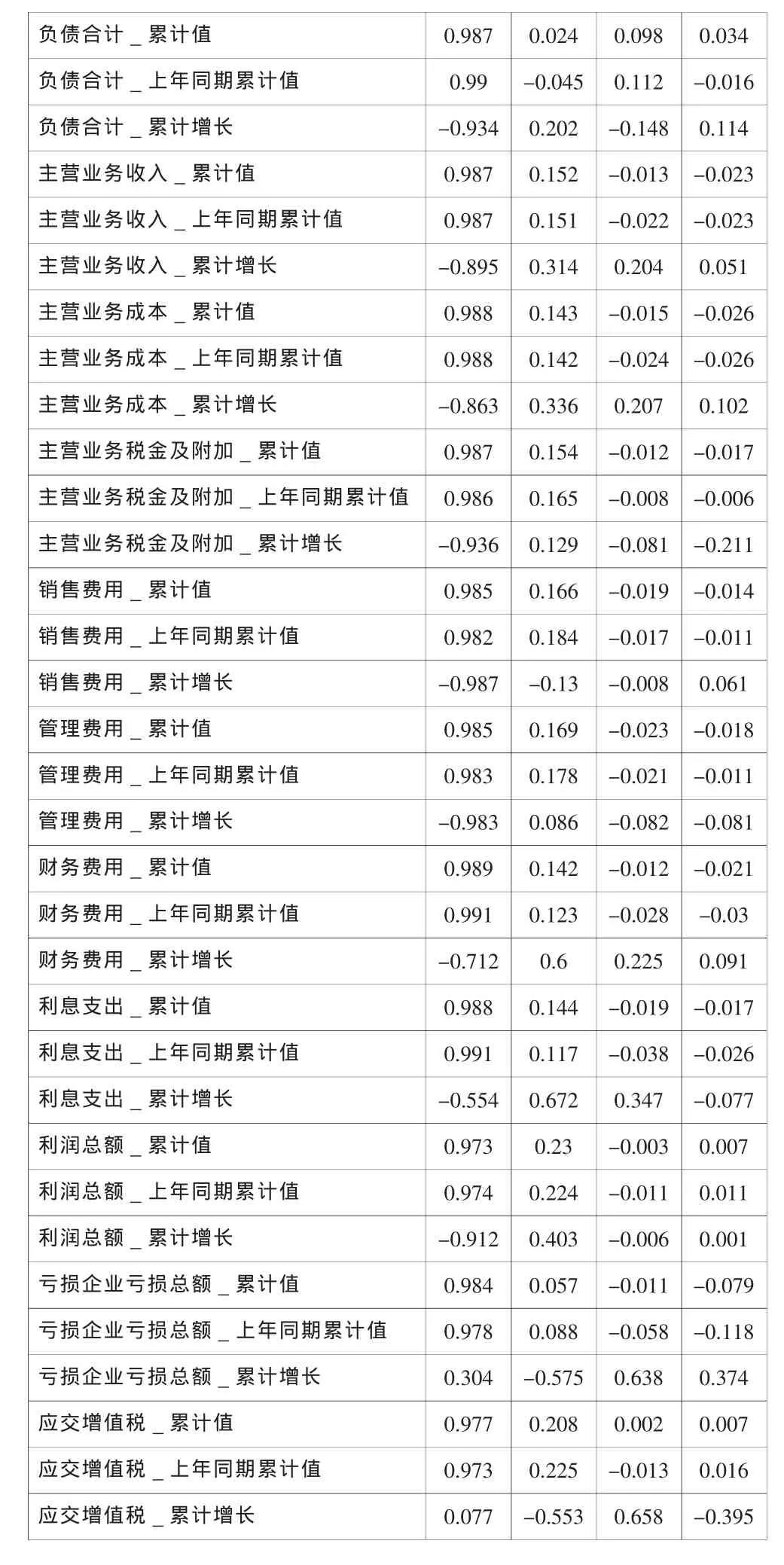
负债合计_累计值 0.987 0.024 0.098 0.034负债合计_上年同期累计值 0.99 -0.045 0.112 -0.016负债合计_累计增长 -0.934 0.202 -0.148 0.114主营业务收入_累计值 0.987 0.152 -0.013 -0.023主营业务收入_上年同期累计值 0.987 0.151 -0.022 -0.023主营业务收入_累计增长 -0.895 0.314 0.204 0.051主营业务成本_累计值 0.988 0.143 -0.015 -0.026主营业务成本_上年同期累计值 0.988 0.142 -0.024 -0.026主营业务成本_累计增长 -0.863 0.336 0.207 0.102主营业务税金及附加_累计值 0.987 0.154 -0.012 -0.017主营业务税金及附加_上年同期累计值 0.986 0.165 -0.008 -0.006主营业务税金及附加_累计增长 -0.936 0.129 -0.081 -0.211销售费用_累计值 0.985 0.166 -0.019 -0.014销售费用_上年同期累计值 0.982 0.184 -0.017 -0.011销售费用_累计增长 -0.987 -0.13 -0.008 0.061管理费用_累计值 0.985 0.169 -0.023 -0.018管理费用_上年同期累计值 0.983 0.178 -0.021 -0.011管理费用_累计增长 -0.983 0.086 -0.082 -0.081财务费用_累计值 0.989 0.142 -0.012 -0.021财务费用_上年同期累计值 0.991 0.123 -0.028 -0.03财务费用_累计增长 -0.712 0.6 0.225 0.091利息支出_累计值 0.988 0.144 -0.019 -0.017利息支出_上年同期累计值 0.991 0.117 -0.038 -0.026利息支出_累计增长 -0.554 0.672 0.347 -0.077利润总额_累计值 0.973 0.23 -0.003 0.007利润总额_上年同期累计值 0.974 0.224 -0.011 0.011利润总额_累计增长 -0.912 0.403 -0.006 0.001亏损企业亏损总额_累计值 0.984 0.057 -0.011 -0.079亏损企业亏损总额_上年同期累计值 0.978 0.088 -0.058 -0.118亏损企业亏损总额_累计增长 0.304 -0.575 0.638 0.374应交增值税_累计值 0.977 0.208 0.002 0.007应交增值税_上年同期累计值 0.973 0.225 -0.013 0.016应交增值税_累计增长 0.077 -0.553 0.658 -0.395

3.2 结果分析

由主成份分析的计算结果可以看出,原变量的方差在新变量中的集中度很高,根据工业企业主要经济指标的实际状况和主成份分析的要求,本文取前4个主成份来反映原来的52个变量,其方差的累计贡献率已达到96.008%,表明四个主成份在96.008%的程度上反应了地区工业企业主要经济状况。可以认为,这四个主成份基本上能够反映出原变量的变化所代表的工业企业经济指标情况。

4 结论

主成份分析法结果表明,地区工业企业主要经济指标可以分为四类：支出类指标,存货状况类指标，亏损类指标和流动资产类指标。四种新指标反映的情况与原所有指标反映的情况相近程度达96.008%,可以大大减少后续工作量。主成份分析法是分析工业企业主要经济指标的一种很好的工具,其分析结果对分析地区工业企业经济状况做出合理决策具有指导作用。

［1］汪应洛.系统工程[M].北京:机械工业出版社,2009:54-60.

［2］方开泰.实用多元统计分析[M].上海:华东师范大出版社,1989:291-302.

［3］王学仁,王松桂.实用多元统计分析[M].上海:上海科技出版社:1990,270-272.

［4］方开泰.实用多元统计分析[M].上海:华东师范大学出版社,1989:291-302.

［5］姜扬.聚类和主成分回归在经济指标数据中的应用研究[D].吉林大学,2010.