门式连续刚构桥上无缝线路纵向力计算方法研究

刘亚航，田德仓，丁静波

(中铁工程设计咨询集团有限公司轨道工程设计研究院，北京100055)

门式连续刚构桥上无缝线路纵向力计算方法研究

刘亚航，田德仓，丁静波

(中铁工程设计咨询集团有限公司轨道工程设计研究院，北京100055)

广州市轨道交通21号线高架桥为多跨门式连续刚构桥，桥上铺设无缝线路，传统纵向力计算模型复杂。为满足实际工程需要，以梁轨相互作用原理为基础将计算模型简化处理，建立钢轨、扣件、桥梁及墩台一体化的等效计算模型。计算对比表明，简化模型计算所得伸缩力、制动力及断缝值与传统模型计算值基本吻合，两者差异在可接受的范围以内，既保证了计算的准确性，又提高了计算速度。

门式连续刚构桥 桥上无缝线路 伸缩力 制动力 断缝

根据现有的城市轨道交通高架线路运营情况，刚构桥以其优越的特点被广泛使用，对降低桥上无缝线路钢轨伸缩力、制动力等都有较为明显的效果。广州地铁21号线采用地下线与高架线相结合的方式。其中，高架线采用了多跨门式连续刚构桥上无缝线路，充分利用了刚构梁的结构特点，既减小无缝线路温度跨度，又提高了线路基础的稳定性。

多跨门式连续刚构桥上无缝线路结构较为复杂，全段均属固定支点，梁体整体抗推刚度分配到每个墩台误差大，计算模型建立过程复杂，不利于快速解决工程问题。本文根据实际需要，通过对桥上无缝线路梁轨相互作用的剖析，简化该桥型无缝线路计算模型，以实现快速准确地检算的目的。

1 门式连续刚构桥上无缝线路特征

门式连续刚构桥以传统的连续刚构桥型为基础，将连续桥中所有支点都设置成固结，使整个梁体形成一个整体受力系统，通过梁体的整体抗推刚度抵抗外部纵向作用力。连续的门式刚构桥(图1)桥面连续性好，行车平顺，梁体的内力分布更加合理，减小了无缝线路的温度跨度，有效地降低了钢轨所受的附加应力，对于桥上无缝线路钢轨的强度和稳定性起到了有利的作用。

图1 门式连续刚构桥示意

由于门式连续刚构桥不设置活动支座，不利于梁体内部温度力的自由释放，因此，为了减小桥梁自身内部受力，相比于普通的连续刚构桥，该桥型的桥墩以桥跨中部为中心对称布置，且墩台刚度设计普遍偏小。这样降低了每个固定墩对于梁体伸缩的约束力，特别是边跨墩与中间跨墩的截面惯性矩比值为1∶6.5左右，允许边跨梁体进行适当的伸缩，可在保证梁体整体结构稳定的前提下，同时又使得梁体内部受力得以有效释放。

2 计算模型及参数

以广州市轨道交通21号线高架线桥上无缝线路为算例，建立传统型和简化型两种模型进行对比分析，验证简化模型计算的准确性。

2.1 计算工况介绍

广州市轨道交通21号高架线为混凝土多跨门式连续刚构桥，铺设桥上无缝线路。由于高架段较长，取中间部分桥跨作为算例。所取桥梁全长412 m，梁跨布置为3×37 m连续刚构梁+(58+95+58)m连续刚构梁+2×30 m连续刚构梁+30 m刚构梁，梁轨相对布置如图2所示。

主要设计参数:线路设计时速120 km/h，铺设无砟轨道;钢轨采用60 kg/m无螺栓孔新轨，材质为U75V;WJ-2A型扣件，轨枕间距600 mm;最高轨温59.1℃，最低轨温0℃，设计锁定轨温(33±5)℃，无砟轨道与混凝土梁的日温差30℃;机车类型采用B型列车系列。

2.2 门式连续刚构桥上无缝线路计算模型简化

1)传统计算模型

根据梁轨相互作用原理，计算模型采用杆单元模拟钢轨，非线性的弹簧单元k1模拟线路纵向阻力，梁单元模拟桥梁梁体，并用线性的弹簧单元k2i模拟桥梁的水平线刚度对梁轨作用的影响。

根据梁轨相互作用的力学原理，对工况中所例举的桥上无缝线路进行模拟计算。其中k1取扣件的线路纵向阻力值;k2i为墩台纵向水平刚度，由于门式连续刚构桥的纵向水平刚度为梁的整体抗推刚度，需要根据每个墩的截面特性进行单个墩台纵向水平刚度重分配，考虑到边跨墩与中间跨墩的截面惯性矩比值为1∶6.5，将梁体的抗推刚度按照墩身截面惯性矩比值对每个墩进行分配，以求得每个墩的纵向水平模拟刚度值{k21，k22，…，k2i}。

根据线路计算参数，建立如图3的多跨门式连续刚构桥上无缝线路计算模型。模型依据实际设计的梁轨相对布置关系而建立，与设计结构保持一致。但是，在墩台纵向水平刚度取值中运用了分配法，造成参数输入具有一定的误差，给计算结果带来影响，同时由于模型中存在较多的固定支座，即增加了误差累计的不利因素;加之在建立模型和计算的过程中花费了较多的时间，不利于快速有效地为设计工作提供结果文件。为此，考虑该种桥上无缝线路结构上的特殊性，根据梁轨相互作用原理，在保证计算结果准确性的前提下，将模型进行简化。

2)简化计算模型

图2 21号线多跨门式连续刚构桥上无缝线路布置(单位:m)

图3 多跨门式连续刚构桥上无缝线路计算模型

简化计算模型的主要思路是在保持传统的梁轨相互作用基本原理不变的前提下，对梁体的纵向水平刚度模拟进行简化。多跨门式连续刚构桥的主要特点就是墩台刚度取值普遍较小，特别是边跨墩，对于梁端钢轨和梁体的伸缩位移约束力十分有限;并且该梁体的墩台设计以梁跨中部为中心对称布置。因此，可根据梁轨相互作用的关系，将模型进行简化处理。

对于该桥型，考虑到桥上无缝线路的基本假设“桥梁固定支座能完全阻止梁体的伸缩，不计活动支座对梁体纵向位移的影响”，既然边跨墩无法约束梁体纵向位移，在模型中就可将其等效为活动支座;同时，由于墩台是以梁体跨中为中心对称布置，在温度、荷载作用下，梁体位移存在“零点”，就可将梁体的整体抗推刚度等效为设置在该“零点”位置的固定支座，这样模型就可等效转化为单固定支座的简单结构。梁体纵向水平刚度等效变化如图4所示。

图4 门式连续刚构桥简化计算模型

模型等效简化过程中，桥跨长L11+L22=L1+L2+ L1，抗推刚度k2=k21+k22+k23+k24，简化模型既有效缩减了计算模型的模拟工作量，同时采用的是桥梁的整体抗推刚度，避免了刚度分配所带来的误差，使模拟计算更为简单有效。

3 计算模型对比分析

根据上述对桥上无缝线路模型的简化思路，分别计算伸缩力、制动力及断缝值，对两种模型计算结果进行对比分析。

3.1伸缩力

根据《铁路无缝线路设计规范》(TB 10015—2012)，伸缩力指桥梁与钢轨因温度变化产生的纵向相对位移引起的纵向力。考虑无砟轨道混凝土梁的日温差30℃，计算该桥梁工况伸缩力如图5、图6所示。

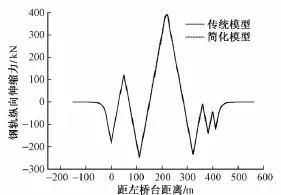
图5 降温时伸缩力对比

图6 升温时伸缩力对比

由图5、图6可以看出:在受到桥梁温度变化影响的情况下，由于梁体的伸缩造成钢轨与桥梁产生相对位移，进而使钢轨产生了纵向的伸缩力。根据图中对比可看出简化后的模型计算结果无论从变化规律还是从数值上都与传统模型相一致，伸缩力变化曲线基本重合在一起。两种模型计算结果对比见表1。

表1 两种模型伸缩力计算结果对比

通过对伸缩工况下不同位置的伸缩力进行比对分析，简化模型计算得出各处伸缩力变化率在1.5%范围以内，最大变化值1.7 kN。

简化模型中采用了梁体的整体抗推刚度作为单独固定支座的纵向水平刚度，可通过梁体在某个特定位置的纵向位移计算出与实际情况相对应的墩台纵向力。图7和图8为桥梁升、降温工况下两种模型计算所得墩台力的对比图。可见，除了7#墩墩台力计算差异略微偏大以外，其余墩台力计算值都具有一致性。7#墩墩台力差异性较大的原因为传统模型中该桥跨在墩台纵向水平刚度分配过程中出现误差，造成该处梁体位移与简化模型计算值有出入，由此也可以看出，简化模型直接跳过这个分配过程，有利于提高模型计算的准确性。

图7 降温时墩台力对比

图8 升温时墩台力对比

通过对伸缩工况下不同墩台的墩台力进行比对分析，简化模型计算得各墩台力变化率为0.8%～4.1%，最大变化值57.6 kN。

3.2 牵引(制动)力

根据《铁路无缝线路设计规范》(TB 10015—2012)，牵引(制动)力指因列车在桥梁上启动或制动，引起桥梁与钢轨纵向相对位移而产生的纵向力。考虑机车类型采用B型列车系列，8辆编组长度，计算该桥梁工况制动力如图9所示。

由图9可以看出:列车制动情况下，简化模型计算所得钢轨制动力变化规律与传统模型基本吻合，在跨中部分有一小段差异，考虑为墩台刚度分配不准确造成。两种模型计算结果对比见表2。

图9 制动力对比

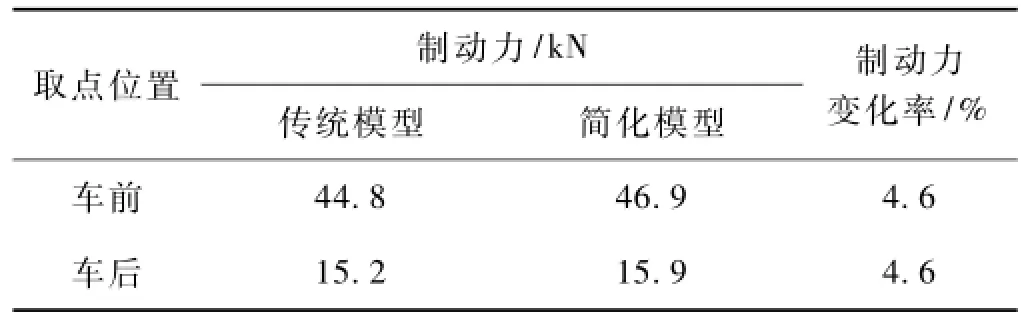
表2 两种模型制动力计算结果对比

3.3 断缝值

根据《铁路无缝线路设计规范》(TB 10015—2012)，桥上钢轨产生温度拉力和伸缩拉力，一旦钢轨折断，温度拉力和伸缩拉力按纵向阻力梯度放散，在钢轨折断处形成较大断缝。

图10为在断轨情况下两种模型计算所得钢轨位移曲线，进而可求得钢轨断缝值分别为60.8 mm和61.6 mm，断缝变化率为1.3%。

图10 断轨工况下断缝值

按照断缝公式λ=EF(αΔTdmax)2/r，求得断缝值为57.7 mm。计算值比有限元模型计算结果相对较小，分析原因为公式中未考虑桥上无缝线路附加力及墩台的线刚度等因素的影响。对于这种误差，都在工程计算的可接受范围之内。

4 结论

本文针对当前城市轨道交通建设中出现的新型多跨门式连续刚构桥上无缝线路的计算方法进行简化研究，简化方法主要依据桥梁的自身设计特点，具有一定的局限性。根据计算结果对比分析，得出以下结论:

1)多跨门式连续刚构桥采用全线固定支点结构，其纵向水平刚度为每个梁体的整体抗推刚度，传统的桥上无缝线路有限元计算需要对每个墩的纵向刚度进行重新分配，同时需要模拟大量的固定支座，不利于进行快速准确的工程计算。简化模型的提出有效地解决了这些问题。

2)根据桥上无缝线路设计对钢轨强度、线路稳定性及钢轨断缝的要求，分别从伸缩力、制动力及断缝值三方面对比简化模型与传统模型计算结果的差别，得出两种模型计算所得伸缩力最大差值1.7 kN;制动力最大差值2.1 kN;断缝值差值0.8 mm，与公式计算差值3.9 mm。可以看出两种模型计算值变化率均在5.0%以内。

3)对于墩台受力，对比两种模型计算结果，伸缩工况下墩台力最大差值57.6 kN;制动工况下墩台力最大差值5.2 kN。对于墩台受力，两种模型计算差值变化率也均在5.0%以内。

综上所述，简化计算模型能够较为快速、准确地实现多跨门式连续刚构桥上无缝线路设计检算的目标，其简化思路充分体现了桥上无缝线路梁轨相互作用的本质关系。

［1］张建.刚构桥上无缝线路的ANSYS分析及二次开发［D］.长沙:中南大学，2007.

［2］张永水，曹淑上.连续刚构桥薄壁墩抗推刚度计算方法研究［J］.中外公路，2006，26(6):144-145.

［3］魏涛.多跨连续刚构桥的设计参数分析及研究［D］.西安:长安大学，2010.

［4］中华人民共和国铁道部.TB 10015—2012铁路无缝线路设计规范［S］.北京:中国铁道出版社，2013.

［5］洪晓龙，吴仁义，张亚爽，等.温度作用下连续梁桥上CRTSⅡ型板板端宽裂缝对钢轨应力以及桥墩纵向力的影响研究［J］.铁道建筑，2013(6):135-138.

［6］孙井林，丁静波，李敏.上海地铁11号线(北段)无缝线路设计［J］.铁道标准设计，2010(5):14-15.

(责任审编孟庆伶)

U443.31+2

A

10.3969/j.issn.1003-1995.2015.06.34

1003-1995(2015)06-0132-04

2014-10-20;

2015-03-26

刘亚航(1987—)，男，河南新郑人，助理工程师，硕士。