煤矿开采沉陷中平均采深相关问题探讨∗
张新盈 王玉振
(河南水利与环境职业学院土木工程系,河南省郑州市,450008)
★煤炭科技·地质与勘探★
煤矿开采沉陷中平均采深相关问题探讨∗
张新盈 王玉振
(河南水利与环境职业学院土木工程系,河南省郑州市,450008)
针对开采沉陷实测数据处理时往往采用平均采深代替走向主断面实际采深的情况,首先在三种不同情况下分别求取采深偏移系数,并对其进行重新归类,而后对采深偏移系数与覆岩岩性、煤层倾角等因素之间关系进行探讨,最后推导了采深偏移系数对相关参数的影响。结果表明:采动程度对采深偏移系数无影响,覆岩强度和煤层倾角与采深偏移系数成正相关关系;采深偏移系数越大,则计算的主要影响半径与实际相差的越多。
采深偏移系数 松散层 主要影响半径 相对误差
矿山开采沉陷问题的核心内容是实测数据的处理和开采沉陷损害预计。而在开采沉陷实测数据处理时,往往会采用平均采深代替走向主断面实际采深进行相关沉陷计算,这会给结果带入一定的误差,甚至粗差。通过阅读资料发现,对用平均采深代替走向主断面实际采深所导致的问题进行研究的文献虽有,但对其深入研究的不多。本文通过相关公式的推导,对在开采沉陷中采深偏移系数的性质及其对相关参数的影响进行相关探讨。
1 采深偏移系数的求取
为了衡量采用平均采深代替走向主断面实际采深进行相关沉陷计算时产生的误差大小,令采深偏移系数p用下式表示:

式中:p——采深偏移系数;
H——实际采深,m;
H0——平均采深,m。
从倾向主断面上计算走向主断面的采深,参照采动程度和松散层厚度等因素可分为三种情况:非充分采动下,松散层厚度h小于0.1倍采深的情况,此时松散层可以忽略不计;非充分采动下,松散层厚度h大于0.1倍采深的情况;充分采动的情况。下面就这三种情况分别说明。
1.1 非充分采动下松散层厚度小于0.1倍采深的情况
当松散层厚度小于0.1倍采深时,松散层可以被视作同等厚度的基岩层。这种情况下的最大下沉角为最大下沉点在地面上的投影点与采空区中心的连线和水平线在下山一侧的夹角。此时走向主断面采深计算示意图如图1所示。
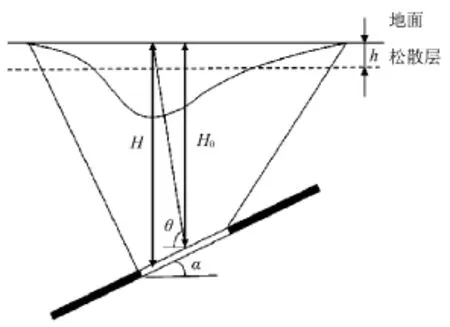
图1 非充分采动(不考虑松散层)走向主断面采深计算示意图
根据相关几何知识,求得非充分采动下松散层厚度小于0.1倍采深的情况下,走向主断面实际采深H如下式所示。

式中:α——煤层倾角,(°);
θ——最大下沉角,(°)。
则非充分采动下松散层厚度小于0.1倍采深的情况下的采深偏移系数为:

1.2 非充分采动下松散层厚度大于0.1倍采深的情况
根据文献,当松散层厚度大于0.1倍采深时,必须考虑松散层。这种情况下的最大下沉角可以被定义为最大下沉点在基岩面上的投影点和采空区中心的连线与水平线在下山方向上的夹角。此时的走向主断面采深计算示意图如图2所示。

图2 非充分采动(考虑松散层)走向主断面采深计算示意图
根据图2计算所得非充分采动下松散层厚度h大于0.1倍采深的情况下的走向主断面实际采深如下式所示:
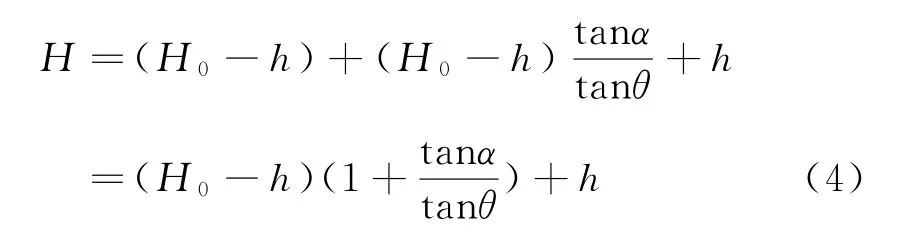
则相应的采深偏移系数为:

1.3 充分采动的情况
根据文献,在倾斜主断面达到充分采动的情况下,无论松散层厚度是否大于0.1倍的采深,都无需单独考虑松散层的地质条件。这种情况下的最大下沉角可以被定义为地表下沉盆地平底部分的两个边缘点在地面上的投影点与采空区上、下山边界连线的交点与采空区中心的连线和水平线在下山方向上的夹角。此时的走向主断面实际采深计算如图3所示。
根据图3计算所得的充分采动情况下,走向主断面实际采深如下式所示:
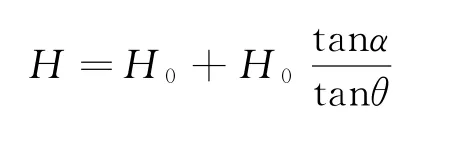


图3 充分采动下走向主断面采深计算示意图
则相应的采深偏移系数为:

1.4 重新分类
从式(3)和式(7)可以看出,非充分采动下松散层厚度小于0.1倍采深的情况和充分采动的情况两者所推导出的采深偏移系数完全一样。因此采动程度与采深偏移系数无关,可以将分类方法从同时考虑采动程度和松散层影响两种因素转变为只考虑松散否影响一种因素的分类方法。所以以上三种分类可以重新归结为两类:
(1)未考虑松散层影响的一类,其采深偏移系数为:

(2)考虑松散层影响的一类,其采深偏移系数为:

2 采深偏移系数随覆岩岩性和煤层倾角的变化
在煤层倾角小于50°并参考岩性的情况下,最大下沉角的计算经验公式为:

式中:k——岩石硬度系数。
当覆岩岩性为坚硬时,k取0.7~0.8;当覆岩岩性为中硬时,k取0.6~0.7;当覆岩岩性为软弱时,k取0.5~0.6。
将式(10)带入式(8),则得:

当k为不同取值时,采深偏移系数随倾角的变化关系如图4所示。

图4 不同k值时采深偏移系数随倾角的变化关系示意图
从图4可以看出,在煤层倾角相同的情况下,覆岩岩性越硬,采深偏移系数越大;而在覆岩岩性相同的情况下,煤层倾角越大,采深偏移系数越大。
3 采深偏移系数对相关沉陷参数的影响
3.1 采深偏移系数对角量参数的影响
开采沉陷中主要有边界角、移动角、裂缝角、充分采动角、最大下沉角等角量参数。与采深偏移系数相关的主要有边界角、移动角、裂缝角等。采深偏移系数对角量参数的影响主要体现在边界角δ0、移动角δ″和裂缝角δ的求取上。相关角量参数的求取如图5所示,其中ø松散层移动角。
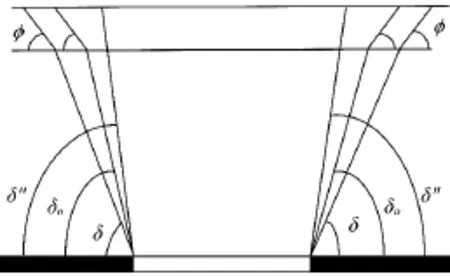
图5 角量参数求取示意图
以乌兰木伦矿为例,将其地质条件简化为松散层厚度20 m,平均采深100 m,盆地下沉10 mm边界点到采空区边界上方的距离为50 m,盆地临界变形值点到采空区边界上方的距离为45 m,盆地最外裂缝点到采空区边界上方的距离为30 m,松散层移动角为45°。边界角δ0主要是采用盆地主断面上下沉10 mm的点来划定移动盆地的最外边界,由最外边界的边界点用松散层移动角画线与基岩和松散层交界面相交,此交点至采空区边界的连线与水平线在煤柱一侧的夹角即为边界角;移动角δ主要采用盆地主断面上临界变形值来划定移动盆地的危险移动边界,由危险移动边界的临界变形点用松散层移动角画线与基岩和松散层交界面相交,此交点至采空区边界的连线与水平线在煤柱一侧的夹角即为移动角;而裂缝角δ″采用盆地主断面上最外侧的裂缝来圈定裂缝边界,由裂缝边界点至采空区边界的连线与水平线在煤柱一侧的夹角即为裂缝角。则根据不同采深偏移系数计算出来的角值如表1所示。

表1 角值随采深偏移系数变化表

表2 角值相对误差随采深偏移系数变化表
从表1和表2可以看出,在求取走向边界角、走向移动角和走向裂缝角时,由于走向平均采深比实际采深数值小,导致计算所得角值偏小;采深偏移系数越大,采用平均采深计算所得的角值与实际所得角值之间的相对误差越大;在同等条件下,走向边界角相对误差最大,走向破坏角次之,走向裂缝角相对误差最小。
3.2 采深偏移系数对主要影响半径的影响
采深偏移系数对静态参数的影响主要体现在主要影响半径上。主要影响半径主要用于圈定地下开采对地面的影响范围。主要影响半径的求解如下式所示:

式中:r——主要影响半径,m;
β——主要影响角,(°)。
在考虑松散层影响和不考虑松散层影响两种情况下进行分析采深偏移系数对主要影响半径的影响。
(1)在不考虑松散层影响的情况下,将式(2)带入式(12),则得:
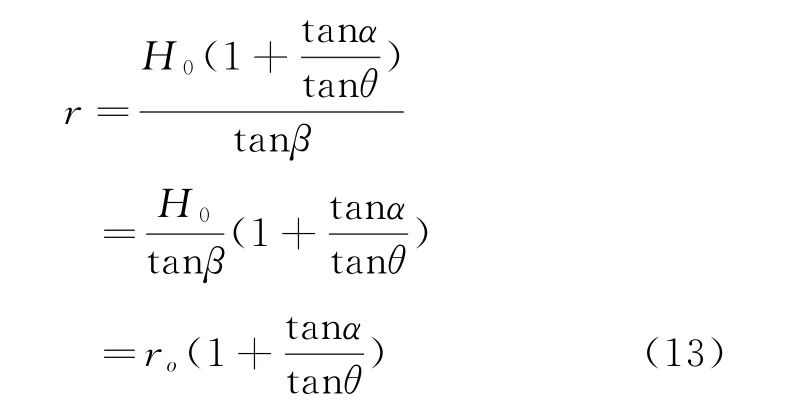
式中:ro——由平均采深计算所得主要影响半径, m。
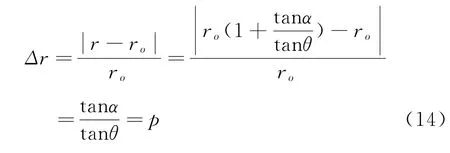
由式(14)可以看出,在不考虑松散层影响的情况下,当平均采深代替走向主断面实际采深时,采深偏移系数和主要影响半径相对误差相等。
(2)在考虑松散层影响的情况下,将式(4)带入式(12),则得:


而主要影响半径的相对误差如下式所示:

由式(16)可以看出,在考虑松散层影响的情况下,用平均采深代替走向主断面实际采深时,采深偏移系数和主要影响半径相对误差相等。
4 结论
在对平均采深引起的采深偏移系数进行几何推导的基础上,得到以下结论:
(1)采动程度对采深偏移系数无影响,松散层对采深偏移系数起稀释作用;
(2)采深偏移系数随着覆岩强度和煤层倾角的增加而不断变大;
(3)在走向主断面上,采深偏移系数越大,采用平均采深计算所得的角值与实际所得角值之间的相对误差越大,且在同等条件下,走向边界角相对误差最大,走向破坏角次之,走向裂缝角相对误差最小。另外,采深偏移系数和主要影响半径相对误差大小一致。
[1] 国家煤炭工业局.建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程[M].北京:煤炭工业出版社,2000
[2] 宋世杰,赵晓光,王双明等.覆岩岩土比对开采沉陷的影响分析与数值模拟[J].中国煤炭,2015 (6)
[3] 邹友峰,邓喀中,马伟民.矿山开采沉陷工程[M].徐州:中国矿业大学出版社,2003
[4] 何国清,杨伦,凌赓娣等.矿山开采沉陷学[M].徐州:中国矿业大学出版社,1991
[5] 李春意,崔希民,何荣等.开采沉陷预计中三维空间曲面拟合参数的研究[J].采矿与安全工程学报,2011(3)
[6] 李春意,陈洁.覆岩移动静态预计模型的构建及实测研究[J].中国煤炭,2012(5)
[7] 曹树刚,刘玉成,刘延保等.基于观测资料的沉陷盆地主断面曲线拟合[J].重庆大学学报,2009 (7)
[8] 陈俊杰,闫伟涛,郭延涛.开采沉陷中采深偏移系数的性质分析[J].河南理工大学学报(自然科学版),2014(6)
[9] 李兴国,文广超.巨厚砾岩层对地表沉降及冲击地压的影响分析[J].中国煤炭,2015(6)
[10] 张广伟,李凤明,李树志等.基于岩体破裂规律的下沉系数变化[J].煤炭学报,2013(6)
[11] 任松,姜德义,杨春和等.岩盐水溶开采沉陷新概率积分三维预测模型研究[J].岩石力学, 2007(1)
Discussion on the related issues of average mining depth in coal mining subsidence
Zhang Xinying,Wang Yuzhen
(Department of Civil Engineering,Henan Vocational College of Water Conservancy and Environment,Zhengzhou,Henan 450008,China)
In the measured data processing of mining subsidence,the average mining depth is often adopted instead of the actual mining depth of the main section along strike.Aiming at the situation,the author solved respectively the mining depth offset coefficients in three different conditions,and classified them again.Then the relationship between the mining depth offset coefficient and the overlying strata lithology or coal seam dip angle was discussed,and the effects of the mining depth offset coefficient on relative parameters were deduced.The results showed that the mining degree had no influence on the coefficient,but the overlying strata strength,the coal seam dip angle had positive correlation with the coefficient.The bigger the coefficient was,the larger the difference value between computational main influence radius and the actual was.
mining depth offset coefficient,unconsolidated formation,main influence radius,relative error
TD173.4
A
张新盈(1977-),男,河南焦作人,讲师,注册测绘师,主要从事矿山测量及测量数据处理方面研究。
(责任编辑 郭东芝)
河南省教育厅重点课题(Z41019)

