朝阳地区降水概率预报模型构建

郭佰汇，吴 丹，范兰艳，冯雪菲，王梦琳

（1.辽宁省朝阳市气象局，辽宁 朝阳 122000；2.辽宁省朝阳市龙城区气象局，辽宁 朝阳 122005；3.辽宁省朝阳县气象局，辽宁 朝阳 122000）

朝阳地区降水概率预报模型构建

郭佰汇1，吴 丹2，范兰艳3，冯雪菲1，王梦琳1

（1.辽宁省朝阳市气象局，辽宁 朝阳 122000；2.辽宁省朝阳市龙城区气象局，辽宁 朝阳 122005；3.辽宁省朝阳县气象局，辽宁 朝阳 122000）

以朝阳地区2005—2013年5—9月降水量记录为基础资料，通过经验法和Spearman、Pearson、Kendall's Tau-b相关系数3种相关性检验法，选出与预报对象相关性好的气象要素作为预报因子。用Logistic回归方法进行有无降水的概率预报，建立了朝阳地区降水概率预报模型。该预报方程具有较高的历史拟合率，为90.7%。将2014年5月1日至10月31日个例作为样本对方程进行检验，当规定降水概率≥40%为有降水时，晴雨预报准确率最高，为86.26%，高于朝阳地区本地晴雨预报准确率3.29百分点，表明该方法对朝阳地区降水具有很好的预报效果。

降水概率预报；Logistic回归；相关系数法

降水是大气系统相互作用的结果，它具有小尺度易变性等特点，在时空分布上具有随机性，因此发布绝对准确的降水预报是不可能的。以往的定性预报用简单的“有”或“无”来描述降水，人为的增大了预报误差。概率预报则以百分率形式对降水出现的可能性大小作出判断，较真实地反映了降水的不确定性，使预报更科学，更客观，更具参考价值。

Logistic回归模型在建立公式时较简单，在理论、数学模型及实用上却都具有很强的生命力。该方法首先是CoxD.R.提出，后经Day N.E.和Korriage D.F.发展，又由Anderson J.A.改进［1-3］。由于大气是一个高度非线性的混合系统，而模式的初始场只是大气真实状态的近似，数值模式所描述的大气过程也是非真实的大气过程，所以单一的确定性预报水平的提高已经变得越来越困难，概率预报成为天气预报发展的必然趋势。Logistic回归模型试用于大量的观测因变量是二分类变量［4］，符合降水发生和不发生的特性，并且它是非线性的，符合大气是非线性的系统的本质。

1 资料与方法

1.1 资料选取

选用朝阳地区国家基准站朝阳县气象观测站（站号54324）2005—2013年5—9月常规地面气象观测站观测历史数据文件（A文件）实况气象资料作为建立预报方程的基础资料，选用2014年5—10月朝阳县站的A文件资料作为预报方程检验的资料，选用朝阳市2014年5—10月晴雨预报资料作为方程检验结果的对比资料。

1.2 方法

1.2.1 相关系数 Pearson相关系数用来判定两个数据集合是否在一条线上面，它用来衡量定距变量间的线性关系。当两个变量都是正态连续变量，而且两者之间呈线性关系时，表现这两个变量之间的相关程度用Pearson相关系数。

Spearman相关系数利用两变量的秩次大小作线性相关分析，对原始变量的分布不作要求，属于非参数统计方法，适用范围要广些。对于服从Pearson相关系数的数据亦可计算Spearman相关系数，但统计效能要低一些。

Kendall's Tau-b相关系数用于反映分类变量相关性的指标，适用于两个分类变量均为有序分类的情况。

1.2.3 因子筛选 因子的选择是影响预报模型准确性的一个重要因素。先对因子进行粗选，以将日常进行降水预报的经验为依据，选择降水预报时会考虑到的各气象要素，包括降水、气压、10 min风向风速、相对湿度、总云量、低云量作为入选因子;这些入选物理量的平均值、最大值、最小值、变化值都作为建立预报模型的一个因子，其中考虑引入24 h变压（P24）、平均气压（Pagv）、最高气压（Pmax）、最低气压（Pmin）、平均相对湿度（Uagv）、最大相对湿度（Umax）、最小相对湿度（Umin）、平均总云量（Zagv）、最大总云量（Zmax）、最小总云量（Zmin）、平均低云量（Dagv）、最大低云量（Dmax）、最小低云量（Dmin）、10 min平均风速（FV10agv）、2时次10 min风向（F2）、8时次10 min风向（F8）、14时次10 min风向（F14）、20时次10 min风向（F20），将这些要素作为待选的预报因子，降水量（R）作为预报对象。

完成因子粗选后进行因子的精选，通过计算粗选因子与预报对象R之间的线性相关系数，挑选相关系数的绝对值较大的各物理量为入选因子，入选因子要通过信度为0.05的相关检验，才能作为精选因子，最后建立预报模型。

在进行相关性检验时，选用Spearman相关，Pearson相关和Kendall's Tau-b相关3种相关性检验方法对粗选因子进行筛选，根据以上3种相关性检验方法，计算得降水量R与各要素之间的相关性如表1。

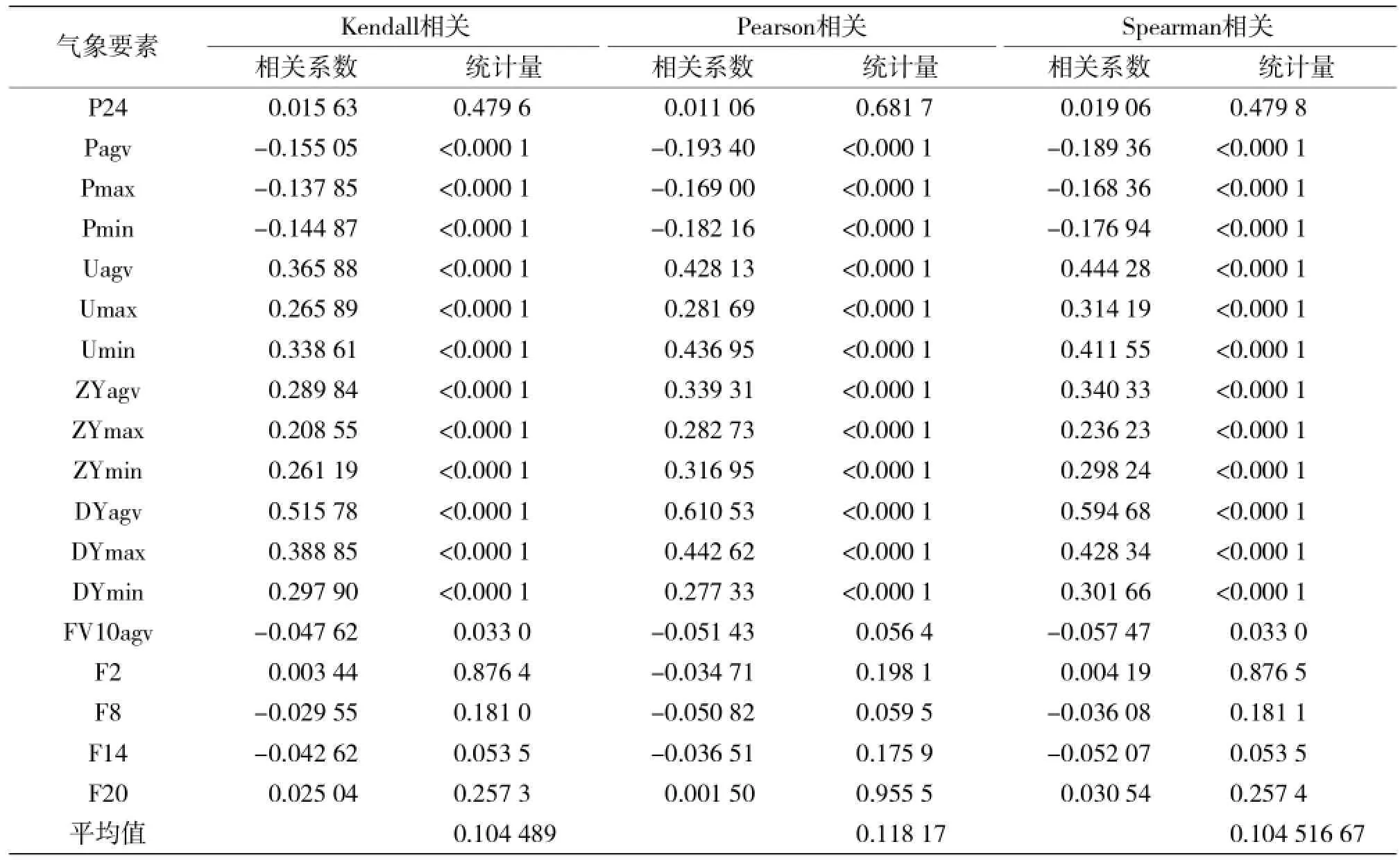
表1 R与各要素间相关性检验

对各检验方法得出的检验统计量进行分析，Pearson相关的检验统计量的平均值明显大于Spearman相关和Kendall's Tau-b相关，Spearman相关和Kendall's Tau-b相关的检验统计量的平均值基本相同，表明这两种相关性检验中各要素对R的总体相关性更优。以 Spearman相关和Kendall's Tau-b相关检验的结果作为因子精选的参考，发现这2种检验方法筛选出的因子是相同的，最终选取了13个物理量（Pagv、Pmax、Pmin、Uagv、Umax、Umin、Zagv、Zmax、Zmin、Dagv、Dmax、Dmin、FV10agv）作为建立预报模型的因子。

2 结果与分析

利用2005—2013年5—9月共1 377 d的历史个例样本，由所筛选出的13个气象要素因子，通过Logistic回归方法建立朝阳地区降水概率预报方程如下。

经检验，该预报方程具有较高的历史拟合率，为90.7%，采用似然比检验、SCORE检验、Wald检验，Pr＞ChiSq且都小于0.000 1，说明预报因子对预报对象的影响是显著的，所建立的降水概率预报方程是有意义的。将2014年5月1日至10 月31日8：00～8：00时时段共182 d的个例作为样本进行试报，182 d的天气个例中，48 d出现降水（其中5 d为微量降水），134 d无降水。分别以10%～50%作为划分是否预报出现降水的概率，对降水预报结果如表2。

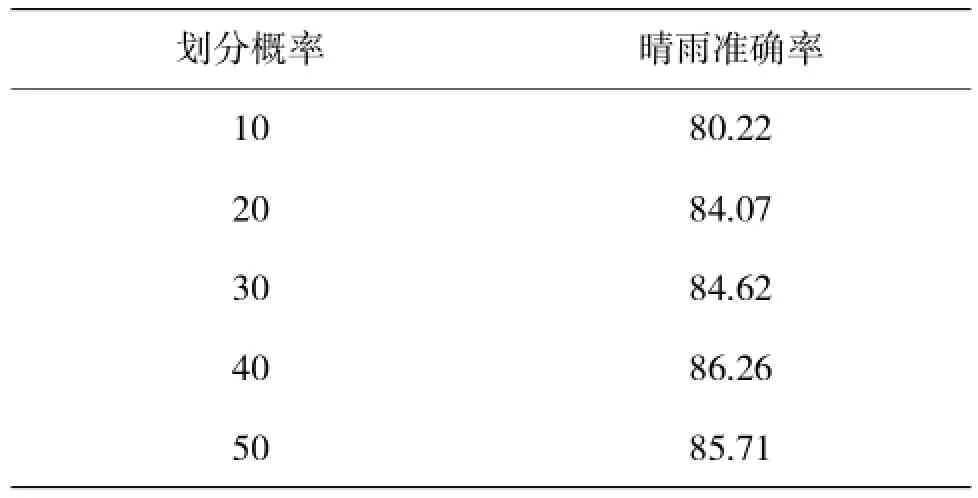
表2 晴雨预报准确率 %

从结果可以看出，当划分概率为40%时，晴雨预报准确最高，为86.26%。对比朝阳市本地预报结果，在2014年5—10月期间朝阳地区8：00～8：00时时段的晴雨预报准确率为82.97%，这比本文预报方法的准确率低了3.29百分点，可见用logistic回归模型建立的降水预报模型对于朝阳地区的预报效果是非常好的。

3 小结与讨论

将降水作为预报对象，以A文件中部分资料作为预报因子，并用经验法和相关性检验法对预报因子进行粗选和精选，通过logistic回归方法，建立了朝阳地区降水概率预报模型。利用2005—2013年5—9月资料建立的方程具有较高的历史拟合率，为90.7%。将2014年5月1日至10月31日个例作为样本对方程进行检验，当规定降水概率大于等于40%为有降水时，晴雨预报准确率最高，为86.26%，高于朝阳地区本地晴雨预报3.29百分点，表明该方法对朝阳地区降水具有很好的预报效果。当然，该预报方法还有一定的不足，在建立方程以及检验方程时，只应用了降雨资料，未考虑降雪以及秋冬季、冬春季交替时常出现的雨夹雪等情况，这些需要在以后的研究中不断补充。

［1］ COX D R.Some procedure associated with the logistic qualitative response cure［C］//Neyman Ed，F N David Research Rapers in Statistics：Festschrift for J.New York：Wiley，1966.

［2］ BOCCHIERI J R.Use of the logicmodel to transform predictors for precipitation type forecasting［C］//Amer：Preprint 6th Conf.on Probability and Statistics in Atmos Sci Amer：Meteor Soc，1979.

［3］ 纪玲玲，王昌雨，张志华.Logistic回归及其在概率降水预报中的应用［J］.解放军理工大学学报，2003，4 （5）：92-94.

［4］ 汪海波，罗莉，吴 为，等.SAS统计分析与应用［M］.北京：人民邮电出版社，2013.

［5］ 吕纯濂，陈杰伦.Logistic及其在气象上的应用［J］.南京气象学院学报，1982，5（1）：112-123.

［6］ 万夫敬，袁慧玲，宋金杰，等.南京地区降水预报研究.南京大学学报，2012，48（4）：513-525.

［7］ 汤 浩.新疆降水概率预报技术研究.新疆气象，2003，26（1）：5-7.

［8］ 黄永新.南宁市降水概率预报方法研究.广西气象，1997，18（1）：49-52.

（本文责编：陈 珩）

P456.8

A

1001-1463（2015）07-0031-03

10.3969/j.issn.1001-1463.2015.07.011

2015-04-23

辽宁省朝阳市项目《基于logistic模型的降水概率预报》

郭佰汇（1989—），女，辽宁朝阳人，助理工程师，主要从事天气预报预警研究工作。联系电话：（0）13591876815。E-mail：guobaihui@sina.com