木质纤维素酶水解分形动力学的研究进展

柳 咪 迟聪聪，2，* 龚亚辉 李鸿魁 吴养育（.陕西科技大学轻工与能源学院，陕西省造纸技术与特种纸品开发重点实验室，陕西西安，7002；2.齐鲁工业大学，制浆造纸科学与技术教育部重点实验室，山东济南，2505；.中兴通讯股份有限公司，陕西西安，70065）

·木质纤维素分形动力学·

木质纤维素酶水解分形动力学的研究进展

柳 咪1迟聪聪1，2，*龚亚辉3李鸿魁1吴养育1
（1.陕西科技大学轻工与能源学院，陕西省造纸技术与特种纸品开发重点实验室，陕西西安，710021；
2.齐鲁工业大学，制浆造纸科学与技术教育部重点实验室，山东济南，250353；
3.中兴通讯股份有限公司，陕西西安，710065）

木质纤维素作为地球上储量最丰富的可再生资源之一，可用于生产燃料乙醇，以减少人类对石化资源的依赖。酶水解作为重要步骤之一，自然引起了国内外的广泛关注。但由于酶水解是一个复杂的异质多相反应过程，很难用一个简单的模型对其进行表征。分形理论作为一种研究方法，直接从非线性复杂系统入手去认识其内在规律，更为客观、真实地反映了事物的内在本质。本文阐述了木质纤维素酶水解分形动力学的研究现状，并在此基础上对其应用前景进行展望。

木质纤维素；酶水解动力学；分形

近年来，资源短缺与能源危机日益加剧，人们越来越关注于寻找一种可持续利用的生物质能源，以减少人类对传统化石资源的依赖和增加绿色能源使用［1-3］。木质纤维素是地球上储量最丰富的一种生物质资源，其转化燃料乙醇是一个复杂过程，主要包括预处理、酶水解、发酵以及分离纯化等步骤。其中，酶水解是一个动态反应过程，为探究其行为机理需要进行动力学研究，这通常要对酶水解过程的步骤进行假设，在此基础上推导酶水解动力学模型，最后利用该模型研究影响酶水解效率的因素及规律。近年来，越来越多的方法或理论应用于木质纤维素酶水解的研究，分形理论就是其中之一，它从复杂的非线性系统入手，从抽象和未简化的研究对象本身去认识其内在规律，更为客观、真实地反映事物的内在本质［4］。酶水解动力学与分形理论相结合，即酶水解分形动力学，利用分形维数与反应速率常数可以描述不同条件下的酶水解反应历程，简化了研究过程。本文就分形理论应用于木质纤维素酶水解动力学的研究现状进行综述，并对其前景进行展望。

1 分形理论概述

分形概念源于Mandelbrot［5］对海岸线测量问题的研究。对于海岸线这类不规则图形，若选取的测量尺度不同，测量结果也会有差异。也就是说，现实中这种复杂的不规则图形，并没有准确的周长。随着测量尺度的减小，它的周长将逐渐向无穷大趋近。如果这种不规则情况呈现出大尺度与小尺度测量相似的特征，并且无限细分下去都存在着自相似性，那么就称这种几何形状为分形。一般认为分形应具有精细的结构、自相似性、标度不变性、可迭代产生、无限不规则等性质，其中标度不变性和自相似性是分形最基本的特征［6］。

分形的特点可以用分形维数（又称分数维或分维）来描述。维数是空间理论和几何学的基本概念，它源于经典的欧几里德空间。在欧几里德空间中，确定几何图形或物体中任一点位置所需的独立坐标就称为该几何图形或物体的维数，即欧氏维数。欧氏维数总是整数，如点的维数是0，直线的维数是1，平面的维数是2，立方体的维数则是3，但欧氏维数的缺陷在于不能描述不同几何图形的不规则程度，所以需要引入分形。在分形空间里，图形的分形维数可以不是整数值［7］，分形维数越大则越复杂，反之就越简单。通常笼统地把取非整数值的维数称为分形维数，用字母D来表示，即：

式中，N（r）为利用新单位度量1个原有单位所度量图形的个数，1/r为原单位长与新单位长的比值［8］。D为整数时，分形维数与欧式几何的空间维数意义相同。

近20年来，分形理论已得到广泛的应用，在物理、化学、生物学、天文学、材料学、计算机图形学、经济学、哲学等相对独立的领域呈现了大量研究成果。事实上，不同学科领域的现象之间存在惊人的相似性，因此分形理论可能成为联结现代各学科的纬线［9-12］。

2 木质纤维素酶水解

2.1木质纤维素化学组成

木质纤维素主要由纤维素、半纤维素和木素三大组分构成。纤维素分子有序地排列成束状微纤丝，构成了细胞壁的骨架，半纤维素和木素基质充满骨架之间。纤维素分子排列可形成结晶区和非结晶区（无定形区），前者对纤维素酶水解具有抵抗作用，后者则易于发生酶水解反应［13］。半纤维素是无定形聚合物，其链上连接着相当数量的乙酰基导致结构产生分支，比较容易水解，水解产物是单糖及少量糖酸，其存在会阻碍纤维素酶与纤维素直接接触，可加入半纤维素酶除去半纤维素以提高水解效率。木素是苯丙烷结构单元通过碳碳键和醚键连接而成的一种结构复杂的芳香族高聚体，难以被微生物降解，其化学性质比较稳定，是木质纤维素生产燃料乙醇的主要障 碍［14-16］。

2.2酶水解机理

纤维素酶是指能催化纤维素发生水解作用的一系列复合酶，根据催化反应功能可以分为外切葡聚糖酶、内切葡聚糖酶和β-葡萄糖苷酶3大类，这3种酶协同完成木质纤维素的水解作用。

目前，纤维素酶分解木质纤维素的理论假说大致有3种［17-18］：协同理论、初反应假说理论和碎片理论。其中协同理论最为普遍，该理论认为，由于木质纤维素的特异性，其分解需要不同酶如内切葡聚糖酶、外切葡聚糖酶和β-葡萄糖苷酶等的协同作用，三者比例合理时就能协同完成对纤维素的水解作用。即内切葡聚糖酶首先内切无定形纤维素产生新的末端，外切葡聚糖酶从末端外切纤维素链，产生纤维二糖或葡萄糖，纤维二糖会对内切葡聚糖酶和外切葡聚糖酶产生抑制作用，β-葡萄糖苷酶的参与可消除这种抑制作用［19］。

2.3酶水解的影响因素

为寻求最适宜的水解条件，提高糖化效率，有必要对纤维素酶水解进行深入研究。影响木质纤维素酶水解的因素主要有底物、酶水解条件及纤维素酶［20］。就底物本身来说，相对较小的颗粒尺寸、较大的比表面积及表面孔径，均有利于提高酶水解效率。底物浓度过高会对酶水解产生抑制作用，降低酶水解速率，但底物浓度太低会导致所得葡萄糖浓度较低，从而影响其工业应用价值［21］。酶水解条件主要包括温度、缓冲液pH值及酶用量等。多数研究显示，纤维素酶作用底物的最佳温度范围为45～65℃，最适宜的pH值范围为4.0～5.5［22-23］。酶的活性越高越有利于提高水解效率，纤维素酶水解效率随酶用量的增加先增大而后趋于稳定，说明在一定条件下，一定量的纤维素分子能与纤维素酶的结合位点数有限，当这些结合位点全部被纤维素酶分子占据时，再增加酶用量已对水解不起作用，反而会浪费酶，对提高经济效益产生不利影响［24］。木质纤维素酶水解液中主要存在3种糖：纤维二糖、葡萄糖及木糖，随着酶解时间的延长，这3种糖的浓度逐渐增加，进而抑制纤维素酶的活性。

3 酶水解分形动力学

3.1酶水解动力学

一般认为，木质纤维素酶水解是一个两相反应过程：固相反应是内、外切葡聚糖酶在木质纤维素底物表面吸附，进而将其分解成纤维二糖的反应过程；而β-葡萄糖苷酶将纤维二糖分解成葡萄糖的过程则是液相反应。整个酶水解反应是一个串联反应过程，上一反应的产物是下一反应的底物，整个反应过程环环相扣，其中一个因素发生变化就会影响整个反应过程，因而酶水解动力学的描述相当困难，不能简单用一个动力学方程来进行表征。

木质纤维素酶水解动力学模型都是在一定的假设和简化下得到的，简化的合理性与否，对所得模型会产生很大影响。一般将木质纤维素酶水解简化为以下两个步骤：

图1 木质纤维素酶水解简化模型

近年来，有人在上述简化模型的基础上，建立有效的酶水解动力学模型。庄新姝等人［25］以桉木为原料，经170～200°C高温液态水预处理后进行酶水解，研究得出以下酶水解动力学模型如式（2）所示。

式中，ki为反应速率常数；Eαi为反应活化能，kJ/mol；R为气体常数；T为反应温度；ki0为常数。利用线性拟合，对该模型中的反应速率常数ki和活化能Eαi求解，最后求解酶水解糖得率。通过对比检验，该动力学模型可以较准确地描述桉木的酶水解历程，但推导过程较繁琐，并且在得知该模型参数（ki、Eαi）后对糖得率的求解过程也比较复杂。刘姗姗［26］以湿氧化预处理后的杨木作为反应底物，酶水解后用DNS法测定水解液中的还原糖浓度，经过一系列推导得出酶水解动力学方程如式（3）所示。

式中，YC为纤维转化率，％；K为常数；C为酶用量，FPU/g；α为 C的指数；k2为反应速率常数；

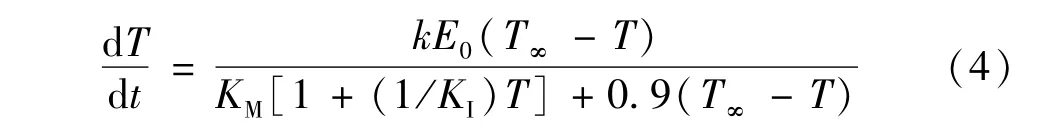
式中，T为还原糖浓度，t为糖化时间，k为速率常数，E0=0.45，T∞为预处理后稻草生成的最大还原糖浓度，KM为米氏常数，KI为产物抑制常数，0.9为葡萄糖换算成淀粉的换算系数。对酶水解数据（主要是相关常数）进行拟合，发现超声波辅助预处理可明显提高速率常数k，米氏常数KM降低，即提高了底物与酶的亲和力，抑制常数K1则变化细微，上述现象说明超声波辅助预处理比单纯的化学预处理更有利于促进稻草的酶水解。

综上所述，由于木质纤维素酶水解过程是异相反应，且反应速率常数不断降低，准稳态理论不成立，再加上木质纤维素底物的结构复杂，酶水解反应动力学较复杂，不能采用传统的米氏方程进行描述［29］。而分形的研究对象是复杂、抽象和未简化的非线性系统，不仅可以认识其内在规律、反映事物的内在本质，还可以简化研究过程，由此便产生了酶水解分形动力学。然而，由酶水解动力学数据模拟得出的h值大多不符合Kopelman［30］的研究结果。t为时间。对木质纤维素酶水解数据进行拟合得到相应参数值如下：K=17.84，α=0.4244，k2=0.2023，模型拟合度仅为0.8658，精确度不够高，有必要进一步优化。段媛等人［27］以脱木素的桉木木粉为反应底物，研究得出纤维素及半纤维素的水解方程，通过matlab拟合求得其反应速率常数，经比较发现己糖和木糖的生成速率均小于分解速率，表明超临界水解不利于单糖的累积，对于5-羧甲基糠醛而言，其生成速率大于分解速率，说明超临界条件有利于5-羧甲基糠醛的累积。鲁爱华等人［28］以酸、碱及其辅助超声波预处理后稻草为反应底物，对其酶水解过程经过一系列简化和假设后得到产物还原糖生成速率的动力学方程如式（4）所示。

式中，h是分形维数，ds是描述分形结构中动力学行为的重要参数。一些研究者得出的h有时大于1，无法由此得出ds，因此他们认为酶水解动力学过程符合类分形动力学规律。

3.2分形动力学模型的建立

近年来，研究人员就酶水解分形动力学进行了相关研究，提出不同的分形动力学模型，部分模型经充分简化后，基本可以对酶水解过程的变化规律进行描述。

20世纪80年代，Kopelman［31］提出了一种新型的分形动力学方法，可以实现对异质反应的动力学过程进行描述。该方法认为，一般均质溶液动力学的基础是小分子物质在三维空间中的分子扩散运动，而在二维空间中，小分子物质的扩散速率要慢得多，这将导致反应速率具有时间迟滞性。分形动力学认为该条件下反应的速率常数具有时间衰变特征，即

其中，k为速率常数，h为分形维数，t是时间，而kt是t的速率系数，1表示一个时间单位。当0＜t ＜1时，速率系数与普通动力学反应相同；当t≥1时，速率系数与时间和分形维数有关。木质纤维素酶水解过程中，反应时间远大于一个时间单位，故其速率常数与时间和分形维数有关。现有文献中的酶水解分形动力学模型大都在此基础上推导。

目前，分形动力学已被用于分析高聚集态大分子的复杂反应［32］。Priit Valjamae等人［33］对木质纤维素酶水解的数据进行拟合，提出以下一级分形反应动力学模型见（7），该模型主要描述酶水解过程中纤维二糖随时间的变化规律。

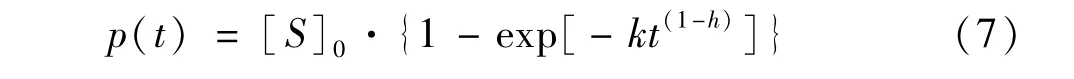
式中，p（t）表示反应生成纤维二糖的浓度，μmol/L；［S］0为木质纤维素的起始浓度，μmol/L；t为反应时间；k和h为经验常数。

Xu等人［34］将分形维数引入Michaelis-Menten动力学方程来分析木质纤维素酶水解过程，通过分维的变化来分析引发这一变化的本质原因，而不是对这一变化过程的具体机理进行解释。Wang等人［35］在一级反应动力学的基础上推导出下述动力学方程见式（8）：

式中，X表示葡萄糖转化率；C是残余还原糖浓度；C0是底物中总还原糖浓度；k是速率常数；h是分形维数。

张宇等人［36］对甘蔗渣的酶水解类分形动力学进行研究，将复合纤维素酶对底物中葡聚糖的作用当作单一酶的作用，并假定速率与时间呈幂函数关系，同时将酶水解反应看作一级反应，最后推导出还原糖浓度与时间的关系方程见式（9）。

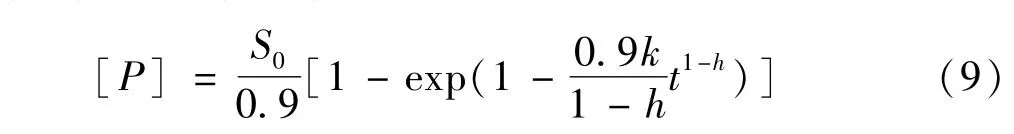
式中，［P］为葡萄糖浓度，g/L；S0为底物中葡聚糖浓度，g/L；k为速率常数；h为分形维数。

3.3分形动力学模型的应用

现有文献资料显示，分形动力学模型采用2个参数k和h可以成功描述不同条件预处理后木质纤维素的酶水解过程，其中采用分形动力学方程对每种酶水解实验数据进行一元回归拟合，如此便会拟合出不同条件下的速率常数k和分形维数h。速率常数与普通反应中的初始速率对应，它除了与底物的表面特性、反应活性等有关，还与纤维素酶用量及其活性有关。分形维数描述的是纤维素酶水解过程中反应速率的时间迟滞现象，是反应的内在特征参数，一般情况下它的变化范围是0～1［31］，随底物添加量及纤维素酶用量的变化而有规律地变化。反应条件也会对分形动力学参数产生影响，如高温条件下纤维素酶的失活、各种抑制剂（如葡萄糖、纤维二糖、预处理木质纤维原料时释放的木质素、酚类物质等［37］）的影响。因此，该动力学方程可实现对木质纤维素酶水解的整个过程进行全面描述。

Priit Valjamae等人［33］研究酶水解过程中外切纤维素酶与内切葡聚糖酶的协同作用发现，酶水解底物浓度越低，分形维数h越小，越有利于底物的水解作用。这是由于底物浓度较低时，酶就会较多地吸附在其表面，由此酶的平均扩散距离就会变短，弥补了较低的横向扩散速率，进而有利于底物的有效降解。

Wang等人［38］对微晶纤维素的酶水解进行研究，发现随着时间的延长，水解速率减缓。底物与酶的协同作用对速率常数与分形维数有明显影响，随着酶与纤维素比值的增加，速率常数先上升而后趋于平稳，这可能与纤维素酶对纤维素的吸附能力有关。速率常数越大，说明纤维素酶的吸附能力越强。当酶与纤维素的比值进一步增大而速率常数不再增加时，吸附达到饱和状态，过量的纤维素酶并未参与酶水解，会造成纤维素酶的浪费。分形维数随酶与纤维素比值的增加呈上升趋势，一方面是因为比值越大，纤维素酶会聚集在纤维素表面，而不会在表面进行扩散；另一方面是由于纤维素酶的二维结构，当酶浓度较高时，会在溶液内部聚集进而阻碍纤维素酶在纤维素表面的扩散。木素对速率常数与分维影响的研究结果表明，木素的存在会导致分形维数增加，进而抑制木质纤维素的水解作用。要解决这一问题，可以通过添加非离子表面活性剂等来消除木素的抑制作用，从而增加速率常数，减小分形维数，提高水解效率。

Wang等人［35］还在不同条件下对木质纤维素的酶水解作用进行分形动力学分析，结果表明，当速率常数一定时，木质纤维素的水解效率随分形维数的增加而降低；当分形维数保持不变时，速率常数越大则水解效率越高。当分形维数保持相对较高值时，木质纤维素的水解效率会在短时间内达到最大值，并且保持不变。

张宇等人［36，39］采用不同方法对甘蔗渣进行预处理，然后用分形的方法对酶水解数据进行一元回归拟合，将拟合得到的速率常数k和分形维数h与底物颗粒的不规则性及木素含量进行比较分析，结果表明分形维数只与底物有关，与酶和反应条件无关，预处理残渣的形状越不规则，木素含量越高，分形维数越大。

分形理论在木质纤维素酶水解过程中的应用，不仅可以对复杂过程进行简化描述，更重要的是，可为非线性理论用于木质纤维素的研究开辟一条新途径，还可为人们研究木质纤维素的化学组成、特性及功能结构提供有益的启示。

4 结语与展望

木质纤维素转化为燃料乙醇是一项具有挑战性的课题，而作为其中重要一环的酶水解也备受关注。为阐明酶水解相关机理，许多学者就酶水解动力学展开了相当量的研究工作，并建立动力学模型进行表征，但都存在一定弊端。分形理论作为一种研究方法，可以实现对结构或过程的非线性描述，近几年已被应用到酶水解动力学的研究中，但相关报道较少。随着分形理论与分析检测技术的发展与完善，酶水解分形动力学的研究具有较大的发展潜力，相信在不久的将来会出现新的创造性成果。

［1］ Pal Borjesson.Good or bad bioethanol from a greenhouse gas perspective-What determines this？［J］.Applied Energy，2009，86（5）：589.

［2］ Hammond G P，Kallu S，ManusM C.Developmentofbiofuels for the UK automotivemarket［J］.Applied Energy，2008，85（6）：506.

［3］ ZHAO Xiao-ling.Biorefiniery technology and bioenergy innovation ［J］.China Pulp＆amp；Paper，2012，31（12）：51.赵晓玲.生物质精练技术和生物质能源创新［J］.中国造纸，2012，31（12）：51.

［4］ Mandelbrot B B，Passoja D E，Paullay A J.Fractal character of fracture surfaces ofmetals［J］.Nature，1984，308：721.

［5］ Mandelbrot B B.How long is the coastof britain？Statistical Self-Similarity and Fractional Dimension［J］.Science，1967，156：636.

［6］ Kenneth Falconer.Fractal geometry：mathematical foundation and applications［M］.Chichester：John Wiley＆amp；Sons Ltd，1990.

［7］ LIHouqiang，CHEN Guangyue.Fractal and fractal dimensions［M］.Chengdu：Sichuan Education Press，1990.李后强，程光钺.分形与分维［M］.成都：四川教育出版社，1990.

［8］ Wu Dacheng，Du Zhongliang，Gao Xushan.Nanofiber［M］.Beijign：Chemical Industry Press，2003.吴大诚，杜仲良，高绪珊.纳米纤维［M］.北京：化学工业出版社，2003.

［9］ Li Yongguo，Yan Zhongcheng.Fractal theory and its applications in biological sciences［J］.Journal of Capital Normal University（Natural Science Edition），2009，30（1）：43.李永国，颜忠诚.分形理论及其在生命科学中的应用［J］.首都师范大学学报，2009，30（1）：43.

［10］ Zhuang Qiang，Li Tiehu，Qingxiang Chen，et al.Fractal theory and applications in activated carbons［J］.Carbon Techniques，2009，28（6）：36.庄 强，李铁虎，陈青香，等.分形理论及其在活性炭研究中的应用［J］.炭素技术，2009，28（6）：36.

［11］ Yin Youfa.Fractal theory and its applications in the research of carbon materials（Ⅰ）-Fractal theory and themeasurement of fractal dimension［J］.Carbon Techniques，1992（2）：1.印友法.分形理论及其在炭素材料研究中的应用（1）—分形理论及分形维数的测定［J］.炭素技术，1992（2）：1.

［12］ Huang Rui.The research ofwood cell image edge detection based on the fractal theory［D］.Haerbin：Northeast Forestry University，2012.黄 睿.基于分形理论的木材细胞图像边缘检测研究［D］.哈尔滨：东北林业大学，2012.

［13］ L T Fan，Y Lee，Beardmore D H.Mechanism of the enzymatic hydrolysis of cellulose：Effects ofmajor structural features of cellulose on enzymatic hydrolysis［J］.Biotechnology and Bioengineering，1980，22（1）：177.

［14］ Bauer W D，Talmadge K W，Keegstra K，et al.The structure of plant cellwalls：II.The hemicellulose of thewalls of suspension-cultured sycamore cells［J］.Plant Physiology，1973，51（1）：174.

［15］ Chandra R P，Bura R，MabeeW E，et al.Substrate pretreatment：The key to effective enzymatic hydrolysis of lignocellulosics［J］.Biofuels，2007，108：67.

［16］ Ikeda T，Holtman K，Kadla JF，et al.Studies on the effect of ball milling on lignin structure using amodified DFRCmethod［J］.Journal of Agricultural and Food Chemistry，2002，50（1）：129.

［17］ Yu Weiqi.The study of pretreatmentand enzymatic hydrolysisof eucalyptus raw materials［D］.Guangdong：South China University of Technology，2012.尉慰奇.桉木原料的预处理及其酶解糖化的研究［D］.广州：华南理工大学，2012.

［18］ Gupta R，Lee Y Y.Mechanism of cellulase reaction on pure cellulosic substrate［J］.Biotechnology and Bioengineering，2009，102（6）：1570.

［19］ Michihhiro Fujii，Jun-ichi Mori，Taira Homma，et al.Synergy be-tween an endoglucanase and cellobiohydrolases from Trichoderma koningii［J］.The Chemical Engineering Journal and the Biochemical Engineering Journal，1995，59（3）：315.

［20］ Xia An.The kinetics ofand influencing factors in enzymatic hydrolysis of cellulose［D］.Chengdu，Sichuan University，2002.夏 安.纤维素酶水解动力学及影响因素研究［D］.成都：四川大学，2002.

［21］ Lisa Rosgaard，Pavle Andric，Kim Dam-Johansen，et al.Effects of substrate loading on enzymatic hydrolysis and viscosity of pretreated barley straw［J］.Applied Biochemistry and Biotechnology，2007，143（1）：27.

［22］ Zhou Jian，Luo Xuegang，Su Lin.Research progress and prospect on the enzymatic hydrolysis for cellulose［J］.Science and Technology in Chemical Industry，2006，14（2）：51.周 建，罗学刚，苏 林.纤维素酶法水解的研究现状及展望［J］.化工科技，2006，14（2）：51.

［23］ Luo Guimin.Enzyme engineering［M］.Beijing：Chemical Industry Press，2003.罗贵民.酶工程［M］.北京：化学工业出版社，2003.

［24］ Huang Yi.The hydrolysis mechanics of cellulose and influencing factor［J］.Shandong Chemical Industry，2007，36（5）：31.黄 翊.纤维素酶水解机理及影响因素［J］.山东化工，2007，36（5）：31.

［25］ Zhuang Xinshu，QiWei，Yuan Zhenhong，et al.Study on kinetics of eucalyptus sawdust pretreated by liquid hotwater［J］.Acta Energiae Solaris Sinica，2011，32（10）：1487.庄新姝，亓 伟，袁振宏，等.高温液态水预处理桉木水解动力学的研究［J］.太阳能学报，2011，32（10）：1487.

［26］ Liu Shanshan.Optimization ofpoplarwood residues pretreatmentand kinetics of different hydrolysismeasures［D］.Beijing：Chinese A-cademy of Forestry Sciences，2012.刘姗姗.杨木废弃物预处理技术和水解反应动力学的研究［D］.北京：中国林业科学研究院，2012.

［27］ Duan Yuan，Wan Jinquan，Wang Yan，etal.Study on saccharification of eucalyptus lignocelluloses hydrolysis and reaction kinetics in supercriticalwater［J］.Acta Energiae Solaris Sinica，2013，34（4）：689.段 媛，万金泉，王 艳，等.桉木纤维超临界水解糖化及其反应动力学的研究［J］.太阳能学报，2013，34（4）：689.

［28］ Lu Aihua，Yuan Xingzhong，Kang Guangbo，etal.Kinetic study on enzymatic hydrolysis of rice straw with ultrasound-assisted pretreatment［J］.Chinese Journal of Environmental Engineering，2010，4（6）：1399.鲁爱华，袁兴中，康广博，等.稻草经超声波辅助预处理后酶解过程的动力学研究［J］.环境工程学报，2010，4（6）：1399.

［29］ Prabuddha Bansal，Melanie Hall，Matthew JRealff，etal.Modeling cellulase kinetics on lignocellulosic substrates［J］.Biotechnology Advances，2009，27（6）：833.

［30］ Xin Houwen.Reaction dynamics of fractal media［M］.Shanghai：Shanghai Science＆amp；Technology Education Press，1997.辛厚文.分形介质反应动力学［M］.上海：上海科技教育出版社，1997.

［31］ Raoul Kopelman.Fractal reaction kinetics［J］.Science，1988，241（4873）：1620.

［32］ Schnell S，Turner T E.Reaction kinetics in intracellular environments with macromolecular crowding：simulations and rate laws［J］.Progress in Biophysics and Molecular Biology，2004，85（2、3）：235.

［33］ Priit Valjamae，Kalle Kipper，Goran Pettersson，et al.Synergistic cellulose hydrolysis can be described in terms of fractal-like kinetics ［J］.Biotechnology and Bioengineering，2003，84（2）：254.

［34］ Feng Xu，Hanshu Ding.A new kinetic model for heterogeneous（or spatially confined）enzymatic catalysis：Contributions from the fractal and jamming（overcrowding）effects［J］.Applied Catalysis A：General，2007，317（1）：70.

［35］ Zhilong Wang，Hao Feng.Fractal kinetic analysis of the enzymatic saccharification of cellulose under different conditions［J］.Bioresource Technology，2010，101：7995.

［36］ Zhang Yu，Xu Jingliang，Yuan Zhenhong，etal.Comparison of different pretreatmentmethods on sugarcane bagasse and fractal-like kinetics of enzymatic hydrolysis［J］.Advances in New and Renewable Energy，2013，1（2）：166.张 宇，许敬亮，袁振宏，等.甘蔗渣的不同预处理方法比较及其酶水解的类分形动力学［J］.新能源进展，2013，1（2）：166.

［37］ Eduardo Ximenes，Kim Youngmi，Nathan Mosier，et al.Inhibition of cellulases by phenols［J］.Enzyme and Microbial Technology，2010，46（3/4）：170.

［38］ ZhilongWang，Jian-He Xu，Hao Feng，et al.Fractal kinetic analysis of polymers/nonionic surfactants to eliminate lignin inhibition in enzymatic saccharification of cellulose［J］.Bioresource Technology，2011，102：2890.

［39］ Yu Zhang，Jingliang Xu，WeiQi，etal.A fractal-like kinetic equation to investigate temperature effect on cellulose hydrolysis by free and immobilized cellulase［J］.Applied Biochemistry and Biotechnology，2012，168（1）：144.CPP

（责任编辑：常 青）

Research Progress in the Fractal K inetics of Lignocellulose Enzymatic Hydrolysis

LIU Mi1CHICong-cong1，2，*GONG Ya-hui3LIHong-kui1WU Yang-yu1
（1.Shaanxi Key Lab of Papermaking Technology＆amp；Specialty Paper，College of Light Industry＆amp；Energy，Shaanxi University of
Science＆amp；Technology，Xi'an，Shaaxi Province，710021；2.Key Lab of Pulp and
Paper Science＆amp；Technology of Ministry of Education，Qilu University of Technology，Ji'nan，Shandong Province，250353；
3.Zhongxing Telecommunication Equipment Corporation，Xi'an，Shaaxi Province，710065）
（*E-mail：congcongchi@163.com）

Lignocellulose is a promising alternative energy source for the limited fossil oil，which can be used for fuel ethanol bioconversion.As an importantstep，enzymatic hydrolysis has attracted greatattention all over theworld.However，it's difficult to be characterized by using a simplemodel，since enzymatic hydrolysis process is a complex heterogeneous reaction.As an effective research method，fractal theory directly illustrates the inherent law from complicated nonlinear system，reflecting the intrinsic essencemore objectively and truly.The paper mainly rewiewed the research progress of fractal kinetics of enzymatic hydrolysis.And the prospects of its potential applications were also presented.

lignocellulose；kinetics of enzymatic hydrolysis；fractal

柳 咪女士，在读硕士研究生；研究方向：木质纤维素转化为燃料乙醇。

TQ353

A

0254-508X（2015）08-0062-06

2015-03-30（修改稿）

陕西省自然科学基础研究计划青年人才项目（2015JQ3077）；制浆造纸科学与技术教育部重点实验室开放基金（KF201401）；教育部高等学校博士学科点专项科研基金（20126125120002）；陕西科技大学校内科研基金（BJ11-18＆amp；2012SB028）。

*通信作者：迟聪聪女士，E-mail：congcongchi@163.com。