一种扫频干扰信号参数估计方法

周利华 ， 常 琪 ，2

（1.中国电子科技集团公司 第三十六研究所，浙江 嘉兴 314033；2.通信信息控制和安全技术重点实验室 浙江 嘉兴 314033）

对雷达干扰信号的分析是现代高科技战争中电子设备抗干扰和战场电磁频谱监视分析的重要前提和有力保障，通过对电磁信号环境的认知，雷达还可以更加合理有效的发挥自身对电磁频谱的使用和控制能力，在保证目标探测性能的基础上，有效的规避干扰和反辐射攻击。因此，雷达干扰信号分析技术有着重要的军事意义和研究前景[1-2]。

周期波形调频干扰信号可以在有效的干扰带宽内获得均匀且带宽较宽的干扰频谱，因此在实际电子战中有着较为广泛的应用[3]。本文主要讨论的是对基于时频分析的锯齿波扫频干扰信号的分析和参数估计。

1 锯齿扫频干扰信号简介

设f（t）是以Tm为周期的锯齿波形，周期锯齿调频干扰信号复数表示式为[4]

式中，Uj为干扰信号振幅，在每个周期间隔内 （mT0＜t＜

周期锯齿波调频干扰的频率调制波形如图1所示，Tm为调制周期，fm=1/Tm为调频斜率，ΔF为频偏值。

图1 周期锯齿波频率调制波形Fig.1 Periodic sawtooth wave frequency modulation waveform

图2 是对扫频干扰信号经过接收机检测接收前后的信号时域波形和频谱的仿真图。

设扫频干扰信号的扫频带宽为5 MHz，接收机带宽为2 MHz。由以上仿真结果我们可以看到，5 MHz的扫频干扰信号的扫频带宽大于接收机接收带宽时，干扰信号能量不能进入接收机，所以经接收机检测后其时域波形由连续波变为周期间断出现的波形，周期为调制信号周期。接收机检测到信号出现的时间长度由扫频宽度接收机带宽以及调制信号周期共同决定。

2 时频分析技术

图2 过接收机前后的锯齿扫频干扰（左图为没过接收机，右图为过接收机后）Fig.2 Sweep frequency interference before and after receiver

在常用的时频分析方法中，Cohen类的平滑伪Wigner-Ville分布能兼顾时间分辨率和频率分辨率的问题，在需要同时获得较高的时间分辨率和频率分辨率时具有广泛的应用。为了更好的介绍平滑伪Wigner-Ville分布，先介绍Wigner-Ville分布。

Wigner-Ville分布（简称WVD）是一种二次型的时频能量分布算法，对信号s（t）的WVD定义为[5-6]

或用 s（t）的频谱 S（ω）表示

WVD是信号的双线性函数，在使用中会产生相干项，这些产生的相干项会与信号项产生重叠，从而使得对WVD的图像很难做出直观的解释。因而不用于对于非平稳信号的时频分析。

通过对时域和频域添加窗函数长度是可以独立控制的窗函数，最后得如下分布

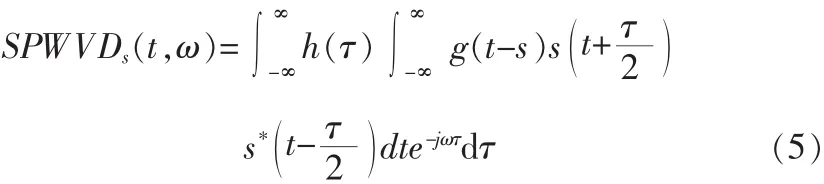
这种分布称为平滑伪Wigner-Ville分布（简称SPWVD）。式中，h（t）和 g（t）为两个相互独立的窗函数。这种独立平滑处理的结果可以有效的抑制WVD中出现的交叉项干扰，此外，此算法的时域分辨率和频域分辨率可以通过对两个相互独立的平滑窗长度的控制根据实际需要进行调节，因此能同时在时域和频域上获得较高的分辨率。

锯齿扫频干扰信号在无系统噪声和在干噪比为3 dB的系统噪声环境下的WVD分布和SPWVD分布的时频关系等高线如图3和图4所示。

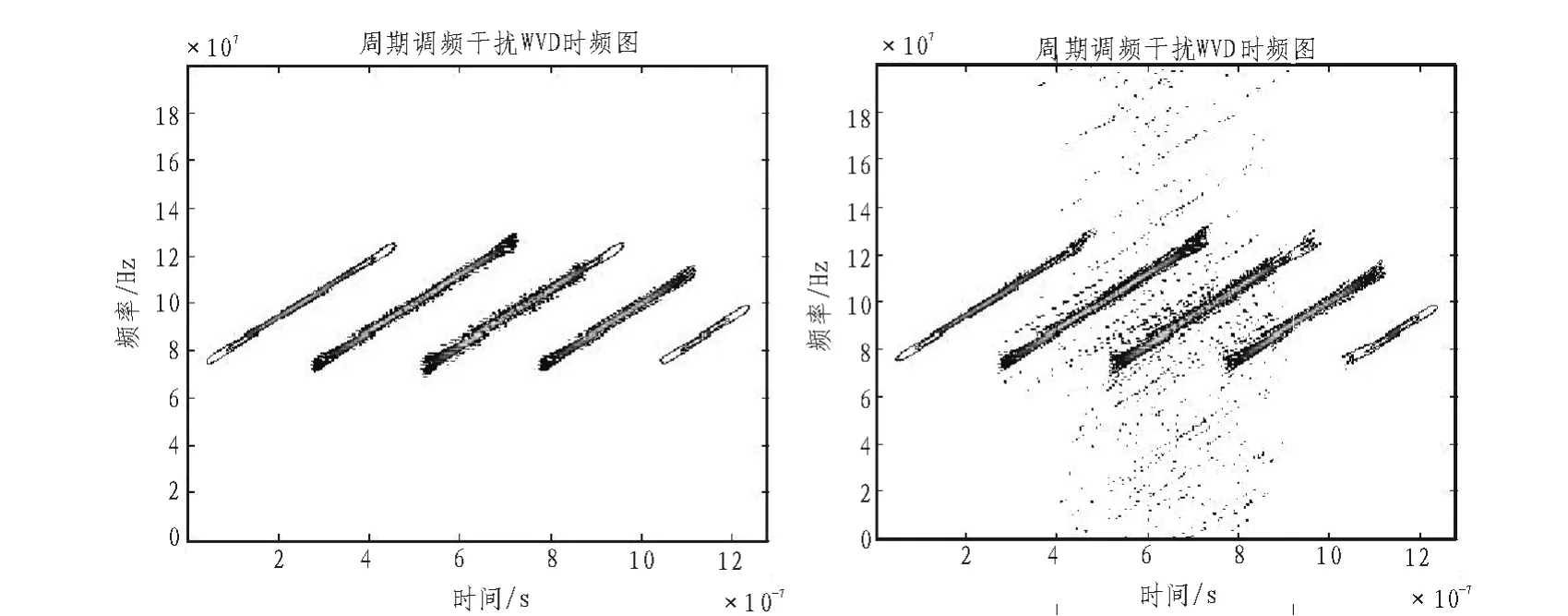
图3 不同干信比条件下WVD等高线（左图为无噪声，右图JNR=3dB）Fig.3 Contour map of WVD under different JNR

从上图中各时频分析仿真结果的对比中我们可以看出，SPWVD分布具有良好的抑制交叉干扰项的效果，时频分析的结果也具有良好的时频集聚性；且在3dB噪声环境条件下，SPWVD分布几乎看不到噪声的影响，说明SPWVD还具有良好的噪声抑制能力。因此SPWVD可以作为有系统噪声信号的条件下有效的时频分析方法。

3 锯齿扫频干扰信号的时频分析方法

图4 不同干信比条件下SPWVD等高线（左图为无噪声，右图JNR=3dB）Fig.4 Contour map of SPWVD under different JNR

已知雷达接收机带宽为2 MHz，干扰数据为采用正交I路和Q路两路采样接收到的基频信号，正交采样频率为2 MHz。图5画出了雷达接收机在连续十个脉冲重复周期里接收到的目标回波信号和锯齿扫频干扰信号的时域幅度图，图5的十幅图中每幅图的横轴为采样点数，纵轴为接收到的干扰信号的幅度值。图6中图形说明与图5相同。

根据能量检测法和恒虚警的检测原理，设置合适的接收机检测门限，采用硬截断的方式，使小于门限信号的幅度值为0，经过检测后的信号幅度图如图9所示。

根据第2节中接收机检测对扫频干扰信号影响的分析结果，从图6中可以看出，干扰信号具有明显的周期性，忽略由雷达接收机相应特性及近地杂波的影响，已知雷达接收机采样频率为2 MHz的情况下，对多个周期的干扰信号进行统计平均

通过计算可得其扫频周期为T=10 ms。

又已知雷达接收机的带宽为2M，根据每个周期内干扰信号的存在时间长度，可求得扫频信号的扫频带宽。通过对多个周期的干扰信号求得的扫频带宽进行统计平均可得到

通过计算可得扫频干扰信号的扫频带宽为ΔF=5 M。

取其中一个周期干扰信号内的一部分进行细微特征分析，图7画出了截取一个周期内的经过门限检测后部分干扰信号的时域波形和信号包络（上图为时域波形，下图为信号包络）。

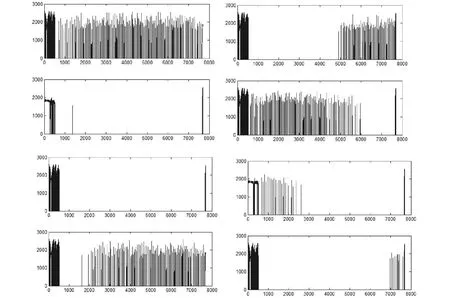
图6 过检测门限后的目标回波和干扰信号的幅度图Fig.6 The amplitude of target echo and jamming signal after detection threshold

图7 部分干扰信号的时域波形和信号包络Fig.7 Time-domain waveform and signal envelope of part jamming signal

从图7中我们可以看出，每个周期内的干扰信号仍然具有明显的周期性。

上图8画出了扫频干扰信号的SPWVD分析的仿真结果。从图8经过统计计算可得，小周期T1≌19μs，信号时宽Ta≌1.9μs，因已知雷达的接收机带宽为2 M，可以求得周期扫频的扫频带宽为20 M，综合以上分析求得的扫频干扰个特征参数可得，雷达接收机接收的扫频干扰信号的频率调制信号为一个大周期的锯齿波和小周期的锯齿波经过叠加后的复合锯齿波调制信号，可以得到雷达扫频干扰信号频率调制模型如图9所示。

4 结束语

文中通过对实际接收干扰信号的分析处理结果，有效的验证了SPWVD较好的时频分析效果。它能有效的解决传统时频分析中时间分辨率和频率分辨率不能兼顾的问题，在信号处理中有着广阔的应用前景。

[1]赵国庆.雷达对抗原理[M].西安:西安电子科技大学出版社，2012.

[2]范伟.雷达有源干扰信号特征分析与识别算法研究[D].成都:电子科技大学，2007.

图8 SPWVD变换的平面图和三维图Fig.8 Contour map and three-dimensional figure of SPWVD

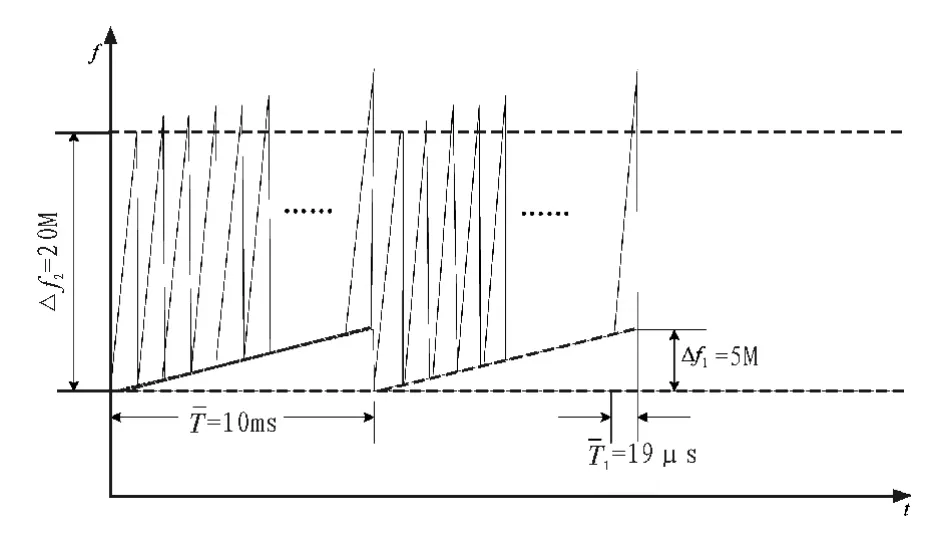
图9 扫频干扰信号频率调制模型Fig.9 Sweep Jamming signal frequency modulation model

[3]易咸煜.雷达有源干扰识别及抗干扰措施优化选取[D].成都:电子科技大学，2010.

[4]赵惠昌，张淑宁.电子对抗理论与方法[M].北京：国防工业出版社，2010.

[5]胡昌华，周涛，夏启兵，等.基于Matlab的系统分析与设计—时频分析[M].西安：西安电子科技大学出版社，2002.

[6]范树凯.非线性调频信号的时频分析及其应用[D].无锡:江南大学，2008.