基于支持向量机的配电线路高阻接地故障检测方法

郑星炯

（广东电网公司 佛山顺德供电局，广东 佛山 528300）

近年来，中性点小电阻接地方式在我国一些城市配电网和工矿企业配电网中得到应用。在这些配电网中，当配电线路掉落在树枝、干燥地面、潮湿沙地上时，会引起高阻接地故障[1-2]。高阻接地故障大部分是单相的，过渡电阻阻值大（一般大于100Ω）且显非线性特征，故障点往往伴随有间歇性电弧的产生。高阻接地故障发生后，流过故障线路的电流值远小于传统电流保护的电流整定值，继电保护装置不动作。但配电网在高阻故障下长期运行会引发火灾、触电等事故，需要及时检测出高阻故障并加以排除。

近年来，配电网高阻故障检测逐渐引起人们的关注。文献[2]利用高阻故障发生时故障线路的电压和电流基频及谐波变化规律识别高阻故障，但在开关操作、负荷投切、电容器投切时容易发生误判。文献[3]建立了配电线路高阻故障模型，分析了故障线路和健全线路在不同频带内的小波系数特征，并提取特征频带能量特征，以此提出了一种配电网高阻故障的检测方法。文献[4]利用故障线路电流3次谐波分量与故障相电压在故障发生时相位相同的原理检测高阻故障，但受谐波分量低及检测装置灵敏度的影响。文献[5]分析了中性点有效接地配网高阻故障的零序电流特征，提出了基于零序电流波形凹凸性分析的检测方法，但不能应用于小电流接地系统。

本文提出了一种基于支持向量机的配电线路高阻接地故障检测方法。首先，建立高阻接地故障检测的支持向量机；其次，对线路的零序电流进行傅里叶分解，获得零序电流信号的基波分量、整数次谐波分量及非整数次谐波分量，并以此构成3维特征向量；最后，以3维特征向量作为输入，通过支持向量机判断线路是否发生高阻接地故障。

1 配电线路高阻接地故障特征分析

配电网发生单相高阻接地故障时，过渡电阻呈非线性，故障点往往伴随有电弧，导致故障电流存在严重的畸变。

图1描述了小电阻接地系统中单相高阻接地故障发生前后故障线路上三相电流的变化情况。高阻故障发生时，故障点经大电阻接地，通过对故障线路的零序电流进行频谱分析，发现零序电流仍然以工频分量为主，含有一定量的整数次谐波（以奇数次谐波为主），此外还含有一定量的频率为工频非整数倍的间谐波；若故障是金属性接地故障，线路零序电流中的间谐波相对含量较高阻故障要低。而对健全线路的三相电流进行频谱分析时，发现三相电流中谐波及间谐波含量远低于故障线路，且零序电流很小。

图1 故障线路三相电流波形Fig.1 Current waveform of high impedance faulty feeder

配电网的上述故障特征为高阻接地故障的检测提供了一定的依据。但进一步研究表明，在小电阻接地系统中发生金属性接地与高阻接地故障时，零序电流的基波、谐波和间谐波含量之间很难找到能区分两种故障的分界明确的阈值，从而也很难提出直接的高阻接地故障检测判据。为此，本文借助支持向量机的机器学习能力和模式识别、分类能力实现高阻接地故障检测。

2 故障特征向量的获取

设置采样频率fs=50N（N为1个工频周期内的采样点数，本文取N=64），对零序电流信号进行采样，取故障后发生后10个周期的采样数据 i（n）（其中 n=1，2，…，10N）进行离散傅里叶变换：

式中，I（m）为频率f=5 mHz的零序电流的有效值，m=0，1，2，…，5N-1。

参照IEC标准IEC 61000-4-7:1991[6]及其谐波子群和间谐波子群的概念（谐波和间谐波计算示意图如图2），同时考虑频率分辨率，定义k次谐波的有效值为：

显然，I1即为基波的有效值。设置特征量x2为基波电流能量，即 x1=I21。

设置特征量为各整数次谐波电流的能量和，即：

式中，H为谐波的最高次数，本文中取H=31。

除直流分量、基波和整数次谐波外，其它频率分量为间谐波。设置所有间谐波的能量为特征量，即：

由特征量x1、x2、x3构造3维特征向量，作为下述支持向量机的输入向量 x=[x1，x2，x3]。

3 基于支持向量机的高阻故障检测

3.1 线性可分支持向量机算法

支持向量机是根据结构风险最小化原则提出的一种新型模式识别方法。无论是在小样本，还是非线性、高维度的模式识别问题中，支持向量机都具有优于神经网络等其他智能技术的特质。为识别配电线路是否发生高阻故障，本文引入线性可分支持向量机[7]。

给定训练集 T={（x1，y1）， …，（xL，yL）}， 其中 xiI^x=Rn，yi={1，-1}，i=1，…，L，若存在 w I^Rn，b I^R，使得对所有使 yi=1 的下标 i，有（w·xi）+b≥1；而对所有使 yi=-1 的下标 i，有（w·xi）+b≤-1，则称训练集T线性可分。其最大间隔法的线性支持向量机的算法如下：

1）给定训练集 T={（x1，y1），…，（xL，yL）}

2）构造并求解下式二次规划问题，解出x，b

3）构造分类超平面（w·xi）+b=0，由此得到决策函数 y=sgn（w·xi+b）

为求解上述二次规划问题中的w，b，引入拉格朗日函数：

则上述最优化问题转化为：

3.2 样本选择及支持向量机训练

设配电线路发生高阻故障时支持向量机输出yi=1，正常运行或发生其它故障时输出yi=－1。

通过仿真，获得小电阻接地配电网在各种运行方式和负荷水平条件下正常运行、发生金属性接地故障及发生高阻接地故障时线路的零序电流波形，通过对零序电流波形的采样和傅里叶变换，获得的特征向量[x1，x2，x3]，构成支持向量机的学习样本，按照4.1节支持向量机算法，通过反复训练使支持向量机建立起特征向量与是否发生高阻故障的映射关系，最终获得式（10）形式的决策函数。

3.3 高阻故障检测实现步骤

利用支持向量机检测配电线路高阻接地故障的实现步骤如下：

1）采用继电保护启动算法，当发现配电线路出现扰动后，对该线路零序电流采样10个周波（0.2秒）；

2）对采样数据进行傅里叶变换，并按照公式（1）～（6）计算特征向量，并将该特征向量作为已训练好的支持向量机的输入；

3）若支持向量机输出为1，表示线路发生高阻故障；若支持向量机输出为－1，表示线路未发生高阻故障。

4 仿真研究

4.1 配电网故障仿真模型

采用MATLAB仿真软件，利用SIMULINK中的Sim Power System模块，建立如图3所示中性点经小电阻接地配电网的仿真模型，获取正常运行及在线路L1发生单相高阻接地故障时的线路L1～L5上的零序电流信号。

图 3 中 10 kV 配电网中，馈线 L1、L2、L3、L4、L5 的长度分别为 5 km、6 km、8 km、10 km 和 7 km。线路参数：正序电阻：r1=0.014Ω/km，零序电阻 r0=0.39Ω/km；正序电感 l1=0.9 mH/km，零序电感l0=4.2 mH/km；正序电容c1=11.8μF/km，零序电容c0=7.5μF/km。

配电线路发生高阻故障时，故障点伴有不规则电弧，接地电阻表现出强烈的非线性特征。高阻故障模型对仿真结果是否可信十分重要。目前描述电弧的经典模型有Cassie模型、Mayr模型等[8]。本文选用适合10 kV配电网的Mayr模型，并将电弧模型串联电阻Rg来模拟高阻故障。

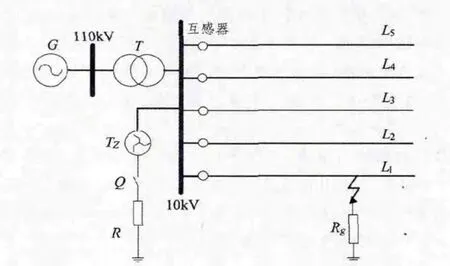
图3 配电网仿真模型Fig.3 Distribution network simulation model

4.2 样本选择及仿真结果

本文通过仿真获得配电网在不同负荷水平 （负荷在10～90%范围内以10%递增变化）、不同故障合闸角度（角度在0～350°间以 10°递增变化）、不同接地电阻（0～80 Ω 范围内以10Ω递增变化，在100～3 200Ω范围内倍增变化，接地电阻默认高于150Ω为高阻故障）及多种扰动（电容器投切，负荷突然增减）情况下的线路零序电流样本，共300个；其中100个样本用于作为支持向量机的训练样本，余下的200个样本作为支持向量机的验证样本。

将训练样本用于支持向量机训练，再采用训练好的支持向量机对验证样本进行分类，识别高阻故障和非高阻故障，识别正确率为93.5%。对识别错误的样本进行统计，发现当单相接地电阻为接近150Ω（高阻故障设置阈值）时，有误判现象；当单相接地电阻大于1 200Ω时，高阻故障也不能有效检测；此外，当故障合闸角接近0或大于340°时，也有高阻故障误判为非高阻故障的情况。对于后两者情况，分析认为是故障时由于接地电阻太大，或故障发生时刻接近于电压过零点，导致故障特征量过小，高阻故障不能有效检测，本文方法还有进一步改善的空间。在其它情况下，高阻故障的检测效果是令人满意的。

5 结 论

配电网高阻接地故障检测是长期困扰配电网保护运行的一项难题，本文在此进行了有益的尝试，并取得了较好的效果。

1）本文建立了小电阻接地配电网单相高阻故障仿真模型，分析了配电线路发生单相高阻接地故障时零序电流的频谱分布特征，并在此基础上提出了一种基于支持向量机的高阻接地故障检测方法。

2）选用由零序电流基波、谐波及间谐波能量构成3维特征向量，作为支持向量机输入，使得样本线性可分，可运用线性支持向量对样本进行分类，大大降低了支持向量设计难度及训练计算量。

3）仿真研究表明，本文提出的小电阻接地系统高阻接地故障检测方法具有较高的检测准确度，对负荷水平和扰动不敏感；但在接地电阻过大或在电压过零点发生故障时，由于故障特征量过小，检测精度有所下降，本文方法有进一步改进的空间。

[1]徐丙垠，李天友，薛永端．智能配电网建设中的继电保护问题[J]．供用电，2012，29（4）:17-25.XU Bing-yin，LI Tian-you，XUE Yong-duan.Relay protection issues in construction of smart distribution system[J].Distribution&Utilization，2012，29（4）:17-25.

[2]Yong Sheng，Rovnyak SM.Decision tree-based methodology for high impedance fault detection[J].IEEE Transactions on Power Delivery，2004，19（2）:533-536.

[3]陈民铀，黄永，瞿进乾．配电网线路高阻故障识别方法[J]．重庆大学学报，2013，36（9）:83-88．CHEN Min-you，HUANG Yong，ZHAI Jin-qian.High impedance fault identification method of distribution network[J].Journal of Chongqing University，2013，36（9）:83-88.

[4]Lien K Y，Chen SL，Liao CJ，et al．Energy variance criterion and threshold tuning scheme for high impedance fault detection[J]．IEEE Transactions on Power Delivery，1999，14（3）:810-817．

[5]耿建昭，王宾，董新洲，等．中性点有效接地配电网高阻接地故障特征分析及检测[J]．电力系统自动化，2013，37（16）:85-91.GENG Jianzhao，WANG Bin，DONG Xinzhou，et al.Analysis and detection of high impedance grounding fault in neutral point effectively grounding distribution network[J].Automation of Electric Power Systems，2013，37（16）:85-91.

[6]IEC 61000-4-7:1991，Electromagnetic Compatibility（EMC）-Part 4-7:Testing and measurement techniques-General guide on harmonics and inter-harmonics measurements and instrumentation，for power supply systems and equipment connected thereto[S].IEC，1991.

[7]邓乃杨，田英杰.支持向量机：理论、算法与拓展[M].北京：科学出版社，2009.

[8]Elkalashy N，Lehtonen M，Darwish H，et al.Modeling and experimental verification of a high impedance arcing fault in MV networks[J].IEEE Transactions on Dielectrics and Electrical Insulation，2007，14（2）:375-383.