基于约束粒子群优化的克里金插值算法

贾 雨，邓世武，姚兴苗，蔡元菲

（1.成都理工大学 核技术与自动化工程学院，成都610059；2.电子科技大学 通信与信息工程学院，成都611731）

克里金（Kriging）插值［1］是基于地质统计学变差函数模型发展起来的空间插值方法，是利用区域化变量的原始数据和变差函数的结构特点，对未采样点的区域化变量的值进行最优、线性、无偏估计的一种方法，广泛应用于地下水模拟、油气储层建模预测、煤层分布估计等领域。自1951年由南非采矿工程师D.G.Krige提出至今，克里金方法的发展已形成了一套完整的理论体系，并产生了一些实际有效的程序和软件。

为了有效地提高插值精度，许多学者对克里金插值算法进行了改进。严华雯［2］等通过利用加权最小二乘法优化遗传算法中的适度函数，改进普通基于遗传算法优化的克里金插值方法；邵才瑞［3］等针对克里金具有平滑性，神经网络难以反映变量的空间相关性等缺点，用变差函数修正神经网络的目标函数，并利用遗传算法对神经网络进行全局优化形成了一种遗传神经克里金混合插值方法。克里金插值的系数是以变差函数的计算为基础的，早期变差函数的拟合方法主要依赖于专业人员的地质经验和对地质数据特征的了解，直接给出理论变差函数的参数，没有客观的标准。在实际应用过程中，为提高变差函数的拟合精度，学者们提出了多种变差函数的拟合方法：加权最小二乘法、极大似然法、遗传算法等等。

变差函数拟合是一个最优化问题，加权最小二乘法和极大似然法常常陷入局部最优而无法得到全局最优解，同时解的稳定性问题也是长期困扰我们的难点问题。遗传算法有较好的全局寻优能力，且对目标函数是否可导没有限制；但是该方法需要调整的参数较多，结构复杂，影响算法的执行效率。为此，本文通过改变粒子群算法中粒子多样性，结合地质变量的特征和数据特征，提出了一种改进的插值方法——基于约束粒子群优化的克里金插值算法，通过改进变差函数的拟合精度，提高克里金插值的精度。

1 克里金插值的基本原理

克里金插值是建立在变差函数空间分析的基础上，对有限区域内的区域化变量取值进行无偏最优化估计的一种方法。假设区域化变量为Z（x），待插值点为x0，样本点记为xi（i＝1，2，…，n），在点xi处的属性值记为Z（xi），则待插值点x0处的属性值是各个样本点属性值的加权和，记为

其中：λi为采样点xi的权重系数。相距为h的2个空间点x、x＋h处的函数值Z（x）和Z（x＋h）之间的方差称为变差函数，其数学表达式为［4］

γ＊（h）为实验变差函数，h为滞后距［5］。对于不同的滞后距h，计算出不同的实验变差函数值γ＊（h）后需用一个合理的理论变差函数模型对其进行拟合［6，7］。常用的模型有线形模型、球状模型、指数模型和高斯模型［8］等。以高斯模型为例，基本公式如下

其中：C0为块金常数；C0＋C为基台值；C为拱高。当时，γ（h）近似达到最大值C0＋C，所以高斯模型的变程约为当C0＝0，C＝1时，称为标准高斯模型。在区域化变量满足二阶平稳的条件下，可推导出克里金方程组

其中：γ（xi，xj）是观测点xi与xj之间的变差函数值；γ（xi，x0）是采样点xi与内插点x0之间的变差函数值；μ是与方差最小化有关的拉格朗日乘数。由此方程计算出权重λi的值，代入公式（1）中即可求出待估点x0处的内插值Z（x0）。

2 基于约束粒子群优化的克里金算法

2.1 粒子群算法原理

粒子群算法（PSO）是根据适应度函数使得粒子达到最优位置的一种优化算法。群体中的每个粒子都有其自身的位置和速度，且粒子的位置和速度是变化的。粒子移动的速度与两个因素有关：粒子到目前为止的最好位置和群体中所有粒子到目前为止的最好位置。

假设粒子在Q维空间中移动，群体中粒子的个数为N0，则第i个粒子的位置表示为：Xi＝（xi1，xi2，…，xi0），根据适应度函数，可以得到每个粒子的历史最优位置和群体中所有粒子的最优位置，第i个粒子的历史最优位置pbest为：Pi＝（pi1，pi2，…，pi0），群体最优位置gbest表示为Pg，是所有Pi（i＝1，2，…，N0）中的最优，表达式为：Pg＝（pg1，pg2，…，pg0）。第i个粒子的移动速度为：Vi＝（vi1，vi2，…，vi0）。

在每次迭代时，粒子根据以下公式更新自己的速度和位置

其中：k为当前迭代数；ω为惯性权重因子，表示粒子维持原来速度的程度；c1和c2为加速常数，分别代表将粒子推向个体最优位置pbest和群体最优位置gbest的权重；ξ和η是［0，1］区间内均匀分布的随机数；γ为收敛因子。

2.2 基于约束粒子群克里金插值算法

粒子群优化算法直接应用于克里金插值会出现早熟、变差函数的拟合不符合实际地质规律等问题，为此本文采用高斯变异、地质规律约束等方法进行改进，具体方法如下。

2.2.1 高斯变异

大量的研究表明，由于PSO算法按照追随种群最优粒子的策略进行迭代更新，算法易陷入局部最优和早熟收敛等缺陷。鉴于此，本文采用一种基于高斯变异的方法来提高种群的多样性。在算法出现过早收敛时，能够使粒子在解空间中的其他区域进行搜索，跳出局部最优，寻找更优的解。改变粒子多样性的方法如下。

在迭代到一半次数后，开始对粒子进行变异。对每个粒子以概率P进行高斯变异［9］。其中P一般根据函数的复杂性和经验来决定。粒子变异的公式如下

其中：gbestd为全局最优在d维的值；σ为高斯白噪声。

2.2.2 权重系数的设定

一般情况下，用最小二乘法拟合变差函数的时候，适应度函数由公式（8）给定

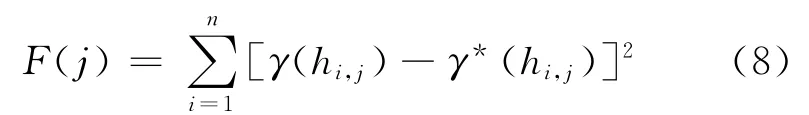
其中：F（j）为第j个粒子的适应度函数值；hi，j为第j个粒子的第i个滞后距；γ（hi，j）为第j个粒子在第i个滞后距处的变差函数值；γ＊（hi，j）表示第j个粒子在第i个滞后距处的实验变差函数值。

通过对适应度函数增加权重系数来描述对某些实验变差函数值的加重，以强化地质因素和拟合要求。根据研究，权重系数λi的选择与以下3个因素有关。

a.滞后距：实验变差函数中滞后距较小的几个点比较大地反映了区域化变量的变异程度，在变差函数拟合时，需要着重考虑滞后距较小的头几个实验变差函数值，使该处的误差尽量小，即适应度函数值尽量小。

b.样本点的密度：在实际的地质问题中，样本点在平面上的分布是极不均匀的。例如在石油勘探的应用中，通常钻井或测井数据是我们的样本数据，而井位在平面上的分布极不均匀，有的区域井很多，有的区域井很少。在克里金插值过程中，样本点少的区域，其样本点的权重相对较大；样本点多的区域，其样本点的权重相对较小。

c.样本点的绝对值：样本点的绝对值可能相差很大，直接使用公式（8）构建适应度函数，可能出现绝对值大的样本点对适应度函数贡献过大，绝对值小的样本点对适应度函数贡献过小的问题。

根据上述问题，给出新的适应度函数

其中

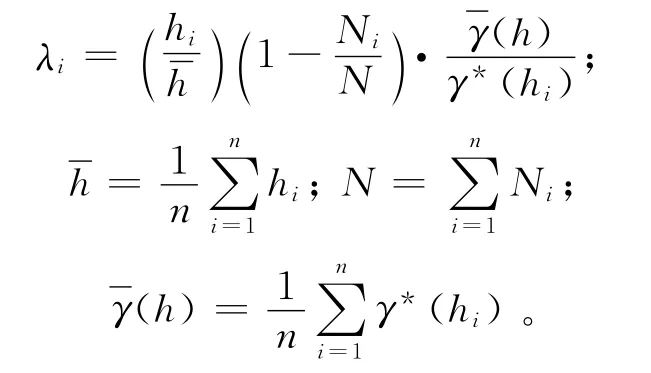
λi表示每个样本点的权重系数；hi为滞后距；Ni为对应滞后距处的样本对数；为实验变差函数值的平均值。

2.2.3 参数搜索范围的约束

由于理论变差函数模型的每个参数都具有实际的物理含义，对每个参数给出搜索范围，以符合实际规律。给定待拟合参数的搜索范围，每进行一次迭代后，判断参数是否在设定的搜索范围内。若参数已经超过限定的搜索范围，则采取如下方式进行处理

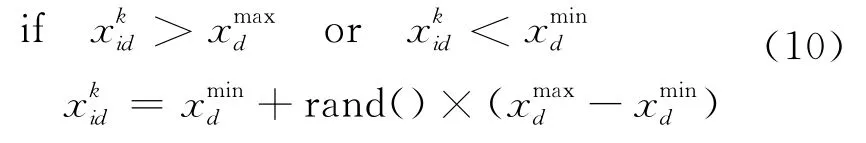
3 基于约束粒子群优化的克里金插值算法的实现

本文选择高斯模型，根据粒子群算法，将理论变差函数中的未知参数（a，C，C0）看作一个粒子，每个粒子包含a、C和C0这3个分量，基于约束的粒子群优化算法步骤如下。

第一步，初始化：设定粒子个数m，生成一个粒子群X＝｛x1，x2，…，xm｝，根据待拟合参数的物理意义，设定参数的取值范围：0＜a＜两点之间距离的最大值，0＜C＜实验变差函数值的最大值，C0≥0；在各参数的取值范围内，随机取m个值，作为每个粒子的初始位置，并将其设置为当前个体最优位置pi。设置粒子各个分量的最大速度值（d表示粒子的第d个分量），在中随机取值，作为粒子第d个分量的初速度；设置最大迭代次数n。

第二步，根据滞后距hi及对应滞后距处的样本对数Ni，计算权重系数λi。

第三步，根据适应度函数计算各个粒子的适应度函数值F（j）。

第四步，根据下面2个公式，确定粒子i的当前最优位置以及整个粒子群当前的全局最优位置

其中：表示第i个粒子经过k次迭代后的当前最优位置表示经过k次迭代后的全局最优位置。

第五步，根据下面的粒子速度和位置更新公式，更新粒子的位置

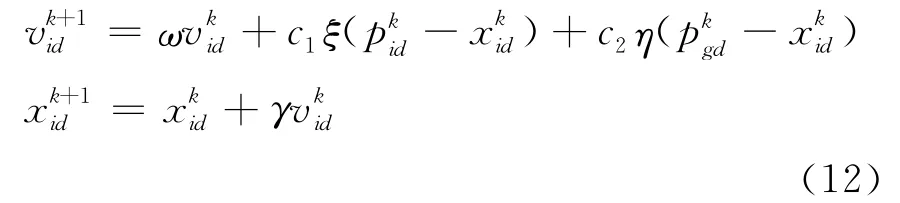
第六步，判断粒子当前速度和位置是否超过设定的范围，如果是，则在搜索范围内为该粒子重新随机取值。

第七步，迭代次数达到最大迭代次数的一半后，对每个粒子按50%的概率进行高斯变异，防止其陷入局部最优。

第八步，返回第三步，重复该计算过程，直到满足终止条件（达到最大迭代次数或预定的最小适应度函数值），此时获得了一个理想的最优解。

4 实际数据测试结果分析

本文所用的数据是采样得到的实测数据，该数据包含坐标、深度、速度、层位名称等。对于拟合算法的仿真只是针对二维情况下的插值，从这些数据中，只需要提取出某个层位的实测数据坐标、深度值和速度值。

4.1 拟合效果比较

分别利用最小二乘法、基于约束的PSO算法对实验变差函数进行拟合得到的参数，如表1所示。

实验变差函数的散点以及拟合后的理论变差函数曲线如图1所示。图1中，蓝色代表计算出来的实验变差函数散点；红色曲线为最小二乘法拟合出的理论变差函数曲线；绿色曲线代表利用约束的PSO算法得到的理论变差函数曲线。由图可知，本文提出的约束粒子群优化算法在滞后距较小的地方取得的了较好的效果；而在滞后距较大的地方，变差函数值更接近于基台值C0＋C。结合表1中的数据也可得知：相较于最小二乘法，本文提出的方法具有较小的基台值，更接近实验变差函数值的稳定值（由后几个实验变差函数值反映出来）。

4.2 插值效果比较及误差分析

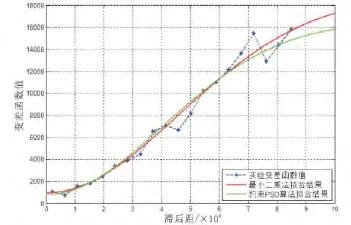
图1 最小二乘、约束PSO拟合变差函数对比曲线图Fig.1 Contrast figure of the variation functions fitted by the least squares method and the constraint PSO

表1 拟合后的理论变差函数模型参数值Table 1 Parameters of the theoretical variation functions after fitting

利用上文中得到的理论变差函数模型对待插值点进行属性值估计。本文对1 000×1 000个待插值点进行属性值估计。待插值点的坐标表示为

其中：xmin表示已知点x坐标的最小值；ymin表示已知点y坐标的最小值；xstep代表x方向的步长；ystep代表y方向的步长；i，j分别是从0到999的整数。运用本文4.1节中获得的2种理论变差函数曲线对待插值点做插值处理得到的插值效果如图2所示。从图中可看出，采用约束的PSO算法拟合后变差函数插值结果高点更清晰。实际钻井和地质分析也证实了本文方法的有效性。

为进一步比较两种拟合算法得到变差函数的精度，本文采用交叉验证的方法。对已知点进行插值处理，将计算得到的属性值与真实的属性值之差作为误差，如图3所示。对已知的94个样本点插值后，在大部分已知点处，利用本文提出的基于约束粒子群优化的克里金插值算法得到的误差更小。图中最后一条数据为平均误差，从中也可以看出本文提出的方法优越于常规克里金插值算法。

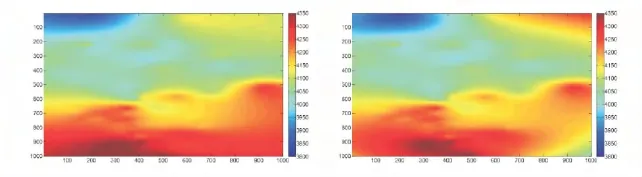
图2 使用最小二乘法拟合变差函数的插值（左图）和使用约束的PSO算法拟合的插值结果Fig.2 Interpolation renderings with variation functions fitted by the least squares method and the constraint PSO

图3 最小二乘法和约束的PSO变差函数插值后误差分析Fig.3 Error analysis of the least squares method and the constraint PSO

5 结论

变差函数拟合结果直接影响克里金插值效果，选择合适的方法拟合变差函数对于改进克里金插值效果具有较大的作用。本文在考虑地质变量特征和数据特征的基础上，将基于约束粒子群优化算法应用于变差函数拟合中，应用实测数据计算出实验变差函数值，分别利用最小二乘法和基于约束粒子群算法对其进行变差函数计算和拟合，并运用拟合结果进行二维插值，实验结果表明：基于约束粒子群优化的克里金插值算法获得的插值效果具有较高插值精度。

［1］孙洪泉.地质统计学及其应用［M］.徐州：中国矿业大学出版社，1990.Sun H Q.Geological Statistics and Its Application［M］.Xuzhou：China University of Mining and Technology Press，1990.（In Chinese）

［2］严华雯，吴健平.加权最小二乘法改进遗传克里金插值方法研究［J］.计算机技术与发展，2012，22（3）：92－95.Yan H W，Wu J P.Research on genetic algorithm Kriging optimized by weight least square［J］.Computer Technology and Development，2012，22（3）：92－95.（In Chinese）

［3］邵才瑞，印兴耀，李洪奇，等.储层属性的遗传神经克里金插值方法及其应用［J］.中国石油大学学报：自然版，2007，31（5）：35－40.Shao C Y，Yin X Y，Li H Q，etal.An integrated genetic-neural-Kriging interpolation method for reservoir property and its application［J］.Journal of China University of Petroleum，2007，31（5）：35－40.（In Chinese）

［4］Gringarten E，Deutsch C V.Teacher's aide variogram interpretation and modeling［J］.Mathematical Geology，2001，33（4）：507－534.

［5］乔金海，潘懋，金毅，等.基于Kriging方法的天然地基承载力三维模拟及分析［J］.北京大学学报：自然科学版，2011，47（5）：812－818.Qiao J H，Pan M，Jin Y，etal.3Dmodeling and analysis of natural foundation bearing capacity based on Kriging method［J］.Acta Scientiarum Naturalium Universitatis Pekinensis，2011，47（5）：812－818.（In Chinese）

［6］Park J J，Shin K I，Lee J H，etal.Detecting and cleaning outliers for robust estimation of variogram models in insect count data［J］.Ecological Research，2012，27（1）：1－13.

［7］Clark R G，Allingham S.Robust resampling confidence intervals for empirical variograms［J］.Mathematical Geosciences，2011，43（2）：243－259.

［8］颜辉武，祝国瑞，徐智勇，等.基于Kriging水文地质层的三维建模与体视化［J］.武汉大学学报：信息科学版，2004，29（7）：611－614.Yan H W，Zhu G R，Xu Z Y，etal.Volume rendering and 3Dmodeling of hydrogeologic layer based on Kriging algorithm［J］.Geomatics and Information Science of Wuhan University，2004，29（7）：611－614.（In Chinese）

［9］Krohling A K.Gaussian swarm：A novel particle swarm optimization algorithm［C］//Proceedings of the 2004IEEE，Singapore，Conference on Cybernetics and Intelligent Systems，2004：372－376.