一种复合问题的多重数字签名方案
曹 阳
(陕西理工学院 数学与计算机科学学院,陕西 汉中723000)
数字签名是实现网络身份认证、不可否认性、数据完整性等信息服务的基础,也是实现电子商务、电子金融等的重要技术保证。所谓数字签名就是接收方能够向第三方证明其收到的消息的真伪性而采取的一种加密措施。多重数字签名[1]就是多个签名者对同一份文件进行签名。Harn在1994年首次提出了一种基于离散对数难题的多重数字签名方案[2],但该方案不能用于多重数字签名。随后大量的学者提出了基于公钥密码[3]系统的多重数字签名方案,如:Lyu Wanli、卢鹏菲、胡越梅等提出了基于椭圆曲线多重数字签名方案[4-7];焦阳等提出基于ELGamal型的有序多重数字签名方案[8];罗丽平等提出了基于RSA的多重数字签名方案[9]。无论多重数字签名方案基于ECC、RSA,还是离散对数问题,最终的目的都是为了提高签名的安全性及效率[10-12]。鉴于此问题,本文通过参数替换避免求逆运算对椭圆曲线数字签名算法(ECDSA)进行改进,结合椭圆曲线密钥短、存储开销小等特点,提出一种复合问题的多重数字签名方案。
1 ECDSA快速签名方案
ECDSA的签名方程一般为xk=y+dz(modq),对系数(x,y,z)进行转换可以得到不同的签名算法,由签名方程求出v,形成签名信息(u,v)。G是椭圆曲线的基点,l是私钥,L是公钥,用(1,Mu+v,1)置换(x,y,z)则得到的签名方程和验证方程如下
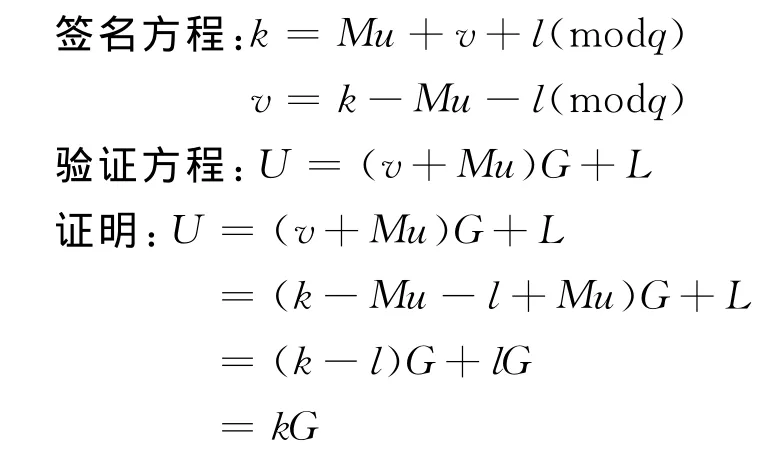
使用转换后的签名方程得到的方案如下:
(1)签名者Q在椭圆曲线上选择私钥l,G为基点,L=lG,M=hash(m),并将M转换为整数。
(2)Q随机选取整数k∈[1,q-1],并计算U=kG=(x1,y1),并将x1转换为整数,u=x1(modq),如果u=0则转第(2)步。
(3)计算v=k-Mu-lmodq,如果v=0则转第(2)步,(u,v)作为对消息m的签名,将(u,v,m)传送给验证者。
(4)验证者获取公钥L,验证u和v是[1,q-1]间的整数,计算M=hash(m),R=v+Mu(modq),如果R=0,则签名无效,否则计算U=(R+l)G=RG+L=kG=(x2,y2),u'=x2(modq),如果u′=u则签名验证成功。
签名过程中避免了求逆运算,所以签名的效率比较高。
2 复合问题的多重数字签名方案
2.1 系统初始化
设有n个签名者 {Q1,Q2,…,Qn}对同一个消息m进行签名,可信秘钥生成中心KGC生成系统参数(Fp,E,G,q,a,b,hash(),N),其中Fp为有限域,E是Fp上的椭圆曲线,G是E上的基点,q是E的阶,a和b是曲线E的系数,hash()为单向哈唏函数,N是签名重发的次数。
2.2 秘钥生成和分配
为了防止组内成员内部的欺诈行为,签名者的私钥由签名者自己生成,用户的身份以密文的形式传送给KGC,并利用离散对数难解性证明来验证用户身份的安全性。KGC为每一个签名者生成一个秘密数,将该秘密数与用户的身份简单复合后传送给每一个签名者,签名者收到后利用自己的私钥和身份解出秘密数。
(1)KGC随机选择一个整数s作为自己的私钥,计算S=sG,并公布S和G。
(2)签名者Qi(i=1,2,…,n)计算Di=Sdi,di为签名者的身份,将Di发送给KGC,KGC利用私钥解密用户身份,并为用户建立档案,将其定为合法的签名者,签名者Qi随机选择一个整数li作为自己的私钥,Li=liG为公钥,公开Li。
(3)KGC为每个签名者Qi选择随机数ki,保密,计算计算u=KG=(x0,y0),并将x0和y0转换为整数,M=hash(m+x0+y0),w=c0G,用Qi的公钥加密w得w′,根据签名者的身份将w′和ri发送给签名者Qi,公开u和M。
(4)签名者Qi利用自己的私钥li解密w,利用身份di求出ki,ci=w+Li。
2.3 签名生成
签名中心对签名者设计一种签名顺序(Q1,Q2,Q3,…,Qn,Q),最终签名由Qn提交给验证者Q,顺序发送给每一位签名者,签名中心确定发送的消息m,计算M=hash(m+x0+y0,T),公开M,然后用Q1的公钥L1加密m得m′发送给Q1,并把时间标志T发送给每一个签名者和验证者,要求签名者Qi在给定的时间ΔTi内签名,以防止签名重播。
(1)签名者Q1首先利用自己的私钥l1解密消息m′得m,计算T1=T+ΔT1,若消息m在T1时刻之前到达,M=hash(m+x0+y0,T)。若等式不成立,则Q1请求签名中心重发消息,若消息m在T1时刻还没有到达或重发的次数>N,向签名中心发送一个签名失败消息;若等式成立,则进行以下操作

公开u1和v1,利用Q2的公钥L2加密m得m′,将签名的消息(m′,c1,u1′,v1′)发送给下一个签名者Q2。
(2)签名者Qi(i≥2)接收到签名者Qi-1发来的(m′,ci-1,ui-1′,vi-1′),利用自己的私钥li解密消息m′得m。计算Ti=T+ΔTi,若Qi-1的签名在Ti时刻之前还末到达,Qi要求Qi-1重新发送消息且发送次数≤N;若Qi-1消息在Ti之前还是没有到达,或消息重发次数>N,则Qi向签名中心发送签名失败消息。
(3)验证ci=w+Li-1,M=hash(m+x0+y0,T)是否成立,若不成立拒绝签名,并要求Qi-1重新发送消息;若成立则执行第(4)步。
(4)计算ui=kiG=(xi,yi),vi=ki-Mui-li(modq),ui′=ui-1+ui,vi′=vi-1+vi,ci=w+Li,显然由第(1)步可得出:ui′=u1+u2+…+ui,vi′=v1+v2+ … +vi,公开(ui,vi)。
(5)若1≤i<n,则Qi利用Qi+1的公钥加密m得m′,将(m′,ci,ui′,vi′)发 送 给Qi+1,执 行 第(2)、第(3)步;若i=n,执行第(6)步。
(6)Qn将(M,cn,un′,vn′)发送给签名验证者Q完成签名验证。
2.4 签名验证
验证者Q收到最终签名执行以下操作:
(1)判断un和vn是[1,q-1]的素数,计算Ri=vi+Mui(modq)。
(2)查询签名者Qi(i=1,2,…,n)公钥Li和部分 签 名(ui,vi),验 证li)G(modq)。
2.5 签名验证过程的正确性证明
证明:
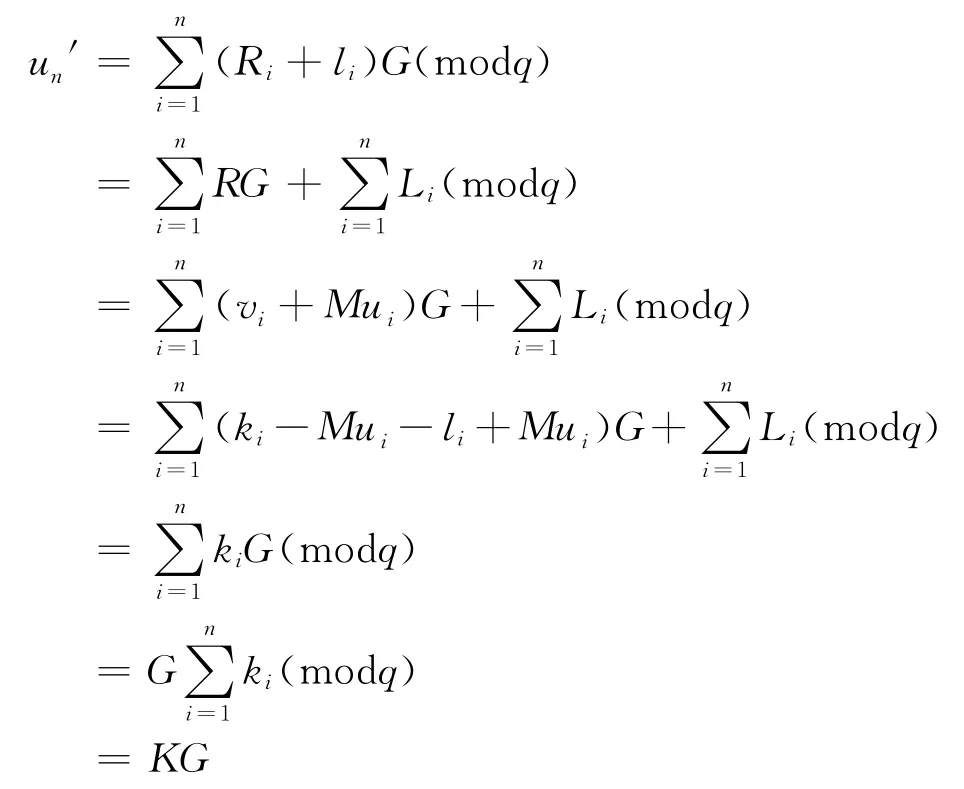
所以,上述签名验证过程是正确的。
3 安全性分析
(1)方案的安全性基于离散对数求解的困难性及签名者的身份。方案中合法签名者秘钥的生成是由自己生成,签名者向KGC提供的身份di是由KGC的公钥进行加密Di=Sdi。由Di=Sdi,S=sG知,攻击者无法知道KGC的私钥s,也就无法知道签名者的身份di,难解性基于椭圆曲线离散对数问题。若攻击者要想从签名者Qi的公钥Li解出私钥li,且想从公开的u解出K和ki,由知,要求出ki就必须知道用户的身份di,难解性仍然是基于椭圆曲线离散对数问题。
(2)本方案中消息m的传递及w的传递都是以密文的形式传递,秘密数ki与签名者Qi的身份di进行简单复合,保证了消息和ki的机密性。签名过程中,攻击者无法从vi=ki-Muili(modq)中求出vi,因为签名方程中有ki和li两个未知数,无法求解,从而保证了签名的机密性。
(3)引入时间戳防止重放攻击。M=hash(m+x0+y0,T),T为签名时间,即使攻击者获取了(M,T,ci,ui′,vi′),并将T改为当前时间,但vi-1中的M无法修改,因此不会成功。
(4)方案中设定常数N作为签名不正确时重发签名的次数,签名生成的第(3)步不成立,在时间ΔTi内,Qi要求Qi-1重新发送签名消息且发送次数≤N。从而限制攻击者尝试的次数,增强了系统的安全性。
(5)方案简化了签名验证的过程,Qi并没有将(m′,ci,ui′,vi′)广播给其后的所有签名者,只是将签名发送给其后的一个签名者,所以Qi只需验证Qi-1的签名并签名,提高了签名效率,降低了通信成本。签名时只有n个签名者的签名才是有效的,验证者验证签名时使用了签名者部分签名和公钥,有效防止中间人的攻击及恶意攻击。
4 结论
本文对椭圆曲线签名方案进行改进,避免了求逆运算,在此基础上结合椭圆曲线密码体制密钥短、安全性高等优点,提出了一种复合问题的多重数字签名方案,并分析了该方案的安全性。实现中,如果椭圆曲线上点的运算采用多标量乘运算,效率可以提高10%~20%。因而本方案在实际生活中具有一定的实用价值。
[1]Wu Z C,Chou S L.Two-base multi-signature protocols for sequential and broadcasting architectures[J].Computer Communications,1996,19(9/10):851-856.
[2]Harn L.Group-oriented(t,n)threshold digital signature scheme and digital multi-signature[J].IEEE Proceedings on Computers and Digital Techniques,1994,141(5):307-313.
[3]Harn L.Public-key cryptosystem design based on factoring and discrete logarithms[J].IEEE Proceedings on Computers and Digital Techniques,1994,141(3):193-195.
[4]Lyu W L,Zhong C.A robust elliptic curve digital multi-signature scheme[J].Computer Engineering,2004,30(5):30-32.
[5]卢鹏菲,詹雄泉,洪景新.基于椭圆曲线的有序多重数字签名方案[J].厦门大学学报:自然科学版,2005,44(3):341-343.Lu P F,Zhan X Q,Hong J X.The elliptic curve sequential multi-signature digital scheme[J].Journal of Xiamen University(Natural Science),2005,44(3):341-343.(In Chinese)
[6]胡越梅,朱艳琴.一个基于ECC的多重数字签名方案[J].微电子学与计算机,2007,24(1):180-182.Hu Y M,Zhu Y Q.An elliptic curve digital multisignature scheme[J].Micro-electronics &Computer,2007,24(1):180-182.(In Chinese)
[7]Koblitz N.Elliptic curve cryptosystems[J].Mathematics of Computation,1987,48(177):203-209.
[8]焦阳,傅德胜.基于ELGamal型的有序多重数字签名方案[J].四川大学学报:自然科学版,2013,50(4):757-759.Jiao Y,Fu D S.A sequential multi-signature scheme based on ELGamal[J].Journal of Sichuan University(Natural Science Edition),2013,50(4):757-759.(In Chinese)
[9]罗丽平,施荣华,刘宇.基于RSA的ELGamal型有序多重数字签名方案[J].计算机工程与应用,2006,42(1):120-121.Luo L P,Shi R H,Liu Y.ELGamal type sequential digital multi-signature scheme based on RSA[J].Computer Engineering and Applications,2006,42(1):120-121.(In Chinese)
[10]曹素珍,王彩芬.基于离散对数问题的可截取签名方案[J].计算机工程,2013,39(4):132-136.Cao S Z,Wang C F.Content extraction signature scheme based on DLP[J].Computer Engineering,2013,39(4):132-136.(In Chinese)
[11]王泽成.基于身份数字签名方案的通用可组合安全性[J].计算机应用,2011,31(1):118-122.Wang Z C.Universally composable security of identity-based signature schemes[J].Journal of Computer Applications,2011,31(1):118-122.(In Chinese)
[12]刘晓川,陈恩红.基于椭圆曲线的结构化多重数字签名方案[J].计算机应用与软件,2010,28(8):295-297.Liu X C,Chen E H.A structured multi-signature scheme based on elliptic curve cryptosystem[J].Computer Applications and Software,2010,28(8):295-297.(In Chinese)

