数学方法在油气田开发中的应用

韩 珊

(中国石油大学〔北京〕石油工程学院 北京 102200)

数学方法在油气田开发中的应用

韩 珊

(中国石油大学〔北京〕石油工程学院 北京 102200)

本篇文章主要介绍了模糊数学方法、最优化方法和BP神经网络数学方法原理及实例，并分析了它们在油气田开发中的利与弊。

模糊数学；最优化控制；误差逆传播网络；模型

油气田开发是依据详探成果和必要的生产性开发试验，在综合研究的基础上对具有工业价值的油气田，制订出合理的开发方案并对油气田进行建设和投产，使油气田按预定的生产能力和经济效果长期生产，直至开发结束。

在油气田开发中，油田评价尤为重要，而想要正确快速的评价一块油田，所采用的数学方法更加重要。

1 成熟数学方法应用及实例

1.1 模糊数学方法

1.1.1 原理

模糊数学方法是用数学方法研究和处理具有“模糊性”现象的数学。模糊性主要是指客观事物差异的中间过渡界线的“不分明性”，如储层的含油气性、油田规模的大小、成油地质条件的优劣、圈闭的形态、岩石的颜色等。应用模糊数学的综合评判理论评价和优选油气田开发方案，所得结论是客观的、合理的，已经在石油工业中得到广泛应用。

1.1.2 应用实例

大庆油田萨南开发区萨东过渡带300m地区，一、二、三条地区基础井网，1968年投产，采用井距为300m的四点法面积井网布井，开采层位萨尔图、葡萄花油层，两个油层为统一压力系统，平均原始地层压力为11.82MPa，原始饱和压力为10.15MPa，边、底水不活跃，开发面积为6.7km2，地质储量为1638×104t。

参考黄炳光、唐海研究成果，建立如下水驱开发效果的综合评价指标体系：根据储量控制程度、储量动用程度、能量保持水平、剩余可采储量的采油速度、含水率、存水率、注入孔隙体积、年产油量综合递减率等8项指标对水驱开发效果影响的重要程度，由层次分析法确定出相应的权重系数。

结合该8项评价指标的评价结果，利用模糊数学综合评判法确定出该区块的水驱开发效果评价矩阵为：(0.338，0.235，0.107，0.070，0.070)。根据最大隶属度原则，确定出该区块基础井网的水驱开发效果属于“好”的评价范围。

1.2 最优化方法

1.2.1 原理

1986年RaphadAmit建立了一个最优化控制模型，研究一次采油、二次采油开采中某些决策问题。目标函数为整个开发阶段的累积净现值最大，控制变量为钻井策略、井口装置策略、一次采油转向二次采油时间、二次采油阶段的采油速度和持续时间，通过最优控制问题解存在的必要性条件，得到了实现最佳开发效果的定性决策及其影响因素。

1.2.2 应用实例

国内某中后期油田1998—2007年的历史数据在一定程度上反映了其开发动态规划规律。首先运用功能模拟原理建立油田各项构成产量与其对应影响因素的关联关系，得出产量与因素的预测值，再对规划模型进行求解，可以得出油田未来多年内的各项产油量及对应的操作成本的规划结果（表1）。

表1 油田未来多年规划结果

根据规划结果以及确定出的年利率r、税率7V和未来多年的各项影响因素的预测值，可以得到该油田多年规划模型中的最大效益模型的最优值。

1.3 误差逆传播网络

1.3.1 原理

误差逆传播网络(Back Propagation，简称BP网络)。典型BP网络是3层前馈阶层网络，即输入层、隐含层和输出层各层之间全连接。对于每一层间的连接权值都可以通过学习来调节，基本处理单元(输入层单元除外)为非线性输入、输出关系(一般选用S型作用函数)，其中处理单元的输入、输出值可连续变化。

近年来，神经网络方法在油气田开发领域得到广泛应用。其优越性在于简单明了，能描述油田开发的整个过程，还可以把影响动态预测指标的各种因素自行组织起来，建立起一个广义的、准确的动态预测模型。在此基础上分别对高产、中产和低产气井压裂施工参数进行了优化设计，得到了最优的排量、液量、砂量、砂比、液氮量等施工参数，气井平均增产幅度为15.9%。结果表明优化的施工参数可以用来指导气井压裂施工，有利于提高气井的压裂效果。温庆志等人曾结合气井压裂参数，建立了压裂气井产能仿真模型，并应用该仿真模型预测了不同岩性参数、电性参数、工程参数的压裂气井产能，平均误差为0.03%，表明仿真模型准确可靠。

1.3.2 应用实例

某气田利用该方法建立了该气田单井无阻流量预测模型，利用实测的10井次资料对新模型进行检验，其计算结果与实际测试情况较吻合。

综合该地区新井的储层物性和开采状况资料，利用建立的预测模型对5口新井进行了产能预测，其结果见表2。

这个产能预测方法预测精度较高，计算速度快，使得产能预测的可信度大大提高。

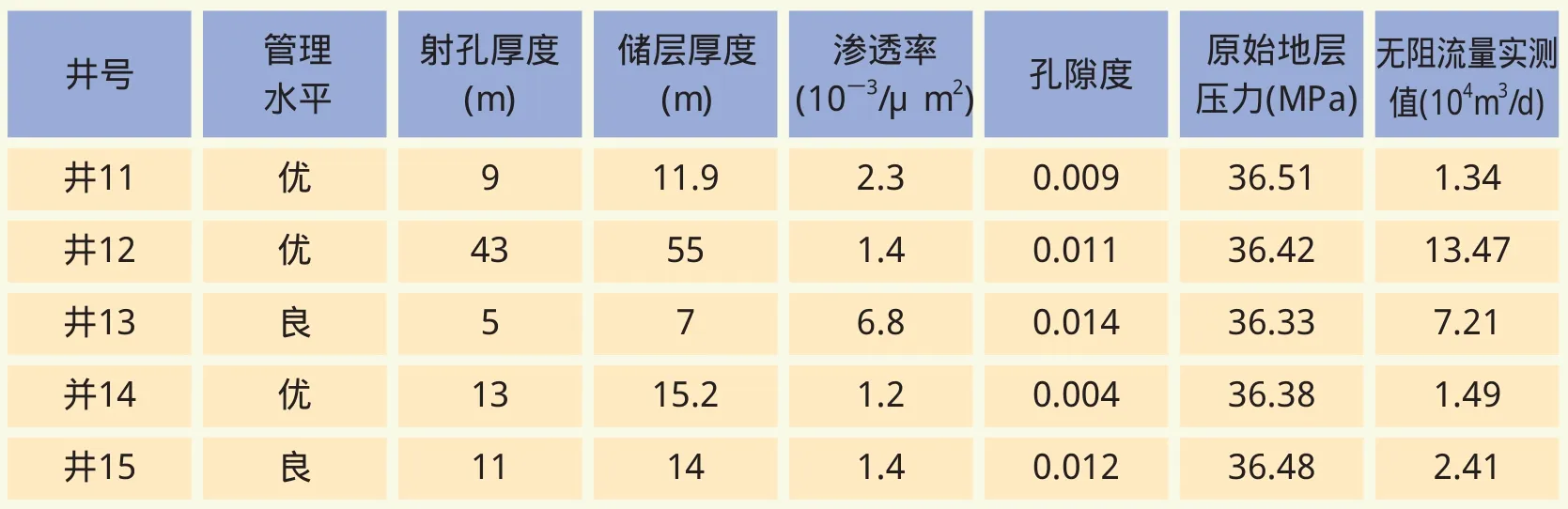
表2 某气田新井无阻力流量预测成果

2 发展前景

(1)模糊数学法可以对模糊性的信息资料做出较为科学合理，其结果包含的信息丰富，并且可避免过多的人为干扰，提高其准确性和可靠性。但不能解决评价因素之间的相关性造成的评价信息重复问题，计算较为复杂，对指标权重的确定主观性较强。

(2)最优化方法解决了很多工程技术中的实际问题，应用性较强，是能够发掘出问题的稀疏性和特殊的数据结构来处理大规模问题的快速算法。所以，它在油气田开发中的运用前景非常广阔，也吸引了越来越多研究人员的注意。

(3)神经网络具有对先前知识的学习能力和对复杂环境及其变化的适应特性，预测结果可以较好地逼近实际值，同时神经网络的信息利用能力很强，将人工神经网络用于油田产量预测取得了很好的效果，对油田的开发具着重要指导意义。

3 结论

这3种数学方法在油气田开发中都有重要的指导意义，应用前景也非常广阔。但每种方法都有利弊,必须要根据实际情况来选择采用哪种方法：神经网络建模技术应用于油田生产预测，可建立全油藏范围的生产预测模型，有建模成本低、应用范围广、不受开发阶段和开采方式的限制的特点；最优化方法的计算量比较大，但能准确的求出可行解与最优解，有很好的发展前景；BP神经网络法在预测精度与趋势方面比较可行，可以较好地解决油气田开发中的问题。

[1]马立平，任宝生，刘志斌.最优化方法及其在油田开发规划中应用综述[J].石油规划设计，2009，20(5)：10-14.

[2]张广杰，常毓文，曲德斌，董伟宏.油田开发五年（滚动）规划的逐年实施方法研究[J].石油学报，2007，28(2)：79-82.

[3]赵兰水，罗东坤，最优化理论与方法在油田产量优化研究中的改进[J].技术经济，2006，25(10)：44-47.

[4]温庆志，蒲春生，刘俊邦等.基于BP神经网络的压裂参数优化设计[J].大庆石油地质与开发，2010，29(5)：125-128.