基于特征值极限分布的合作频谱感知算法

弥寅，卢光跃

(西安邮电大学 无线网络安全技术国家工程实验室，陕西 西安 710121)

1 引言

随着无线通信技术的快速发展，无线频谱资源日益紧张，下一代无线通信技术急需解决的问题就变成了怎样提高频谱的使用效率，从而进一步提高通信系统的容量和服务质量。认知无线电(CR，cognitive radio)[1]作为一种频谱再用技术，已受到普遍关注。CR通过对授权频段进行不间断的检测，当该频段空闲，即PU不通信时，CU便可以伺机动态接入该频段进行正常通信；而当该频段被占用，即PU通信时，为了避免对PU的干扰，CU必须及时退出该频段，从而保证PU正常通信。

CR应具备3种基本能力：频谱感知(SS， spectrum sensing)、决策和自适应，其中，频谱感知是CR的首要特征和核心技术。经典的感知技术[2]有能量检测(ED， energy detection)[3]、匹配滤波器检测以及循环平稳特征检测[4]等。其中最常用的ED算法实现简单，不需预知PU发射机信号的任何先验知识，但对噪声不确定度敏感，门限不易确定。匹配滤波器检测在加性高斯白噪声(AWGN)时性能最为优越，但需要同步，且需预知PU发射机信号的先验知识。循环平稳特征检测的优点是抗噪性强，但实现起来较为复杂，由于检测时间较长，从而降低了系统的灵敏度。

在认知网络中，多径衰落和阴影衰落经常造成认知节点的信噪比(SNR， signal to noise ratio)降低，而多节点合作感知[5，6]能够在低信噪比时提高频谱检测的性能。近年来，对多节点合作感知的相关研究引起了很多人的关注。文献[7]对Wishart随机矩阵特征值的极限分布进行了详尽的分析，基于大维RMT理论， Cardoso L S提出了LSC合作频谱感知算法，用特征值之比作为检验统计量[8]，判决门限使用最大最小特征值的极限值直接做近似，由此得到的算法检测性能相比ED算法有所提高，但在采样数较小的实际应用情形下性能不够理想。由此，Zeng等人提出了最大最小特征值(MME， maximumminimum eigenvalue)算法[9]，检验统计量与LSC算法一致，该算法研究并分析了最大特征值的极限分布，结合最小特征值的渐近值，从而推导出给定虚警概率条件下的判决门限，其检测性能得到明显改善，它充分考虑了实际中采样数较小的问题，这属于半渐近的理论，其性能优于渐近算法[10]。

本文采用近年来RMT的最新研究成果，利用Wishart矩阵特征值的特性[11]，在MME算法的基础上对接收信号采样协方差矩阵最小特征值的极限分布进行了分析，发现相较于最大特征值的极限分布函数，用最小特征值的极限分布进行门限确定时更加精确。在确定判决门限时，使用最大特征值的渐近值近似代替其本身，从而提出了一种 NMME合作频谱感知算法及新的门限确定方法，该算法在CU数目和采样数较少时，感知性能较好。仿真实验对门限值曲线随虚警概率的变化进行了分析，并对NMME算法的检测性能与MME算法、ED算法进行了比较，还对各算法的实际虚警率随信噪比的变化曲线进行了分析。结果显示，在低信噪比、满足给定虚警率要求时，NMME算法具有很高的检测概率，且不需预知PU发射机信号的先验知识和噪声方差，能很好地抵抗噪声不确定度的影响。

2 系统模型和MME算法

2.1 系统模型

假设认知网络中CU数目为M，每个CU的采样数为N，CU采用合作方式对PU发射机信号进行频谱检测。这里用H0表示频谱空闲，PU不存在；H1表示频谱被占用，PU存在，从而频谱感知即为二元假设检验问题[1]

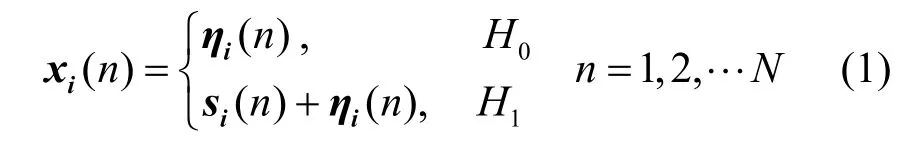
其中，xi(n)为第i个CU在第n个时刻采样到的信号向量；si(n)为第i个CU接收到的PU发射机信号向量；ηi(n)为加性高斯白噪声向量，独立同分布，均值为零、方差为σ2。

在接收端，M个CU采样得到的信号构成了一个向量矩阵X=[x1x2…xM]T，同理，S=[s1s2…sM]T，η=[η1η2…ηM]T。因此，X是一个M×N维的矩阵：

为了不失一般性，假设S与η相互独立，则在H1时，考虑CU接收信号和接收PU信号的统计协方差矩阵分别为

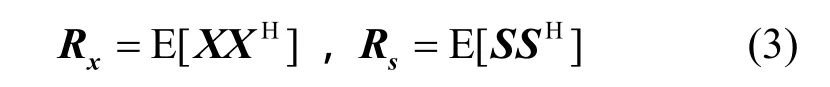
其中，H表示共轭转置变换。

容易得出Rx=Rs+σ2IM，在H0时，由Rs=0可知Rx=σ2IM。在实际的感知过程中，由于统计协方差矩阵难以准确计算，因此只能用有限的采样来估计协方差矩阵[12]，即

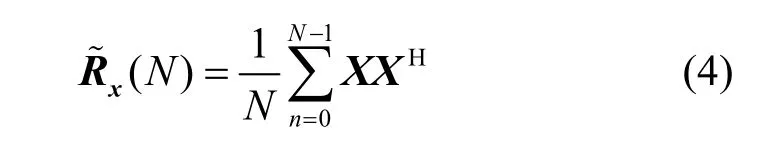
2.2 MME算法

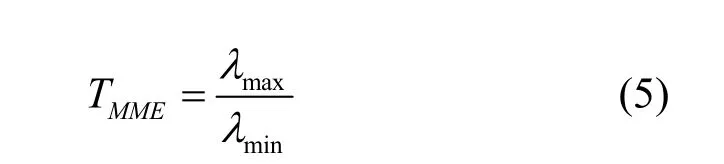
如果TMME＞γMME，表明PU发射机信号存在；否则，PU发射机信号不存在，其中，γMME表示MME算法的判决门限。

在H0时，是Wishart随机矩阵[13]，该矩阵的联合概率密度函数(PDF)极其复杂，文献[14]考虑了噪声为实信号时的情形，得出了Wishart随机矩阵λmax服从Tracy-Widom分布F1(t)的结论，文献[15]则分析了噪声为复信号的情况。当采样数N较大时，实信号和复信号时的λmax的均值和方差几乎相同，仅其极限分布不同。与此同时，文献[16]还给出了Wishart随机矩阵的最大最小特征值的收敛值。

文献[9]应用以上结论，推导出MME算法的门限表达式

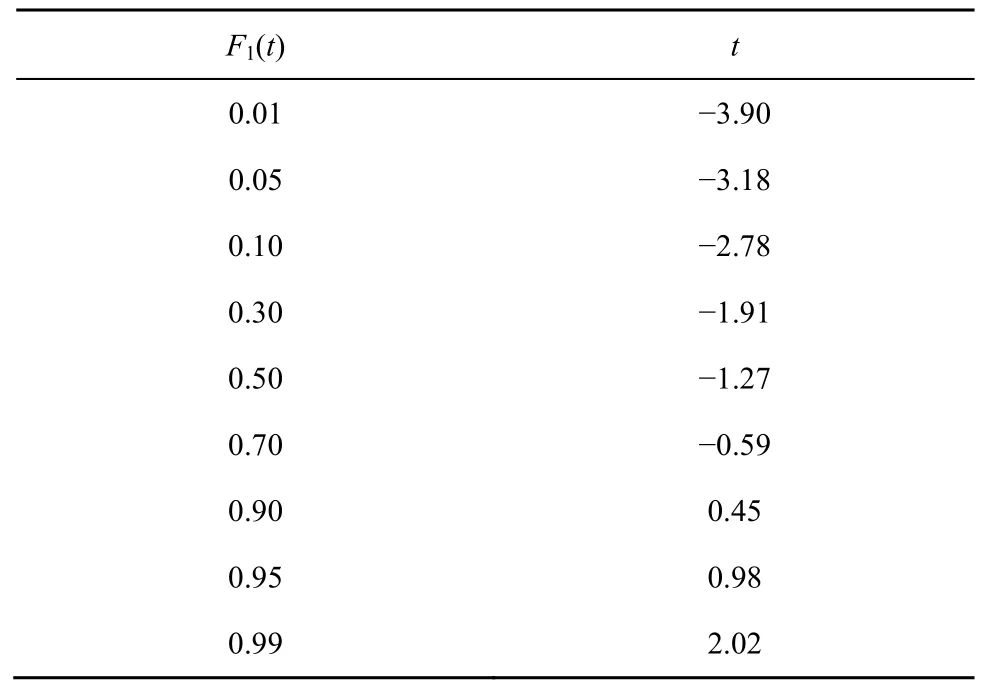
表1 Tracy-Widom第1分布的累积分布函数数值

3 改进的最大最小特征值算法(NMME)

3.1 检测门限的确定

文献[8]所提出的 LSC算法属于 RMT渐近理论，此类算法采用渐近值直接做近似，在CU数目M和采样数N足够大时才有效。而在实际应用过程中，由于各种各样的限制，如感知时间的长短、信道的时变特性等，N一般取有限值，而且LSC算法在给定虚警概率Pfa时判决门限恒定，这将会极大地影响感知系统的性能及其可靠性，因此对其应用有一定的限制。另外，在小采样时，其精度不高、误差较大，从而降低了感知的准确性。

近年来，随着 RMT的发展，发现当M和N→∞时，Wishart随机矩阵的λmin也服从 Tracy-Widom分布[7]，而且进行门限确定时，利用λmin的极限分布比目前所采用的λmax极限分布函数更加精确。

定理1[7]若噪声为实信号，令

定理1给出的是采样协方差矩阵λmin的极限分布，而定理2给出的是最大最小特征值的渐近值表达式。基于此，提出了半渐近算法，如 MME，它克服了 LSC渐近算法的缺点，能够实时地调整门限，从而提高了感知系统的性能及可靠性。下面在给定虚警概率Pfa的情况下，用λmax的渐近值近似代替其本身，推导出新的判决门限γ，由此得到的NMME算法的判决规则如下

假设噪声为实信号，则虚警概率Pfa可表示为

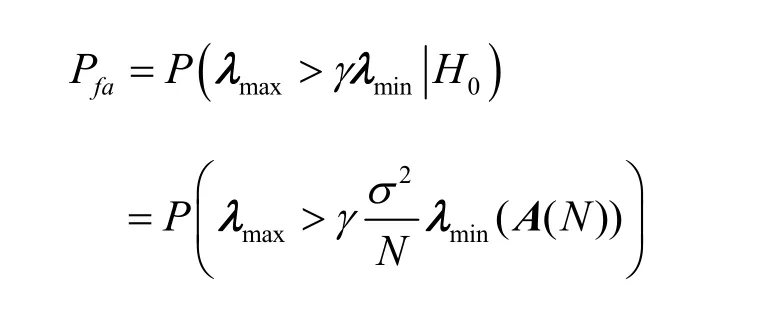
依据定理1和定理2可得b、μ和k的值。

3.2 算法步骤

综上所述，可得NMME的算法步骤如下。

步骤1对数据进行采样，并据式(4)对接收信号采样协方差矩阵(N)进行估计。

步骤 2通过对(N)进行特征值分解，求得λmax和λmin，则检验统计量TNMME=λmax/λmin。

步骤3在给定虚警概率Pfa的条件下，据式(14)求得判决门限γ。

步骤 4据式(12)进行判决，即当TNMME＜γ，H0成立；否则，H1成立。

4 仿真结果及分析

下面对算法进行Matlab仿真验证，进行10 000次Monte-Carlo实验。在给定虚警概率Pfa时，比较NMME、MME和ED算法的检测性能。假设固定路径衰落，PU发射机信号为经过升余弦脉冲成型的 QPSK调制信号；考虑噪声不确定度的影响，NMME与 MME算法的噪声不确定度为 1 dB，ED-xdB表示ED算法的噪声不确定度为xdB，估计的噪声方差为，设噪声不确定度B=max{10lgα}(dB)，α服从[-B，B]的均匀分布。

图1为不同Pfa情形下，SNR=-20 dB时，认知用户数M和采样数N对NMME与MME算法门限值的影响。参考M=5，N=3 200时的门限值曲线进行对照，M=10和N=9 600时对应的门限值都减小，说明随着M或N的增大，算法性能将会提高。同时看出，NMME算法的门限值曲线递增，而 MME算法递减。在给定Pfa的情况下，当Pfa＜0.5时，由于NMME算法的门限值更小，因此其检测性能更优；当Pfa=0.5时，曲线相交，则二者检测性能相同；当Pfa＞0.5时，MME算法有着更好的检测性能。由于实用的认知系统要求Pfa都应是较小的值，所以NMME算法的检测性能将更加优越。

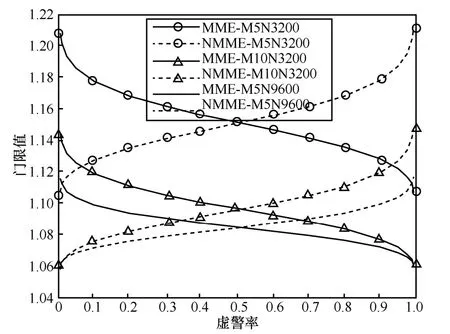
图1 NMME和MME算法的门限值曲线比较

图2是3种算法的检测率Pd随SNR变化的特性曲线。设Pfa=0.1，由图可知，如果噪声方差确知(B=0)，则 ED 算法最优。如图 2(a)所示，当SNR=-20 dB，M=5，N=3 200时，NMME算法的Pd达到52%，而 MME算法仅 2%，ED-0.5dB和ED-1dB分别为9%和5%，由此可见，实际情况中ED算法的性能远不如 NMME算法，易受噪声方差的影响。比较图2(a)和2(b)可知，M不变，N由3 200增加到 9 600，NMME算法的Pd能提高到91%，MME算法也能提高到21%。再对图2(a)和2(c)进行比较，N不变，M由5增加到10， NMME和MME算法的Pd分别提高到89%和18%。可见，增加M或N使得算法的检测性能得到了提高。同时发现，ED-0.5dB和 ED-1dB算法的性能几乎没有变化，说明通过增加M或N并不能解决噪声不确定度问题。

图3是3种算法的实际Pfa随SNR变化的曲线。设给定Pfa=0.1，N=9 600，由图可知，NMME和MME算法的实际Pfa在0.1附近，而ED-0.5dB与ED-1dB远大于0.1，不满足给定Pfa要求，造成频谱利用率低，说明存在噪声不确定度时，ED算法不够稳健。结合图2中Pd随SNR变化的特性曲线可以得出，在满足给定Pfa时，NMME算法的Pd更高。

图2 检测率Pd随信噪比变化的性能比较

图3 实际虚警率Pfa随信噪比变化的曲线

5 结束语

本文利用随机矩阵理论近年来的最新研究成果，应用更为精确的最小特征值的极限分布，并结合最大特征值的渐近值，提出了改进的NMME合作频谱感知和门限判决方法。通过Matlab仿真实验，并与MME和ED算法相比较可得，NMME算法不但是一种盲检测算法，而且不受噪声不确定度的影响。在低虚警率时，判决门限比 MME算法更低，从而在满足给定虚警率的条件下，检测概率更高，感知更加准确，体现了NMME算法的优越性。

[1] SONG M， XIN C， ZHAO Y，et al. Dynamic spectrum access： from cognitive radio to network radio[J]. IEEE Wireless Communications，2012，19(1)：23-29.

[2] YUCEK T， ARSLAN H. A survey of spectrum algorithms for cognitive radio applications[J]. IEEE Communications Surveys & Tutorials，2009，11(1)：116-130.

[3] DIGHAM F F， ALOUINI M S， SIMON M K. On the energy detection of unknown signals over fading channels[J]. IEEE Transaction on Wireless Communications， 2007， 55(1)： 21-24.

[4] 王颖喜， 卢光跃. 基于循环平稳特征的 OFDM 主用户感知的仿真研究[J]. 西安邮电学院学报， 2009，14(5)：72-76.WANG Y X， LU G Y. Primary user detection using cyclostationary properties of OFDM in cognitive radio systems[J]. Journal of Xi'an University of Posts and Telecommunications， 2009， 14(5)：72-76.

[5] ATAPATTU S， TELLAMBURA C， JIANG H. Energy detection based cooperative spectrum sensing in cognitive radio networks[J].IEEE Transaction on Wireless Communications， 2011， 10(4)： 1232 -1241.

[6] 卢光跃， 弥寅， 包志强等. 基于特征结构的频谱感知算法[J]. 西安邮电大学学报，2014，19(2)：1-12.LU G Y， MI Y， BAO Z Q，et al. The cooperative spectrum sensing algorithms based on eigenvalue structure of the received signal[J]. Journal of Xi'an University of Posts and Telecommunications， 2014， 19(2)：1-12.

[7] PENNA F， GARELLO R. Cooperative spectrum sensing based on the limiting eigenvalue ratio distribution in wishart matrices[J]. IEEE Communications Letters，2009，13(7)：507-509.

[8] CARDOSO L S， DEBBAH M， BIANCHI P，et al. Cooperative spectrum sensing using random matrix theory[A]. ISWPC 2008 3rd International Symposium on Wireless Pervasive Computing[C]. Luxem-bourg， 2008.334-338.

[9] ZENG Y H， LIANG Y C. Eigenvalue-based spectrum sensing algorithms for cognitive radio[J]. IEEE Transactions on Communications， 2009，57(6)： 1784-1793.

[10] 杨晓妮， 卢光跃. 基于特征根比分布的协作频谱感知算法研究[J].西安邮电学院学报， 2010，15(5)：5-8.YANG X N， LU G Y. Cooperative spectrum sensing algorithms based on eigenvalues ratio distribution[J]. Journal of Xi'an University of Posts and Telecommunications， 2010，15(5)：5-8.

[11] 卢光跃， 弥寅， 包志强. 特征值极限分布的改进合作频谱感知[J].信号处理， 2014，30(3)：261-267.LU G Y， MI Y， BAO Z Q. Novel cooperative spectrum sensing based on limiting eigenvalue distribution[J]. Journal of Signal Processing，2014，30(3)：261-267.

[12] LIU S L， SHEN J， ZHANG R，et al. Information on the theoretic criterion-based spectrum sensing for cognitive radio[J]. IET Communication ，2008，2(6)：753-762.

[13] TULINO A M， VERDU S. Random Matrix Theory and Wireless Communications[M]. Hanover， USA： Now Publisher Inc，2004：3-73.

[14] DIKMESE S， RENFORS M. Performance analysis of eigenvalue based spectrum sensing under frequency selective channels[A]. 2012 7th International ICST Conference on Cognitive Radio Oriented Wireless Networks and Communications(CROWNCOM)[C]. 2012. 356-361.

[15] BAIK J， BEN A G， PECHE S. Phase transition of the largest eigenvalue for nonnull complex sample covariance matrices[J]. The Annals of Probability，2005，33(5)：1643-1697.

[16] BAI Z D. Methodologies in spectral analysis of large dimensional random matrices，a review[J]. Statistica Sinica，1999，9(3)：611-677.

[17] JOHNSTONE I M. On the distribution of the largest eigenvalue in principle components analysis[J]. The Annals of statistics，2001，29(2)：295-327.