基于能量分布重叠率的海浪谱评估方法研究

张新宇 石爱国 王作超 刘 猛

（海军大连舰艇学院 大连116018）

引 言

海浪谱能够准确描述海浪能量大小与能量分布状况，是目前海浪研究的主要方向之一。在海浪谱的研究过程中，必然涉及海浪谱的评估问题。海浪谱拟合、海浪数值模拟、海浪谱估计等方法的优劣判断，包括舰船在波浪上摇荡谱的评价，最终都要通过对海浪谱的比较评估来实现。海浪谱以一系列谱密度数据的集合来刻画海浪在不同频率、不同传播方向上的能量分布，涉及到谱形的问题，其评估较一般多参数评估更为复杂。

目前对海浪谱的评估尚无统一标准和方法。常用的方法：一种是通过计算海浪参数的误差进行，一种是计算各谱密度值误差进行，两种方法均有局限性。为此，本文提出基于能量分布重叠率的海浪谱评估方法。

1 现行海浪谱评估方法

1.1 现行海浪频谱评估方法

目前频谱评估的常用方法可以分为两种：

第一种为计算研究者较为关心的海浪参数，如有义波高、谱峰频谱、谱峰值、平均周期、谱尖度等，以其误差大小作为评估指标。该方法能够直接得到使用者最关心的结果，但所得结果为多个指标，且海浪参数对谱整体形状及内部精细结构的刻画不足。一些研究者将不同海浪参数按其重要程度不同给予不同的权值，由此得到综合指标。但权值赋予往往有主观性。在实际应用中，一些参数指标在某些情况下会导致较大评估偏差。如谱峰频率指标，在双峰谱且两峰能量接近的情况下，若待评估谱与目标谱相似度很高，但因微小误差造成两频谱第一谱峰与第二谱峰颠倒，就会出现谱峰频率偏差很大，导致最终评估结果可信度降低。

第二种方法是通过计算各不同频率上谱密度值的误差得到评估结果。偏差指数（D.I.）［1-3］是较为常用的一种评估指标。

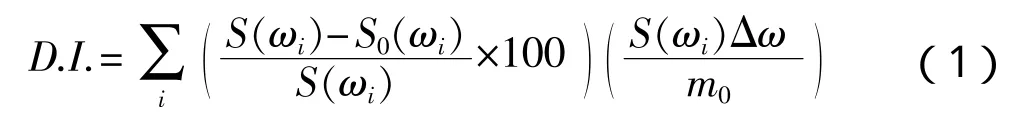
该方法可以得到单个指标，且计算过程简便客观，也是目前较普遍应用的一种方法。但该方法所得结果仅为误差的积累，相当于对各谱密度值进行单个参数处理，缺乏对海浪谱整体形状相似程度的刻画。

1.2 现行海浪方向谱评估方法

海浪方向谱为二维谱，相对于频谱的评估，方向谱的评估尚不成熟。目前常用方法的基本思路与频谱相同。

如在进行数值水池短峰不规则波实验中进行方向谱比对时，常使用有义波高、平均周期和主浪向作为指标［4-5］。其中有义波高和平均周期两指标与频谱评估相同，而使用主浪向刻画方向谱的方向分布信息是不够的。所以使用参数法进行方向谱评估尚有很大的改进余地。

文献［6］中，方向谱评估使用加权平均误差WAE（Weighted Average Error）作为评估指标［6］。

2 基于重叠能量的海浪谱评估方法

海浪谱能够刻画海浪的能量分布。因此，两种不同海浪谱的谱形重叠部分多少能够反映两者的相似程度，这与直观经验是吻合的。

2.1 海浪频谱评估方法

对于频谱而言，能量分布重叠率具体表现为两频谱重叠部分面积与两频谱所占总面积的比值。若将频谱所包围部分看作一个集合体，则重叠部分定义为两频谱集合面积交集，总面积定义为两频谱集合的并集，能量分布重叠率即交集面积与并集面积的比值，如式（3）所示。需要指出的是，本文用重叠面积（方向谱中用体积）定义的能量分布重叠率，必须在两海浪谱具有相同频率间隔的情况下才有实际意义。在实际应用中，若频率间隔不同，需使用插值方法进行调整，才能使用该数值方法。

式中：E重和E总分别代表重叠部分面积以及两海浪谱所占最大面积。和分别表示频率为时，两频谱谱密度值的最小值和最大值。EP值越大则表明两频谱越接近，当EP为1时，说明两频谱完全相同。

图1中的频谱分别为不同时刻的海上实测谱和待评估频谱［7-9］，阴影区域表示重叠部分，其中左图计算得出的EP值为0.807，右图计算求得的EP值为0.917。该方法计算简单，能够综合反映两频谱的相似程度，具有简易直观的特点，可用于一般评估，如要求更高的精度，可采用下文所述基于一阶矩的修正方法。

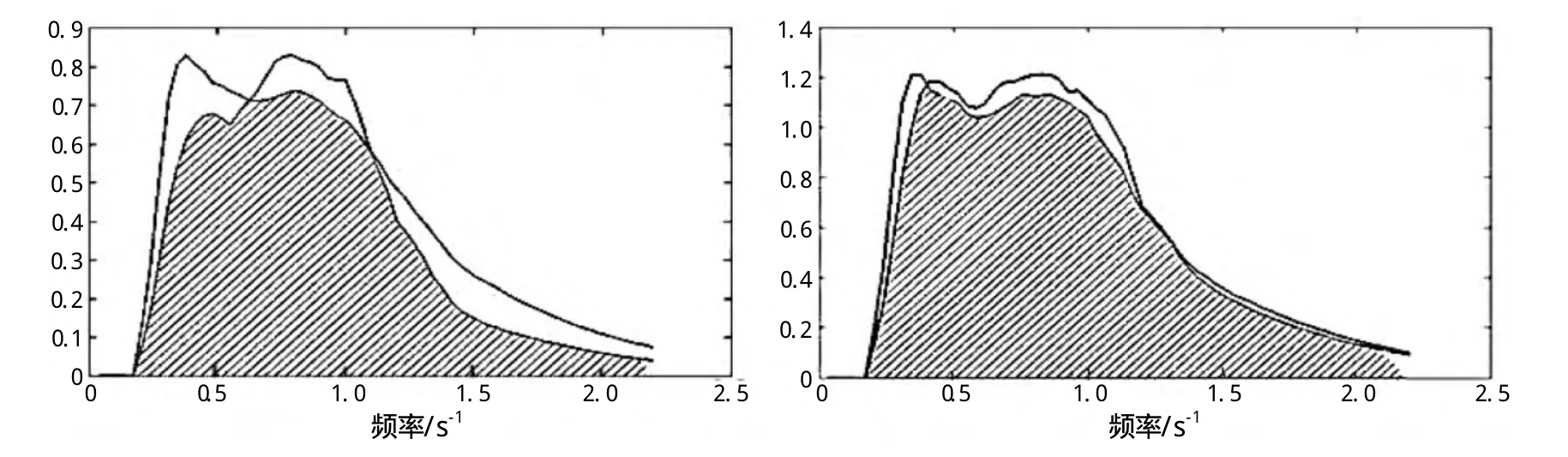
图1 能量分布重叠率评估方法效果图

2.2 基于一阶矩的修正方法

在实际评估应用中遇到如下情况：当EP值较高时，可以确定两被评估频谱相似度很高；而当EP值较低时，说明两频谱相似度较低，但无法确定两频谱不相似是由于能量大小的不同还是谱形的不同。

由于频谱的谱形代表能量分布，必须改善谱形对评估精度的影响，如图2左图计算求得的EP值为0.807 5，右图计算求得的EP值为0.807 6。两组频谱EP值基本相同，但从评估的角度，认为左图两频谱相似度更高。因此，提出基于一阶矩的修正方法（前一种方法中，面积可视为零阶矩），具体如下：

（1）首先确定重叠部分的型心位置、计算ωm，使

（2）计算基于一阶矩的能量分布重叠率

图2 谱形影响示意图

式中一阶矩取绝对值，是为避免正负值抵消。

使用该方法后，图2中左图FEP=0.808 4，右图FEP=0.710 4。从结果看，达到了区分谱形因素和能量因素比重的目的。

以上提出了对频谱进行评估的两种方法。其中，计算零阶矩的方法能较好反映两频谱的相似程度，且计算简便；计算一阶矩的方法增加了谱形因素对评估结果的影响，在重视谱形的场合评估效果更好，但计算稍显复杂。在实际应用中，可视情选择一种方法。

2.3 海浪方向谱评估方法

将上文频谱的评估方法推广到方向谱，对应的能量重叠率通过体积来计算，得到能量分布重叠率公式。

在海上采集的实际海浪方向谱，可能出现能量环形分布的情况，导致计算型心时起始点选择困难。为便于分析计算，需要略去能量方向分布很小的区域，为此可取方向扩散函数峰值的二十分之一作为阈值T，删除能量分布小于T的部分，取能量值与阈值相等的点作为起始点θ0和终止点θ1，在该范围内计算型心点θm的位置。

将基于一阶矩的能量分布重叠率法扩展到方向谱的步骤为：

（1）首先确定重叠部分的型心位置、计算ωm、dm，使

（2）计算基于一阶矩的能量分布重叠率

3 结 论

本文提出的基于能量分布重叠率的海浪谱评估方法，计算简便易行，结果直观，能够较好反映待评估谱与目标谱的相似程度。若评估中对谱形因素更为关注，则可采用基于一阶矩的能量分布重叠率法，但其计算过程略显复杂。在实际使用中可视情选择其中一法进行评估。

对于频谱评估来说，本文所述方法不失为一种实用新方法，比原有方法更加直观，有一定优势。而对于方向谱来说，由于目前所用方向谱评估方法尚欠成熟，本文所述方法则可成为一种新的选择。

［1］ 黄培基，胡泽建.胶州湾风浪频谱的拟合模式［J］.黄渤海海洋，1987（3）：1-7.

［2］ 许景波，边信黔，付明玉.长峰波海浪的数值模拟仿真与频谱估计［J］.哈尔滨理工大学学报，2010（4）：30-33.

［3］ 王虹旋，刘鹏.基于谱的海浪模拟与谱估计［J］.舰船电子工程，2012（5）：91-92.

［4］ 冯光，吴乘胜，郑文涛，等.数值水池短峰不规则波模拟研究［J］.船舶力学，2010（4）：347-354.

［5］ 张思将，杨洁，欧阳艺.基于方向谱的海浪三维数值模拟［J］.舰船电子对抗，2013（4）：54-57.

［6］ 管长龙，文圣常，张大错.分析海浪方向谱的扩展本征矢方法［J］.海洋与湖沼，1995（3）：241-246.

［7］ Nieto-Borge J C.Hessner K，Jarabo-Amores P.Signal to noise ratio analysis to estimate ocean wave heights from X-band marine radar image time series［J］.IET Radar，Sonar &Navigation，2008（1）：35-41.

［8］ Ron A，Dennix B T.Shallow water bathymetry with an incoherent X-band radar using small space time image cubes［C］//Proc.of the IEEE International Geoscience and Remote Sensing Symposium，2010：4330-4333.