关于一个重要极限的两种证明方法

程 国

（商洛学院数学与计算机应用学院，陕西 商洛726000）

0 引言

极限是高等数学中的基本概念，它贯穿于微积分始终，是研究数学问题的一个重要工具。在极限理论的学习中是一类重要的极限。关于该极限存在性的证明是一个教学难点。证明的基本思想是利用单调有界定理，即“单调有界数列比收敛”。最常见的证明思路[1-2]是将数列按二项式定理展开，证明数列{xn}单调递增有上界，再根据单调有界定理极限存在。但实际教学中，学生往往感觉这样的证明比较抽象，过程不简洁，难以理解。不少学者对此进行了研究。崔德旺[3]等利用几何均值不等式给出了存在性的一种简洁证法。杨华[4]从连续性和导数定义的角度给出了重要极限的证明方法。本文给出对极限存在性的两种简洁证法。

1 预备知识

引理1[5]设实数xffgt;-1，n为正整数，则有

引理2[6]对于任意正实数α1，α2，…，αn；β1，β2，…，βn有

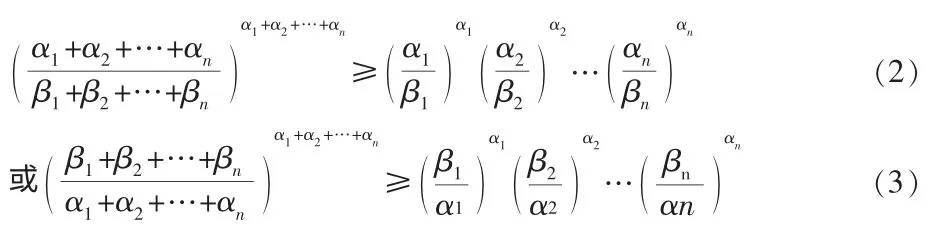
2 两种证明方法

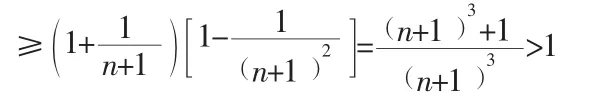
为证明数列{xn}有上界，考察数列与上面类似可证{yn}是递减的.于是即数列{xn}有上界.根据单调有界定理，得{xn}有极限.

证法2 在引理2中，当n=2时可得

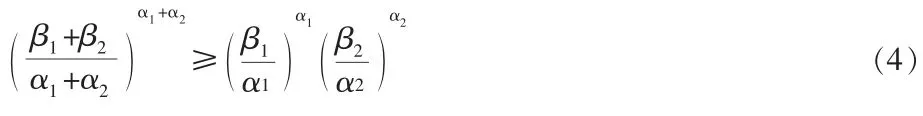
令（4）中α1=n-1，α2=1.β1=n，β2=1，则即根据单调有界原理，德{xn}收敛.

［1］同济大学数学系,编.高等数学[M].6版.北京：高等教育出版社,2007：52-53.

［2］华东师范大学数学系,编.数学分析[M].4版.北京：高等教育出版社,2006：56-57.

［3］崔德旺,何万生,夏鸿鸣,等.关于极限存在的三种新的证明[J].天水师范学院学报,2009,29(2)：9-

［5］吴新仁,陆秀丽.数学分析原理[M].北京：人民教育出版社,1979：36-40.

［6］匡继昌.常用不等式[M].济南：山东科技出版社,2004：42-43.