顺序扫描阵列配置方法研究
涂 新,朱国富,黄晓涛
(国防科学技术大学电子科学与工程学院, 长沙410073)
0 引言
MIMO阵列雷达因利用较少的阵元和较小的孔径产生较多的观测通道和较高的方位向分辨率而成为雷达领域的研究热点[1-6],阵列配置作为其中的一个重要内容而获得广泛关注[3-6]。文献[3]提出均匀且无冗余阵列的栅瓣较低、方位向分辨率很高,双程阵列的等效阵列是其收发阵列的空间卷积。因此,通常需要配置双程阵列,使其等效阵列是均匀无冗余的[4-6]。文献[4]用分解法,文献[5]用多项式因式分解,文献[6]用卷积逆运算的方法配置阵列,并在多种配置方法中选取总阵元数较少和实际孔径最短的阵列作为最优配置方法。这种阵列中,常用的是两端发射中间接收(端发多收)阵列[7]。
若端发多收阵列的阵元数较少,则其栅瓣较高[3]。抑制栅瓣可通过增加阵元来实现,但这样会增加系统成本,可以选择顺序扫描阵列解决这个矛盾[8]。普通MIMO阵列的发射阵元只发射信号,接收阵元只接收信号,而顺序扫描阵列的阵元既能发射也能接收信号,其工作方式为每个阵元轮流发射信号,其他阵元接收信号。因此,顺序扫描阵列等效阵列阵元数比端发多收阵列的多,栅瓣更低。对于这种阵列,文献[8]指出阵元的随机配置可能抑制“鬼影”(GHOST),但还没有文献进一步研究其配置问题。本文将研究这个问题,并给出一种性能较好的阵列配置方法。
1 均匀无冗余阵列配置方法分析
设阵元数为N的顺序扫描天线阵列排列于x轴上,阵元横坐标从小到大分别为 x1,x2,…,xN。在远场,等效阵列为发射与接收阵列的空间卷积[3],所以顺序扫描阵列的等效阵列是每个阵元与其他阵元的空间卷积的和。等效阵列阵元的横坐标为xk+xl,1≤k<l≤N(将xk+xl和xl+xk视为同一收发组合),权重为2,总阵元数最多可达N(N-1)/2,而端发多收阵列等效阵元数仅为2N-4。因此,顺序扫描阵列比端发多收阵列的信噪比高,能探测更远的距离,且方位向栅瓣更低。因为均匀无冗余阵列的性能较好,我们需要配置顺序扫描阵列,使其等效阵列满足这一条件。但由于得到等效阵列的方法不同,能够配置普通MIMO阵列的分解法等方法不再适用于顺序扫描阵列,下面尝试用一种新的方法配置这种阵列。
易知x1+x2是最小的横坐标,x1+x3是次小的。为使等效阵列是均匀的,不妨设x1=0且等效阵元间距为1,则 x1+x3=x1+x2+1,x3=x2+1。
若N=3,则尚未排列的最小位置是x2+x3,x2+x3=x1+x3+1,即 x2=x1+1。所以 x2=1,x3=2,构成均匀无冗余阵列。
若N≥4,则尚未排列的位置中最小的是x2+x3或x1+x4,我们分下面的步骤继续讨论。
1)假设 x1+x4>x2+x3,则 x2+x3=x1+x3+1,x1+x4=x2+x3+1,即 x2=1,x3=2,x4=4,因此能够确定的等效阵元位置为 1、2、3、4、5、6。若 N=4,等效阵列是均匀无冗余的。如果N≥5,最小的未排列位置是x1+x5。为设计均匀阵列,令x1+x5=7,x5=7。我们有如下的讨论:
(1)若N=5,则因增加x5而出现的位置是xi+x5,i=1,…,4,其值为 7、8、9、11,缺少 10,因此阵列是非均匀的。
(2)如果N≥6,x1+x6是未排列的最小位置,令x1+x6=10,即x6=10。因增加x6而新出现的位置为xi+x6,i=1,2,…,5,其值为 10、11、12、14、17。这个阵列不是均匀的,由于11出现两次,也不是无冗余的。
2)假设 x2+x3>x1+x4,则 x1+x4=x1+x3+1,x4=x2+2。若 N=4,则 x2+x3=x1+x4+1,即 x2=2,x3=3,x4=4。此时等效阵元位置是 2、3、4、5、6、7,构成均匀无冗余阵列。如果N≥5,接下来应当比较x2+x3与x1+x5。我们有如下的讨论:
(1)如果x1+x5>x2+x3,则前4个阵元的位置为0、2、3、4。此时最小的位置是 x1+x5,令 x1+x5=8,x5=8。因增加x5而出现的位置是8、10、11、12。若N=5,等效阵元位置中缺乏9,非均匀阵列。若N≥6,令x1+x6=9,x6=9。因增加 x6而出现的位置是 9、11、12、13、17。这时11和12出现两次,阵列不是无冗余的,也不是均匀的。
(2)假设x1+x5<x2+x3,用与前面相同的方法知此时阵列非均匀无冗余的。
所以,若N=3,4,上述过程给出了最优配置方法,可根据实际阵列尺寸等比例缩放阵元间距以配置阵列。但对于阵元数N≥5的顺序扫描阵列,不存在使等效阵列为均匀无冗余阵列的配置方法,第2节给出了条件弱化后的配置方法。
2 顺序扫描阵列配置方法
2.1 配置方法1
虽然第1节的结论不太乐观,但可以将条件均匀无冗余阵列弱化为均匀阵列,将对应于相同等效阵元位置的收发组合的回波数据之和归一化,则所得阵列可视为无冗余阵列,其栅瓣水平依然较低。本文方法为x1=0,x2=N-2,x3=N-1,…,xN=2(N-2),记为方法1。
易知方法1的等效阵元位置为N-2,N-1,…,4N-9,等效阵元数为3(N-2)。假设实阵列长度为L,则方法1的等效阵列长度为(3N-7)L/(2N-4),阵元间距为L/(2N-4),如图1所示。总阵元数与实阵列长度相同的情况下,端发多收阵列的接收阵元之间的间距为L/(N-2),两端的发射阵元与其相邻的接收阵元之间的距离为L/(2N-4)。因此等效阵列的长度为(2N-5)L/(N-2),阵元数为2N-4,阵元间距为L(N-2),如图2所示。

图1 方法1的实阵列及其等效阵列,等效阵列中心平移至实阵列中心
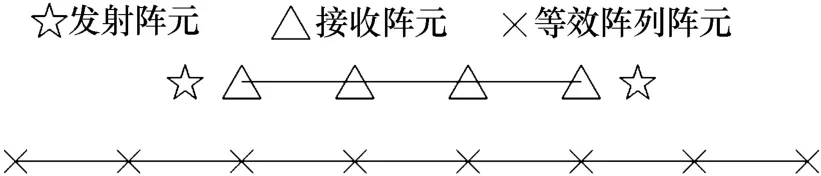
图2 端发多收实阵列及其等效阵列
假设雷达阵列发射带宽为B,最高频率为fH的步进频信号,其等效阵列是均匀的,阵元数为M,则栅瓣水平为[9]

考虑等效阵列,方法1的阵元数比端发多收阵列的多,由式(1)知其栅瓣较低;但方法1阵列长度短,约为端发多收阵列的0.75倍,因此方位向分辨率较差。
2.2 配置方法2
方法1能够配置均匀阵列,但其分辨率较差。若提高分辨率,需要进一步弱化条件,即不再约束于均匀阵列。下面设计一种非均匀阵列,其分辨率接近于端发多收阵列的。令顺序扫描阵列阵元位置与阵元总数相同的端发多收阵列相同,如图3所示,记这种配置方法为方法2。同方法1,将对应于相同等效阵元位置的收发组合的回波数据之和归一化,使其为无冗余阵列。
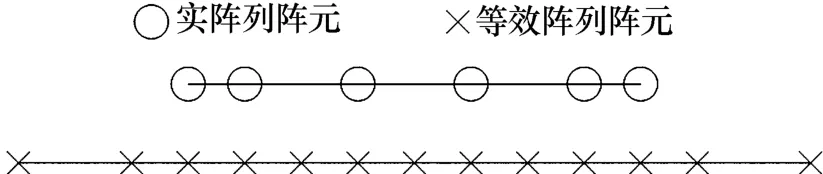
图3 方法2实阵列及其等效阵列
下面只考虑等效阵列。此时阵列长度为(2N-5)L/(N-2),阵元数为4N-11,中间4N-13个阵元的间距为L/(2L-4),最左与最右端的间距为L/(N-2)。方法2与端发多收阵列的长度相同,但前者是不均匀的,方位向分辨率较差[10]。然而当N较大时,中间4N-13个阵元构成的均匀阵列的长度逼近端发多收阵列的,因此两者的分辨率相近。方法2分辨率的计算公式见附录。由式(1)知方法2比方法1和端发多收阵列更容易达到较低的栅瓣水平。若等效阵元数较多,我们用中间4N-13个阵元估计栅瓣水平,即20lg(fH/((4N-13)B))dB。
为了验证上述对栅瓣和分辨率分析的正确性,下面对方法1、方法2和端发多收阵列进行仿真。令实阵列长度为3 m,阵列发射频率范围为0.5 GHz~3.0 GHz,步长为2 MHz的步进频信号,得到三种阵列总阵元数与栅瓣和方位向分辨率的关系,如图4所示。当N较大时,方法2与端发多收阵列的分辨率相似,而方法1的分辨率则差很多。虽然方法2的等效阵元个数比最大值N(N-1)/2少,但它的栅瓣是三种阵列中最低的,成像结果的动态范围最大。在栅瓣水平相同的条件下,方法2所需的总阵元数趋于端发多收阵列的一半,有利于减小实际阵列阵元数量并降低成本。若N≥6,方法2比方法1优越,因此第3节的设计实例只用方法2配置阵列。

图4 不同阵列的总阵元数与分辨率和栅瓣水平的关系曲线
3 配置实例
下面设计发射频率范围为0.5 GHz~3.0 GHz的步进频信号的顺序扫描阵列。我们需要确定阵元数及实际阵元位置以满足阵列前20 m处方位向分辨率为0.5 m,且栅瓣不高于-25 dB的要求。设计步骤如下:
步骤1 设等效阵列阵元个数为M,要求栅瓣不高于-25 dB,即
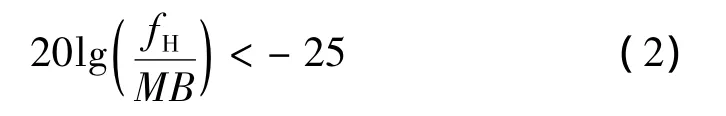
得到M≥22。所以4N-13≥22,N≥9,即总阵元数为N=9,等效阵元个数为M=23。
步骤2 方位向分辨率可以写为

令式(9)中的λ=c/fc(fc为信号的中心频率),由式(9)及M=23,得等效阵列中间的均匀子阵的阵元间距

所以实阵列长度L=(2N-4)d≈3.44 m,中间7个阵元的间距为2d=0.492 m,两端的阵元间距为d=0.246 m。实阵列及其等效阵列的阵元分布如图5所示。

图5 设计的顺序扫描阵列及其等效阵列
图6是所设计的阵列的方向图,其中栅瓣水平约为-25 dB,且方位向分辨率为0.48 m。栅瓣水平及方位向分辨率满足要求,验证了本文配置方法的有效性。

图6 配置的顺序扫描阵列的方向图
4 结束语
本文首先提出了阵元数为4的顺序扫描阵列的配置方法,但证明了若阵元总数多于4,相应的等效阵列不可能是均匀无冗余的;然后通过弱化均匀无冗余的要求提出了一种非均匀但性能较好的配置方法。理论与仿真表明,所提出的方法比端发多收阵列的栅瓣低,有利于得到更大动态范围的成像结果。
[1] 裴 英,肖文书.相干MIMO雷达关键技术研究[J].现代雷达,2013,35(3):9-12,23.Pei Ying,Xiao Wenshu.A study on key technology of the coherent MIMO radar[J].Modern Radar,2013,35(3):9-12,23.
[2] Jin T,Lou J,Zhou Z.Extraction of landmine features using a forward-looking ground penetrating radar with MIMO array[J].IEEE Transactions on Geoscience and Remote Sensing,2012,50(10):4135-4144.
[3] Schwarz J L.Ultrasparse,ultrawideband arrays[J].IEEE Transactions on Ultrasonics,Ferroelectrics,and Frequency Control,1998,45(2):376-393.
[4] Zhuge X,Yarovoy A G.Sparse multiple-input multiple-output arrays for high-resolution near-field ultra-wideband imaging[J].IET Microwaves,Antennas & Propagation,2011,5(13):1552-1562.
[5] 王 青.MIMO雷达阵列设计方法研究[D].长沙:国防科学技术大学,2011.Wang Qing.Study on approaches of MIMO radar array design[D].Changsha:National University of Defense Technology,2011.
[6] Su Y,Zhu Y T,Xu H B,et al.Multi-channel radar array design method and algorithm[J].Science China Information Sciences,2010,53(7):1470-1480.
[7] 金 添,娄 军,宋 千,等.虚拟孔径天线配置及其成像性能研究[J]. 电子与信息学报,2011,33(10):2458-2463.Jin Tian,Lou Jun,Song Qian,et al.Study on antenna configureation of virtual aperture and its associated imaging performance[J].Jouranl of Electronics & Information Technology,2011,33(10):2458-2463.
[8] Hunt A R.Image formation through walls using a distributed radar sensor array[C]//Proceedings of the 32nd Applied Imagery Pattern Recognition Workshop. [S.l.]:IEEE Press,2003:232-237.
[9] Li Z,Jin T,Chen B,et al.A coarray based MIMO array design method for UWB imaging[C] //IET International Conference on Radar Systems.Glasgow,UK:IET Press,2012:1-5.
[10] 王怀军,粟 毅,朱宇涛,等.基于空间谱域填充的MIMO 雷达成像研究[J].电子学报,2009,36(6):1242-1246.Wang Huaijun,Su Yi,Zhu Yutao,et al.MIMO radar imaging based on spatial spectral-domain filling[J].Acta Electronica Sinica,2009,36(6):1242-1246.

