基于贪心策略的EDF调度算法优化

桑 磊，陆 阳，3，俞 磊

（1．合肥工业大学计算机与信息学院，合肥230009；2．安徽中医药大学医药信息工程学院，合肥230012；3．安徽省矿山物联网与安全监控技术重点实验室，合肥230088）

1 概述

物联网技术的快速发展使得嵌入式系统被广泛地应用于物流、智能家居、安防等领域，这些嵌入式系统很多都是实时系统。实时操作系统与一般的操作系统相比，最大的特色就是其具有实时性，即：如果有一个任务需要执行，实时操作系统会马上执行该任务，不会有较长的延时，并在其截止期内完成。实时任务的这种执行时间和截止期限属性保证了各个任务的及时执行［1－2］，可见实时任务的正确性不仅取决于程序逻辑的正确性，也取决于截止期能否得到满足。

嵌入式实时系统的实时性能很大程度上取决于实时任务的调度策略。在众多实时调度策略中，基于优先级驱动（Priority Driven，PD）的算法是一类重要的调度算法，典型代表有速率单调（Rate Monotonic，RM）算法、最早截止期优先（Earliest Deadline First，EDF）调度算法等［2］。其中，EDF算法被证明是较优的动态优先级调度策略。实时系统中任务的优先级各不相同，且存在动态变化的过载状态。EDF算法在这种过载情况下会产生“多米诺效应”，一个任务错失截止期会导致后续很多任务也错失截止期，从而使得大部分任务的实时性无法保证［3］。在这种动态过载状态下，如何尽最大努力降低任务的截止期错失率（Deadline Missing Ratio，DMR）成为一个重要问题。文献［4］研究采用BACK－SLASH和SLAD算法来降低EDF调度算法在过载情况下的截止期错误率，但其以系统的复杂性显著提高为代价。

传统的实时调度算法存在的问题在于采用简单和片面的特征参数来确定优先级，如截止期、到达时间和关键性等，然而基于某个单一的特征参数不能体现任务在其他重要性方面的要求，同时也不能考虑用户对任务优先级确定的喜好［5］。为此，本文在EDF算法的基础上增加全局优先级特征参数来标识任务价值，通过引入贪心策略对过载时的任务进行最优化选择，在保证高优先级任务执行性能的前提下，尽可能地执行更多的任务，充分利用系统资源。

2 任务调度模型

2．1 算法可调度性判断

在一个单核处理器系统中，定义S＝｛t1，t2，…，tN｝为调度任务集，该任务集包含N个周期性任务，Ti表示任务ti的周期，Ci表示任务ti的最坏执行时间。

定义1（超周期） 所有任务周期值的最小公倍数，记为H。对于周期性任务，每个周期内任务的运行情况是相同的，所以，只需要分析在第一个超周期［0，H］内系统的调度情况，就可以知道在其他时段内的执行情况。在每个超周期内执行的最大任务实例数为：

定义2（周期任务的负载） 一个周期任务对处理器的平均占用率，记为Ui，Ui＝Ci／Ti，这里假设每个任务在任何时刻都是可被抢占的，且这一抢占过程不会增加其他的辅助开销。

定义3（周期任务集的负载） 系统周期任务集中所有周期任务的负载之和［6－7］，记为：

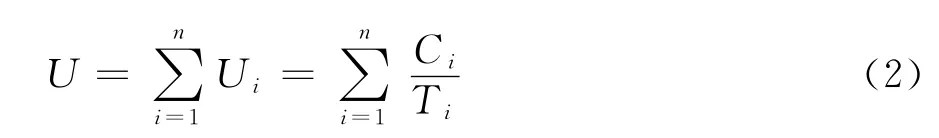
系统周期任务集的负载体现了所有任务对CPU资源的需求情况与系统能提供的最大服务之间的关系。

定理 使用EDF算法调度周期性任务集，可调度的充要条件是周期任务集的负载U≤1。

对实时系统任务集S采用EDF调度算法，当且仅当U≤1，此时系统处于低负载状态，就称任务集S是可调度的。在单处理器的情况下，在一个超周期H内，处理器忙运行的总共时间为H×U，处理器空闲的时间共为H×（1－U）。显然只有当U≤1时，才可能有一种调度算法能把所有的周期任务都执行完。但当CPU资源利用率U＞1时，会发生系统过载，任务集的处理需求大于系统的处理能力，则该任务集是不可调度的。

本文设计的算法既要保证优先级高的任务先执行，又要保证完成尽可能多的任务实例，即使任务的错失率降到最低。

2．2 贪心策略分析

在系统过载的情况下，并不是所有的任务都能执行，所以，就需要对任务有选择的进行调度，使得CPU利用率U尽可能接近于1，且被调度任务具有较高的优先级。最优调度任务集的选择过程可以抽象为一个典型的0－1背包问题。0－1背包问题可描述为：给定一个背包和n个物品，物品i的重量是wi，价值是vi。背包至多只能装下总重量为W的物品，要从这n件物品中选出若干件放入背包中，放入物品的总重量不多于W，并且背包中的物品总价值达到最大［8］。在本文最优调度集的选择问题上，就是要选择出若干任务组成最优调度集，调度集中各任务的CPU利用率U之和不超过1，且所有任务的总优先级达到最大。在过载状态下只对最优调度集中的任务进行调度，既可保证系统资源被充分利用，又可确保高优先级的任务优先被调度，这样在某个时间段内就可以提高系统性能，获得最大任务价值。

0－1背包问题是一个NP难题，而贪心算法是对0－1背包类型问题的一种常用解决方法。贪心算法是使每次所做的选择在当前看来都是最佳的，也就是期望通过所做出的局部最优选择来产生一个全局的最优解。这种启发式的求解策略并不总能获得最优解，然而在许多情况下仍能达到预期的目的。在0－1背包问题的解决上使用价值密度（价值重量比vi／wi）的贪心策略，该策略为从剩余的物品中选择价值密度最大的那个物品，使用该策略求解0－1背包问题的具体过程如下［9］：

对于每个物品，分别求出其价值密度，ri＝vi／wi，i＝1，2，…，n。

（1）按照价值密度，对所有物品按非升序排列：（v（1）／w（1））≥（v（2）／w（2））≥…≥（v（n）／w（n））。

（2）重复以下步骤，直到条件不满足为止：对当前的物品，如果重量不大于包中剩余的重量，则放入，并置物品标志为1（表明被选中），否则就停止。

算法主要耗时在于把所有物品按价值密度排序，本文是基于快速排序实现的，因此，该算法的时间复杂度为O（nlogn）。

2．3 基于贪心策略选择最优任务集选择

2．3．1 任务优先级的定义

EDF调度算法中的任务优先级是根据截止期来确定的，但是在实际的应用中，截止期短的任务并不一定是用户认为最重要的任务，而截止期长的任务也不一定是最不重要的任务，为此，在每个任务中引入一个重要程度参数Ei，来表示任务在实际应用中的重要度。已知任务Ti的运行时间是Ci，任务Ti的优先级计算如下：

其中，We和Wc分别表示重要度和运行时间的权重，且有We＞Wc。Pi越大，则优先级越大，体现出任务的价值也就越高。

2．3．2 调度算法

本文介绍了一种基于贪心策略的调度算法（EDF scheduling algorithm Based on Greedy Policy，EDFGP）。EDFGP是通过改进EDF算法而来的，EDFGP同时参考截止期和优先级2个特征参数。这里的全局优先级Pi是通过综合考虑任务的运行时间和重要度而得到的结果。这样就使得每个任务不但有截止期参数而且还拥有体现任务价值的全局优先级。

当U≤1时，系统采用EDF算法的对任务集S进行调度，系统可正常运行；当U＞1时，并不是任务集S中的所有任务都能得到调度。此时，根据任务的优先级CPU利用率比Pi／Ui，即任务的价值密度，把所有任务按照非升序排列。利用贪心策略，就能快速地从已排序的任务集中选择出一个最优任务集。系统优先对最优调度集中的任务进行调度，而只有在处理器空闲时才会对非最优调度集中的任务进行调度。

2．3．3 算法实现

EDFGP算法主要分3步实现：

步骤1用式（2）对当前系统进行可调度判断，确定系统处于过载状态，如果没有发生过载，就直接使用EDF算法调度；否则到步骤2，使用EDFGP算法进行调度。

步骤2对任务进行分类，使用贪心策略选择高价值密度的任务组成一个集合，称之为最优调度集合；而剩余的其他任务组成一个集合，称之为非最优调度集合；每当有新的任务加入时，都要重新确定最优调度集合。

图1是最优调度集的选择流程。在实际的应用中，使用链表Q用来存储最优调度集中的任务，链表P用来存储非最优调度集。选择出的最优调度集合Q必须满足式（2）中的可调度条件U≤1；而若对所有任务集S有U≤1，即系统处于非过载状态时，任务集S可以认为就是最优调度集，此时非最优调度集P为空。

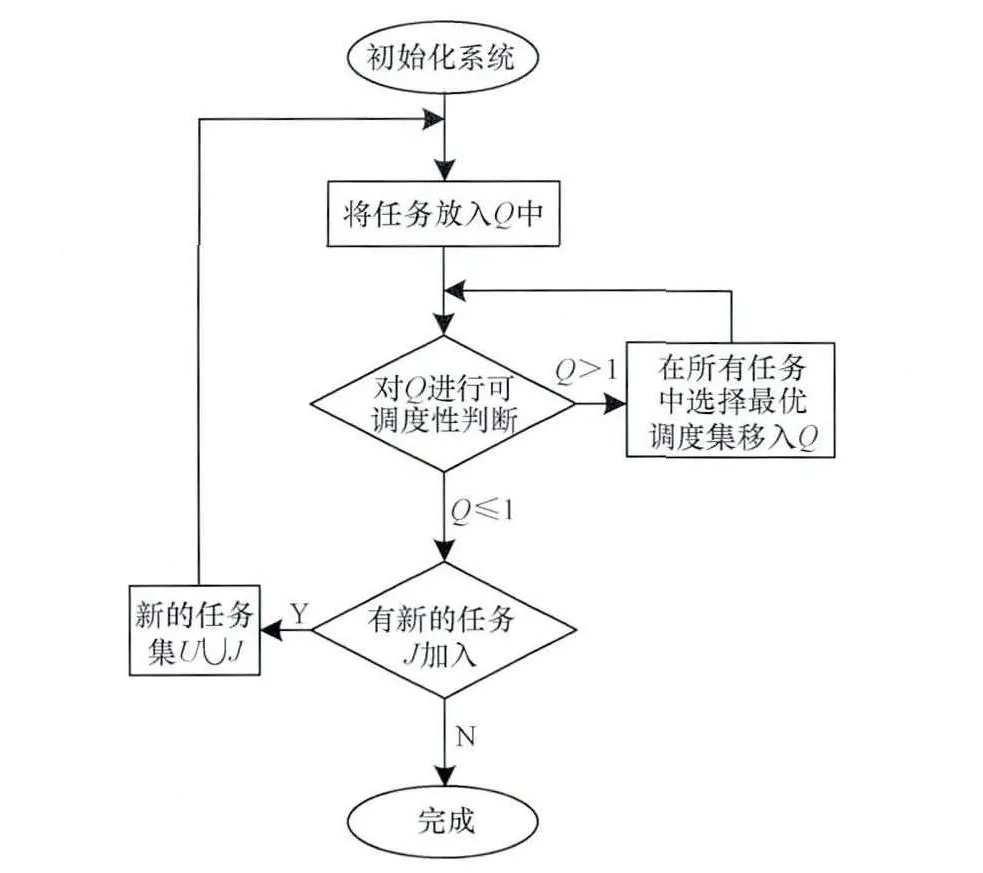
图1 最优调度集选择流程

步骤3任务调度，当前任务完成后，必须刷新所有任务的截止期，然后判断是否有新的任务加入，如果有新的任务加入，就重新使用贪心策略确定最优调度集。

EDFGP调度算法的伪代码如下：

3 性能分析与实验结果

如果一个任务不能在其截止期限内完成，则称该任务错失了截止期。在实时系统中，截止期错失率是一个评价系统性能的重要指标。DMR定义为在运行的一段时间内错过截止期的任务数与所有任务数的比值［10－11］。假设错过截止期的任务数n，而没有错过截止期的任务为m，则有：

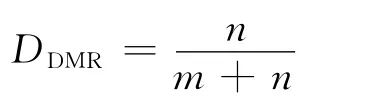
下面通过HVF，EDF与EDFGP算法的实验比较来考察各算法的执行性能。

3．1 性能分析

通过2个实验对比HVF，EDF和EDFGP算法在不同负载的情况下的性能表现。

3．1．1 低负载情况下的调度分析

设在一个实时系统中有2个任务，其周期、最坏执行时间、优先级等参数如表1所示。其中，优先级只对HVF调度算法起作用，因为在低负载时EDF和EDFGP的优先级由其任务的截止期来确定。

表1 实验任务集1

此时系统总负载U＝30／50＋10／40＋10／70≤1，系统未过载。分别使用HVF，EDF和EDFGP算法对这3个任务进行调度，运行结果如图2所示。其中，纵坐标执行性能表示不同任务的截止期被满足的比例。

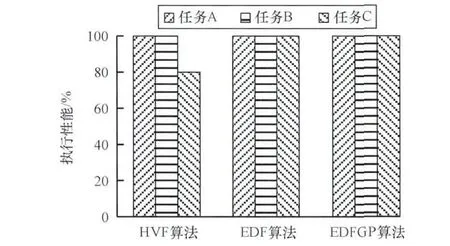
图2 系统低负载时的执行性能比较

在使用固定优先级的HVF调度算法时，任务A和任务B的DMR为0，任务得到充分执行，但任务C存在错失截止期的情况。而采用EDF和EDFGP算法3个任务都能得到有效执行，CPU资源利用率达到了100%，总的DMR为0。实验表明，在低负载情况下，EDFGP算法可以达到和EDF算法相同的执行性能。

3．1．2 过载情况下的调度分析

假设在过载情况下有3个任务，其周期、执行时间、全局优先级等属性如表2所示。

表2 实验任务集2

表2中的优先级是表示任务重要性的全局优先级，数字越小优先级越高，则此时任务价值应表示为Pi×Ui。由可调度性判断式（2）计算出CPU资源利用率为1．275＞1，即此任务集不可调度（系统过载），并不是所有的任务都能在截止期前保证完成。3个任务分别使用HVF，EDF和EDFGP算法进行调度，执行结果如图3所示。

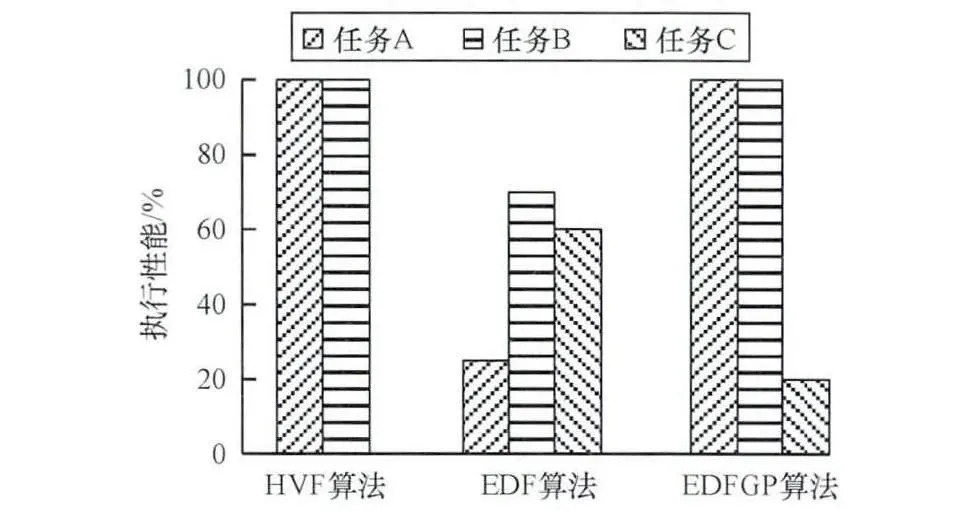
图3 系统过载时的执行性能比较

在系统过载的情况下，使用EDF算法虽然可以使每个任务都得到调度的机会，但是总体的执行性能不好，3个任务总的DMR达到了42．1%。在HVF调度算法下，只有优先级高的任务A和任务B的截止期得到了保证，优先级最低的任务C则完全错失。而在使用EDFGP算法时，既保证了关键任务A和任务B的执行，又使系统整体的DMR降低到了21．1%，调度性能比HVF和EDF算法都好。

3．2 实验结果分析

使用μC／OS－II实时操作系统对 HVF，EDF和优化后的EDFGP算法进行仿真实验，并通过实验来对比各算法的截止期错误率DMR。

参考μC／OS－II的内核结构，修改系统任务控制块模型并产生多个随机的周期性任务［12－14］，其中系统优先级设置为1～64，产生的任务数为1～64。任务的周期和执行时间同样分别在［100，700］，［1，50］区间上随机产生。分别使用HVF，EDF和EDFGP算法对这些随机生成的任务进行调度。使用μC／OS－II中的状态检查函数OSTaskStat（）可以统计出每个任务实际的完成时间，通过与该任务的截止期进行对比就可以判断是否错失了截止期，然后计算出整组任务的DMR。反复进行多组实验后，3种调度算法的DMR对比如图4所示。

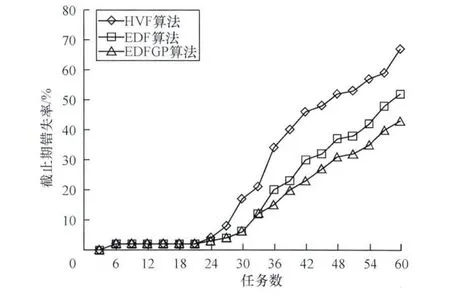
图4 3种算法的截止期错失率对比

从实验结果可以看出，3种算法在负载较低时都保持着较好的一致性，但是在任务数增加到一定程度后，3种算法都会存在任务截止期错误率急剧上升的问题。其中，HVF算法在系统过载后DMR上升最为明显，而从增加的速度上来看，EDFGP算法DMR增速较EDF算法略低；在同样的系统负载下，经过优化后的EDFGP算法的DMR要比优化前的EDF算法低。同之前的仿真性能分析比较，在未过载的情况下实验结果与前面的性能分析一致，在系统过载的情况下，EDFGP算法较HVF算法有着明显的性能提升，虽然相对于EDF算法的提高并不明显，但也达到了优化的目的。

4 结束语

本文在EDF算法的基础上，分析其在过载情况下所存在的问题，提出一种基于贪心策略的动态抢占调度算法。该算法使用贪心策略从任务集中高效地选择出最优调度集，使CPU资源得到充分利用，并实现高优先级任务的及时调度，从而降低系统的截止期错误率，提高算法的执行性能。实验结果表明，本文算法较EDF算法具有更低的截止期错失率。下一步将研究如何优化最优调度集的选择过程，使调度性能提高更为明显。

［1］夏家莉，陈 辉，杨 兵．一种动态优先级实时任务调度算法［J］．计算机学报，2012，35（12）：2685－2695．

［2］Liu C L，Layland J W．Scheduling Algorithms for Multi－programming in a Hard－real－time Environment［J］．Journal of the ACM，1973，20（1）：46－61．

［3］罗 钧，吴 志．嵌入式系统动态策略任务调度算法［J］．重庆大学学报：自然科学报，2008，31（7）：792－796．

［4］余祖峰，蔡启先，刘 明．EDF调度算法的实时性改进［J］．广西工学院学报，2010，21（1）：82－85．

［5］夏家莉，陈 辉，杨 兵．一种动态优先级实时任务调度算法［J］．计算机学报，2012，35（12）：2685－2695．

［6］程 禹，赵宏伟，龙曼丽，等．最早截止期优先调度算法的改进［J］．吉林大学学报：工学版，2013，43（5）：1338－1342．

［7］于国龙，张明富．基于桶排序的 EDF调度算法优化［J］．兰州理工大学学报，2013，39（4）：110－113．

［8］史 岚，张义宏，吕建辉，等．基于绝对贪心和预期效率的0－1背包问题优化［J］．计算机应用研究，2014，31（3）：684－687．

［9］田烽楠，王 于．求解0－1背包问题算法综述［J］．软件导刊，2009，8（1）：59－61．

［10］吴 讯，马 媛，董勤鹏．实时操作系统实时性能测试技术研究［J］．系统仿真学报，2013，9（2）：12－15．

［11］宋 杰，檀林欣，曹竹冬，等．一种新型的实时调度算法［J］．计算机技术与发展，2010，20（12）：73－76．

［12］龙昭华，漆动波，蒋贵全．一种嵌入式系统自适应调度算法研究［J］．重庆邮电大学学报：自然科学版，2009，21（5）：653－657．

［13］尹嘉鹏，徐志祥．针对少实时任务应用的嵌入式Linux改进［J］．计算机工程，2013，39（10）：49－52．

［14］周本海，王溪波，乔建忠，等．基于多参数的μC／OS－Ⅱ任务优先级和调度方法［J］．计算机工程，2007，33（21）：28－30．