Fisher判别分析法在边坡稳定性评价中的应用

■朱 敏 ■中铁时代建筑设计院有限公司，安徽 芜湖 241001

1 引言

边坡是指具有倾斜坡面的坡体，边坡是由漫长的地质作用造成的，是一个受多因素影响、随时空变异的复杂动态系统。由于坡体表面倾斜，在自身及其内外力作用下，整个坡体都有从高处向低处滑动的趋势，如果坡体内部某一个面上的滑动力超过土体抵抗滑动的能力，就会发生边坡失稳。在我国，随着城市建设的发展，近年来全国各地兴建了许多道路、铁路、高层建筑、地铁和其他地下市政设施，由此而产生了大量的边坡，并成为岩土工程的主要内容之一。边坡稳定性分析的方法很多，总的来说，大致可以分为两大类:定性分析方法和定量分析方法，其中定量分析方法又可以分为确定性分析方法和不确定性分析方法［1］。定性分析方法主要包括:自然(成因)历史分析法、图解法、边坡稳定性分析数据库和专家系统等。定量分析方法主要有:极限平衡法、数值分析法、灰色系统评价法、可靠度分析方法、模糊综合评价法、神经网络法等。对于边坡稳定性的分析和评价，单纯强调定性分析或定量评价都是难于真正解决问题的。鉴于边坡工程的稳定性分析与设计具有可变性、不确定性、没有原型和数据有限等特点以及地质环境的复杂性，边坡稳定性分析的主要目的是为了“理解机制”并非精确的定量计算。因此，在目前情况下，充分开发、挖掘和利用已被验证了的边坡的成功经验有着重要的实际意义。

判别分析法是用于判别个体所属群体的一种统计方法，其特点是根据已知类别的若干样本数据信息，总结出客观事物分类的规律性，建立判别公式和判别准则，然后对未知类别的样本进行判别分类，是一种应用性很强的统计分析方法，主要的判别分析方法有Fisher判别分析法、Bayes判别分析法、距离判别分析法等，判别分析法已在经济、医学、气象学等多个学科领域取得了很好的效果。［2］本文重点研究Fisher判别分析法分析边坡稳定性问题。分析Fisher判别分析法的基本原理，针对边坡稳定性分析建立相应的Fisher判别模型。结合具体工程实例，利用现有的数理统计分析软件SPSS，计算分析所建立的Fisher判别模型的实际适用性。利用该模型对具体边坡进行预测，通过预测结果与实际边坡状态比较，结果表明Fisher判别分析模型预测准确度高，判别性能良好，不失为边坡稳定性分析的一条新思路。

2 Fisher判别分析法

2．1 基本原理

Fisher线性判别分析(FLDA)［3］是由费舍尔于1936年提出的一种非常经典的两类问题分类技术，主要是用统计方法将待判的未知样品与已知类型的样品进行(定量)类比，综合考虑多种变量或标志，按照某种最优化判别准则作为分类基础，以确定待判样品应归属于其中哪一类。费歇判别法的思想是投影，使多维问题简化为一维问题来处理。选择一个适当的投影轴，使所有的样品点都投影到这个轴上得到一个投影值。对这个投影轴的方向的要求是:使每一类内的投影值所形成的类内离差尽可能小，而不同类间的投影值所形成的类间离差尽可能大。

2．2 判别函数及准则

2．2．1 Fisher准则

考虑指标与p个自变量有关的两类判别:设指标y按其取值范围只分为A、B两类，对A、B两类分别有nA，nB个样品数据。Fisher提出，建立p个因子的一个线性判别函数

于是，可解得线性判别函数的系数c1，c2，…，cp

2．2．3 Fisher判别标准

当判别函数求出后，可进一步求得判别临界值:

将新样品的各变量观测值代入判别函数，求得相应的函数值y(判别得分)。建立判别标准如下表:

待判样品与临界值关系当¯y(A)＞¯y(B)当¯y(A)＜¯y(B)y＞y0 归于A组 归于B组y＜y0 归于B组 归于A组y=y0待判 待判

2．3 判别效果的分析和检验

所建立的判别函数是否有实际意义，判别效果有无实用价值，准确度如何，同样需用作检验分析。实际中常用回判法来评价判别函数的有效性［3］。用所建立的差别函数对两总体的已知样本进行回判，并将判别结果，与已知结果对比，计算判错率。用n12表示将属于A类的样本误判为B类的个数，n21表示将属于B类的样本误判为A类的个数，则误判率η的回代估计为:

3 边坡稳定性分析的Fisher判别模型及应用

3．1 判别函数的建立与检验

影响边坡稳定性的因素很多，如岩土体结构、强度、地下水、工程荷载条件等等，大量工程实际及研究表明对边坡稳定性起关键性作用的影响因素有重度、粘聚力、内摩擦角、边坡角、边坡高度、孔隙水压力比等。因此本文选取以上六项指标作为边坡稳定性的影响因素，并将边坡分为稳定边坡(A类)、破坏边坡(B类)两大类［2］。选用的已知实际状态的边坡有20个，待判别的未知边坡有5个。以已知实际状态的20组边坡样本建立判别模型，应用SPSS软件对边坡的参数进行判别分析［5］。并根据判别函数，将未知状态边坡的参数带入进行判别分析，根据所得出的结果对未知边坡进行判别分类。具体数据如表1示:

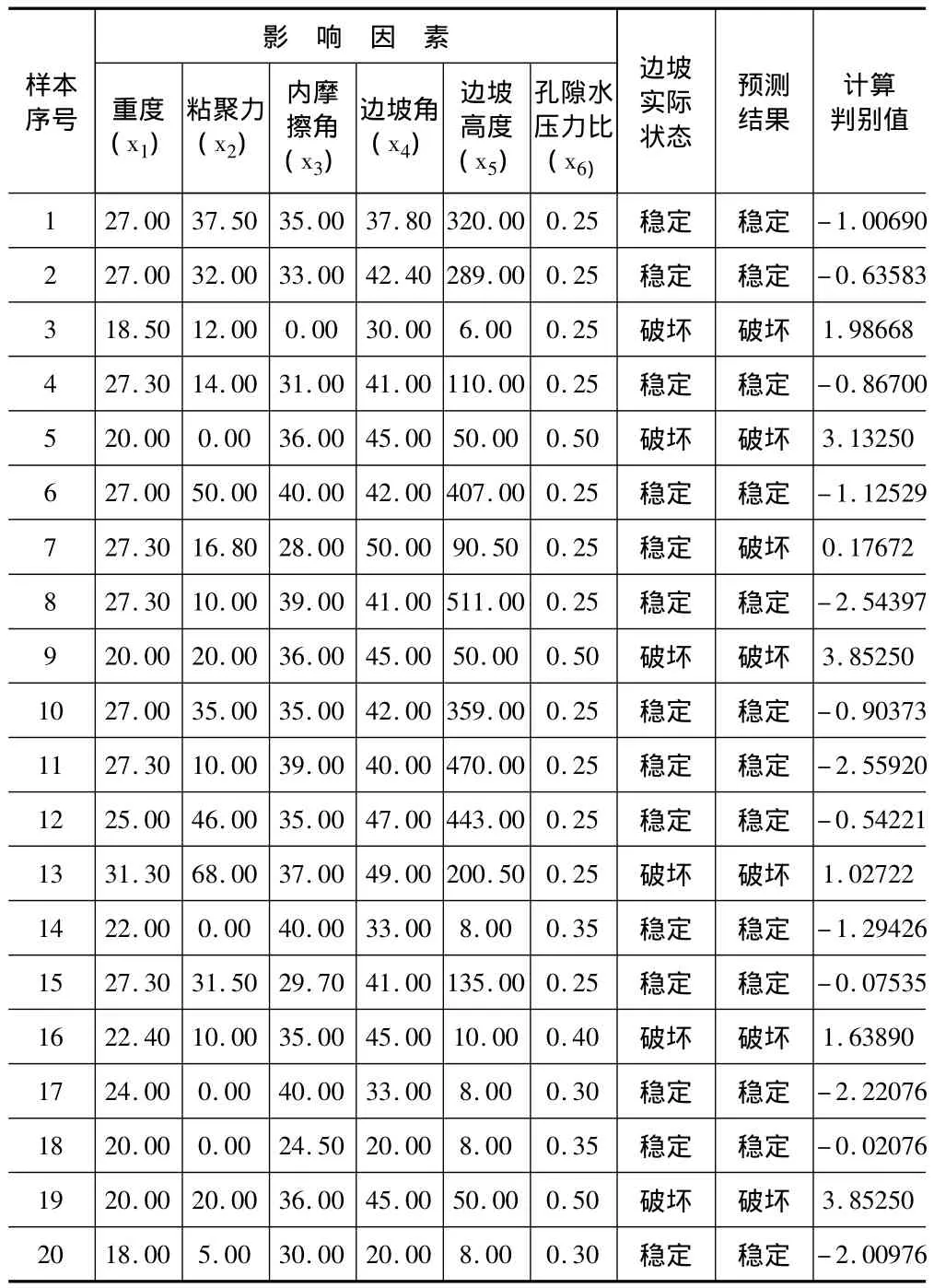
表1 边坡样本数据及计算分析结果

注:其中标注*号的为待判别边坡。

通过判别分析可得判别函数:

其中y为判别指标，C为判别变量x的系数，x为判别变量，本例中，x1-x6分别为重度、粘聚力、内摩擦角、边坡角、边坡高度、孔隙水压和孔隙水压力比。

从判别函数中可以看出，孔隙水压力的系数值最大，这表明函数对孔隙水压力值最敏感，孔隙水压力值在一定程度上能较好地反映边坡稳定性。

3．2 判别模型的校验

通过表1以看出，20个样本中只有1个根据判别式预测的结果与实际结果又差别，出现错判的样本编号为7，误判率为5%，可见利用统计学中的Fisher判别分析方法可以较好地边坡稳定的判别与分类问题，可信度高。说明所建立的判别函数的判别效果较好，可以用于对新样本的判别分类。

将待评价的5个边坡(21-25)的指标带入上述判别函数，判别结果与实际边坡状态完全一致(见表1)。说明利用Fisher判别法评价边坡稳定性是一种较为可行的评价方法。它的特点是可以利用状态已有明确结论的边坡的参数作为变量建立一系列判别函数，对边坡进行判别分析。

4 结论

边坡稳定性的分析方法理论多种多样，目前还没有很好方法去解决这一复杂问题。本文从数理统计的角度出发，将Fisher判别分析法应用到边坡稳定性的分析中，结果准确，效果好，可以运用于影响因素多而复杂的边坡稳定性分析中，同时可得出以下两条结论:

(1)建立的判别函数中，孔隙水压力的系数最大，说明判别函数对孔隙水压力值敏感，孔隙水压力能较好反映边坡稳定性分类。

(2)Fisher判别分析法依据的是统计数据，因此可以极大程度消除人为因素的影响。结合SPSS软件，使分析过程快捷简便且计算结果较为可靠准确，效率更高。

［1］宋丽娟，黄志全．边坡稳定性分析方法综述与展望［J］．山西建筑，2009，4(35):116-117．

［2］．白云飞，江露英．边坡稳定性预测的 Fisher判别分析模型［J］．有色金属，2010，2(62):49-53．

［3］李秀珍，王成华等．基于Fisher判别分析法的潜在滑坡判识模型及其应用［J］．中国地质灾害与防治学报，2009，4(20):24-26．

［4］颜可珍，刘能源，夏唐代．基于判别分析法的地震砂土液化预测研究［J］．岩土力学，2009，7(30):2049-2052．

［5］李志辉，罗平．SPSS for Windows统计分析教程［M］．第二版．北京:电子工业出版社，2005．