凸增量极限学习机的逼近阶

王 博

（西北大学现代学院 系部发展中心，陕西 西安710130）

0 引 言

人工神经网络是由大量简单的处理单元（神经元）相互连接，通过模拟人类大脑处理信息的方式，以并行、分布、协同方式完成复杂计算任务.函数逼近及泛化能力是衡量神经网络的重要性能［1-4］.前向神经网络是神经网络中一种典型分层结构，输入信号从输入层进入网络后逐层向前传递至输出层.由于它对非线性映射具有极强的模拟能力，并且对连续函数而言，前向神经网络就是一个万能逼近器，因此是迄今为止研究最为广泛的一类网络模型.

许多前向神经网络模型已在数学上证明是全局逼近的，如传统多层感知（Multilayer perceptron machine，MLP）网络［5］，RBF网络［6］，模糊网络［7］等.但是，传统的神经网络学习算法（其中最具有代表性的算法为BP算法）由于使用基于梯度的方法来训练网络，且在训练过程中要求调整网络中的全部参数，因而学习速度缓慢、易陷入局部极小.文献［8］于2006年进一步提出了“极限学习机”（Extreme learning machine，ELM），在该算法中，随机选取输入层与隐层之间的连接权重与阈值，而隐层与输出层之间的连接权重则由最小范数最小二乘解确定.采用随机选取隐变量不仅减少了网络参数设置和选择，且无需迭代的学习模式大大提高了学习速率并保证了网络的泛化能力.但是该算法需要人为通过多次实验比较误差来确定隐节点个数.使得整个训练不仅耗时，而且无法保证选取到最优的隐结点个数.在此基础上，文献［9］又提出一系列调整网络结构的新算法——I-ELM算法.I-ELM算法是通过逐个添加隐单元以逼近给定目标函数，避免了ELM算法需经过多次实验比较误差选取合适的隐节点个数的缺陷，从而表现出比原始ELM算法更优的网络结构.在I-ELM算法的进一步发展中，文献［10-11］又提出了CI-ELM算法和EI-ELM算法.CI-ELM算法采用Barron凸优化理论［12］调整输出权值，当添加新的隐单元后，重新调整已有隐单元的输出权重，使得网络结构更紧凑.理论及实验结果证明，当激活函数满足分段连续时，CIELM算法所产生函数序列可以以任意精度逼近给定的连续目标函数.但文献［10］对CI-ELM算法的逼近能力只是从定性上进行描述，而对其定量的研究并不完善.本文将基于Cauchy-Schwarz不等式对CIEL算法的逼近阶进行更进一步的分析，并给出具体的CI-ELM逼近阶.

1 凸增量极限学习机

1.1 预备知识

文中考虑具有一个线性输出节点的单隐层前向神经网络，所有的分析结果都可推广为多个非线性输出节点的情况.一个含有d个输入，n个隐节点以及一个线性输出的单隐层前向神经网络的数学模型可表示为

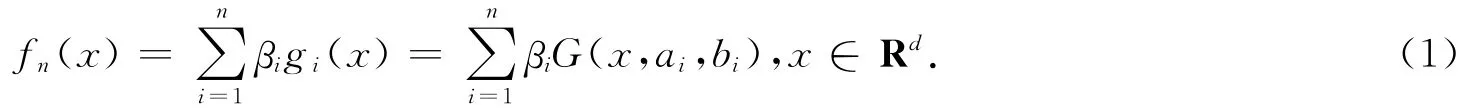
式中，ai表示输入层与第i个隐节点之间的连接权值，bi表示第i个隐节点的阈值，βi表示第i个隐节点和输出节点之间的连接权值，fn（x）表示第n步所得的网络，gi（x）=G（x，ai，bi）表示i个隐节点的输出.

单隐层前向神经网络中，通常考虑两种类型的隐节点在激活函数g（x）下的输出，这两种类型分别为

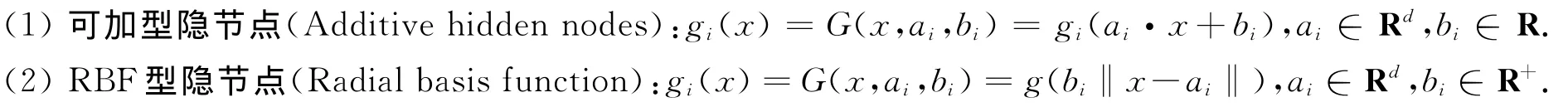
增量极限学习机的迭代公式为fn（x）=fn-1（x）＋βngn（x）.在增量极限学习机中，隐节点逐个增加，每增加一个新的隐节点gn（x）时，其对应的隐单元参数ai与bi服从某种连续概率分布随机选取，新增隐节点与输出层的连接权值βn则按照

计算，已有隐节点与输出层的连接权值则保持不变.其中en=fn（x）-f表示误差函数.

1.2 CI-ELM算法

CI-ELM是在增量学习机的基础上，结合Barron凸优化理论的一种改进算法.与I-ELM不同的是，该算法在添加新的隐单元后，已有隐单元的输出权重需要重新计算.这一改进使得所获网络结构更加紧凑且泛化能力更好.理论及实验结果表明，当激活函数满足任意分段连续时，CI-ELM所产生的网络序列可以以任意精度逼近给定的连续目标函数.其迭代公式为

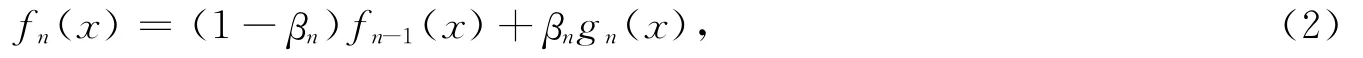
在凸增量极限学习机中，当新增隐节点gn时，所有隐节点与输出层的连接权值同时按照下述公式进行重新调整：

文献［10］中已经证明了凸增量极限学习机的全局逼近能力，具体结论如下.

引理1［8］给定可加型隐节点形式的激活函数g（x）=a·x＋b.若g（x）不是多项式函数，则span｛G（x，a，b）=g（a·x＋b），a∈Rd，b∈R｝在L2中稠密.

引理2［8］给定RBF型隐节点形式的激活函数g（x）=b‖x-a‖.若g（x）是有界可积的连续函数，则span｛G（x，a，b）=g（a·x＋b），a∈Rd，b∈R｝在L2中稠密.

定理1［9］给定任意非恒值逐段连续函数g：R→R.如果span｛g（a·x＋b）｝在L2中稠密，则对于任意连续目标函数f和任意随机产生的函数序列｛gn（x）=g（an·x＋bn）｝时，当

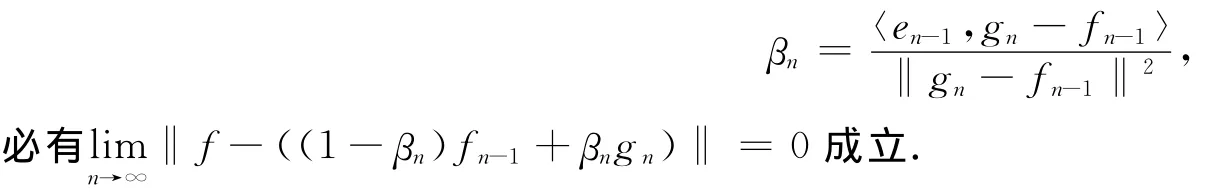
2 CI-ELM的逼近阶证明

2.1 预备知识

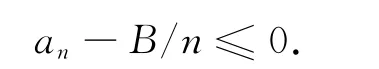
命题得证.

2.2 CI-ELM逼近阶证明

结合上式可得

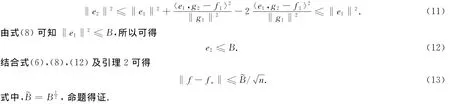
3 结束语

凸增量极限学习机是在增量极限学习机的基础上，结合Barron凸优化理论计算输出权值的一种改进算法.但对CI-ELM算法的逼近能力分析只是从定性上进行描述，而对其定量的研究并不完善.针对激活函数g（x）所生成的函数序列，定义了一个特殊的规范激活函数空间D，并在D上构造目标函数空间A1（D），利用Cauchy-Schwarz不等式给出具体的CI-ELM逼近阶为O（n-1／2）.还可以看出，对凸增量极限学习机的逼近能力的定量分析是建立在目标函数空间A1（D）上的，这使得所得结果具有局限性.因此，如何使得结果具有通用性，需要进一步的研究.

［1］ ZHANG Rui，LAN Yuan，HUANG Guangbin，et al.Universal approximation of extreme learning machine with adaptive growth of hidden nodes［J］.IEEE Transactions on Neural Networks and Learning Systems，2012，23（2）：365-371.

［2］ XU Zongben，CAO Feilong.The essential order of approximation for neural networks［J］.Science in China，2004，47（1）：97-112.

［3］ KIMK K K，PATORN E R，BRAATZ R D.Universal approximation with error bounds for dynamic artificial neural network models：A tutorial and some new results［J］.IEEE International Symposium on Computer-Aided Control System Design.Denver：IEEE，2011：834-839.

［4］ 徐柳，贺兴时.基于 HS算法的 Markov模型及收敛性分析［J］.西安工程大学学报，2013，27（6）：155-159.XU Liu，HE Xingshi.Markov model and convergence analysis based on harmony search algorithm［J］.Journal of Xi′an Polytechnic University，2013，27（6）：155-159.

［5］ BARRON A R.Universal approximation bounds for superpositions of a sigmoidal function［J］.IEEE Transactions on Information Theory，1993，39（3）：930-945.

［6］ NONG Jifu.Conditions for radial basis function neural networks to universal approximation and numerical experiments［C］／／第25届中国控制与决策会议论文集.贵阳：IEEE，2013：2193-2197.

［7］ DAI Shilu，WANG Cong，WANG Min.Dynamic learning from adaptive neural network control of a class of nonaffine nonlinear systems［J］.IEEE on Transactions Neural Networks and Learning Systems，2014，25（1）：111-123.

［8］ HUANG Guangbin，ZHU Qinyu，SIEW C K.Extreme learning machine：A new learning scheme of feedforward neural networks［J］.Neural Networks，2004（2）：985-990.

［9］ HUANG Guangbin，CHEN Lei，SIEW C K.Universal approximation using incremental constructive feedforward networks with random hidden nodes［J］.IEEE Transactions on Neural Networks，2006，17（4）：879-892.

［10］ HUANG Guangbin，CHEN Lei.Convex incremental extreme learning machine［J］.Neurocomputing，2007，70（16／18）：3056-3062.

［11］ HUANG Guangbin，CHEN Lei.Enhanced random search based incremental extreme learning machine［J］.Neurocomputing，2008，71（16／18）：3460-3468.

［12］ BARRPM A R，COHEN A.Apprpximation and learning by greedy algorithms［J］.Annals of Statistics，2008，36（1）：64-94.