一种级联式多电平逆变器的调制策略

姜凯文，谢 卫，方成辉

（上海海事大学 物流工程学院，上海201306）

0 引 言

多电平逆变器的时代始于20世纪80年代。最早出现的多电平逆变器是由Nabae、Takahashi和Akagi所发明的三电平二极管钳位式逆变器［1］。随后很快就出现了各种带有更多直流电平的二极管钳位式和级联式多电平逆变器的方案［2］。Carrara等人于1992年提出的调制波形和载波波形的布置方案，为各种多电平调制方式的分类做出了重大贡献。在之后的发展中，相继出现了（APOD）PWM、（POD）PWM、（PD）PWM以及混合式多电平逆变器的等效（APOD）PWM、等效（POD）PWM、等效（PD）PWM［3，4］。这些调制方式大都具有复杂的载波波形和开关方式，尤其是在七电平以上的情况下。Young－Min Park等人［5］在2006年，提出一种载波移相的多电平调制方式。作者认为，虽然对载波移相可以构造出多电平的PWM波，但就谐波消除而言，载波移相的方式效果似乎不甚理想。

本文提出一种新的移相级联方式，这种方式不需要复杂的载波波形以及开关控制方式。文中先给出这种移相方式的基本原理，再搭建电路模型，最后用Matlab／Simulink软件进行仿真，得出结果，并分析得出结论。

1 移相PWM的基本原理

对于两个幅值、频率、相位完全相同的正弦波形，如果将其中一个波形相移πrad后，再与另一个未相移的波形进行叠加，结果两个波形被互相抵消了。依据这个基本原理，将电源电路中生成的开关波形进行适当相移后再级联，便可有效消除开关电路所产生的谐波。图1为将要用到的H－bridge。

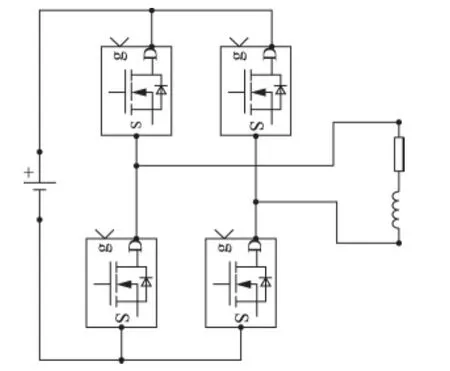
图1 H桥电路

单相桥式双边沿自然采样的开关波形解析表达式如下：

式中，Jn（x）为贝塞尔函数；ω0为参考波角频率；ωc为载波角频率。

使用另一路180°反相桥臂调制得到的开关波形表达式如下：

根据式（1）可知，若将整个开关波形在时间轴上向右移动π／ωcs，再与原波形叠加，则可消除所有奇次载波谐波并且大幅削减相关的边带谐波。而消除偶次载波谐波及其边带情况有所不同，若将整个开关波形在时间轴上向右移动π／2ωcs，再与原波形叠加，只能消除2次载波谐波及其大幅削减相关边带，对其他的偶次谐波及其边带影响甚微。

以消除2次载波谐波为例，整个开关波形需在时间轴上右移π／2ωcs，然后与原波形叠加。此时，2次谐波完全消除，其相关边带谐波将大幅削减。然而，对于基波电压来说，其波形仅仅移动了（πω0／2ωc）rad。一般来说载波频率远远大于参考波频率，以载波比（fc／f0）＝30为例，基波相移仅仅为π／60 rad。因此，这种以消除谐波为目的的相移对基波来说几乎没有影响。

2 电路模型

从上述分析中可以看到，每移相一次，所需的H桥数量将增加一倍，即H桥数量为2N（N为移相次数）。因此这种移相级联的方法适合生成3＋2N个电平的电压。由式（3）可知，两个反相H桥的线电压将不含奇次谐波及其相关边带。因此，H桥级联的目的是削减开关波形中的偶次边带谐波，每移相一次可削减一个偶次载波的边带谐波。以下将给出移相一次得到的五电平电路模型（图2）和移相两次得到的九电平电路模型（图3）。

3 仿真结果及分析

利用 Matlab／Simulink软件进行仿真，取M＝0．9，fc／f0＝30。对于五电平电路，每个 H 桥的Udc＝25 V；对于九电平电路，每个H桥的Udc＝12．5V。

图2 五电平电路

图3 九电平电路

五电平级联移相电路的仿真结果如图4，图5。九电平级联相移电路的仿真结果如图6，图7。

图4 五电平级联移相电路的开关波形

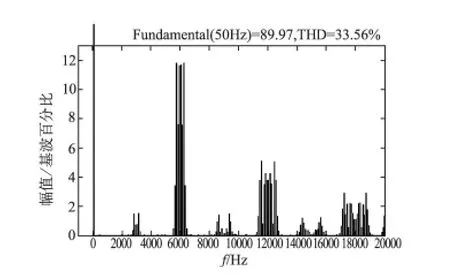
图5 五电平级联移相电路开关波形的FFT

图6 九电平级联移相电路开关波形

图7 九电平级联移相电路的开关波形的FFT

从仿真结果中可以看到，用移相级联的方式构成的五电平电路主要削减的是2次载波边带谐波，九电平电路则在五电平电路的基础上又削减了4次载波边带谐波，因此，用移相级联方式构成的多电平电路谐波状况十分理想（见表，表2）。以九电平电路为例，这种调制方式的THD＝16．90%。虽然在所有九电平调制方式中，THD值不是最低，但是这种调制方式有一个很大的优势，就是谐波主要分布在高频处。以fc／f0＝30为例，谐波成分主要分布在240次谐波附近。事实上这可以看作是一种以消除低频谐波为目的的调制方式。

表1 五电平级联移相电路输出波形的主要谐波（所有谐波都对基波分量进行了标幺化）

表2 九电平级联移相电路输出波形的主要谐波（所有谐波都对基波分量进行了标幺化）

4 结 论

经过电路模型搭建、仿真，可以看到，与众多多电平逆变器的调制方式相比，移相级联调制方式具有非常简单的开关控制方式，而且其谐波方面的表现亦不逊色于其他调制方式，尤其是低频区域谐波分量很少。总的来说，移相级联调制方式是一种比较好的多电平调制方式。

［1］ Nabae A，Takahashi I，Akagi H．A new neutral－pointclamped PWM inverter［J］．IEEE Trans．on Industry Applications，1981，17（5）：518－523．

［2］ Bhagwat P，Stefanovic V R．Generalized structure of a multilevel PWM inverter［J］．IEEE Trans．on Industry Application．1983，19（6）：1057－1069．

［3］ Grahame D，Holmes，Thomas A Lipo．Pulse Width Modulation for Power Converters：Principle and Practice［M］．A John Wiley ＆Sons，2003．

［4］ Corzine K A，Wielebski M W，Peng F Z，Jin Wang．Control of cascaded multilevel inverters［J］．IEEE Transactions on Power Electronics，2004，19（3）：732－738．

［5］ Young－Min Park，Han－Seong Yoo，Hyun－Won Lee，Myung－Gil Jung，Se－Hyun Lee，Choong－Dong Lee，Sang－Bin Lee，Ji－Yoon Yoo．A Simple and Reliable PWM Synchronization ＆ Phase－Shift Method for Cascaded HBridge Multilevel Inverters based on a Standard Serial Communication Protocol［C］．IEEE．Industry Applications Conference，2006．41stIAS Annual Meeting．2006：256－645．