光伏并网系统设计中发电量计算研究

北京科诺伟业科技股份有限公司 ■ 王鸿运 王伟 梁勃

0 引言

随着化石能源的日趋枯竭和人类对能源需求的不断加大，能源问题越来越成为世界各国面临的严峻挑战，人类加快了寻找替代能源的步伐，开发和利用可再生能源(如太阳能、风能等)成为人类社会的迫切需要。与此同时，基于可再生能源的分布式发电系统具有多方面的优点，尤其是光伏发电，与化石能源、核能、风能和生物质能发电技术相比，具有发电原理先进、发电形式简洁、太阳能资源无限分布、环境友好等一系列优势，且采用的模块结构易于建造安装、拆卸迁移，规模大小随意，而且便于随时扩大发电容量。近几年，光伏并网发电开始大规模应用，在未来拥有广阔的市场空间[1]。

太阳能光伏电站通常按照最佳倾角来安装光伏组件。为获得全年最优发电量，光伏组件最佳倾角设计方法至关重要。为最大程度减少固定式安装方式对各月太阳辐照资源不同程度的浪费，需要折衷考虑倾斜面年辐射随倾角变化趋势，以获得全年最优发电量。在光伏电站设计初期，发电量预测对于整个电站经济效益和社会效益的评估具有至关重要的意义，因此如何准确地预估发电量也越来越成为可再生能源发电领域的研究热点之一[2]。

本文利用现有电站已采集的数据和国际通用的分析方法，对大型光伏并网电站设计的技术问题进行研究，简要介绍光伏电站发电量计算的基本思路，并与光伏工程常用仿真软件PVsyst模拟结果及现有电站监测数据进行对比来验证计算思路的正确性。

1 日照资源分析

本项目位于山东半岛西南部即墨市，建设规模 3 MWp，坐标 120°07′～121°23′ E、36°18′～36°37′ N，东临黄海，与日本、韩国隔海相望，南依崂山，近靠青岛。通过NASA网站查得该地区太阳能辐射及环境温度数据见表1。

根据表1可看出，即墨市阳光资源非常丰富，年总辐射量达到1543.88 kWh/m2，年平均气温为12.8 ℃。其日均辐照度曲线图如图1所示。

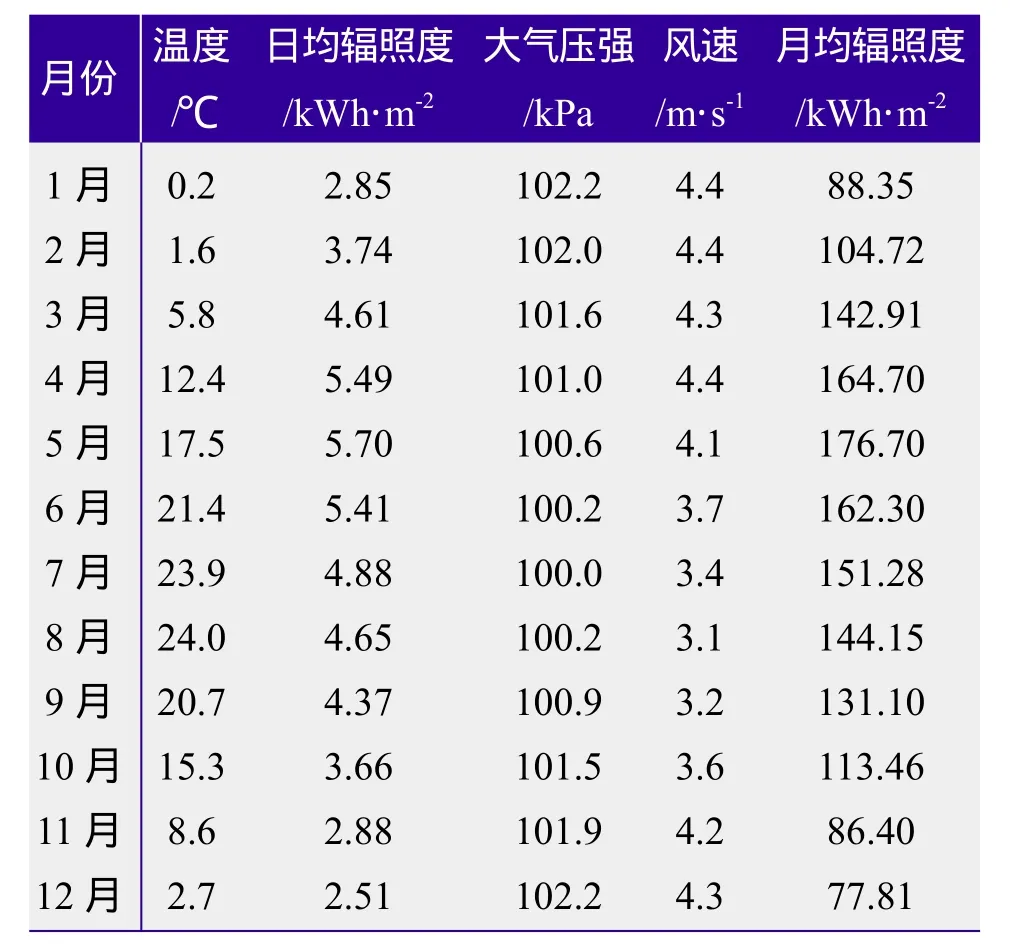
表1 即墨市多年气象及水平总辐射平均值(NASA)

图1 各月日均辐照度曲线图

由图1可看出，即墨市太阳辐照资源主要分布在4～8月份，其他月份较少。

2 光伏组件最佳倾角分析

2.1 倾斜面辐射量理论计算方法

倾斜面总辐射量的计算式如式(1)：

式中，HT为倾斜面总辐射量；HBR为倾斜面直接辐射量；HDR为倾斜面天空散射量；HRT为倾斜面地面反射量。各变量计算式见式(2)～(4)：

式中，Hb为水平面上的直射量；Hd为水平面上天空散射量；H为水平面上辐射总量；ρ为反射系数；Rb为斜面上直射量与水平面上直射量之比；KT为水平面上直接辐射与大气层外水平面太阳辐射之比。

倾斜面上任意时刻计算式为：

反射系数ρ取值可参照表2。

表2 反射系数ρ取值表

Rb和KT的取值为多个统计时段的平均值，根据式(1)～(5)即可得出计算时刻倾斜面辐射量[3, 4]。

2.2 最佳倾角分析

根据表1和2.1所述计算方法，可计算出即墨市不同倾斜角度的平均辐射量，如表3所示。

由表3可看出，在34°倾角时，倾斜面辐射量最大。倾斜表面太阳辐射量折线图如图2所示。

图2 各倾角下倾斜面辐射量

表3 即墨市各倾角的倾斜面平均辐射量

3 发电量计算研究

3.1 光伏发电系统效率分析

光伏发电系统的发电量除了与当地的太阳辐射量、光伏方阵的安装倾角等因素有关，还与光伏发电系统效率密切相关。影响系统效率的因素包括：

1)光伏阵列效率η1。光伏阵列在能量转换与传输过程中的损失包括：光伏阵列在1000 W/m2太阳辐射强度下，实际直流输出功率与标称功率之比。光伏阵列在能源转换过程中的损失包括：组件的匹配损失、表面尘埃遮挡损失、不可利用的太阳辐射损失、温度影响、最大功率点跟踪精度及直流线路损失等。

2)逆变器的转换效率η2。额定情况下逆变器输出的交流功率与直流功率之比。对于本项目所选用的并网型逆变器，可取η2=97%。

3)交流并网的效率η3。从逆变器输出至高压电网的传输效率，其中主要是变压器的效率[5-7]。

综上所述，光伏电站系统效率为：

因光伏项目场地环境的差异性，各损失因素取值有所不同。本项目各损失因素取值可参照表4。

表4 影响光伏系统效率因素取值表

3.2 发电量计算

光伏电站发电量可采用下述公式来进行估算：

式中，L为光伏并网电站年发电量；W为固定式发电单元装机容量；t为倾斜面年峰值日照小时数；η为光伏系统效率。

年峰值日照小时数可由年均水平辐射数据计算得出。由此估算即墨市3 MWp光伏电站的首年各月发电量如表5所示。

表5 即墨市3 MWp光伏电站首年各月发电量

3.3 对比分析

为了验证计算方法的正确性，本文采用光伏电站工程项目设计中的常用软件PVsyst进行仿真模拟。图3为即墨市3 MWp电站的发电量数据PVsyst模拟报告，图4为本文所述方法计算结果，可见两者误差率在10%以内。

图3 即墨市3 MWp电站发电量数据PVsyst模拟报告

图4 即墨市3 MWp电站发电量计算结果

为验证计算方法的真实有效，本文截取了即墨电站监控系统2013年全年发电量数据，与计算结果进行对比，如图5所示。

图5 2013年实测数据与理论计算值对比图

由图5可分析发电量理论计算值与电站实测值之间的偏差率。为清晰反映两者间的偏差，用折线图来表示偏差率，见图6。

图6 理论计算值偏差率

由图6可知，计算结果与实测数据在全年的发展趋势一致，但1～5月和12月的理论值高于实测值2%～8%，6～11月却比实测值稍低。其原因主要有：

1)山东即墨地区春冬季节气温较低，气候干燥降水较少，而夏秋季节降水较多。实际计算时选取的温度和降水影响因素系数源于NASA多年平均值，与某一年实测值之间存在偏差。

2)理论计算时选取的影响光伏系统效率因素均为恒定值，实际上表面尘埃遮挡损失、不可利用太阳辐射损失等因素均为变量；且地面反射系数会随着地表植被、降水等原因而相应变化，对组件倾斜表面辐射量有一定的影响。

4 结论

本文的发电量计算方法简便易行，能估算出光伏电站发电量的发展趋势和数值，与光伏设计软件PVsyst仿真结果相一致，且通过与实际监测发电量数值相比较偏差率在10%以内，验证了计算方法的可行性和准确性，可为光伏设计人员提供参考。

[1] 郑志杰， 李磊， 王葵. 大规模光伏并网点站接入系统若干问题探讨[J]. 电网与清洁能源, 2010, 26(2): 74－76.

[2] 马金玉, 罗勇, 申彦波, 等. 太阳能预报方法及其应用和问题[J]. 资源科学, 2011, 33(5): 829－837.

[3] [日]太阳光发电协会[编], 刘树民, 宏伟译[译]. 太阳能光伏发电系统的设计与施工[M]. 北京: 科学出版社, 2006.

[4] Martin L, Zarzalejo J F, Polo J, et al. Prediction of global solar irradiance based on time series analysis: Application to solar thermal power plants energy production planning[J]. Solar Energy,2010, 84(10): 1772－1781.

[5] Voyant C, Muselli M, Paoli C, et al. Predictability of PV power grid performance on insular sites without weather stations: use of artificial neural networks[A]. 24th European Photovoltaic Solar Energy Conference[C], EUPVSEC, 2009.

[6] Duffi e J A, Backman W A. Solar engineering of thermal processes[M]. NewYork: John Wiley & Sons. INC, 1991, 113－119.

[7] 杨金焕, 黄晓橹， 陆钧. 一种独立光伏系统设计的新方法[J].太阳能学报, 1995, 16(4): 407－414.