基于Matlab/GUI的钻机动力头齿轮动态优化设计

罗 华

(1．中煤科工集团重庆研究院有限公司，重庆400039;2．瓦斯灾害监控与应急技术国家重点实验室，重庆400037)

0 引言

动力头作为全液压钻机的动力输出机构，采用液压驱动和齿轮传动相结合的方式，主要由液压马达、齿轮减速箱和钻杆夹持装置3部分组成［1］。ZYWL－2600R型钻机动力头的结构如图1所示，其设计传递功率为49 kW，输出转速180～900 r/min，最高输出扭矩2600 N·m。其中，齿轮减速箱部分采用单级斜齿轮传动，是动力头设计的关键部分。随着该钻机输出转速和功率的增加，振动和噪声问题变得越来越突出，使得动态特性成为了设计中必须考虑的技术要求。

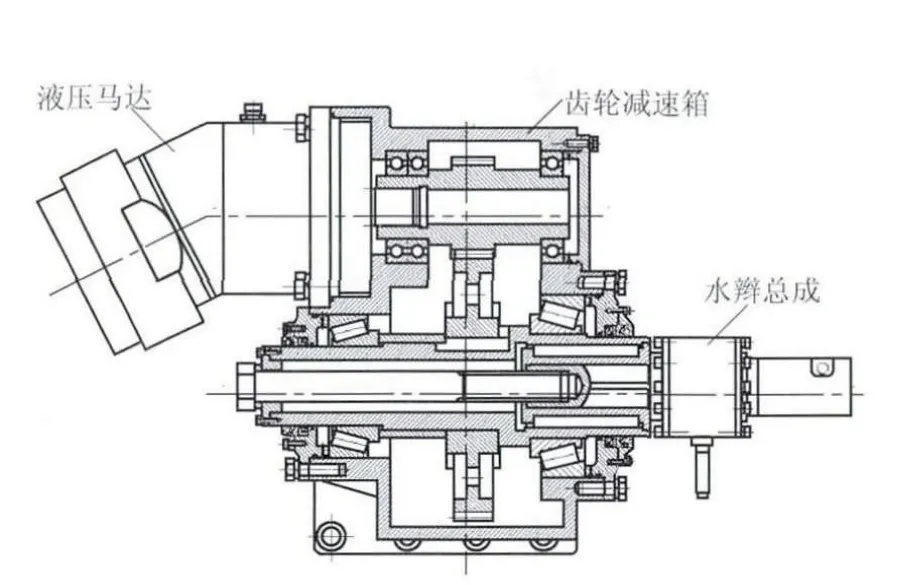
图1 ZYWL－2600R型钻机动力头结构

为了设计出具有良好的动态特性钻机动力头，传统的静态优化设计已不能满足要求。因此，本文以齿轮系统动力学为基础，建立动力头传动齿轮的动态优化设计模型，借助Matlab优化工具箱和GUI工具开发了齿轮动态优化设计程序的图形界面，求解以齿轮振动加速度最小为优化目标的齿轮设计参数，通过计算结果对比验证了程序的有效性和实用性。

1 齿轮动态优化设计模型的建立

本文以传动齿轮副为研究对象，为简化计算，在分析时，假设箱体为不发生变形的刚体支撑，同时在不考虑传动轴和支撑轴承的弹性变形。

1．1 设计变量

影响斜齿轮动态特性的参数比较多，考虑到设计需求和动态优化设计的迭代计算量较大，只选取齿轮的基本设计参数为设计变量，包括主、从动齿轮齿数z1和z2、法面模数mn、齿宽 b、螺旋角β和法面变位系数xn1和xn2共7个参数，即:

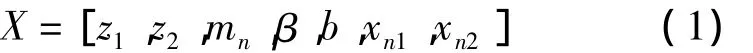
1．2 目标函数

1．2．1 齿轮动力学方程

根据钻机动力头齿轮的传动啮合特性，考虑了齿轮副时变综合啮合刚度、啮合阻尼及传动误差，建立齿轮副的扭转振动模型如图2所示，相应的动力学方程为［2－3］:

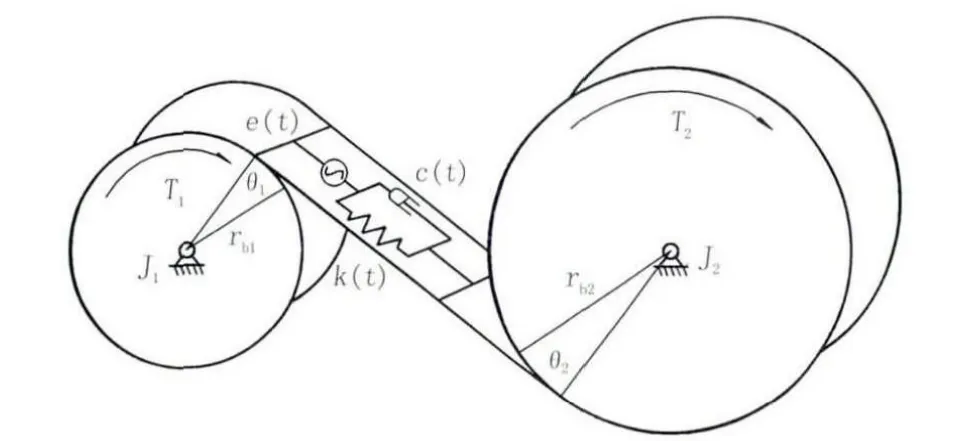
图2 动力头斜齿轮副的扭转振动模型

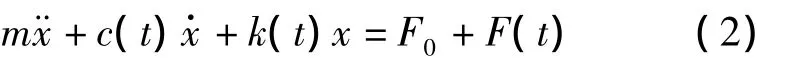
式中:x——啮合线方向上的相对位移;m——齿轮的当量质量，齿轮副之间的静态载荷，F0=T1/rb1=T2/rb2;F(t)——其动态啮合力，F(t)=Δk(t)·e(t);其中，θi、Ji和 rbi——分别为齿轮实际回转角、转动惯量和基圆半径(i=1，2)，k(t)——齿轮副的时变综合啮合刚度，c(t)——齿轮副的啮合阻尼，e(t)——齿轮副沿啮合线方向的传动误差。

1．2．2 动态优化目标

齿轮的振动噪声与振动加速度的均方根值成正比，反映了齿轮传动系统的振动程度［3］。因此，本文选用啮合线上振动加速度的均方根值作为动力头齿轮优化设计的目标函数。其计算式为:

1．2．3 相关参数的计算

(1)齿轮副啮合刚度k(t)。

对于理想精度的斜齿轮副，为简化计算，常用齿轮副接触线长度的变化代替齿轮副啮合刚度的变化，仍具有良好的计算精度［4－5］。求解时，将单位接触线长度上的啮合刚度Cγ与齿轮副瞬时接触线总长度L(τ)相乘，得到齿轮副时变啮合刚度:

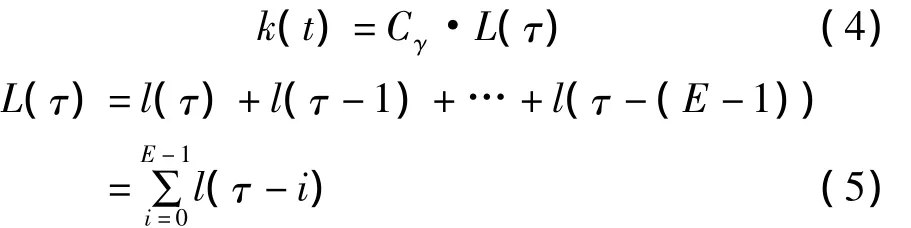
式中:τ=t/Tz，Tz——齿轮副的啮合周期;E——同时参与啮合的最大齿对数;l(τ)——单对齿啮合的接触线长度函数，周期为E，按傅里叶级数展开得:

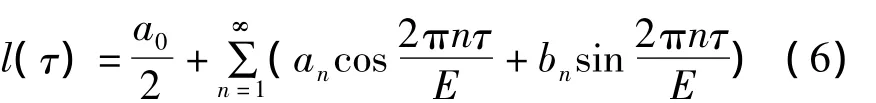
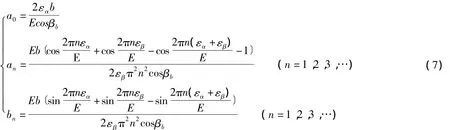
式中:εα——端面重合度;εβ——轴向重合度;βb——基圆螺旋角。

(2)齿轮副的啮合阻尼c(t)。

啮合阻尼c(t)可按经验计算公式计算［6］:

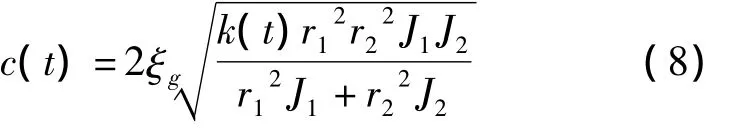
式中:ξg——轮齿啮合阻尼比，根据文献［6］的分析

计算，一般取0.03～0.17。

(3)传动误差e(t)。

由于齿轮的制造、安装和轮齿受载变形等引起的啮合轮廓偏离理论的理想位置，产生传动误差激励。在设计时，本文只考虑齿轮的精度等级引起的齿轮位置偏差，采用齿轮啮合频率的简谐函数来模拟传动误差:

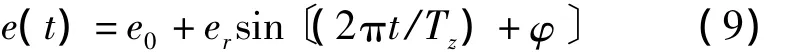
式中:e0——齿轮副传动误差的常值，由基节误差和齿形误差按正态分布合成;er——齿轮副传动误差的幅值。

1．3 约束条件

齿轮传动系统动态优化设计中，约束条件主要包括设计变量取值范围的边界约束、齿轮静态性能的约束函数和动态性能约束三种。其中，静态性能约束主要包括齿轮不产生根切的最小齿数、齿顶厚度的限制条件、重合度的限制条件、不发生过渡曲线干涉的条件、齿面接触强度条件、齿根弯曲强度条件等。动态性能约束有最大动载荷、动载系数、最大振动加速度等动态特性参数。

按照钻机动力头的设计经验，齿轮副的设计既要保证传动系统的承载能力还要使结构紧凑，一般取模数的约束范围:

为了保证传动的平稳性，可以采取增加螺旋角的措施，但轴向力也会随之增大。因此，螺旋角的选取一般取:

对于变位齿轮传动，端面重合度会随着啮合角的增大而减小，为了保证一定的重合度，需限制重合度的取值为:

其它各约束条件的计算和取值范围参考机械设计手册［7］的推荐和要求，在此不在赘述。

2 优化设计的求解与GUI开发

2．1 Matlab优化工具箱

实际的机械优化设计问题大都属于非线性规划，其数学模型可以表示为:

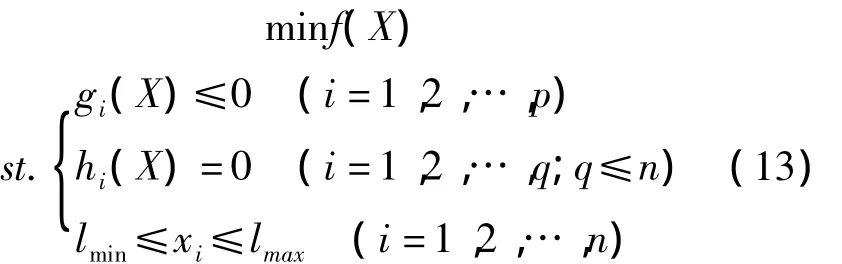
式中:X——设计变量;f(X)——目标函数;gi(X)≤0，hi(X)=0为约束条件。

Matlab软件为解决这种问题提供了相应的工具包，利用工具箱中的相关函数，可以求解线性规划、非线性规划和多目标规划等问题，为优化设计提供了更高效快捷的求解方法。

齿轮副的动态优化设计属于式(13)所描述的多变量约束最小值优化问题，因此可以采用局域优化指令fmincon进行求解。

2．2 GUI的设计与开发

图形用户界面(Graphical User Interfaces，GUI)为程序的实现提供了一个生动、友好的操作环境，用户通过鼠标或键盘的选择激活这些图形对象，实现计算、绘制图表和产生动画等［8－9］。

通过使用Matlab/GUI开发工具，设计程序的图形界面如图3和图4所示。

该程序由齿轮参数的静态计算、齿轮振动的动态响应和优化程序3部分组成。程序的输入参数主要是齿轮设计参数、载荷(动力头输出转速、扭矩)、齿轮材料值(弹性模量、泊松比、材料疲劳极限强度)和齿轮精度等级参数(齿形偏差、基节偏差)等;静态计算可以实现齿轮几何参数的计算和疲劳强度校核;动态响应程序可以绘制齿轮的振动位移、速度和加速度响应曲线;最后调用优化程序完成齿轮副的动态优化设计，得到满足要求的齿轮设计参数。

在进行优化设计时，程序会调用输入的齿轮设计参数，计算目标函数值。然后点选约束条件中的所有选项，点击“开始优化”按钮，优化计算的时间与设计变量的初始值、约束条件和求解动态方程的难易有关。计算结束后，点击“圆整结果”按钮，程序会按照标准选取模数，对其它参数进行圆整，点击“复制结果”按钮，可将优化结果传递到齿轮设计参数中，重新进行静态和动态参数的计算。

3 动态优化设计结果与分析

动力头齿轮的设计参数:z1=23，z2=65，mn=5、b=50、β =12°。其中，小齿轮的材料为 42CrMo，大齿轮的材料选用20CrMnTi。

通过动态优化设计程序求解后，得到优化前后的齿轮静态性能参数如表1所示。

图3 齿轮动态优化设计程序图形界面Ⅰ

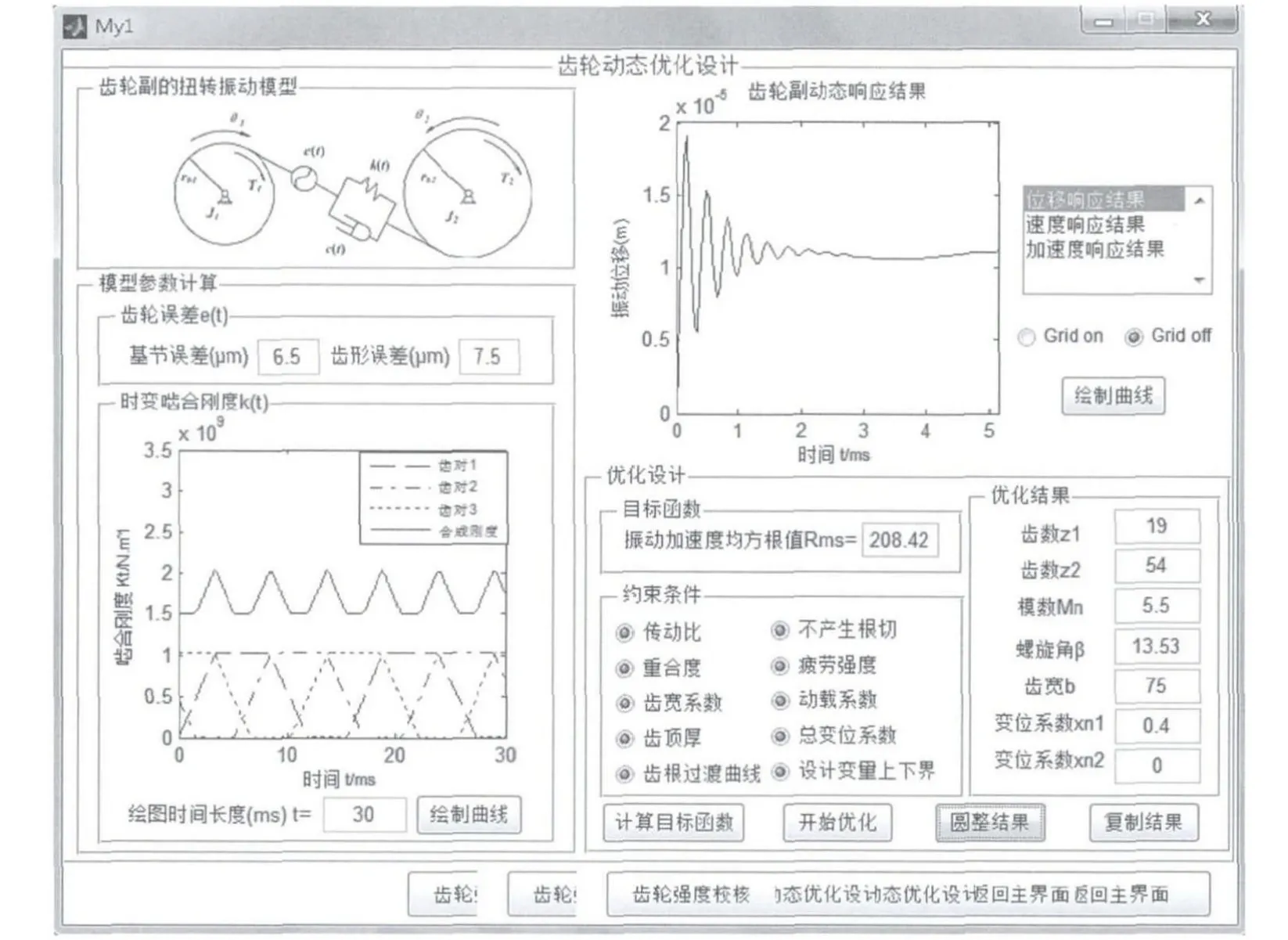
图4 齿轮动态优化设计程序图形界面Ⅱ

从表1中的数据可以看出:优化后齿轮振动加速度的均方根值减小了32.8%，有效降低了齿轮传动的振动;而且，齿轮副的接触和弯曲疲劳强度均有较大提高，采用变位齿轮转动后的大、小齿轮的弯曲疲劳强度趋于一致。

表1 齿轮动态优化设计参数

优化前后的齿轮副时变啮合刚度曲线和振动加速度响应曲线分别如图5、图6所示。

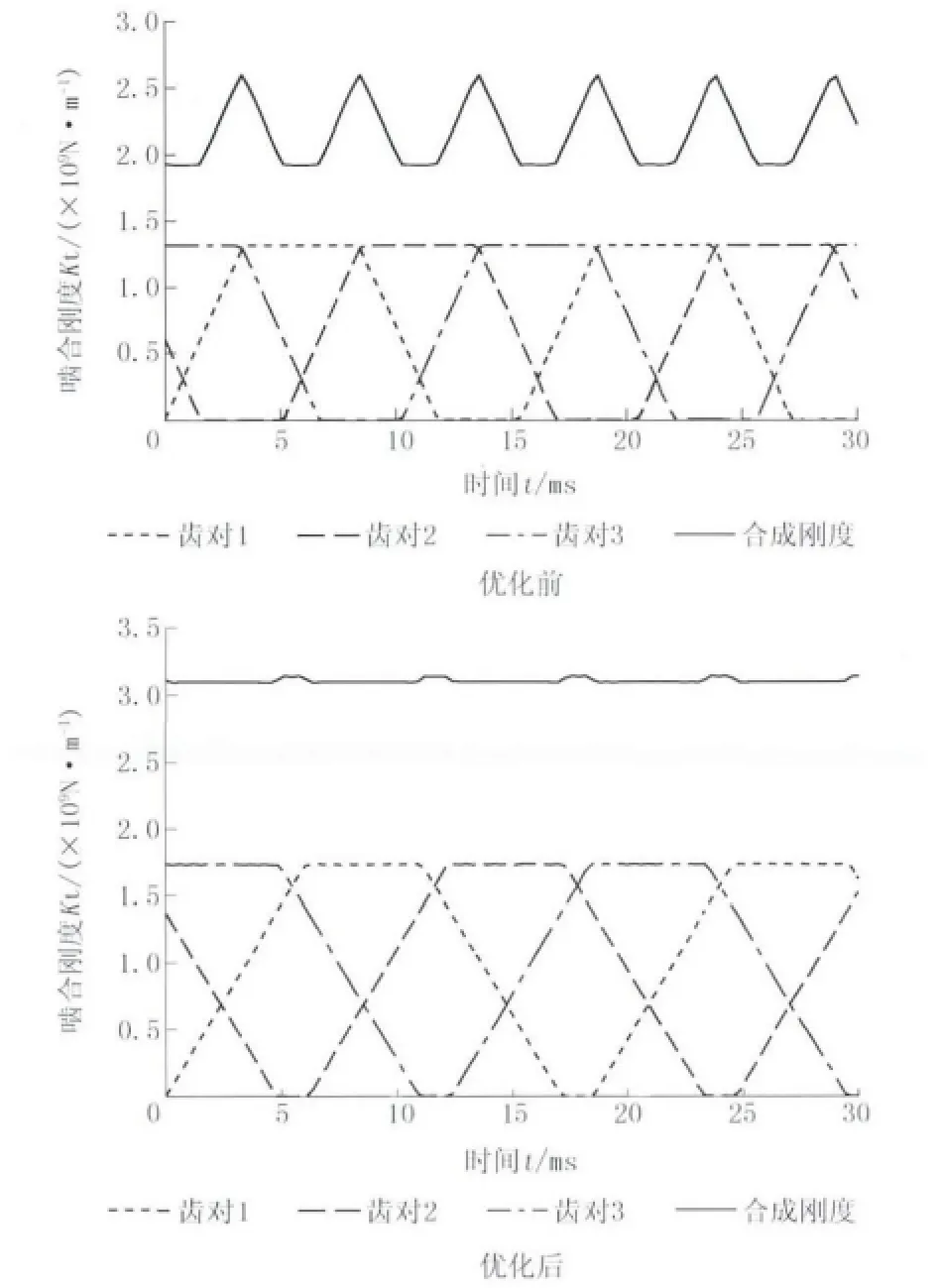
图5 优化前后的齿轮副时变啮合刚度曲线

优化后齿轮副的啮合刚度曲线较为平滑，只有微小的刚度变化，没有较大的突变和“尖点”，大大降低了轮齿啮合的刚度激励，明显地缩短了齿轮啮合过程中的振动时间，使啮合过程更快地进入平稳传动状态。

4 结语

本文建立了钻机动力头齿轮副的动态优化设计模型，借助Matlab/GUI工具设计了优化程序的图形界面，通过实例计算和对比验证了程序的可行性和结果的合理性，有效降低了齿轮副的振动，为设计具有良好动态特性的动力头齿轮传动提供了有力的工具。

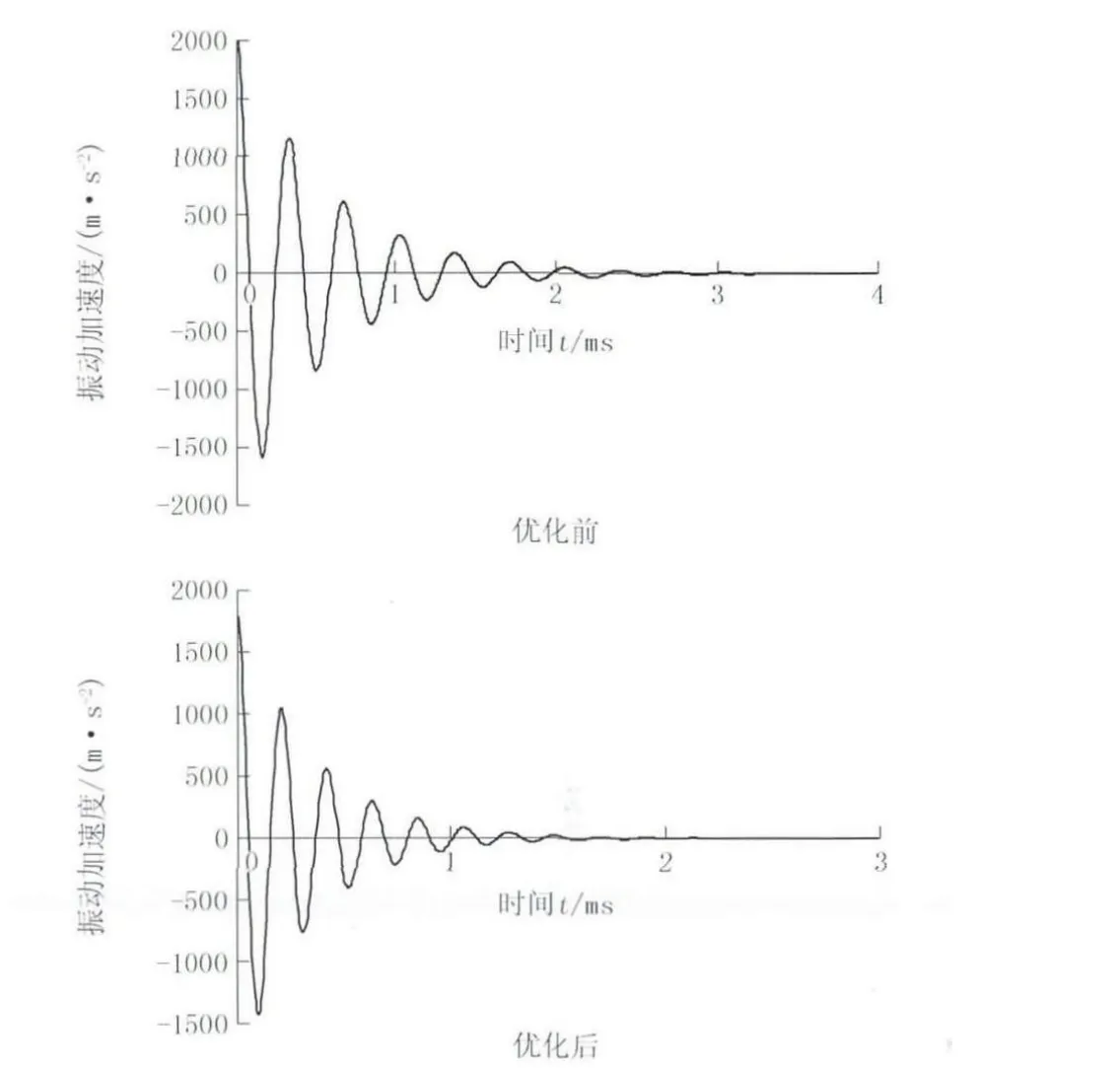
图6 优化前后的振动加速度响应曲线(一个啮合周期)

［1］ 吕冰，王清峰，史春宝．ZY－6000煤矿用全液压坑道钻机动力头设计［J］．矿业安全与环保，2007，34(2):29 －30．

［2］ 马亮，杨电科．一种舰船用齿轮传动的动态优化设计方法［J］．机械传动，2002，26(2):39 －41．

［3］ 杜雪松，朱才朝，宁杰．船用齿轮传动的动态优化设计［J］．重庆大学学报，2011，34(5):14 －18．

［4］ 李润方，陶泽光，林腾蛟，等．齿轮啮合内部动态激励数值模拟［J］．机械传动，2001，25(2):1 －3．

［5］ C－C Zhu，B Lu，C－S Song and D－T Qin．Dynamic analysis of a heavy duty marine gearbox with gear mesh coupling［J］．Proceedings of the Institution of Mechanical Engineers，Part C:Journal of Mechanical Engineering Science 2009，223:2531．

［6］ 李润方，王建军．齿轮系统动力学——振动、冲击、噪声［M］．北京:科学出版社，1997．

［7］ 成大先．机械设计手册．第3卷(第五版)［M］．北京:化学工业出版社，2008．

［8］ 陈垚光．精通MATLAB GUI设计(第二版)［M］．北京:电子工业出版社，2011．

［9］ 陈欠根，李琳，郝鹏．利用MATLAB/GUI的挖掘机动力系统散热模型仿真研究［J］．现代制造工程，2009，(5):71－74．